苏教版六年级下学期数学4.2比例的基本性质课件(共19张PPT)
文档属性
| 名称 | 苏教版六年级下学期数学4.2比例的基本性质课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 31.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-15 16:10:23 | ||
图片预览




文档简介
(共19张PPT)
比例的基本性质
学习目标
通过自主学习,让学生经历探究的过程,体验成功的快乐。
使学生认识比例的“项”以及“内项”和“外项”。
重难点
重点:理解并掌握比例的基本性质。
难点:运用比例的基本性质判断两个比能否组成比例, 并能正确地组成比例。
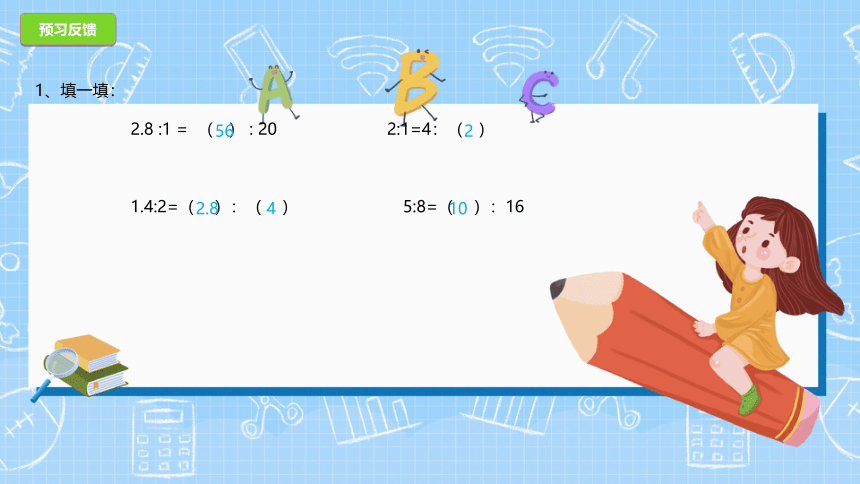
预习反馈
1、填一填:
2.8 :1 = ( ) : 20 2:1=4:( )
1.4:2=( ):( ) 5:8=( ):16
56 2
2.8 4 10
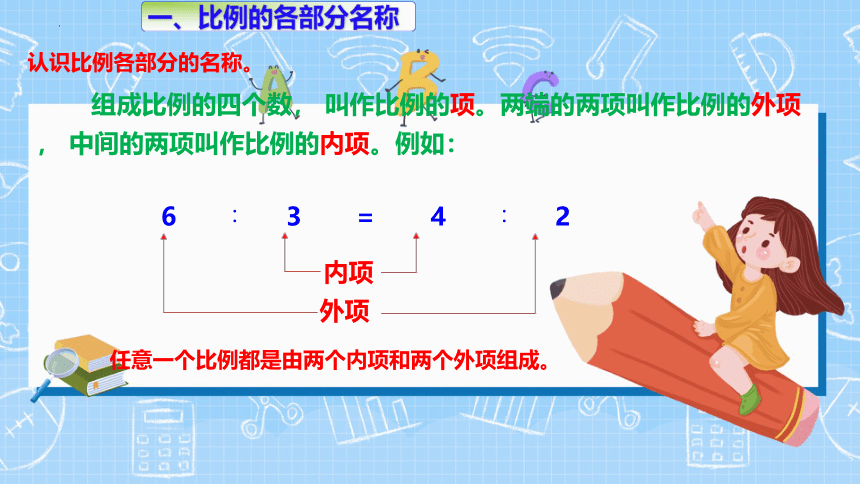
一、比例的各部分名称
认识比例各部分的名称。
组成比例的四个数, 叫作比例的项。两端的两项叫作比例的外项, 中间的两项叫作比例的内项。例如:
6 ∶ 3 = 4 ∶ 2
外项
内项
任意一个比例都是由两个内项和两个外项组成。
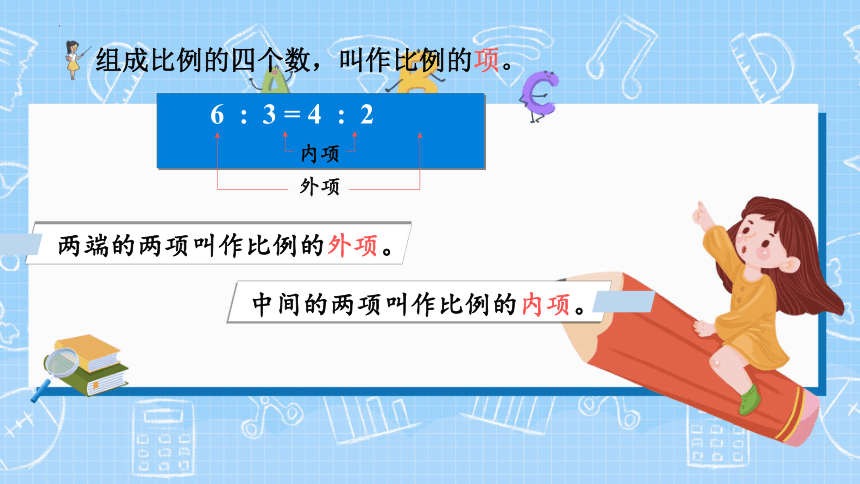
6 : 3 = 4 : 2
两端的两项叫作比例的外项。
中间的两项叫作比例的内项。
外项
组成比例的四个数,叫作比例的项。
内项
讲授新课
6 :3 = 4 :2
4 :2 = 6 :3
两个三角形底的比
和高的比相等。
两个三角形高的比
和底的比相等。
课堂探究
如果把比例写出分数形式,把等号两端的分子、分母交叉相乘,结果怎样?
探究:
把比例写出分数形式,把等号两端的分子、分母交叉相乘,结果相等。
6×2=3×4
在比例里,两个外项的积等于两个内项的积,这叫作比例的基本性质。
如果用字母表示比例的四个项,a∶b = c∶d,那么这个规律可以怎样表示
a×d = b ×c
运用比例的基本性质判断两个比能否组成比例,就看一个比的前项与另一个比的后项乘积是否等于这个比的后项现另一个比的前项的乘积,如果相等,那么这两个比能组成比例。
讲授新课
如果把比例写成分数形式,把等号两端的分子、分母交叉相乘,结果怎样?
6×2=3×4
为什么交叉相乘的积相等?
如果把比例写成分数形式,把等号两端的分子、分母交叉相乘,结果怎样?
6:3=4:2
4:2=6:3
6:4=3:2
4:6=2:3
随堂检测
下面哪几组中的四个数可以组成比例?把组成的比例写出来。
(1)5,7,15和21 (2)2,4,6和8
(3) (4)
能, 5:15=7:21 不能
能, 能,
2、在比例3∶12 = 6∶24中,如果将第一个比的前项加6,那么第二个比的前项应( )比例才能成立。
乘3或加12
(3+6)×24=216
216÷12=18
18÷6=3
18-6=12
(教科书第39页练一练)
1. 一列火车从甲城开往乙城,行驶速度和所需时间如
下表:
(1)从表中选择两组数据,写出一个乘积相等的式子。
速度/(千米/时) 80 120 160
时间/时 6 4 3
答案不唯一。如:80×6=120×4。
(2)根据上面的等式,写出一个比例。
答案不唯一。如:80:120=4:6。
当堂练习
判断。
(1)在比例中,两个外项的积减去两个内项的积,差是0。( )
(2)18:30和6:10可以组成比例。( )
(3)如果6X=4Y,(X和Y均不为0),那么6:X=4:Y。 ( )
(4)因为2×10=5×6,所以2:5=10:6。( )
√
√
×
×
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
聪明出于勤奋,天才在于积累。
比例的基本性质
学习目标
通过自主学习,让学生经历探究的过程,体验成功的快乐。
使学生认识比例的“项”以及“内项”和“外项”。
重难点
重点:理解并掌握比例的基本性质。
难点:运用比例的基本性质判断两个比能否组成比例, 并能正确地组成比例。
预习反馈
1、填一填:
2.8 :1 = ( ) : 20 2:1=4:( )
1.4:2=( ):( ) 5:8=( ):16
56 2
2.8 4 10
一、比例的各部分名称
认识比例各部分的名称。
组成比例的四个数, 叫作比例的项。两端的两项叫作比例的外项, 中间的两项叫作比例的内项。例如:
6 ∶ 3 = 4 ∶ 2
外项
内项
任意一个比例都是由两个内项和两个外项组成。
6 : 3 = 4 : 2
两端的两项叫作比例的外项。
中间的两项叫作比例的内项。
外项
组成比例的四个数,叫作比例的项。
内项
讲授新课
6 :3 = 4 :2
4 :2 = 6 :3
两个三角形底的比
和高的比相等。
两个三角形高的比
和底的比相等。
课堂探究
如果把比例写出分数形式,把等号两端的分子、分母交叉相乘,结果怎样?
探究:
把比例写出分数形式,把等号两端的分子、分母交叉相乘,结果相等。
6×2=3×4
在比例里,两个外项的积等于两个内项的积,这叫作比例的基本性质。
如果用字母表示比例的四个项,a∶b = c∶d,那么这个规律可以怎样表示
a×d = b ×c
运用比例的基本性质判断两个比能否组成比例,就看一个比的前项与另一个比的后项乘积是否等于这个比的后项现另一个比的前项的乘积,如果相等,那么这两个比能组成比例。
讲授新课
如果把比例写成分数形式,把等号两端的分子、分母交叉相乘,结果怎样?
6×2=3×4
为什么交叉相乘的积相等?
如果把比例写成分数形式,把等号两端的分子、分母交叉相乘,结果怎样?
6:3=4:2
4:2=6:3
6:4=3:2
4:6=2:3
随堂检测
下面哪几组中的四个数可以组成比例?把组成的比例写出来。
(1)5,7,15和21 (2)2,4,6和8
(3) (4)
能, 5:15=7:21 不能
能, 能,
2、在比例3∶12 = 6∶24中,如果将第一个比的前项加6,那么第二个比的前项应( )比例才能成立。
乘3或加12
(3+6)×24=216
216÷12=18
18÷6=3
18-6=12
(教科书第39页练一练)
1. 一列火车从甲城开往乙城,行驶速度和所需时间如
下表:
(1)从表中选择两组数据,写出一个乘积相等的式子。
速度/(千米/时) 80 120 160
时间/时 6 4 3
答案不唯一。如:80×6=120×4。
(2)根据上面的等式,写出一个比例。
答案不唯一。如:80:120=4:6。
当堂练习
判断。
(1)在比例中,两个外项的积减去两个内项的积,差是0。( )
(2)18:30和6:10可以组成比例。( )
(3)如果6X=4Y,(X和Y均不为0),那么6:X=4:Y。 ( )
(4)因为2×10=5×6,所以2:5=10:6。( )
√
√
×
×
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
聪明出于勤奋,天才在于积累。
