北师大版七年级下册 3.1用表格表示的变量间关系课件(共28张PPT)
文档属性
| 名称 | 北师大版七年级下册 3.1用表格表示的变量间关系课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-16 00:00:00 | ||
图片预览








文档简介
(共28张PPT)
第三章变量之间的关系
3.1用表格表示变量间的关系
回顾与思考
多年前的小男孩
变成了
回顾与思考
如今的巨星
回顾与思考
世界万物都在悄悄地发生着变化,包括温度、时间,人的身高、体重、容颜... ... 如果从数学的角度研究它们之间的关系,将有助于我们更好地认识世界,预测未来。
学习目标
1、在具体情境中理解什么是变量、自变量、因变量。
2、能从表格中获得变量之间关系的信息,能用表格表示变量之间的关系,尝试对变化趋势进行初步的预测。
探究篇
探究篇
探究篇
探究篇
(2)如果用h(厘米)表示支撑物高度,t(秒)表示小车下滑时间,随着h逐渐变大,t的变化趋势是什么?
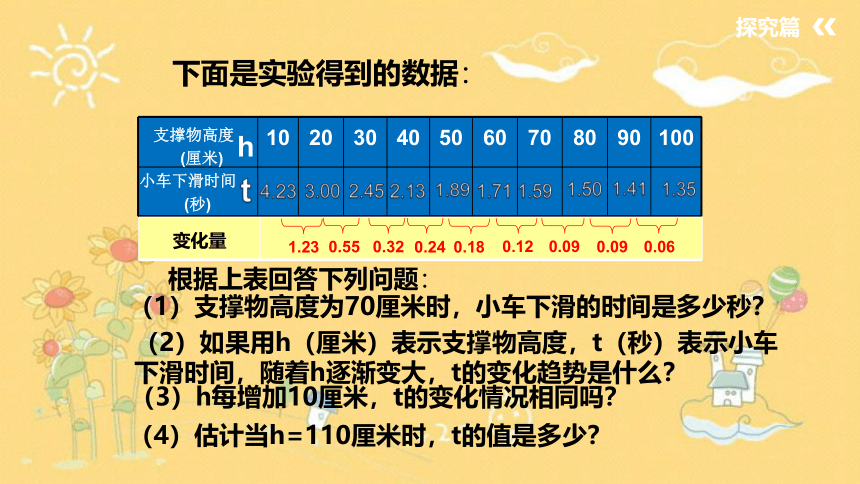
下面是实验得到的数据:
10 20 30 40 50 60 70 80 90 100
(1)支撑物高度为70厘米时,小车下滑的时间是多少秒?
(3)h每增加10厘米,t的变化情况相同吗?
(4)估计当h=110厘米时,t的值是多少?
4.23
1.35
1.41
1.50
1.59
1.71
1.89
2.13
2.45
3.00
根据上表回答下列问题:
支撑物高度
(厘米)
小车下滑时间
(秒)
h
t
变化量
0.55
0.32
0.24
0.18
0.12
0.09
1.23
0.06
0.09
认知篇
认知篇
在《小车下滑的时间》实验中:
支撑物的高度h、小车下滑的时间t、木板的长度,这些量哪些量发生了变化,哪些量始终没有变化?
支撑物的高度h和小车下滑的时间t都在变化,把它们叫做变量.
木板长度一直没有变化.像这种在变化过程中始终不变的量叫常量.
认知篇
在《小车下滑的时间》 中:
在支撑物的高度h和小车下滑的时间t这两个变量中, 随着
的变化而变化?
支撑物的高度h是自变量 。
小车下滑的时间t是因变量 。
认知篇
解析
变 量
自变量
因变量
主动变化的量
被动变化的量
量
常量
表格可以直观地表示因变量随自变量变化而变化的情况,还能帮助我们对变化趋势进行初步的预测。但它也有自己的局限性,你知道是什么吗?
由于变量对应的数值有限,不能全面反映变量间的关系。
认知篇
比比谁更快
(3)婴儿在6个月,1周岁,2周岁时的体重分别大约是出生时的2倍,3倍,4倍.
自变量:时间 因变量:剩余油量
自变量:时间 因变量:水的温度
自变量:年龄 因变量:体重
指出下列实例中自变量与因变量
(1)随着时间推移,汽车在行驶中的剩余油量减少。
(2)烧一壶水,发现在一定时间内温度随时间的
变化而变化,即随时间的增加,温度逐渐增高.
要求:抢答.
认知篇
比比谁更快
改革开放30多年以来,中国人民生活实现了从温饱到小康的历史性的跨越,也就是说人民生活水平的质量逐年提高.在这个过程中,因变量是( )
A.经济发展 B.生活水平质量
C.时间 D.人民
要求:抢答.
B
认知篇
生活中还有哪些例子反映了
变量之间的关系呢?
其中谁是自变量?
谁是因变量呢?
七嘴八舌
知识巩固篇
知识巩固篇
1.某河受暴雨袭击,某天此河水的水位记录为下表:
时间/小时 0 4 8 12 16 20 24
水位/米 2 2.5 3 4 5 6 8
(1)上表中反映了哪两个变量之间的关系?
自变量和因变量各是什么?
(2)12时,水位是多少?
(3)哪一时段水位上升最快?
自变量:时间 因变量:水位
4米
20到24小时
比比谁更快
要求:抢答.
知识巩固篇
研究表明,土豆的产量与氮肥的施用量有如下关系:
(1)上表反映了哪两个变量之间的关系?
是自变量, 是因变量.
(3)根据表格,你认为氮肥的施用量是 时
比较适宜?说说你的理由。
(4)粗略说一说氮肥的施用量对土豆产量的影响。
氮肥施用量 千克/公顷 0 34 67 101 135 202 256 336 404 471
土豆产量 吨/公顷 15.18 21.36 25.72 32.29 34.03 39.45 43.25 43.46 40.83 30.75
氮肥施用量
(2)当氮肥的施用量是101千克/公顷时,土豆的产量
是 ,如果不施氮肥呢?
32.29吨 /公顷
土豆产量
要求:先独立思考后举手回答.
知识巩固篇
用弹簧做挂重物实验,每增加100g,弹簧长度增加1cm,实验数据如下表:
质量(g) 100 200 300 400
长度(cm) 11 12 13 14
(1)在这个实验中,物体的质量是_______量,弹簧
的长度是________量;
自变
因变
(2) 请你预测所挂物体质量为800g时,弹簧总长度是_______若弹簧总长度为15厘米时,所挂物体的质量是________;
(3)不挂物体时弹簧的长度是________ 。
18厘米
500g
10厘米
要求:先组内讨论后举手回答.
知识巩固篇
测量弹簧秤挂重物后的长度
我们在弹簧秤上不断地加上砝码,研究砝码个数
与弹簧长度之间的变化情况,并记录在下表:
砝码个数 1 2 3
读数 5 10 15
问题:若砝码个数为4个,弹簧秤上的读数
会是多少呢?
若10个呢?
n个呢?
实 验
知识巩固篇
(1)上述变化中自变量是 ,因变量是 。
(2)第5排有 个座位,第6排有 个座位。
(3)第n排有 个 座位。
排数
万达电影院地面一部分是扇形,座位按下列方式设置:
座位数
76
80
(56+4n)
排数 1 2 3 4
座位数 60 64 68 72
…… n
……
生活链接接篇
生活链接篇
夏天房中的温度高达40.9℃,现打开空调降温,室内
的温度与空调打开的时间有如下关系:
时间/分 0 2 4 6 8 10 12 14 16 18
温度/℃ 40.9 39.6 38.3 37 35.7 34.4 33.1 31.8 30.5 29.2
①上表反映了哪两变量之间的关系?
自变量和因变量各是什么?
②如果用t表示时间、T表示温度,那么随着t的变化T的变化
趋势是什么?
③若要使温度降到24℃,估计还需多少分钟?
生活链接篇
在某地,人们发现某种蟋蟀叫的次数与温度之间有如下的近似关系:记录蟋蟀每分钟叫的次数,用这个数除以7,然后再加上3就得到当时的温度.小刚同学在不同时间记录了蟋蟀每分钟叫的次数,分别是98次,105次,119次,133次,154次,请你帮助小刚计算出当时的温度,并用表格将它们之间的关系反映出来,并指出上述关系中的自变量和因变量.
生活链接篇
蟋蟀每分钟叫的次数 98 105 119 133 154
当时的温度
17
18
20
22
25
问题:请你描述一下蟋蟀每分钟叫的次数与当时的温度有怎样的关系?
蟋蟀每分钟叫的次数÷7+3=当时的温度.
当堂检测
小红帮助妈妈预算家庭4月份电费开支情况,下表是小红家4 月份连续8天早晨电表显示的读数:
(1)表中反映的自变量是 ,因变量是 ;
(2)估计小红家4 月份每天用电量是 度;
(3)若每度电的电费是0.6元,估计她家4 月份(按30天算)应交的电费是____元.
日期 1 2 3 4 5 6 7 8
电表读数(度) 21 24 28 33 39 42 46 49
日期
电表读数
4
72
知识小结
通过今天的学习,用你自己的话说说你的收获和体会
1.在具体情境中准确找到自变量、因变量以及常量。
2.能从表格中获得变量之间关系的信息,
能用表格表示变量之间的关系,
尝试对变化趋势进行初步的预测。
3.能发现生活中的变量,体会数学中的变量对生活的实际价值。
第三章变量之间的关系
3.1用表格表示变量间的关系
回顾与思考
多年前的小男孩
变成了
回顾与思考
如今的巨星
回顾与思考
世界万物都在悄悄地发生着变化,包括温度、时间,人的身高、体重、容颜... ... 如果从数学的角度研究它们之间的关系,将有助于我们更好地认识世界,预测未来。
学习目标
1、在具体情境中理解什么是变量、自变量、因变量。
2、能从表格中获得变量之间关系的信息,能用表格表示变量之间的关系,尝试对变化趋势进行初步的预测。
探究篇
探究篇
探究篇
探究篇
(2)如果用h(厘米)表示支撑物高度,t(秒)表示小车下滑时间,随着h逐渐变大,t的变化趋势是什么?
下面是实验得到的数据:
10 20 30 40 50 60 70 80 90 100
(1)支撑物高度为70厘米时,小车下滑的时间是多少秒?
(3)h每增加10厘米,t的变化情况相同吗?
(4)估计当h=110厘米时,t的值是多少?
4.23
1.35
1.41
1.50
1.59
1.71
1.89
2.13
2.45
3.00
根据上表回答下列问题:
支撑物高度
(厘米)
小车下滑时间
(秒)
h
t
变化量
0.55
0.32
0.24
0.18
0.12
0.09
1.23
0.06
0.09
认知篇
认知篇
在《小车下滑的时间》实验中:
支撑物的高度h、小车下滑的时间t、木板的长度,这些量哪些量发生了变化,哪些量始终没有变化?
支撑物的高度h和小车下滑的时间t都在变化,把它们叫做变量.
木板长度一直没有变化.像这种在变化过程中始终不变的量叫常量.
认知篇
在《小车下滑的时间》 中:
在支撑物的高度h和小车下滑的时间t这两个变量中, 随着
的变化而变化?
支撑物的高度h是自变量 。
小车下滑的时间t是因变量 。
认知篇
解析
变 量
自变量
因变量
主动变化的量
被动变化的量
量
常量
表格可以直观地表示因变量随自变量变化而变化的情况,还能帮助我们对变化趋势进行初步的预测。但它也有自己的局限性,你知道是什么吗?
由于变量对应的数值有限,不能全面反映变量间的关系。
认知篇
比比谁更快
(3)婴儿在6个月,1周岁,2周岁时的体重分别大约是出生时的2倍,3倍,4倍.
自变量:时间 因变量:剩余油量
自变量:时间 因变量:水的温度
自变量:年龄 因变量:体重
指出下列实例中自变量与因变量
(1)随着时间推移,汽车在行驶中的剩余油量减少。
(2)烧一壶水,发现在一定时间内温度随时间的
变化而变化,即随时间的增加,温度逐渐增高.
要求:抢答.
认知篇
比比谁更快
改革开放30多年以来,中国人民生活实现了从温饱到小康的历史性的跨越,也就是说人民生活水平的质量逐年提高.在这个过程中,因变量是( )
A.经济发展 B.生活水平质量
C.时间 D.人民
要求:抢答.
B
认知篇
生活中还有哪些例子反映了
变量之间的关系呢?
其中谁是自变量?
谁是因变量呢?
七嘴八舌
知识巩固篇
知识巩固篇
1.某河受暴雨袭击,某天此河水的水位记录为下表:
时间/小时 0 4 8 12 16 20 24
水位/米 2 2.5 3 4 5 6 8
(1)上表中反映了哪两个变量之间的关系?
自变量和因变量各是什么?
(2)12时,水位是多少?
(3)哪一时段水位上升最快?
自变量:时间 因变量:水位
4米
20到24小时
比比谁更快
要求:抢答.
知识巩固篇
研究表明,土豆的产量与氮肥的施用量有如下关系:
(1)上表反映了哪两个变量之间的关系?
是自变量, 是因变量.
(3)根据表格,你认为氮肥的施用量是 时
比较适宜?说说你的理由。
(4)粗略说一说氮肥的施用量对土豆产量的影响。
氮肥施用量 千克/公顷 0 34 67 101 135 202 256 336 404 471
土豆产量 吨/公顷 15.18 21.36 25.72 32.29 34.03 39.45 43.25 43.46 40.83 30.75
氮肥施用量
(2)当氮肥的施用量是101千克/公顷时,土豆的产量
是 ,如果不施氮肥呢?
32.29吨 /公顷
土豆产量
要求:先独立思考后举手回答.
知识巩固篇
用弹簧做挂重物实验,每增加100g,弹簧长度增加1cm,实验数据如下表:
质量(g) 100 200 300 400
长度(cm) 11 12 13 14
(1)在这个实验中,物体的质量是_______量,弹簧
的长度是________量;
自变
因变
(2) 请你预测所挂物体质量为800g时,弹簧总长度是_______若弹簧总长度为15厘米时,所挂物体的质量是________;
(3)不挂物体时弹簧的长度是________ 。
18厘米
500g
10厘米
要求:先组内讨论后举手回答.
知识巩固篇
测量弹簧秤挂重物后的长度
我们在弹簧秤上不断地加上砝码,研究砝码个数
与弹簧长度之间的变化情况,并记录在下表:
砝码个数 1 2 3
读数 5 10 15
问题:若砝码个数为4个,弹簧秤上的读数
会是多少呢?
若10个呢?
n个呢?
实 验
知识巩固篇
(1)上述变化中自变量是 ,因变量是 。
(2)第5排有 个座位,第6排有 个座位。
(3)第n排有 个 座位。
排数
万达电影院地面一部分是扇形,座位按下列方式设置:
座位数
76
80
(56+4n)
排数 1 2 3 4
座位数 60 64 68 72
…… n
……
生活链接接篇
生活链接篇
夏天房中的温度高达40.9℃,现打开空调降温,室内
的温度与空调打开的时间有如下关系:
时间/分 0 2 4 6 8 10 12 14 16 18
温度/℃ 40.9 39.6 38.3 37 35.7 34.4 33.1 31.8 30.5 29.2
①上表反映了哪两变量之间的关系?
自变量和因变量各是什么?
②如果用t表示时间、T表示温度,那么随着t的变化T的变化
趋势是什么?
③若要使温度降到24℃,估计还需多少分钟?
生活链接篇
在某地,人们发现某种蟋蟀叫的次数与温度之间有如下的近似关系:记录蟋蟀每分钟叫的次数,用这个数除以7,然后再加上3就得到当时的温度.小刚同学在不同时间记录了蟋蟀每分钟叫的次数,分别是98次,105次,119次,133次,154次,请你帮助小刚计算出当时的温度,并用表格将它们之间的关系反映出来,并指出上述关系中的自变量和因变量.
生活链接篇
蟋蟀每分钟叫的次数 98 105 119 133 154
当时的温度
17
18
20
22
25
问题:请你描述一下蟋蟀每分钟叫的次数与当时的温度有怎样的关系?
蟋蟀每分钟叫的次数÷7+3=当时的温度.
当堂检测
小红帮助妈妈预算家庭4月份电费开支情况,下表是小红家4 月份连续8天早晨电表显示的读数:
(1)表中反映的自变量是 ,因变量是 ;
(2)估计小红家4 月份每天用电量是 度;
(3)若每度电的电费是0.6元,估计她家4 月份(按30天算)应交的电费是____元.
日期 1 2 3 4 5 6 7 8
电表读数(度) 21 24 28 33 39 42 46 49
日期
电表读数
4
72
知识小结
通过今天的学习,用你自己的话说说你的收获和体会
1.在具体情境中准确找到自变量、因变量以及常量。
2.能从表格中获得变量之间关系的信息,
能用表格表示变量之间的关系,
尝试对变化趋势进行初步的预测。
3.能发现生活中的变量,体会数学中的变量对生活的实际价值。
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
