人教版八年级下册 20.1.2 平均数、中位数和众数的应用课件(共19张PPT)
文档属性
| 名称 | 人教版八年级下册 20.1.2 平均数、中位数和众数的应用课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 136.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-15 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
第二十章 数据的分析
20.1.2 中位数和众数
第2课时 平均数、中位数和众数的应用
情景导入
员工 总工程师 副经理 技术员A 技术员B 技术员C 技术员D 技术员E 技术员F 临时员G
工资 5000 4000 1800 1700 1500 1200 1200 1200 400
下表是某公司月工资报表:
请大家仔细观察表中的数据,计算该公司员工的月平均工资是多少
平均月工资能否客观地反映员工的实际收入
不能,因为平均数容易受极端值的影响.
答:平均工资是2000元.
极端值是指一组数据中与其余数据差异很大的数据.
情景导入
某公司月工资报表:
(3)你认为用什么数据反映一般技术员工的收入比较合适?试说明理由
答:我认为用中位数1500元.因为中位数不受特别大和特别小的数据的影响,能反映一组数据的中等水平.
员工 总工程师 副经理 技术员A 技术员B 技术员C 技术员D 技术员E 技术员F 临时员G
工资 5000 4000 1800 1700 1500 1200 1200 1200 400
情景导入
(4)你认为用什么数据反映多数人的收入比较合适?试说明理由.
答:我认为用众数1200元.因为众数同样不受特别大和特别小的数据的影响,它能反映一组数据的多数水平.
员工 总工程师 副经理 技术员A 技术员B 技术员C 技术员D 技术员E 技术员F 临时员G
工资 5000 4000 1800 1700 1500 1200 1200 1200 400
某公司月工资报表:
合作探究
由上节的学习内容我们知道,平均数、中位数和众数都是用来代表一组数据的,而且,它们互相之间可以相等也可以不相等,没有固定的大小关系.当它们不全相等的时候,就产生了最终选用哪一特征数来代表一组数据的问题了.
活动:探究平均数、 中位数及众数的使用
合作探究
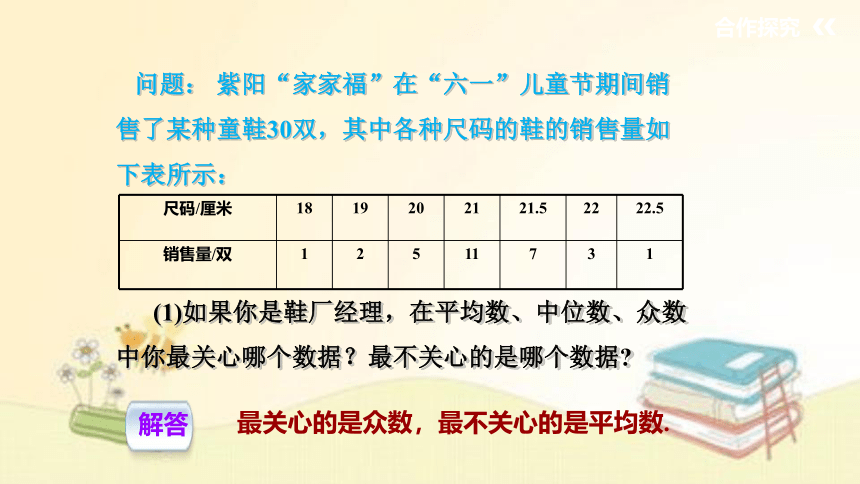
问题: 紫阳“家家福”在“六一”儿童节期间销售了某种童鞋30双,其中各种尺码的鞋的销售量如下表所示:
尺码/厘米 18 19 20 21 21.5 22 22.5
销售量/双 1 2 5 11 7 3 1
(1)如果你是鞋厂经理,在平均数、中位数、众数中你最关心哪个数据?最不关心的是哪个数据
解答
最关心的是众数,最不关心的是平均数.
合作探究
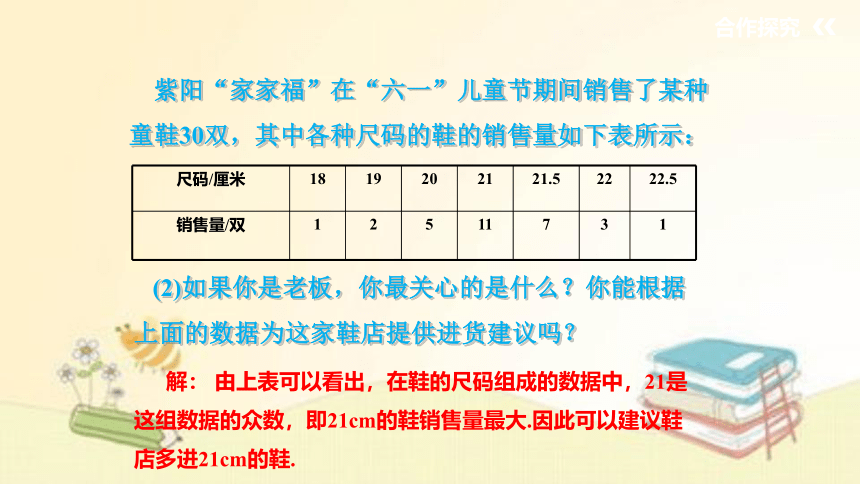
紫阳“家家福”在“六一”儿童节期间销售了某种童鞋30双,其中各种尺码的鞋的销售量如下表所示:
尺码/厘米 18 19 20 21 21.5 22 22.5
销售量/双 1 2 5 11 7 3 1
(2)如果你是老板,你最关心的是什么?你能根据上面的数据为这家鞋店提供进货建议吗?
解: 由上表可以看出,在鞋的尺码组成的数据中,21是这组数据的众数,即21cm的鞋销售量最大.因此可以建议鞋店多进21cm的鞋.
合作探究
我们看各类比赛,当评委亮分后,主持人总要说去掉一个最高分,去掉一个最低分,最后的分……为什么一定要去掉最高分和最低分来求平均分呢 你知道吗
你知道吗
因为平均数很敏感,当数据中含有极个别特别大或特别小的数据时,平均数就不能很好的反映一般水平,而去掉最高分和最低分来求平均分,是为了减少极端数据对平均分的影响.
知识要点
平均数的计算要用到所有数据,它能够充分利用数据提供的信息,因此在现实生活中较为常用,但它受极端值的影响较大.
当一组数据中某个数据多次重复出现时,众数往往是人们关心的一个量,众数不受极端值的影响,这是它的一个优势.
中位数只需要很少的计算,不受极端值的影响,这在有些情况下是一个优点.
知识要点
温馨提示:(1)平均数、中位数和众数都是用来代表一组数据的一些特征.
平均数反映一组数据的平均水平;
中位数反映一组数据的中等水平;
众数反映一组数据的多数水平.
(2)三个统计量不总是有意义,它们有各自的使用范围.在具体问题中要合理选用它们.
知识要点
例1 某公司10名销售员,去年完成的销售额情况如下表:
(1)求销售额的平均数、众数、中位数;
销售额(单位:万元) 3 4 5 6 7 8 10
销售人员数(单位:人) 1 3 2 1 1 1 1
解:(1)平均数为5.6万元 众数为4万元 中位数为5万元.
知识要点
例1 某公司10名销售员,去年完成的销售额情况如下表:
(2)如果想确定一个较高的销售目标,你认为月销售额多少合适?说明理由.
销售额(单位:万元) 3 4 5 6 7 8 10
销售人员数(单位:人) 1 3 2 1 1 1 1
解:(2)如果想确定一个较高的销售目标,这个目标可以定为每月5.6万元.因为从上表数据看,在平均数、中位数和众数中,平均数最大。可以估计,月销售额定为每月5.6万元是一个较高目标,大约会有2/5的销售员可以完成.
解题小结
(1)解决这类问题,先要通过分析表中数据的平均数、中位数、众数的情况;(2)确定一个适当的月销售目标是一个关键问题。如果目标定得太高,多数销售员完不成任务,会使销售员失去信心;如果目标定得太低,不能发挥营业员的潜力.
解题小结
某大商场策划了一次“还利给顾客”活动,凡一次购物100元以上(含100元)均可当场抽奖.奖金分配见下表:
奖金
等级
一等奖
二等奖
三等奖
四等奖
幸运奖
奖金数额/元
15000
8000
1000
80
20
中奖
人次
4
10
70
360
560
商场欺骗顾客了吗?
商场提醒:平均每份奖金249元!
解题小结
你认为商场的说法能够很好的代表中奖的一般金额吗?商场欺骗顾客了吗?说说你的看法,以后我们在遇到开奖问题应该关心什么?
中奖
顾客
商场在欺骗我们顾客,我们中只有两人获得80元,其他人都是20元,可气!
解题小结
商场没有欺骗顾客,因为奖金的平均数确实是249元,但是奖金的平均数不能很好地代表中奖的一般金额,91.6%的奖卷的奖金不超过80元.如果遇到开奖问题应该关心中奖金额的众数等数据信息.
奖金
等级
一等奖
二等奖
三等奖
四等奖
幸运奖
奖金数额/元
15000
8000
1000
80
20
中奖
人次
4
10
70
360
560
课堂小结
1.平均数、中位数、众数的特征
2.平均数、中位数、众数的使用方法
平均数是最常用的指标,它表示“一般水平”,中位数表示“中等水平”,众数表示“多数水平”.
(1)没有极端值,数据相差不大时,选用平均数有较强的代表性;如评价学生成绩用平均分,班级学生平均身高,裁判一般以平均成绩为选手最终得分等.
课堂小结
(2)有特别大或特别小的数据时就不能用平均数,而是用中位数比较好 ;如知道某学生在班上是处于中上水平还是中下水平,应选用中位数.
(3)当数据有明显集中趋势时,宜使用众数.日常生活中诸如“最佳”、“最受欢迎”、“最满意”等.
在实际选用时,要记住三个统计量并不总是有意义的,不总是合适的,都有各自不同的适用范围.
谢 谢!
第二十章 数据的分析
20.1.2 中位数和众数
第2课时 平均数、中位数和众数的应用
情景导入
员工 总工程师 副经理 技术员A 技术员B 技术员C 技术员D 技术员E 技术员F 临时员G
工资 5000 4000 1800 1700 1500 1200 1200 1200 400
下表是某公司月工资报表:
请大家仔细观察表中的数据,计算该公司员工的月平均工资是多少
平均月工资能否客观地反映员工的实际收入
不能,因为平均数容易受极端值的影响.
答:平均工资是2000元.
极端值是指一组数据中与其余数据差异很大的数据.
情景导入
某公司月工资报表:
(3)你认为用什么数据反映一般技术员工的收入比较合适?试说明理由
答:我认为用中位数1500元.因为中位数不受特别大和特别小的数据的影响,能反映一组数据的中等水平.
员工 总工程师 副经理 技术员A 技术员B 技术员C 技术员D 技术员E 技术员F 临时员G
工资 5000 4000 1800 1700 1500 1200 1200 1200 400
情景导入
(4)你认为用什么数据反映多数人的收入比较合适?试说明理由.
答:我认为用众数1200元.因为众数同样不受特别大和特别小的数据的影响,它能反映一组数据的多数水平.
员工 总工程师 副经理 技术员A 技术员B 技术员C 技术员D 技术员E 技术员F 临时员G
工资 5000 4000 1800 1700 1500 1200 1200 1200 400
某公司月工资报表:
合作探究
由上节的学习内容我们知道,平均数、中位数和众数都是用来代表一组数据的,而且,它们互相之间可以相等也可以不相等,没有固定的大小关系.当它们不全相等的时候,就产生了最终选用哪一特征数来代表一组数据的问题了.
活动:探究平均数、 中位数及众数的使用
合作探究
问题: 紫阳“家家福”在“六一”儿童节期间销售了某种童鞋30双,其中各种尺码的鞋的销售量如下表所示:
尺码/厘米 18 19 20 21 21.5 22 22.5
销售量/双 1 2 5 11 7 3 1
(1)如果你是鞋厂经理,在平均数、中位数、众数中你最关心哪个数据?最不关心的是哪个数据
解答
最关心的是众数,最不关心的是平均数.
合作探究
紫阳“家家福”在“六一”儿童节期间销售了某种童鞋30双,其中各种尺码的鞋的销售量如下表所示:
尺码/厘米 18 19 20 21 21.5 22 22.5
销售量/双 1 2 5 11 7 3 1
(2)如果你是老板,你最关心的是什么?你能根据上面的数据为这家鞋店提供进货建议吗?
解: 由上表可以看出,在鞋的尺码组成的数据中,21是这组数据的众数,即21cm的鞋销售量最大.因此可以建议鞋店多进21cm的鞋.
合作探究
我们看各类比赛,当评委亮分后,主持人总要说去掉一个最高分,去掉一个最低分,最后的分……为什么一定要去掉最高分和最低分来求平均分呢 你知道吗
你知道吗
因为平均数很敏感,当数据中含有极个别特别大或特别小的数据时,平均数就不能很好的反映一般水平,而去掉最高分和最低分来求平均分,是为了减少极端数据对平均分的影响.
知识要点
平均数的计算要用到所有数据,它能够充分利用数据提供的信息,因此在现实生活中较为常用,但它受极端值的影响较大.
当一组数据中某个数据多次重复出现时,众数往往是人们关心的一个量,众数不受极端值的影响,这是它的一个优势.
中位数只需要很少的计算,不受极端值的影响,这在有些情况下是一个优点.
知识要点
温馨提示:(1)平均数、中位数和众数都是用来代表一组数据的一些特征.
平均数反映一组数据的平均水平;
中位数反映一组数据的中等水平;
众数反映一组数据的多数水平.
(2)三个统计量不总是有意义,它们有各自的使用范围.在具体问题中要合理选用它们.
知识要点
例1 某公司10名销售员,去年完成的销售额情况如下表:
(1)求销售额的平均数、众数、中位数;
销售额(单位:万元) 3 4 5 6 7 8 10
销售人员数(单位:人) 1 3 2 1 1 1 1
解:(1)平均数为5.6万元 众数为4万元 中位数为5万元.
知识要点
例1 某公司10名销售员,去年完成的销售额情况如下表:
(2)如果想确定一个较高的销售目标,你认为月销售额多少合适?说明理由.
销售额(单位:万元) 3 4 5 6 7 8 10
销售人员数(单位:人) 1 3 2 1 1 1 1
解:(2)如果想确定一个较高的销售目标,这个目标可以定为每月5.6万元.因为从上表数据看,在平均数、中位数和众数中,平均数最大。可以估计,月销售额定为每月5.6万元是一个较高目标,大约会有2/5的销售员可以完成.
解题小结
(1)解决这类问题,先要通过分析表中数据的平均数、中位数、众数的情况;(2)确定一个适当的月销售目标是一个关键问题。如果目标定得太高,多数销售员完不成任务,会使销售员失去信心;如果目标定得太低,不能发挥营业员的潜力.
解题小结
某大商场策划了一次“还利给顾客”活动,凡一次购物100元以上(含100元)均可当场抽奖.奖金分配见下表:
奖金
等级
一等奖
二等奖
三等奖
四等奖
幸运奖
奖金数额/元
15000
8000
1000
80
20
中奖
人次
4
10
70
360
560
商场欺骗顾客了吗?
商场提醒:平均每份奖金249元!
解题小结
你认为商场的说法能够很好的代表中奖的一般金额吗?商场欺骗顾客了吗?说说你的看法,以后我们在遇到开奖问题应该关心什么?
中奖
顾客
商场在欺骗我们顾客,我们中只有两人获得80元,其他人都是20元,可气!
解题小结
商场没有欺骗顾客,因为奖金的平均数确实是249元,但是奖金的平均数不能很好地代表中奖的一般金额,91.6%的奖卷的奖金不超过80元.如果遇到开奖问题应该关心中奖金额的众数等数据信息.
奖金
等级
一等奖
二等奖
三等奖
四等奖
幸运奖
奖金数额/元
15000
8000
1000
80
20
中奖
人次
4
10
70
360
560
课堂小结
1.平均数、中位数、众数的特征
2.平均数、中位数、众数的使用方法
平均数是最常用的指标,它表示“一般水平”,中位数表示“中等水平”,众数表示“多数水平”.
(1)没有极端值,数据相差不大时,选用平均数有较强的代表性;如评价学生成绩用平均分,班级学生平均身高,裁判一般以平均成绩为选手最终得分等.
课堂小结
(2)有特别大或特别小的数据时就不能用平均数,而是用中位数比较好 ;如知道某学生在班上是处于中上水平还是中下水平,应选用中位数.
(3)当数据有明显集中趋势时,宜使用众数.日常生活中诸如“最佳”、“最受欢迎”、“最满意”等.
在实际选用时,要记住三个统计量并不总是有意义的,不总是合适的,都有各自不同的适用范围.
谢 谢!
