高中数学必修一 第一章并集与交集
文档属性
| 名称 | 高中数学必修一 第一章并集与交集 |  | |
| 格式 | zip | ||
| 文件大小 | 421.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-06 20:00:35 | ||
图片预览











文档简介
课件33张PPT。1.1.3 集合的基本运算第一课时 并集与交集提出问题1.对于两个集合A、B,二者之间一定具有包含关系吗?试举例说明. 2.两个实数可以进行加、减、乘、除四则运算,那么两个集合是否也可以进行某种运算呢? 知识探究(一): 并集考察下列两组集合:
(1)A={1,3,5},B={1,2,3,4},C={1,2,3,4,5};
(2) , , .思考1:上述两组集合中,集合A,B与集合C的关系如何?思考2:我们把上述集合C称为集合A与B的并集,一般地,如何定义集合A与B的并集?提示:由所有属于集合A或属于集合B的元素组成的集合,称为集合A与B的并集.思考3:我们用符号“ ”表示集合A与B的并集,并读
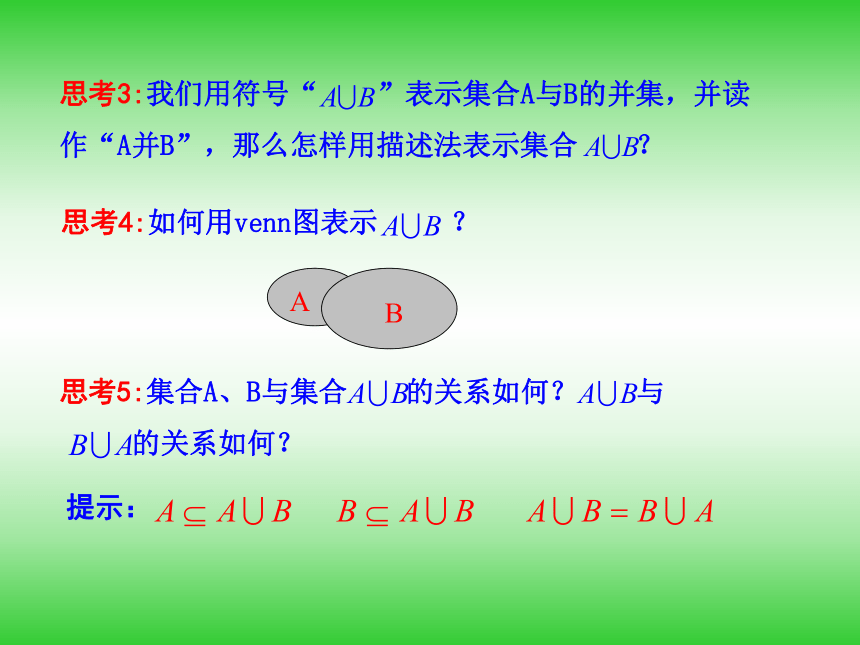
作“A并B”,那么怎样用描述法表示集合 ?思考4:如何用venn图表示 ?思考5:集合A、B与集合 的关系如何? 与
的关系如何?提示:思考6:集合 , 分别等于什么?思考8:若 ,则说明什么?提示:提示:提示:知识探究(二):交集考察下列两组集合:
(1)A={1,3,5},B={1,2,3,4},C={1,3};
(2) , , 思考1:上述两组集合中,集合A,B与集合C的关系如何?思考2:我们把上述集合C称为集合A与B的交集,一般地,如何定义集合A与B的交集?提示:由属于集合A且属于集合B的所有元素组成的集合,称为集合A与B的交集.思考3:我们用符号“ ”表示集合A与B的并集,
并读作“A交B”,那么怎样用描述法表示集合 ?思考4:如何用venn图表示 ?思考5:集合A、B与集合 的关系如何? 与
关系如何?提示:思考6:集合 , 分别等于什么?思考8:若 ,则说明什么?集合A与B没有公共元素或提示:提示:提示:理论迁移考点一: 交集、并集的简单运算[例1](1)(2011·福建高考)若集合M={-1,0,
1},N={0,1,2},则M∩N 等于( )
A.{0,1} B.{-1,0,1}
C.{0,1,2} D.{-1,0,1,2}(2)已知集合M={x|-35},则M∪N= ( )
A.{x|x<-5,或x>-3}
B.{x|-5C.{x|-3D.{x|x<-3,或x>5}[精解详析] (1)∵M={-1,0,1},N={0,1,2},
∴M∩N={-1,0,1}∩{0,1,2}={0,1}.
(2)借助数轴,M∪N={x|-35}={x|x<-5,或x>-3}.答案: (1)A (2)A (3)D[一点通] 解此类题目首先应看清集合中元素的范围,简化集合.若是用列举法表示的数集,可以根据交集、并集的定义直接观察或用Venn图表示出集合运算的结果;若是用描述法表示的数集,可借助数轴分析写出结果,此时要注意当端点不在集合中时,应用“空心点”表示.1.若集合A={0,1,2,3},B={1,2,4},则集合A∪B=( )
A.{0,1,2,3,4} B.{1,2,3,4}
C.{1,2} D.{0}
解析:由并集的概念,可得A∪B={0,1,2,3,4}.
答案:A2.若集合A={x|-2A∩B= ( )
A.{x|-1C.{x|-2解析:A∩B={x|-2 ={x|0答案:D考点二: 已知集合的交集、并集求参数[例2] 已知A={x|a<x≤a+8},B={x|x<-1,或x>5}.若A∪B=R,求a的取值范围.[精解详析]在数轴上标出集合A、B,如图.[一点通] 1.与不等式有关的集合的运算,利用数轴分析法直观清晰,易于理解.若出现参数应注意分类讨论,最后要归纳总结.
2.建立不等式时,要特别注意端点值是否能取到.最好是把端点值代入题目验证.3.已知集合A={x|x≤1},B={x|x≥a},且A∪B=R,
则实数a的取值范围是________.解析:如图所示.若A ∪B=R,则a≤1.答案:a≤14.设A={x|-3≤x≤3},B={y|y=-x2+t}.若A∩B
=?,则实数t的取值范围是 ( )
A.t<-3 B.t≤-3
C.t>3 D.t≥3解析:∵B={y|y≤t},又∵A∩B=?,
如图所示,∴t<-3.答案:A5.设集合A={a2,a+1,-3},B={a-3,2a-1,
a2+1},A∩B={-3},求实数a.
解:∵A∩B={-3},∴-3∈B.
∵a2+1≠-3,∴a-3=-3或2a-1=-3.①若a-3=-3,则a=0,
此时A={0,1,-3},B={-3,-1,1}.
但A∩B={1,-3}与已知A∩B={-3}矛盾,
∴a≠0.
②若2a-1=-3,则a=-1,
此时A={1,0,-3},B={-4,-3,2},A∩B={-3}.
综上可知a=-1.考点三: 交集、并集性质的应用[例3](12分)设A={x|x2+4x=0},B={x|x2+2(a+1)x+a2-1=0}.若A∩B=B,求a的取值范围.[精解详析] 由已知得A={-4,0}.
∵A∩B=B,∴B?A,则B=?,{-4},{0},
{-4,0}. (2分)
①若B=?,则Δ=4(a+1)2-4(a2-1)=8(a+1)<0,
得a<-1. (4分)[一点通] 1.在利用集合的交集、并集性质解题时,常常会遇到A∩B=A,A∪B=B等这类问题.解答时常借助交、并集的定义及上节学习的集合间的关系去分析,如A∩B=A?A?B,A∪B=B?A?B等.解答时应灵活处理.
2.当集合B?A时,如果集合A是一个确定的集合,而集合B不确定,运算时要考虑B=?的情况,切不可漏掉.6.已知集合A={x|-2≤x≤7},B={x|m+1若A∩B=B,则实数m的取值范围是________.答案:m≤47.已知集合A={1,3,x},B={1,x2},A∪B
={1,3,x},求满足条件的实数x的值.方法规律小结在集合运算过程中应力求做到“三化”.
(1)意义化:首先分清集合的类型,是表示数集、点集,还是某类图形;是表示函数的自变量的取值范围,或因变量的取值范围,还是表示方程或不等式的解集.(2)具体化:具体求出相关集合中函数的自变量、因变量的范围或方程、不等式的解集等;不能具体求出的,也应力求将相关集合转化为最简形式.
(3)直观化:借助数轴、直角坐标平面、Venn图等将有关集合直观地表示出来,从而借助数形结合思想解决问题.同学们 再见!
(1)A={1,3,5},B={1,2,3,4},C={1,2,3,4,5};
(2) , , .思考1:上述两组集合中,集合A,B与集合C的关系如何?思考2:我们把上述集合C称为集合A与B的并集,一般地,如何定义集合A与B的并集?提示:由所有属于集合A或属于集合B的元素组成的集合,称为集合A与B的并集.思考3:我们用符号“ ”表示集合A与B的并集,并读
作“A并B”,那么怎样用描述法表示集合 ?思考4:如何用venn图表示 ?思考5:集合A、B与集合 的关系如何? 与
的关系如何?提示:思考6:集合 , 分别等于什么?思考8:若 ,则说明什么?提示:提示:提示:知识探究(二):交集考察下列两组集合:
(1)A={1,3,5},B={1,2,3,4},C={1,3};
(2) , , 思考1:上述两组集合中,集合A,B与集合C的关系如何?思考2:我们把上述集合C称为集合A与B的交集,一般地,如何定义集合A与B的交集?提示:由属于集合A且属于集合B的所有元素组成的集合,称为集合A与B的交集.思考3:我们用符号“ ”表示集合A与B的并集,
并读作“A交B”,那么怎样用描述法表示集合 ?思考4:如何用venn图表示 ?思考5:集合A、B与集合 的关系如何? 与
关系如何?提示:思考6:集合 , 分别等于什么?思考8:若 ,则说明什么?集合A与B没有公共元素或提示:提示:提示:理论迁移考点一: 交集、并集的简单运算[例1](1)(2011·福建高考)若集合M={-1,0,
1},N={0,1,2},则M∩N 等于( )
A.{0,1} B.{-1,0,1}
C.{0,1,2} D.{-1,0,1,2}(2)已知集合M={x|-3
A.{x|x<-5,或x>-3}
B.{x|-5
∴M∩N={-1,0,1}∩{0,1,2}={0,1}.
(2)借助数轴,M∪N={x|-3
A.{0,1,2,3,4} B.{1,2,3,4}
C.{1,2} D.{0}
解析:由并集的概念,可得A∪B={0,1,2,3,4}.
答案:A2.若集合A={x|-2
A.{x|-1
2.建立不等式时,要特别注意端点值是否能取到.最好是把端点值代入题目验证.3.已知集合A={x|x≤1},B={x|x≥a},且A∪B=R,
则实数a的取值范围是________.解析:如图所示.若A ∪B=R,则a≤1.答案:a≤14.设A={x|-3≤x≤3},B={y|y=-x2+t}.若A∩B
=?,则实数t的取值范围是 ( )
A.t<-3 B.t≤-3
C.t>3 D.t≥3解析:∵B={y|y≤t},又∵A∩B=?,
如图所示,∴t<-3.答案:A5.设集合A={a2,a+1,-3},B={a-3,2a-1,
a2+1},A∩B={-3},求实数a.
解:∵A∩B={-3},∴-3∈B.
∵a2+1≠-3,∴a-3=-3或2a-1=-3.①若a-3=-3,则a=0,
此时A={0,1,-3},B={-3,-1,1}.
但A∩B={1,-3}与已知A∩B={-3}矛盾,
∴a≠0.
②若2a-1=-3,则a=-1,
此时A={1,0,-3},B={-4,-3,2},A∩B={-3}.
综上可知a=-1.考点三: 交集、并集性质的应用[例3](12分)设A={x|x2+4x=0},B={x|x2+2(a+1)x+a2-1=0}.若A∩B=B,求a的取值范围.[精解详析] 由已知得A={-4,0}.
∵A∩B=B,∴B?A,则B=?,{-4},{0},
{-4,0}. (2分)
①若B=?,则Δ=4(a+1)2-4(a2-1)=8(a+1)<0,
得a<-1. (4分)[一点通] 1.在利用集合的交集、并集性质解题时,常常会遇到A∩B=A,A∪B=B等这类问题.解答时常借助交、并集的定义及上节学习的集合间的关系去分析,如A∩B=A?A?B,A∪B=B?A?B等.解答时应灵活处理.
2.当集合B?A时,如果集合A是一个确定的集合,而集合B不确定,运算时要考虑B=?的情况,切不可漏掉.6.已知集合A={x|-2≤x≤7},B={x|m+1
={1,3,x},求满足条件的实数x的值.方法规律小结在集合运算过程中应力求做到“三化”.
(1)意义化:首先分清集合的类型,是表示数集、点集,还是某类图形;是表示函数的自变量的取值范围,或因变量的取值范围,还是表示方程或不等式的解集.(2)具体化:具体求出相关集合中函数的自变量、因变量的范围或方程、不等式的解集等;不能具体求出的,也应力求将相关集合转化为最简形式.
(3)直观化:借助数轴、直角坐标平面、Venn图等将有关集合直观地表示出来,从而借助数形结合思想解决问题.同学们 再见!
