高中数学必修一第一章分段函数与映射
文档属性
| 名称 | 高中数学必修一第一章分段函数与映射 |  | |
| 格式 | zip | ||
| 文件大小 | 522.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-06 20:05:56 | ||
图片预览








文档简介
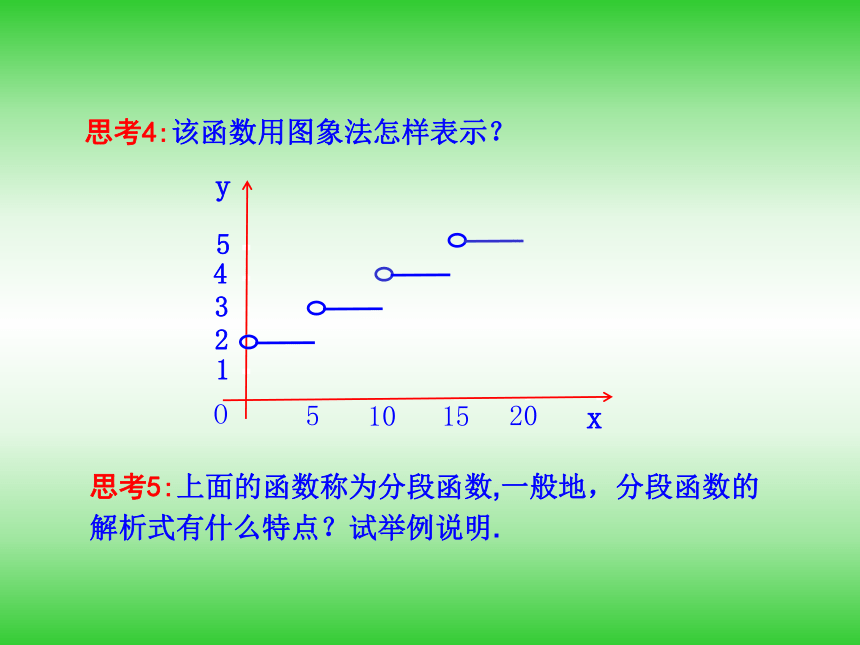
课件34张PPT。1.2.2 函数的表示方法第二课时 分段函数与映射提出问题1.设集合A={x|x是正方形},B={y|y>0},对应关系f:正方形→面积,那么从集合A到集合B的对应是否是函数?为什么?2.函数是“两个数集A、B间的一种确定的对应关系”,如果集合A、B不都是数集,这种对应关系又怎样解释呢?知识探究(一):分段函数某市某条公交线路的总里程是20公里,在这条线路上公交车“招手即停”,其票价如下:
(1)5公里以内(含5公里),票价2元;
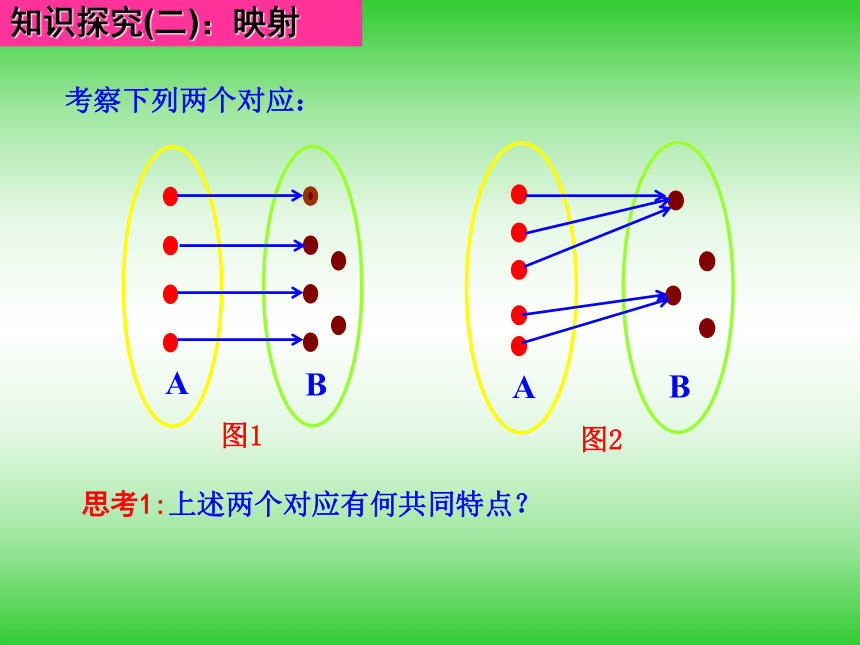
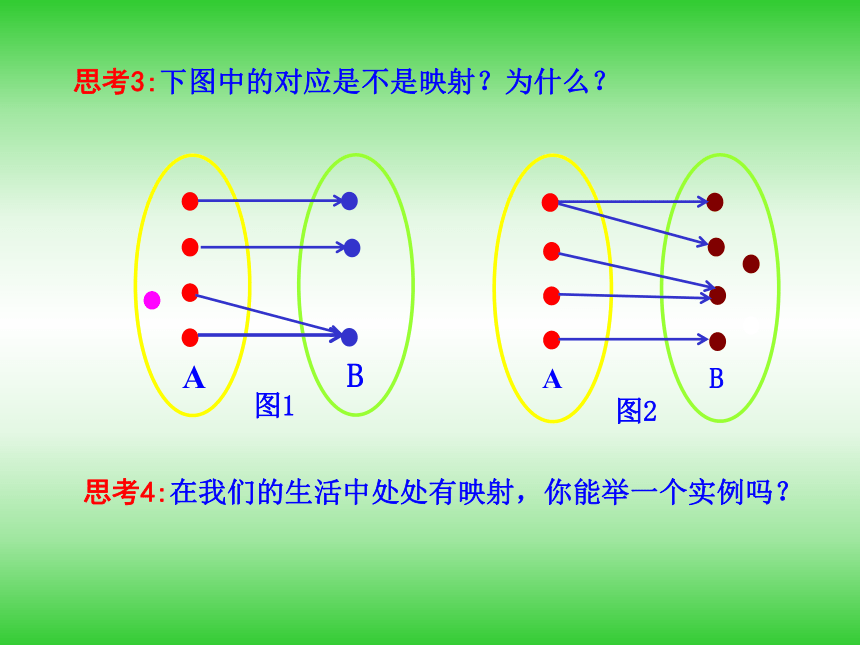
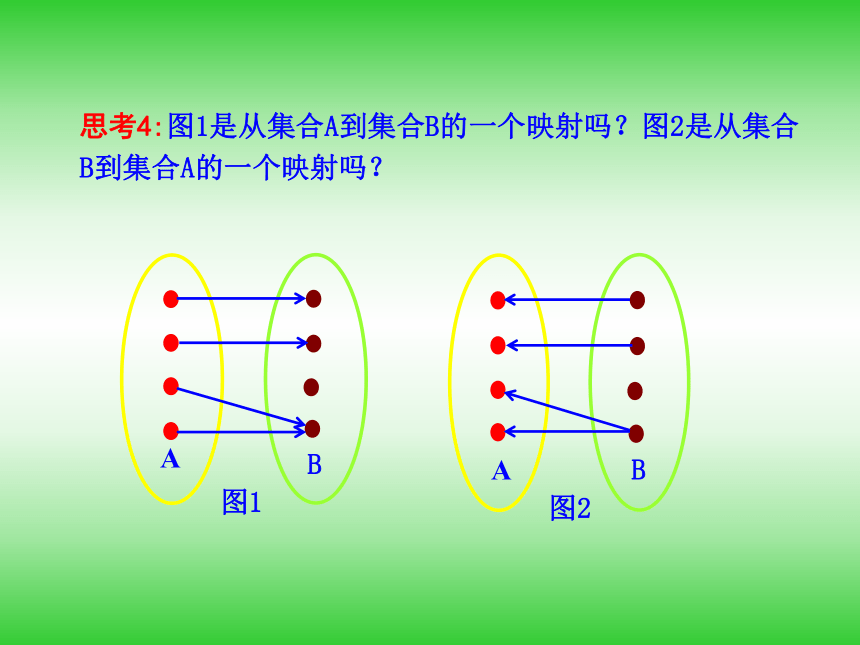
(2)5公里以上,每增加5公里,票价增加1元(不足5公里按照5公里计算).思考1:里程与票价之间的对应关系是否为函数?若是,函数的自变量是什么?定义域是什么?思考2:该函数用解析法怎样表示?提示:设里程为x公里,票价为y元,则思考3:该函数用列表法怎样表示?思考4:该函数用图象法怎样表示? 思考5:上面的函数称为分段函数,一般地,分段函数的解析式有什么特点?试举例说明. 知识探究(二):映射思考1:上述两个对应有何共同特点?思考2:我们把具有上述特点的对应叫做映射,那么如何定义映射?提示:设A、B是两个非空的集合,如果按某一个确定的对应关系f,使对于集合A中的任意一个元素x,在集合B中都有唯一确定的元素y与之对应,那么就称对应f:A→B为从集合A到集合B的一个映射.思考4:在我们的生活中处处有映射,你能举一个实例吗?知识探究(二):映射与函数的关系思考1:函数一定是映射吗?映射一定是函数吗?思考2:映射有哪几种对应形式? 一对一,多对一. 思考3:设集合A=N,B={x|x是非负偶数},你能给出一个对应关系f,使从集合A到集合B的对应是一个映射吗?并指出其对应形式.提示: 思考5:有人说映射有“三性”,即“有序性”,“存在性”和“唯一性”,对此你是怎样理解的?③“唯一性”:对于集合A中的任何一个元素,在集合B中和它对应的元素是唯一的.①“有序性”:映射是有方向的,A到B的映射与B到A的映射往往不是同一个映射;②“存在性”:对于集合A中的任何一个元素,集合B中都存在元素和它对应;提示:理论迁移考点一: 映射的概念[精解详析] (1)A中元素3在对应关系f的作用下与3的差的绝对值为0,而0 B,故不是映射.
(2)因为一个圆有无数个内接矩形,即集合A中任何一个元素在集合B中有无数个元素与之对应,故不是映射.[一点通] 给定两个非空集合A,B及对应关系f,判断是否是从集合A到集合B的映射,主要利用映射的定义判断是否满足对集合A中的任何一个元素,在集合B中都有唯一的元素和它对应.A→B的对应有“多对一”“一对一”“一对多”,前两种对应是A到B的映射,而最后一种不是A到B的映射.1.设映射f:A→B,则下列命题中,正确的是( )
A.A中每个元素在B中必有唯一元素与其对应
B.B中每个元素在A中必有元素与其对应
C.B中每个元素在A中的对应元素唯一
D.A中不同的元素在B中的对应元素必不同解析:f:A→B表示A中的任一元素在B中都有唯一元素与之对应,而B中的元素可以不参与对应,也可以和A中多个元素对应.
答案:A2.下列集合A到集合B的对应f是映射的是 ( )
A.A={-1,0,1},B={-1,0,1},f:A中的数平方
B.A={0,1},B={-1,0,1},f:A中的数开平方
C.A=Z,B=Q,f:A中的数取倒数
D.A=R,B={正实数},f:A中的数取绝对值解析:在B中,集合A中的元素1有±1两个元素与之对应,∴B不正确.C中,集合A中的元素0没有倒数,∴C不正确.D中,集合A中的元素0的绝对值仍然是0,而0?B,∴D不正确.
答案:A答案:C考点二: 分段函数(2)当a≤-2时,a+1=3,
即a=2>-2,不合题意,舍去.
当-2<a<2时,a2+2a=3,即a2+2a-3=0.
所以(a-1)(a+3)=0,得a=1,或a=-3.
∵1∈(-2,2),-3 (-2,2),∴a=1符合题意.
当a≥2时,2a-1=3,即a=2符合题意.
综上可得,当f(a)=3时,a=1,或a=2.[一点通] 1.分段函数求值,一定要注意所给自变量的值所在的范围,代入相应的解析式求值.
2.多层“f”的问题,要按照“由里到外”的顺序,层层处理.
3.已知分段函数的函数值求相对应的自变量的值,可分段利用函数解析式求得自变量的值,但应注意检验分段解析式的适用范围;也可先判断每一段上的函数值的范围,确定解析式再求解.解析:∵-4<1,∴f(-4)=16,f(16)=16-1=15.
答案:A解析:f(1)=f(1-1)=f(0)=0.
答案:D答案:(4,+∞)[精解详析] (1)利用描点法,作出f(x)的图象,如图所示.(6分)
考点三: 分段函数应用(2)由条件知,函数f(x)的定义域为R. (8分)
由图象知,当-1≤x≤1时,f(x)=x2的值域为[0,1],
当x>1或x<-1时,f(x)=1,
所以f(x)的值域为[0,1]. (12分)[一点通] 1.分段函数的解析式因其特点可以分成两个或两个以上的不同部分,所以它的图象也由几部分构成,可以是光滑的曲线段,也可以是一些孤立的点或几段线段,而分段函数的定义域与值域的最好求法也是“图象法”.2.对含有绝对值的函数,要作其图象,首先根据绝对值的意义去掉绝对值符号,将函数转化为分段函数来画图象.
3.画分段函数图象时还要注意端点是“实心点”还是“空心点”.(2)函数f(x)的图象如图所示.(3)由(2)知,f(x)在(-2,2]上的值域为[1,3).方法规律小结1.对映射的定义,应注意以下几点:
(1)集合A和B必须是非空集合,它们可以是数集、点集,也可以是其他集合.
(2)映射是一种特殊的对应.对应关系可以用图示或文字描述的方法来表达.2.理解分段函数应注意的问题:
(1)分段函数是一个函数,其定义域是各段“定义域”的并集,其值域是各段“值域”的并集.写定义域时,区间的端点需不重不漏.(2)求分段函数的函数值时,自变量的取值属于哪一段,就用哪一段的解析式.
(3)研究分段函数时,应根据“先分后合”的原则,尤其是作分段函数的图象时,可先将各段的图象分别画出来,从而得到整个函数的图象.同学们 再见!
(1)5公里以内(含5公里),票价2元;
(2)5公里以上,每增加5公里,票价增加1元(不足5公里按照5公里计算).思考1:里程与票价之间的对应关系是否为函数?若是,函数的自变量是什么?定义域是什么?思考2:该函数用解析法怎样表示?提示:设里程为x公里,票价为y元,则思考3:该函数用列表法怎样表示?思考4:该函数用图象法怎样表示? 思考5:上面的函数称为分段函数,一般地,分段函数的解析式有什么特点?试举例说明. 知识探究(二):映射思考1:上述两个对应有何共同特点?思考2:我们把具有上述特点的对应叫做映射,那么如何定义映射?提示:设A、B是两个非空的集合,如果按某一个确定的对应关系f,使对于集合A中的任意一个元素x,在集合B中都有唯一确定的元素y与之对应,那么就称对应f:A→B为从集合A到集合B的一个映射.思考4:在我们的生活中处处有映射,你能举一个实例吗?知识探究(二):映射与函数的关系思考1:函数一定是映射吗?映射一定是函数吗?思考2:映射有哪几种对应形式? 一对一,多对一. 思考3:设集合A=N,B={x|x是非负偶数},你能给出一个对应关系f,使从集合A到集合B的对应是一个映射吗?并指出其对应形式.提示: 思考5:有人说映射有“三性”,即“有序性”,“存在性”和“唯一性”,对此你是怎样理解的?③“唯一性”:对于集合A中的任何一个元素,在集合B中和它对应的元素是唯一的.①“有序性”:映射是有方向的,A到B的映射与B到A的映射往往不是同一个映射;②“存在性”:对于集合A中的任何一个元素,集合B中都存在元素和它对应;提示:理论迁移考点一: 映射的概念[精解详析] (1)A中元素3在对应关系f的作用下与3的差的绝对值为0,而0 B,故不是映射.
(2)因为一个圆有无数个内接矩形,即集合A中任何一个元素在集合B中有无数个元素与之对应,故不是映射.[一点通] 给定两个非空集合A,B及对应关系f,判断是否是从集合A到集合B的映射,主要利用映射的定义判断是否满足对集合A中的任何一个元素,在集合B中都有唯一的元素和它对应.A→B的对应有“多对一”“一对一”“一对多”,前两种对应是A到B的映射,而最后一种不是A到B的映射.1.设映射f:A→B,则下列命题中,正确的是( )
A.A中每个元素在B中必有唯一元素与其对应
B.B中每个元素在A中必有元素与其对应
C.B中每个元素在A中的对应元素唯一
D.A中不同的元素在B中的对应元素必不同解析:f:A→B表示A中的任一元素在B中都有唯一元素与之对应,而B中的元素可以不参与对应,也可以和A中多个元素对应.
答案:A2.下列集合A到集合B的对应f是映射的是 ( )
A.A={-1,0,1},B={-1,0,1},f:A中的数平方
B.A={0,1},B={-1,0,1},f:A中的数开平方
C.A=Z,B=Q,f:A中的数取倒数
D.A=R,B={正实数},f:A中的数取绝对值解析:在B中,集合A中的元素1有±1两个元素与之对应,∴B不正确.C中,集合A中的元素0没有倒数,∴C不正确.D中,集合A中的元素0的绝对值仍然是0,而0?B,∴D不正确.
答案:A答案:C考点二: 分段函数(2)当a≤-2时,a+1=3,
即a=2>-2,不合题意,舍去.
当-2<a<2时,a2+2a=3,即a2+2a-3=0.
所以(a-1)(a+3)=0,得a=1,或a=-3.
∵1∈(-2,2),-3 (-2,2),∴a=1符合题意.
当a≥2时,2a-1=3,即a=2符合题意.
综上可得,当f(a)=3时,a=1,或a=2.[一点通] 1.分段函数求值,一定要注意所给自变量的值所在的范围,代入相应的解析式求值.
2.多层“f”的问题,要按照“由里到外”的顺序,层层处理.
3.已知分段函数的函数值求相对应的自变量的值,可分段利用函数解析式求得自变量的值,但应注意检验分段解析式的适用范围;也可先判断每一段上的函数值的范围,确定解析式再求解.解析:∵-4<1,∴f(-4)=16,f(16)=16-1=15.
答案:A解析:f(1)=f(1-1)=f(0)=0.
答案:D答案:(4,+∞)[精解详析] (1)利用描点法,作出f(x)的图象,如图所示.(6分)
考点三: 分段函数应用(2)由条件知,函数f(x)的定义域为R. (8分)
由图象知,当-1≤x≤1时,f(x)=x2的值域为[0,1],
当x>1或x<-1时,f(x)=1,
所以f(x)的值域为[0,1]. (12分)[一点通] 1.分段函数的解析式因其特点可以分成两个或两个以上的不同部分,所以它的图象也由几部分构成,可以是光滑的曲线段,也可以是一些孤立的点或几段线段,而分段函数的定义域与值域的最好求法也是“图象法”.2.对含有绝对值的函数,要作其图象,首先根据绝对值的意义去掉绝对值符号,将函数转化为分段函数来画图象.
3.画分段函数图象时还要注意端点是“实心点”还是“空心点”.(2)函数f(x)的图象如图所示.(3)由(2)知,f(x)在(-2,2]上的值域为[1,3).方法规律小结1.对映射的定义,应注意以下几点:
(1)集合A和B必须是非空集合,它们可以是数集、点集,也可以是其他集合.
(2)映射是一种特殊的对应.对应关系可以用图示或文字描述的方法来表达.2.理解分段函数应注意的问题:
(1)分段函数是一个函数,其定义域是各段“定义域”的并集,其值域是各段“值域”的并集.写定义域时,区间的端点需不重不漏.(2)求分段函数的函数值时,自变量的取值属于哪一段,就用哪一段的解析式.
(3)研究分段函数时,应根据“先分后合”的原则,尤其是作分段函数的图象时,可先将各段的图象分别画出来,从而得到整个函数的图象.同学们 再见!
