高中数学必修一第一章函数的三种表示方法
文档属性
| 名称 | 高中数学必修一第一章函数的三种表示方法 |  | |
| 格式 | zip | ||
| 文件大小 | 486.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-06 20:08:23 | ||
图片预览








文档简介
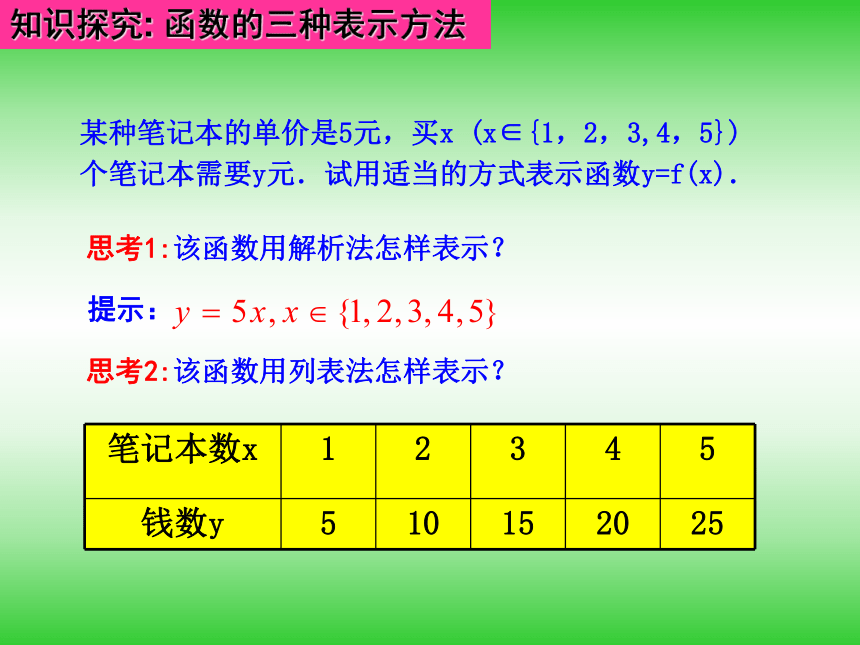
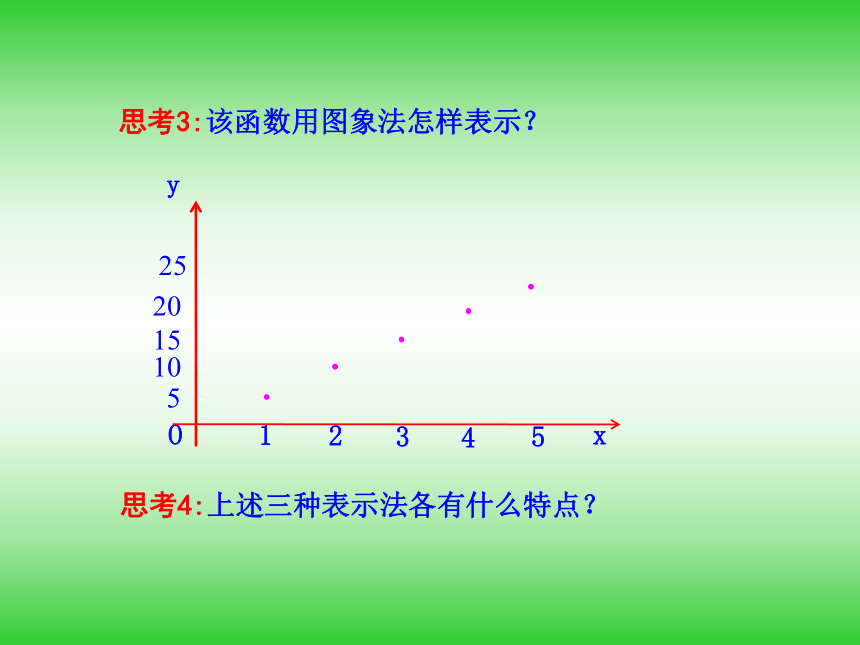
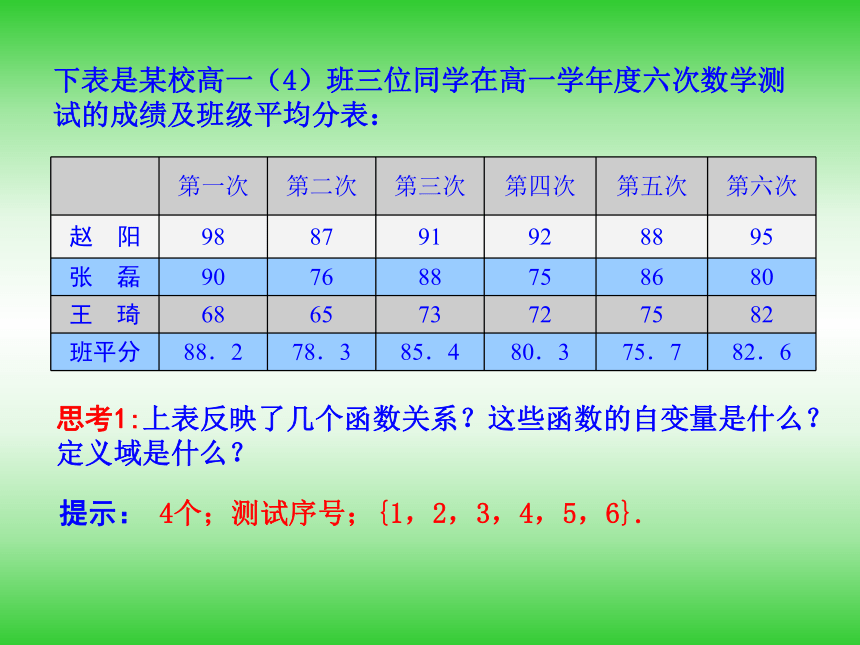
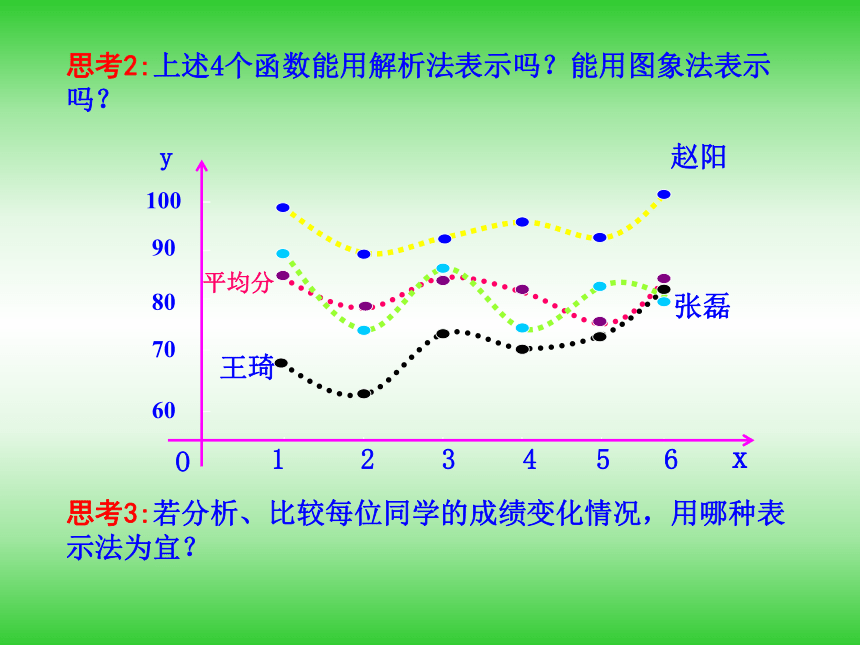
课件30张PPT。1.2.2 函数的表示方法第一课时 函数的三种表示方法提出问题1.从集合与对应的观点分析,函数的定义是什么?2.函数有哪几种常用的表示法?3.在日常生活中,我们会遇到许多函数问题,如何选择适当的方式来表示问题中的函数关系呢?知识探究: 函数的三种表示方法某种笔记本的单价是5元,买x (x∈{1,2,3,4,5})个笔记本需要y元.试用适当的方式表示函数y=f(x).思考1:该函数用解析法怎样表示?思考2:该函数用列表法怎样表示?提示:思考3:该函数用图象法怎样表示? 思考4:上述三种表示法各有什么特点?下表是某校高一(4)班三位同学在高一学年度六次数学测试的成绩及班级平均分表: 思考1:上表反映了几个函数关系?这些函数的自变量是什么?定义域是什么?4个;测试序号;{1,2,3,4,5,6}. 提示:思考2:上述4个函数能用解析法表示吗?能用图象法表示吗?思考3:若分析、比较每位同学的成绩变化情况,用哪种表示法为宜?理论迁移考点一: 用待定系数法求函数解析式[例1] (1)已知反比例函数f(x)满足f(3)=-6,求f(x)的解析式;
(2)一次函数y=f(x),f(1)=1,f(-1)=-3,求f(3).[一点通] 1.求函数解析式实际上就是寻找函数三要素中的对应关系.
2.当已知函数的类型时,可设出其函数解析式,利用待定系数法求解,这里包含着方程思想的应用.1.已知f(x)是一次函数,且f(f(x))=4x+3,求f(x).2.已知f(x)是二次函数,且满足f(0)=0,f(x+1)-f(x)
=2x,求f(x)的解析式.考点二: 用换元法、配凑法求函数解析式3.已知f(x+1)=x2+4x+1,求f(x)的解析式.解:设x+1=t,则x=t-1,
f(t)=(t-1)2+4(t-1)+1,即f(t)=t2+2t-2.
∴所求函数为f(x)=x2+2x-2.考点三: 函数的图象及应用(2分)图象如图.(2)y=x2+2x=(x+1)2-1,x∈[-2,2].
图象是抛物线y=x2+2x在[-2,2]上的部分,如图所示.(10分) 由图,可得函数的值域是[-1,8]. (12分)[一点通] 作函数图象主要有三步:列表、描点、连线.作图象时一般应先确定函数的定义域,再在定义域内化简函数解析式,再列表画出图象,并标注一些关键点,如与坐标轴的交点、最高点、最低点等.5.函数y=f(x)的图象如图,则f(x)的
定义域是 ( )
A.R
B.(-∞,1)∪(1,+∞)
C.(-∞,0)∪(0,+∞)
D.(-1,0)解析:由图象知x≠0,即x∈(-∞,0)∪(0,+∞).
答案:C解:(1)当x=0时,y=1;
当x=2时,y=5.
所画图象如图1所示.
(2)y=x2-2x=(x-1)2-1.
当x=-1时,y=3.
当x=0时,y=0.
当x=1时,y=-1.
当x=2时,y=0.所画图象如图2所示.(3)当x=2时,y=1,其图象如图3所示.方法规律小结1.函数的三种表示法的优缺点比较:2.作函数图象时应注意以下几点:
(1)在定义域内作图;
(2)图象是实线或实点,定义域外的部分有时可用虚线来衬托整个图象;
(3)要标出某些关键点,例如图象的顶点、端点与坐标轴的交点等.要分清这些关键点是实心点还是空心点.同学们 再见!
(2)一次函数y=f(x),f(1)=1,f(-1)=-3,求f(3).[一点通] 1.求函数解析式实际上就是寻找函数三要素中的对应关系.
2.当已知函数的类型时,可设出其函数解析式,利用待定系数法求解,这里包含着方程思想的应用.1.已知f(x)是一次函数,且f(f(x))=4x+3,求f(x).2.已知f(x)是二次函数,且满足f(0)=0,f(x+1)-f(x)
=2x,求f(x)的解析式.考点二: 用换元法、配凑法求函数解析式3.已知f(x+1)=x2+4x+1,求f(x)的解析式.解:设x+1=t,则x=t-1,
f(t)=(t-1)2+4(t-1)+1,即f(t)=t2+2t-2.
∴所求函数为f(x)=x2+2x-2.考点三: 函数的图象及应用(2分)图象如图.(2)y=x2+2x=(x+1)2-1,x∈[-2,2].
图象是抛物线y=x2+2x在[-2,2]上的部分,如图所示.(10分) 由图,可得函数的值域是[-1,8]. (12分)[一点通] 作函数图象主要有三步:列表、描点、连线.作图象时一般应先确定函数的定义域,再在定义域内化简函数解析式,再列表画出图象,并标注一些关键点,如与坐标轴的交点、最高点、最低点等.5.函数y=f(x)的图象如图,则f(x)的
定义域是 ( )
A.R
B.(-∞,1)∪(1,+∞)
C.(-∞,0)∪(0,+∞)
D.(-1,0)解析:由图象知x≠0,即x∈(-∞,0)∪(0,+∞).
答案:C解:(1)当x=0时,y=1;
当x=2时,y=5.
所画图象如图1所示.
(2)y=x2-2x=(x-1)2-1.
当x=-1时,y=3.
当x=0时,y=0.
当x=1时,y=-1.
当x=2时,y=0.所画图象如图2所示.(3)当x=2时,y=1,其图象如图3所示.方法规律小结1.函数的三种表示法的优缺点比较:2.作函数图象时应注意以下几点:
(1)在定义域内作图;
(2)图象是实线或实点,定义域外的部分有时可用虚线来衬托整个图象;
(3)要标出某些关键点,例如图象的顶点、端点与坐标轴的交点等.要分清这些关键点是实心点还是空心点.同学们 再见!
