高中数学必修一第一章函数的最大(小)值
文档属性
| 名称 | 高中数学必修一第一章函数的最大(小)值 |  | |
| 格式 | zip | ||
| 文件大小 | 520.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-06 20:10:29 | ||
图片预览







文档简介
课件36张PPT。第二课时 函数的最大(小)值1.3.1 函数的单调性与
最大(小)值提出问题1.确定函数的单调性有哪些手段和方法?2.函数图象上升与下降反映了函数的单调性,
如果函数的图象存在最高点或最低点,它又
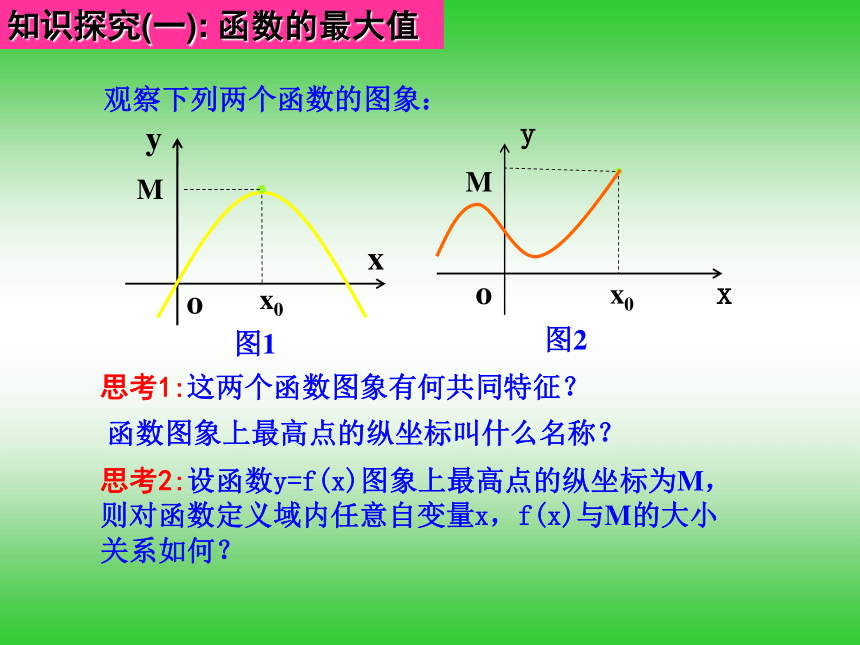
反映了函数的什么性质?知识探究(一): 函数的最大值观察下列两个函数的图象: 思考1:这两个函数图象有何共同特征?思考2:设函数y=f(x)图象上最高点的纵坐标为M,
则对函数定义域内任意自变量x,f(x)与M的大小
关系如何?函数图象上最高点的纵坐标叫什么名称?思考3:设函数 ,则 成立吗?
的最大值是2吗?为什么?思考4:怎样定义函数 的最大值?用什么符号
表示?思考5:函数的最大值是函数值域中的一个元
素吗?如果函数 的值域是(a,b),则函
数 存在最大值吗? 思考6:函数 有最大
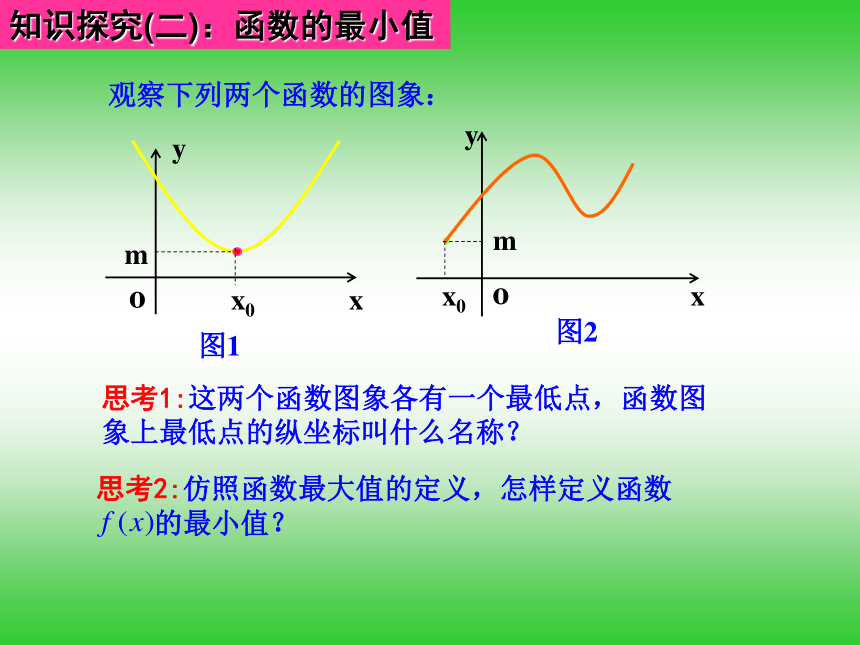
值吗?为什么?知识探究(二):函数的最小值观察下列两个函数的图象: 思考1:这两个函数图象各有一个最低点,函数图
象上最低点的纵坐标叫什么名称?思考2:仿照函数最大值的定义,怎样定义函数
的最小值? 一般地,设函数 的定义域为I,如果存在实
数M满足:
(1)对于任意的 , 都有 ;
(2)存在 ,使得 .
那么称m是函数 的最小值,记作知识探究(三):对函数最值的理解思考1:如果在函数 定义域内存在x1和 x2,
使对定义域内任意x都有
成立,由此你能得到什么结论?思考2:对一个函数就最大值和最小值的存在性而
言,有哪几种可能情况?思考3:如果函数 存在最大值,那么有几个?思考4:如果函数 的最大值是b,最小值是a,
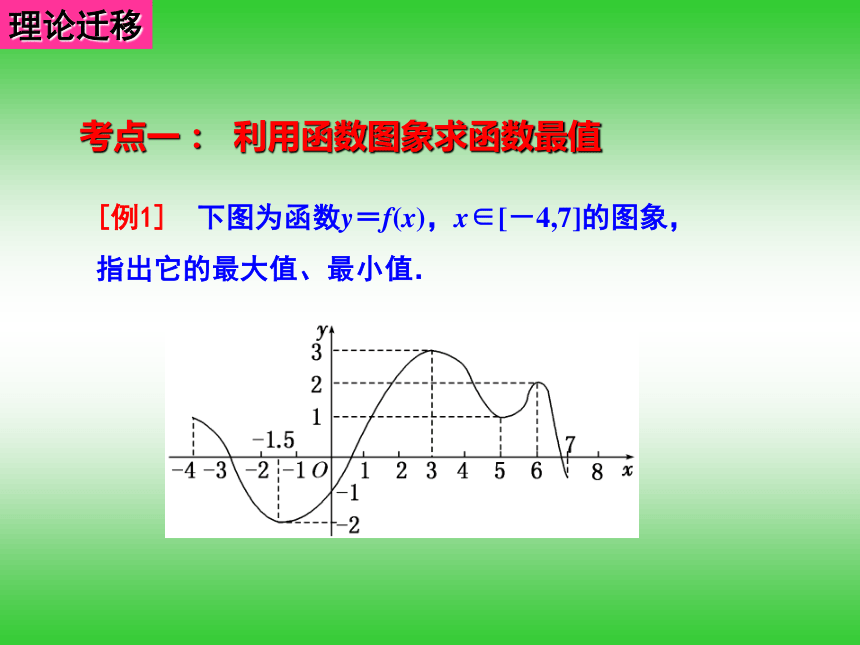
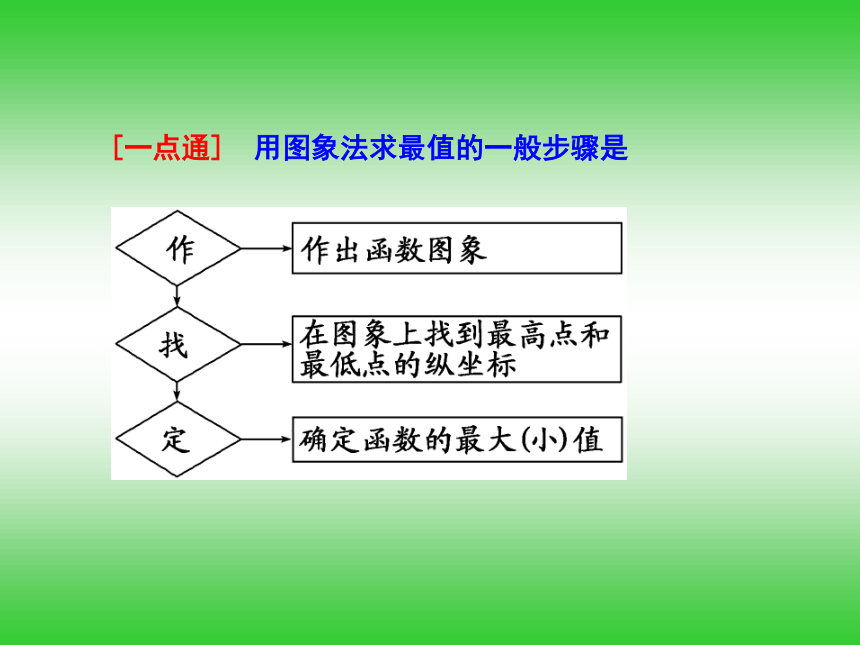
那么函数 的值域是[a,b]吗?理论迁移考点一: 利用函数图象求函数最值[例1] 下图为函数y=f(x),x∈[-4,7]的图象,指出它的最大值、最小值.[精解详析] 观察函数图象可以知道,图象上位置最高的点是(3,3),最低的点是(-1.5,-2),所以函数y=f(x)在x=3时取得最大值,即ymax=3,当x=-1.5时,取得最小值,即ymin=-2.[一点通] 用图象法求最值的一般步骤是解:画出函数的图象,如图所示.
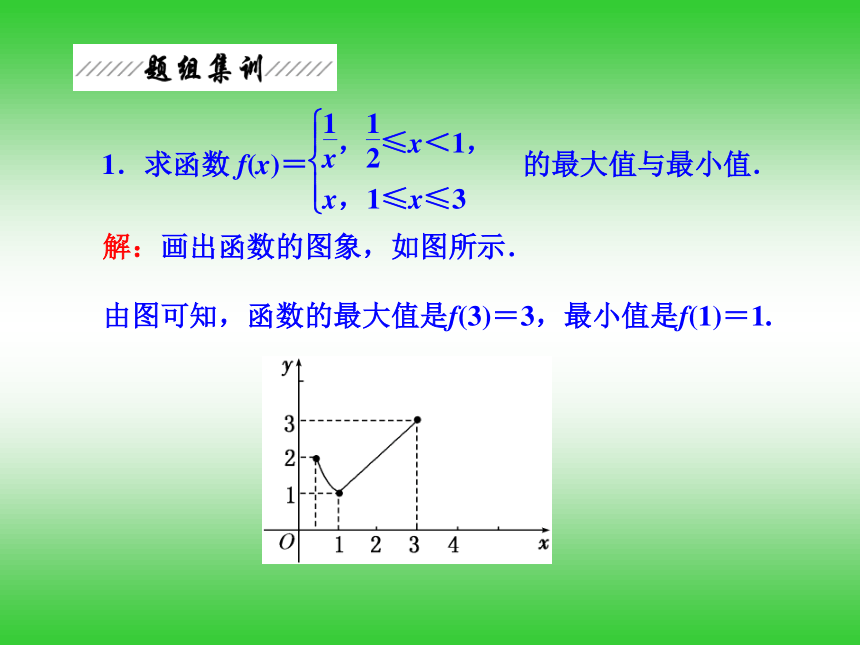
由图可知,函数的最大值是f(3)=3,最小值是f(1)=1.2.函数f(x)在区间[-2,5]上的图象如图所示,则此函数的最小值、最大值分别是 ( )
A.-2,f(2) B.2,f(2)
C.-2,f(5) D.2,f(5)解析:由函数的图象知,当x=-2时,有最小值-2;
当x=5时,有最大值f(5).
答案:C考点二: 利用函数单调性求函数最值[一点通] 函数的最值与单调性的关系
(1)如果函数y=f(x)在区间(a,b]上是增函数,在区间[b,c)上是减函数,则函数y=f(x),x∈(a,c)在x=b处有最大值f(b).
(2)如果函数y=f(x)在区间(a,b]上是减函数,在区间[b,c)上是增函数,则函数y=f(x),x∈(a,c)在x=b处有最小值f(b).(3)如果函数y=f(x)在区间[a,b]上是增(减)函数,则在区间[a,b]的左、右端点处分别取得最小(大)值、最大(小)值.答案:C考点三: 应用题中的最值问题(1)将利润表示为月产量的函数f(x);
(2)当月产量为何值时,公司所获利润最大?最大利润为多少元?(总收益=总成本+利润)[一点通]1.解决实际问题,首先要理解题意,然后建立数学模型转化成数学问题解决.
2.分清各种数据之间的关系是正确构造函数关系式的关键.
3.对于分段函数求最大(小)值时,要分别求出函数在各段上的最大(小)值,然后比较,最大(小)的一个即为函数的最大(小)值.6.某市一家报刊摊点,从该市报社买进该市的晚报价
格是每份0.40元,卖出价格是每份0.60元,卖不掉的报纸以每份0.05元的价格退回报社.在一个月(按30天计算)里,有18天每天可卖出400份,其余12天每天只能卖出180份.摊主每天从报社买进多少份晚报,才能使每月获得的利润最大(设摊主每天从报社买进晚报的份数是相同的)?解:设每天从报社买进x(180≤x≤400,x∈N*)份晚报,每月获利为y元,则有y=0.20(18x+12×180)-0.35×12(x-180)=-0.6x+1 188,180≤x≤400,x∈N*.
因为函数y=-0.6x+1 188在180≤x≤400,x∈N*时是减函数,所以x=180时函数取得最大值,最大值为
y=-0.6×180+1 188=1 080.
故摊主每天从报社买进180份晚报时,每月获得的利润最大,为1 080元.考点四: 与参数有关的最值问题[例4] (12分)求二次函数f(x)=x2-2ax+2在[2,4]上的最小值.[精解详析] ∵函数图象的对称轴是x=a, (1分)
∴当a<2时,
f(x)在[2,4]上是增函数,
∴f(x)min=f(2)=6-4a. (4分)
当a>4时,
f(x)在[2,4]上是减函数,
∴f(x)min=f(4)=18-8a. (7分)[一点通] 求二次函数的最值的一般步骤
(1)确定二次函数图像的对称轴.
(2)根据对称轴的位置情况讨论函数的单调性.
(3)写出最值.7.已知函数y=-x2-2ax(0≤x≤1),且ymax=a2,求实数a
的取值范围.解:∵y=-x2-2ax=-(x+a)2+a2(0≤x≤1),
∴函数图象是开口向下的抛物线,且对称轴为x=-a.
又∵ymax=a2,且0≤x≤1,
∴0≤-a≤1?-1≤a≤0.
∴实数a的取值范围是[-1,0].8.设f(x)=x2-4x-4,x∈[a,a+1](a∈R),求函
数f(x)的最小值g(a)的解析式.解:∵f(x)=(x-2)2-8,x∈[a,a+1],
∴当2∈[a,a+1]时,即1≤a≤2时,
g(a)=f(2)=-8.
当a+1<2,即a<1时,f(x)在[a,a+1]上是减函数,方法规律小结函数的值域与最大(小)值的区别
(1)函数的值域是一个集合,函数的最值是一个函数值,它是值域的一个元素,即定义域中一定存在一个x0,使f(x0)=M(最值).
(2)函数的值域一定存在,但函数并不一定有最大(小)值,如y=x在x∈(-1,1)时无最值.同学们 再见!
最大(小)值提出问题1.确定函数的单调性有哪些手段和方法?2.函数图象上升与下降反映了函数的单调性,
如果函数的图象存在最高点或最低点,它又
反映了函数的什么性质?知识探究(一): 函数的最大值观察下列两个函数的图象: 思考1:这两个函数图象有何共同特征?思考2:设函数y=f(x)图象上最高点的纵坐标为M,
则对函数定义域内任意自变量x,f(x)与M的大小
关系如何?函数图象上最高点的纵坐标叫什么名称?思考3:设函数 ,则 成立吗?
的最大值是2吗?为什么?思考4:怎样定义函数 的最大值?用什么符号
表示?思考5:函数的最大值是函数值域中的一个元
素吗?如果函数 的值域是(a,b),则函
数 存在最大值吗? 思考6:函数 有最大
值吗?为什么?知识探究(二):函数的最小值观察下列两个函数的图象: 思考1:这两个函数图象各有一个最低点,函数图
象上最低点的纵坐标叫什么名称?思考2:仿照函数最大值的定义,怎样定义函数
的最小值? 一般地,设函数 的定义域为I,如果存在实
数M满足:
(1)对于任意的 , 都有 ;
(2)存在 ,使得 .
那么称m是函数 的最小值,记作知识探究(三):对函数最值的理解思考1:如果在函数 定义域内存在x1和 x2,
使对定义域内任意x都有
成立,由此你能得到什么结论?思考2:对一个函数就最大值和最小值的存在性而
言,有哪几种可能情况?思考3:如果函数 存在最大值,那么有几个?思考4:如果函数 的最大值是b,最小值是a,
那么函数 的值域是[a,b]吗?理论迁移考点一: 利用函数图象求函数最值[例1] 下图为函数y=f(x),x∈[-4,7]的图象,指出它的最大值、最小值.[精解详析] 观察函数图象可以知道,图象上位置最高的点是(3,3),最低的点是(-1.5,-2),所以函数y=f(x)在x=3时取得最大值,即ymax=3,当x=-1.5时,取得最小值,即ymin=-2.[一点通] 用图象法求最值的一般步骤是解:画出函数的图象,如图所示.
由图可知,函数的最大值是f(3)=3,最小值是f(1)=1.2.函数f(x)在区间[-2,5]上的图象如图所示,则此函数的最小值、最大值分别是 ( )
A.-2,f(2) B.2,f(2)
C.-2,f(5) D.2,f(5)解析:由函数的图象知,当x=-2时,有最小值-2;
当x=5时,有最大值f(5).
答案:C考点二: 利用函数单调性求函数最值[一点通] 函数的最值与单调性的关系
(1)如果函数y=f(x)在区间(a,b]上是增函数,在区间[b,c)上是减函数,则函数y=f(x),x∈(a,c)在x=b处有最大值f(b).
(2)如果函数y=f(x)在区间(a,b]上是减函数,在区间[b,c)上是增函数,则函数y=f(x),x∈(a,c)在x=b处有最小值f(b).(3)如果函数y=f(x)在区间[a,b]上是增(减)函数,则在区间[a,b]的左、右端点处分别取得最小(大)值、最大(小)值.答案:C考点三: 应用题中的最值问题(1)将利润表示为月产量的函数f(x);
(2)当月产量为何值时,公司所获利润最大?最大利润为多少元?(总收益=总成本+利润)[一点通]1.解决实际问题,首先要理解题意,然后建立数学模型转化成数学问题解决.
2.分清各种数据之间的关系是正确构造函数关系式的关键.
3.对于分段函数求最大(小)值时,要分别求出函数在各段上的最大(小)值,然后比较,最大(小)的一个即为函数的最大(小)值.6.某市一家报刊摊点,从该市报社买进该市的晚报价
格是每份0.40元,卖出价格是每份0.60元,卖不掉的报纸以每份0.05元的价格退回报社.在一个月(按30天计算)里,有18天每天可卖出400份,其余12天每天只能卖出180份.摊主每天从报社买进多少份晚报,才能使每月获得的利润最大(设摊主每天从报社买进晚报的份数是相同的)?解:设每天从报社买进x(180≤x≤400,x∈N*)份晚报,每月获利为y元,则有y=0.20(18x+12×180)-0.35×12(x-180)=-0.6x+1 188,180≤x≤400,x∈N*.
因为函数y=-0.6x+1 188在180≤x≤400,x∈N*时是减函数,所以x=180时函数取得最大值,最大值为
y=-0.6×180+1 188=1 080.
故摊主每天从报社买进180份晚报时,每月获得的利润最大,为1 080元.考点四: 与参数有关的最值问题[例4] (12分)求二次函数f(x)=x2-2ax+2在[2,4]上的最小值.[精解详析] ∵函数图象的对称轴是x=a, (1分)
∴当a<2时,
f(x)在[2,4]上是增函数,
∴f(x)min=f(2)=6-4a. (4分)
当a>4时,
f(x)在[2,4]上是减函数,
∴f(x)min=f(4)=18-8a. (7分)[一点通] 求二次函数的最值的一般步骤
(1)确定二次函数图像的对称轴.
(2)根据对称轴的位置情况讨论函数的单调性.
(3)写出最值.7.已知函数y=-x2-2ax(0≤x≤1),且ymax=a2,求实数a
的取值范围.解:∵y=-x2-2ax=-(x+a)2+a2(0≤x≤1),
∴函数图象是开口向下的抛物线,且对称轴为x=-a.
又∵ymax=a2,且0≤x≤1,
∴0≤-a≤1?-1≤a≤0.
∴实数a的取值范围是[-1,0].8.设f(x)=x2-4x-4,x∈[a,a+1](a∈R),求函
数f(x)的最小值g(a)的解析式.解:∵f(x)=(x-2)2-8,x∈[a,a+1],
∴当2∈[a,a+1]时,即1≤a≤2时,
g(a)=f(2)=-8.
当a+1<2,即a<1时,f(x)在[a,a+1]上是减函数,方法规律小结函数的值域与最大(小)值的区别
(1)函数的值域是一个集合,函数的最值是一个函数值,它是值域的一个元素,即定义域中一定存在一个x0,使f(x0)=M(最值).
(2)函数的值域一定存在,但函数并不一定有最大(小)值,如y=x在x∈(-1,1)时无最值.同学们 再见!
