高中数学必修一第一章 奇偶性
图片预览










文档简介
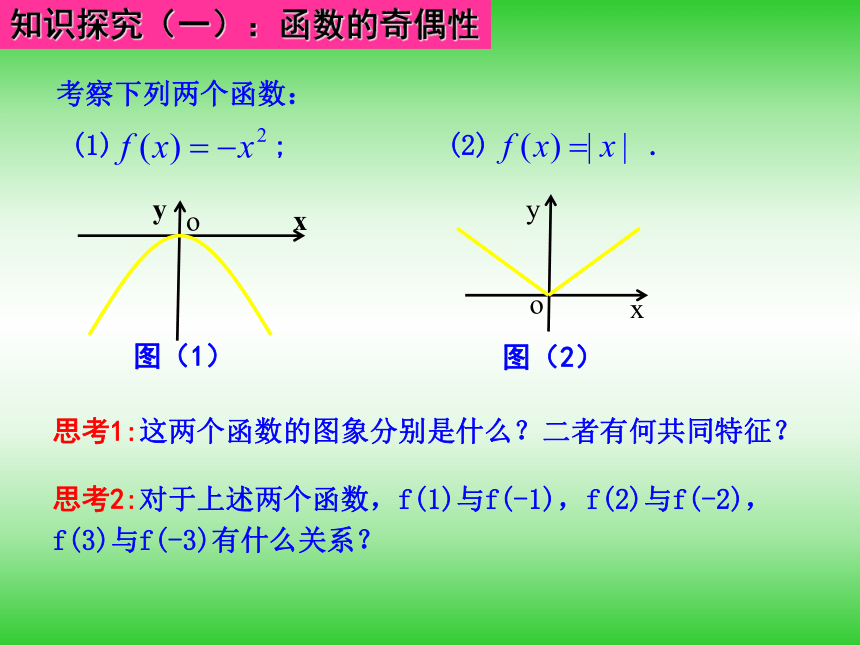
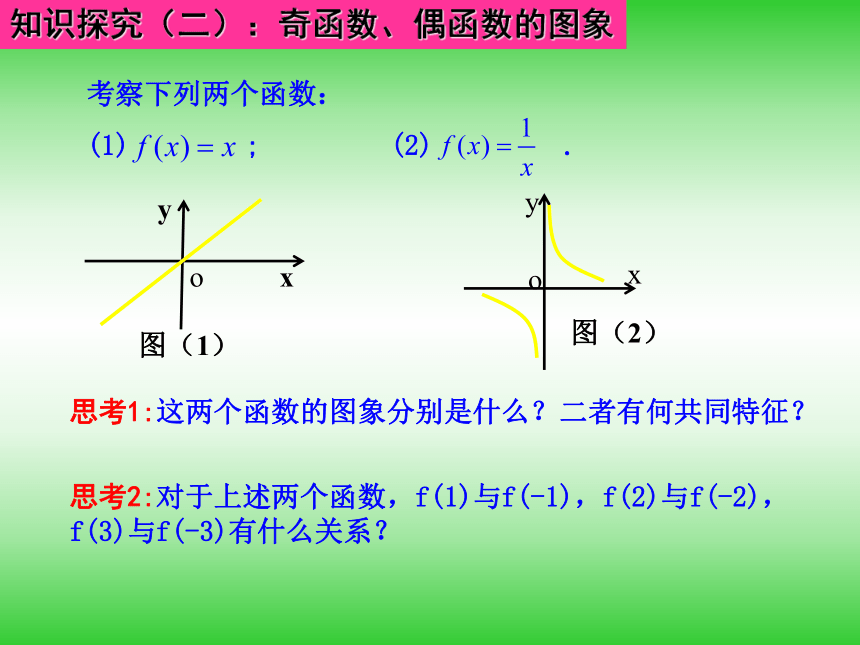
课件35张PPT。1.3.2 奇偶性提出问题1.研究函数的基本性质不仅是解决实际问题的需要,也是数学自身发展的必然结果. 例如事物的变化趋势,利润最大、效率最高等,这些特性反映在函数上,就是要研究函数的单调性及最值.2.我们从函数图象的升降变化引发了函数的单调性,从函数图象的最高点最低点引发了函数的最值,如果从函数图象的对称性出发又能得到什么性质?知识探究(一):函数的奇偶性思考1:这两个函数的图象分别是什么?二者有何共同特征? 思考2:对于上述两个函数,f(1)与f(-1),f(2)与f(-2),f(3)与f(-3)有什么关系? 思考3:一般地,若函数y=f(x)的图象关于y轴对称,则f(x)与f(-x)有什么关系?反之成立吗? 思考4:我们把具有上述特征的函数叫做偶函数,那么怎样定义偶函数?提示:如果对于函数f(x)定义域内的任意一个x,都有f(-x)=f(x)成立,则称函数f(x)为偶函数.f(x)=f(-x)提示:思考5:等式f(-x)=f(x)用文字语言怎样表述? 自变量相反时对应的函数值相等 偶函数的定义域关于原点对称提示: 提示: 知识探究(二):奇函数、偶函数的图象思考1:这两个函数的图象分别是什么?二者有何共同特征? 思考2:对于上述两个函数,f(1)与f(-1),f(2)与f(-2),f(3)与f(-3)有什么关系? 思考3:一般地,若函数y=f(x)的图象关于坐标原点对称,则f(x)与f(-x)有什么关系?反之成立吗? 思考4:我们把具有上述特征的函数叫做奇函数,那么怎样定义奇函数?提示:如果对于函数f(x)定义域内的任意一个x,都有f(-x)=-f(x)成立,则称函数f(x)为奇函数. f(x)=-f(-x)提示:思考5:等式f(-x)=-f(x)用文字语言怎样表述? 自变量相反时对应的函数值相反 奇函数的定义域关于原点对称提示:提示:理论迁移考点一: 函数奇偶性的判断[精解详析] (1)∵函数f(x)的定义域为R,关于原点对称,又f(-x)=2-|-x|=2-|x|=f(x),
∴f(x)为偶函数.
(2)∵函数f(x)的定义域为{-1,1},关于原点对称,且f(x)=0,又∵f(-x)=-f(x),f(-x)=f(x),
∴f(x)既是奇函数又是偶函数.(3)∵函数f(x)的定义域为{x|x≠1},不关于原点对称,
∴f(x)是非奇非偶函数.
(4)f(x)的定义域是(-∞,0)∪(0,+∞),关于原点对称.
当x>0时,-x<0,
f(-x)=1-(-x)=1+x=f(x);
当x<0时,-x>0,
f(-x)=1+(-x)=1-x=f(x).
综上可知,对于x∈(-∞,0)∪(0,+∞),
都有f(-x)=f(x),f(x)为偶函数.[一点通] 判断函数奇偶性的方法
(1)定义法:若函数定义域不关于原点对称,则函数为非奇非偶函数;若函数定义域关于原点对称,则应进一步判断f(-x)是否等于±f(x),或判断f(-x)±f(x)是否等于0,从而确定奇偶性.
(2)图象法:若函数图象关于原点对称,则函数为奇函数;若函数图象关于y轴对称,则函数为偶函数.解析:A、D两项,函数均为偶函数,B项中函数为非奇非偶函数,而C项中函数为奇函数.
答案:C2.若f(x)=ax2+bx+c(a≠0)是偶函数,则g(x)=ax3+bx2
+cx是 ( )
A.奇函数 B.偶函数
C.非奇非偶函数 D.奇函数又是偶函数解析:∵f(x)=ax2+bx+c是偶函数,
∴f(-x)=f(x),得b=0.∴g(x)=ax3+cx.
∴g(-x)=a(-x)3+c(-x)=-g(x),
∴g(x)为奇函数.
答案:A[例2] 如图,给出了偶函数
y=f(x)的局部图象,试比较f(1)
与f(3)的大小.
考点二: 奇偶函数的图象及应用[精解详析] 法一:∵函数f(x)是偶函数,
∴其图象关于y轴对称,如图.由图象可知f(1)又函数y=f(x)是偶函数,
∴f(-1)=f(1),f(-3)=f(3).
∴f(1)若当x∈[0,5]时,f(x)的图象如图所示,则不等式f(x)<0的解集是________.[例3] 已知函数f(x)(x∈R)是奇函数,且当x>0时,f(x)=2x-1,求函数f(x)的解析式.[精解详析] 当x<0时,-x>0,
∴f(-x)=2(-x)-1=-2x-1.
又∵f(x)是奇函数,∴f(-x)=-f(x).
∴f(x)=2x+1.
又f(x)(x∈R)是奇函数,
∴f(-0)=-f(0),考点三: 利用奇偶性求函数解析式[一点通] 解答该类问题的思路
(1)“求谁设谁”,即在哪个区间求解析式,x就设在哪个区间内.
(2)要利用已知区间的解析式进行代入.
(3)利用f(x)的奇偶性解出f(x).
注意,若函数f(x)的定义域内含0且为奇函数,则必有f(0)=0,但若为偶函数,则未必有f(0)=0.5.若定义在R上的偶函数f(x)和奇函数g(x)满足
f(x)+g(x)=x2+3x+1,则f(x)= ( )
A.x2 B.2x2
C.2x2+2 D.x2+1解析:∵f(x)+g(x)=x2+3x+1, ①
∴f(-x)+g(-x)=x2-3x+1.
又f(x)为偶函数,f(-x)=f(x);
g(x)为奇函数,g(-x)=-g(x),
∴f(x)-g(x)=x2-3x+1. ②
联立①②可得f(x)=x2+1.
答案:D6.已知f(x)是R上的偶函数,当x∈(0,+∞)时,f(x)=
x2+x-1,求x∈(-∞,0)时,f(x)的解析式.
解:设x<0,则-x>0.
∴f(-x)=(-x)2+(-x)-1.
∴f(-x)=x2-x-1.
∵函数f(x)是偶函数,∴f(-x)=f(x).
∴f(x)=x2-x-1.
∴当x∈(-∞,0)时,f(x)=x2-x-1.[一点通] 此类问题的解答思路是:先由函数的奇偶性将不等式两边都变成只含有“f”的式子,然后根据函数的单调性列出不等式(组)求解.列不等式(组)时,注意函数的定义域也是一个限制条件.7.已知函数f(x)在[-5,5]上是偶函数,f(x)在[0,5]上是
单调函数,且f(-4)A.f(-1)C.f(-3)f(1)解析:由f(x)是偶函数,得f(-4)又∵f(x)在[0,5]上是单调的,
∴f(x)在[0,5]上是减函数.
∴f(0)>f(1)>f(2)>f(3)>f(5).
而f(-1)=f(1),f(-3)=f(3),
故f(-1)>f(3),f(-3)>f(5),只有D正确.
答案:D答案:A1.函数的单调性与奇偶性的关系
(1)若f(x)是奇函数,则f(x)在其关于原点对称的区间上单调性一致;若f(x)是偶函数,则f(x)在其关于原点对称的区间上单调性相反.
(2)奇函数在对称区间上的最值相反,且互为相反数;偶函数在对称区间上的最值相等.方法规律小结2.分段函数奇偶性判定方法的关键是搞清x与-x的所在范围及其对应的函数关系式,并且函数在每一个区间上的奇偶性都应进行判断,最后综合得出在定义域内总有f(-x)=f(x)或f(-x)=-f(x),从而判定其奇偶性,而不能以其中一个区间来代替整个定义域.另外也可以用图象法来判断.同学们 再见!
∴f(x)为偶函数.
(2)∵函数f(x)的定义域为{-1,1},关于原点对称,且f(x)=0,又∵f(-x)=-f(x),f(-x)=f(x),
∴f(x)既是奇函数又是偶函数.(3)∵函数f(x)的定义域为{x|x≠1},不关于原点对称,
∴f(x)是非奇非偶函数.
(4)f(x)的定义域是(-∞,0)∪(0,+∞),关于原点对称.
当x>0时,-x<0,
f(-x)=1-(-x)=1+x=f(x);
当x<0时,-x>0,
f(-x)=1+(-x)=1-x=f(x).
综上可知,对于x∈(-∞,0)∪(0,+∞),
都有f(-x)=f(x),f(x)为偶函数.[一点通] 判断函数奇偶性的方法
(1)定义法:若函数定义域不关于原点对称,则函数为非奇非偶函数;若函数定义域关于原点对称,则应进一步判断f(-x)是否等于±f(x),或判断f(-x)±f(x)是否等于0,从而确定奇偶性.
(2)图象法:若函数图象关于原点对称,则函数为奇函数;若函数图象关于y轴对称,则函数为偶函数.解析:A、D两项,函数均为偶函数,B项中函数为非奇非偶函数,而C项中函数为奇函数.
答案:C2.若f(x)=ax2+bx+c(a≠0)是偶函数,则g(x)=ax3+bx2
+cx是 ( )
A.奇函数 B.偶函数
C.非奇非偶函数 D.奇函数又是偶函数解析:∵f(x)=ax2+bx+c是偶函数,
∴f(-x)=f(x),得b=0.∴g(x)=ax3+cx.
∴g(-x)=a(-x)3+c(-x)=-g(x),
∴g(x)为奇函数.
答案:A[例2] 如图,给出了偶函数
y=f(x)的局部图象,试比较f(1)
与f(3)的大小.
考点二: 奇偶函数的图象及应用[精解详析] 法一:∵函数f(x)是偶函数,
∴其图象关于y轴对称,如图.由图象可知f(1)
∴f(-1)=f(1),f(-3)=f(3).
∴f(1)
∴f(-x)=2(-x)-1=-2x-1.
又∵f(x)是奇函数,∴f(-x)=-f(x).
∴f(x)=2x+1.
又f(x)(x∈R)是奇函数,
∴f(-0)=-f(0),考点三: 利用奇偶性求函数解析式[一点通] 解答该类问题的思路
(1)“求谁设谁”,即在哪个区间求解析式,x就设在哪个区间内.
(2)要利用已知区间的解析式进行代入.
(3)利用f(x)的奇偶性解出f(x).
注意,若函数f(x)的定义域内含0且为奇函数,则必有f(0)=0,但若为偶函数,则未必有f(0)=0.5.若定义在R上的偶函数f(x)和奇函数g(x)满足
f(x)+g(x)=x2+3x+1,则f(x)= ( )
A.x2 B.2x2
C.2x2+2 D.x2+1解析:∵f(x)+g(x)=x2+3x+1, ①
∴f(-x)+g(-x)=x2-3x+1.
又f(x)为偶函数,f(-x)=f(x);
g(x)为奇函数,g(-x)=-g(x),
∴f(x)-g(x)=x2-3x+1. ②
联立①②可得f(x)=x2+1.
答案:D6.已知f(x)是R上的偶函数,当x∈(0,+∞)时,f(x)=
x2+x-1,求x∈(-∞,0)时,f(x)的解析式.
解:设x<0,则-x>0.
∴f(-x)=(-x)2+(-x)-1.
∴f(-x)=x2-x-1.
∵函数f(x)是偶函数,∴f(-x)=f(x).
∴f(x)=x2-x-1.
∴当x∈(-∞,0)时,f(x)=x2-x-1.[一点通] 此类问题的解答思路是:先由函数的奇偶性将不等式两边都变成只含有“f”的式子,然后根据函数的单调性列出不等式(组)求解.列不等式(组)时,注意函数的定义域也是一个限制条件.7.已知函数f(x)在[-5,5]上是偶函数,f(x)在[0,5]上是
单调函数,且f(-4)
∴f(x)在[0,5]上是减函数.
∴f(0)>f(1)>f(2)>f(3)>f(5).
而f(-1)=f(1),f(-3)=f(3),
故f(-1)>f(3),f(-3)>f(5),只有D正确.
答案:D答案:A1.函数的单调性与奇偶性的关系
(1)若f(x)是奇函数,则f(x)在其关于原点对称的区间上单调性一致;若f(x)是偶函数,则f(x)在其关于原点对称的区间上单调性相反.
(2)奇函数在对称区间上的最值相反,且互为相反数;偶函数在对称区间上的最值相等.方法规律小结2.分段函数奇偶性判定方法的关键是搞清x与-x的所在范围及其对应的函数关系式,并且函数在每一个区间上的奇偶性都应进行判断,最后综合得出在定义域内总有f(-x)=f(x)或f(-x)=-f(x),从而判定其奇偶性,而不能以其中一个区间来代替整个定义域.另外也可以用图象法来判断.同学们 再见!
