高中数学必修一第二章指数函数及其性质
文档属性
| 名称 | 高中数学必修一第二章指数函数及其性质 |

|
|
| 格式 | zip | ||
| 文件大小 | 524.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-06 00:00:00 | ||
图片预览







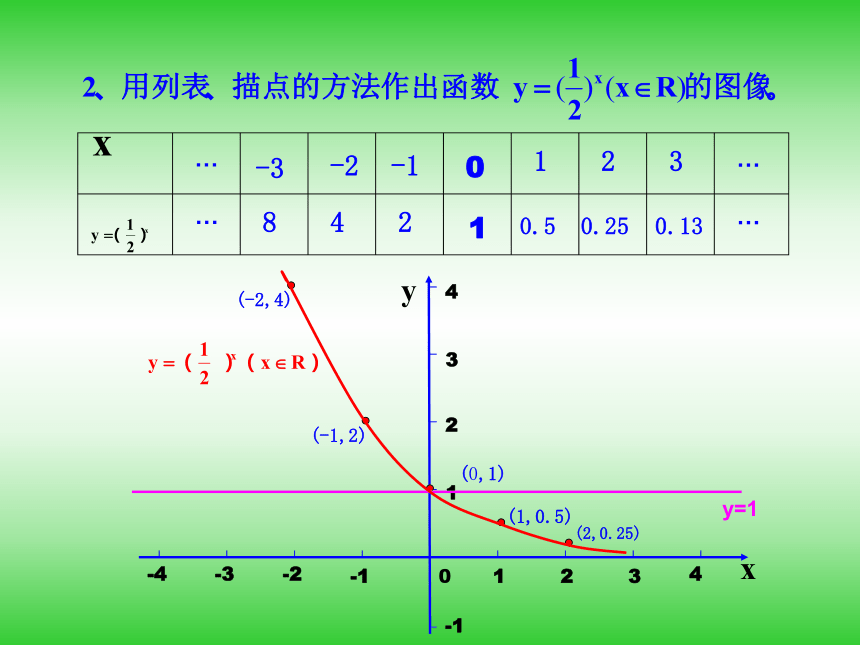
文档简介
课件39张PPT。2.1.2 指数函数的图象与性质第一课时 指数函数及其性质提出问题 思考:有一种细胞分裂时,由1个分裂成2个,2个分裂成4个,··· 1个这样的细胞分裂x次会得到多少个细胞?一个细胞未分裂时知识探究(一) 思考:有一种细胞分裂时,由1个分裂成2个,2个 分裂成4个,··· 1个这样的细胞分裂x次会得到多少个细胞?细胞第一次分裂后一个变为二个一分为二 思考:有一种细胞分裂时,由1个分裂成2个,2个分裂成4个,··· 1个这样的细胞分裂x次会得到多少个细胞?细胞第二次分裂后一个变为四个二分为四 思考:有一种细胞分裂时,由1个分裂成2个,2个 分裂成4个,··· 1个这样的细胞分裂x次会得到多少个细胞?细胞第三次分裂后一个变为八个
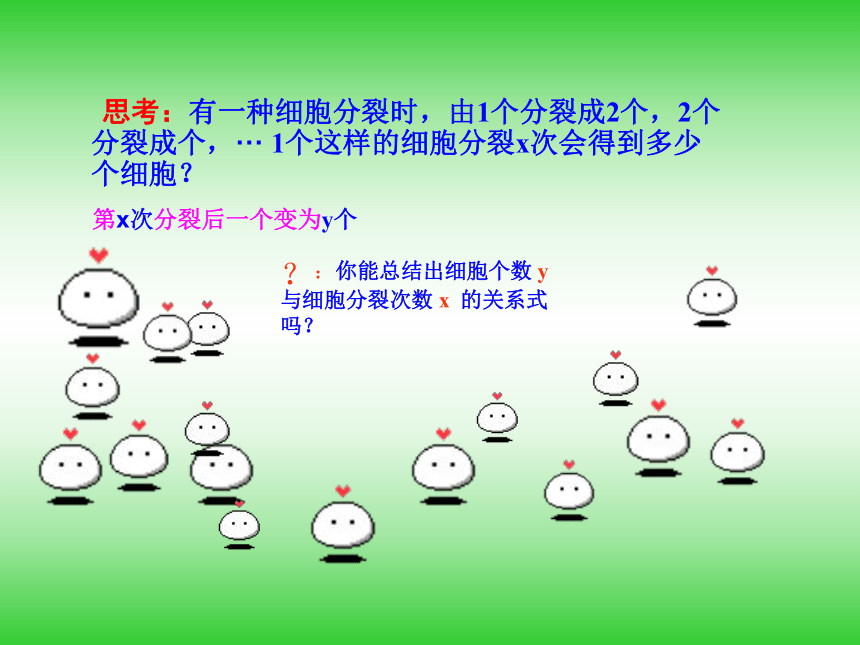
思考:有一种细胞分裂时,由1个分裂成2个,2个分裂成个,··· 1个这样的细胞分裂x次会得到多少个细胞??:你能总结出细胞个数 y 与细胞分裂次数 x 的关系式吗?第x次分裂后一个变为y个 思考: 有一种细胞分裂时,由1个分裂成2个,2个分裂成4个,··· 1个这样的细胞分裂x次会得到多少个细胞?解:细胞个数y与细胞
分裂次数x的关系式是 y=2x,思考3:上述函数在其结构上有何共同特点? 思考5:指数函数y=ax(a>0,a≠1)的定义域是什么? 思考1:我们研究函数的性质,通常都研究哪几个性质?提示:函数的三要素:定义域、对应关系和值域;
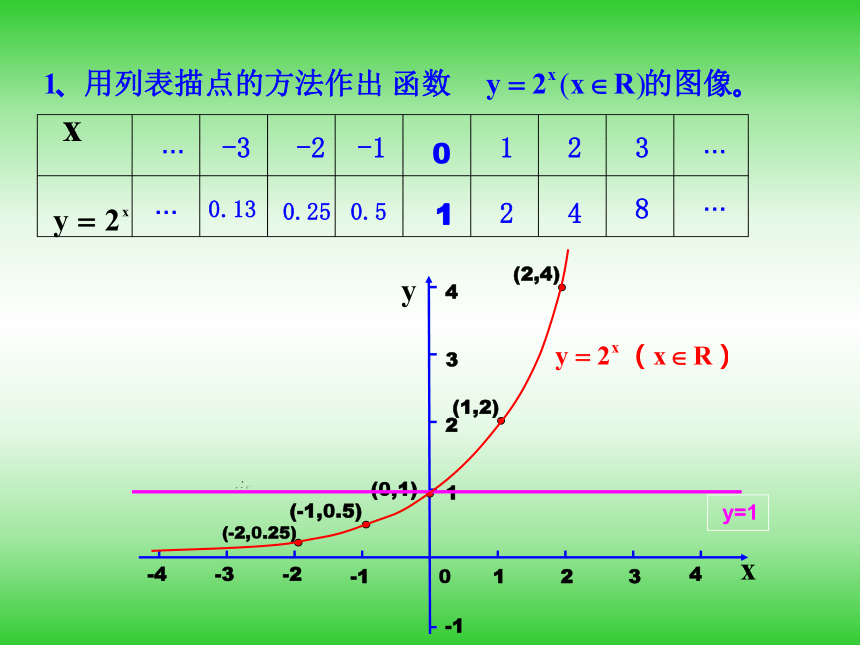
函数的基本性质:单调性和奇偶性.知识探究(二):指数函数的图象与性质 y=1两函数图象有
什么共同点,
又有什么不同
特征?影响函数图象
特征的主要因
素是什么?指数函数的图象和性质R(0,+∞)(0,1)01增函数减函数理论迁移考点一: 指数函数的概念[例1] 给出下列函数:
①y=2·3x;②y=3x+1;③y=3x;④y=x3;⑤y=(-2)x.
其中,指数函数的个数是 ( )
A.0 B.1 C.2 D.3
[精解详析] ①中,3x的系数是2,故①不是指数函数;
②中,y=3x+1的指数是x+1,不是自变量x,故②不是指数函数;
③中,3x的系数是1,幂的指数是自变量x,且只有3x一项,故③是指数函数;④中,y=x3的底为自变量,指数为常数,故④不是指数函数.
⑤中,底数-2<0,不是指数函数,所以只有③是指数函数.
[答案] B[一点通] 判断一个函数是否为指数函数,只需判定其解析式是否符合y=ax(a>0且a≠1)这一形式,即底数a为不等于1的正常数,指数只能是x,且ax的系数为1.1.函数y=(a2-3a+3)ax是指数函数,则a的值为______.答案:2考点二: 指数函数的图象问题[一点通] 1.指数函数的图象随底数变化的规律
(1)无论指数函数的底数a如何变化,指数函数y=ax的图象都与直线x=1相交于点(1,a).由图象可知:在y轴右侧,图象从下到上相应的底数由小变大.
(2)指数函数的底数与图象间的关系可概括为:在第一象限内,图高则底大.2.指数函数图象问题的处理方法
(1)抓住图象上的特殊点,如指数函数的图象过定点(0,1);
(2)利用图象变换,如函数图象的平移变换(左右平移、上下平移);
(3)利用函数的奇偶性与单调性.3.函数y=2-|x|的大致图象是 ( )答案:C4.若函数y=ax+b-1(a>0,且a≠1)的图象经过第二、三、
四象限,则一定有 ( )
A.00 B.a>1,且b>0
C.00解析:根据题意画出函数y=ax+b-1(a>0,且a≠1)的大致图象,如图所示,所以0答案:C考点三: 与指数函数有关的定义域、值域问题[一点通] 函数y=af(x)的定义域、值域的求法
(1)函数y=af(x)的定义域与y=f(x)的定义域相同.
(2)函数y=af(x)的值域的求法如下:
①换元,令t=f(x);
②求t=f(x)的定义域D;?
③求t=f(x)的值域M;
④利用y=at的单调性求y=at,t∈M的值域.解析:由题意知ax≥1的解集是(-∞,0],∴0答案:(0,1)1.应用指数函数y=ax的单调性时,如果底数a大小不确定,必须分“a>1”和“02.当a>1时,a的值越大,图象越靠近y轴,递增速度越快.当0
思考:有一种细胞分裂时,由1个分裂成2个,2个分裂成个,··· 1个这样的细胞分裂x次会得到多少个细胞??:你能总结出细胞个数 y 与细胞分裂次数 x 的关系式吗?第x次分裂后一个变为y个 思考: 有一种细胞分裂时,由1个分裂成2个,2个分裂成4个,··· 1个这样的细胞分裂x次会得到多少个细胞?解:细胞个数y与细胞
分裂次数x的关系式是 y=2x,思考3:上述函数在其结构上有何共同特点? 思考5:指数函数y=ax(a>0,a≠1)的定义域是什么? 思考1:我们研究函数的性质,通常都研究哪几个性质?提示:函数的三要素:定义域、对应关系和值域;
函数的基本性质:单调性和奇偶性.知识探究(二):指数函数的图象与性质 y=1两函数图象有
什么共同点,
又有什么不同
特征?影响函数图象
特征的主要因
素是什么?指数函数的图象和性质R(0,+∞)(0,1)01增函数减函数理论迁移考点一: 指数函数的概念[例1] 给出下列函数:
①y=2·3x;②y=3x+1;③y=3x;④y=x3;⑤y=(-2)x.
其中,指数函数的个数是 ( )
A.0 B.1 C.2 D.3
[精解详析] ①中,3x的系数是2,故①不是指数函数;
②中,y=3x+1的指数是x+1,不是自变量x,故②不是指数函数;
③中,3x的系数是1,幂的指数是自变量x,且只有3x一项,故③是指数函数;④中,y=x3的底为自变量,指数为常数,故④不是指数函数.
⑤中,底数-2<0,不是指数函数,所以只有③是指数函数.
[答案] B[一点通] 判断一个函数是否为指数函数,只需判定其解析式是否符合y=ax(a>0且a≠1)这一形式,即底数a为不等于1的正常数,指数只能是x,且ax的系数为1.1.函数y=(a2-3a+3)ax是指数函数,则a的值为______.答案:2考点二: 指数函数的图象问题[一点通] 1.指数函数的图象随底数变化的规律
(1)无论指数函数的底数a如何变化,指数函数y=ax的图象都与直线x=1相交于点(1,a).由图象可知:在y轴右侧,图象从下到上相应的底数由小变大.
(2)指数函数的底数与图象间的关系可概括为:在第一象限内,图高则底大.2.指数函数图象问题的处理方法
(1)抓住图象上的特殊点,如指数函数的图象过定点(0,1);
(2)利用图象变换,如函数图象的平移变换(左右平移、上下平移);
(3)利用函数的奇偶性与单调性.3.函数y=2-|x|的大致图象是 ( )答案:C4.若函数y=ax+b-1(a>0,且a≠1)的图象经过第二、三、
四象限,则一定有 ( )
A.0
C.0
(1)函数y=af(x)的定义域与y=f(x)的定义域相同.
(2)函数y=af(x)的值域的求法如下:
①换元,令t=f(x);
②求t=f(x)的定义域D;?
③求t=f(x)的值域M;
④利用y=at的单调性求y=at,t∈M的值域.解析:由题意知ax≥1的解集是(-∞,0],∴0
