高中数学必修一第二章对数函数及其性质
文档属性
| 名称 | 高中数学必修一第二章对数函数及其性质 |  | |
| 格式 | zip | ||
| 文件大小 | 685.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-06 20:27:57 | ||
图片预览






文档简介
课件34张PPT。 2.2.2 对数函数及其性质 第一课时 对数函数及其性质1.用清水漂洗含1个单位质量污垢的衣服,若每次能洗去污垢的四分之三,试写出漂洗次数y与残留污垢x的关系式. 2. (x>0)是函数吗?若是,这是什么
类型的函数?提出问题思考1:在上面的问题中,若要使残留的污垢为原来的
,则要漂洗几次? 思考3:函数 称为对数函数,
一般地,具备什么条件的函数叫对数函数? 知识探究(一):对数函数的概念思考4:为什么在对数函数中要求a>0,且a≠l? 思考5:对数函数的定义域、值域分别是什么?思考6:函数 与 相同吗?
为什么? 思考1:研究对数函数的基本特性应先研究其图象.你有什么方法作对数函数的图象?★在同一坐标系中用描点法画出对数函数
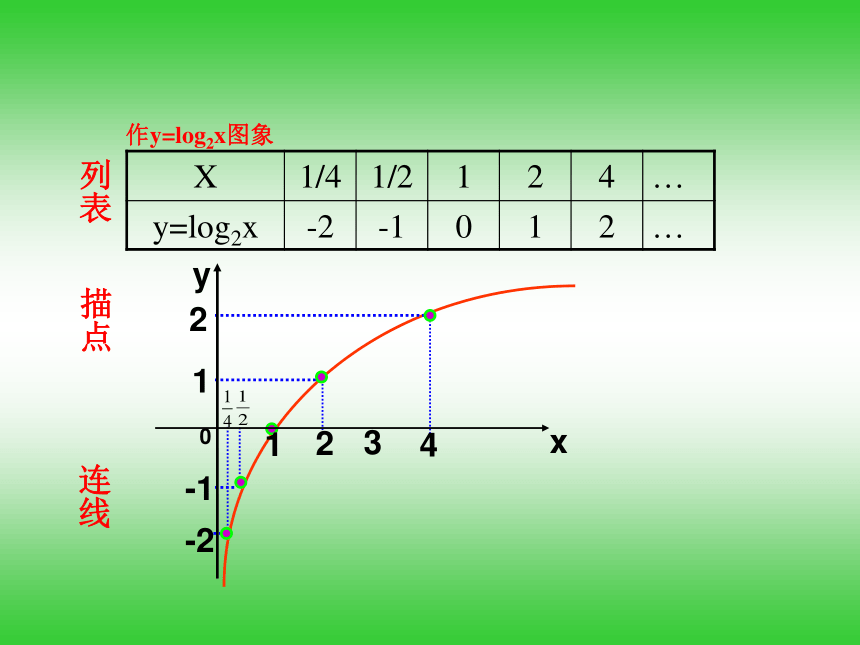
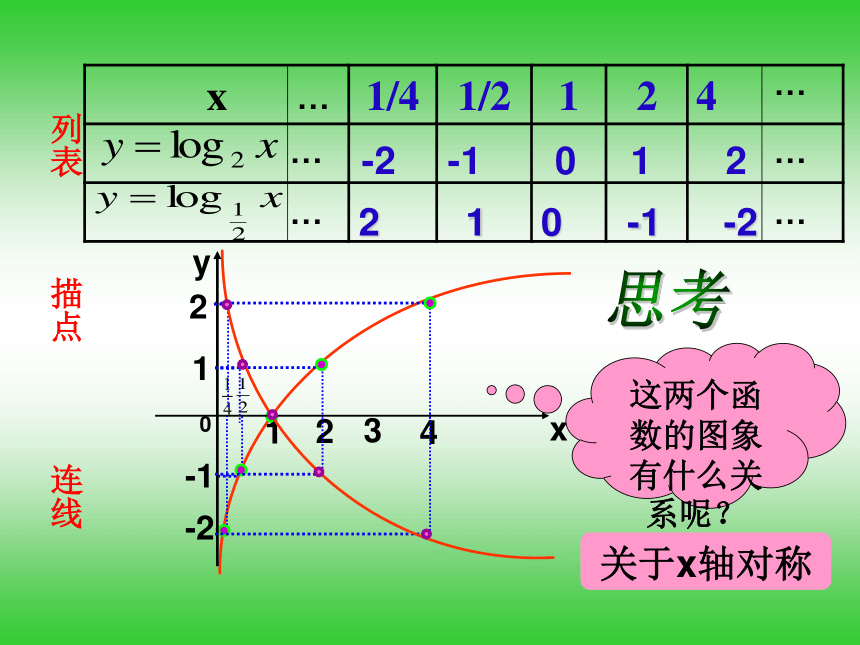
的图象.知识探究(二):对数函数的图象列表描点作y=log2x图象连线列表描点连线 2 1 0 -1 -2 -2 -1 0 1 2 思考这两个函数的图象有什么关系呢?关于x轴对称… … … … … … 定义域 :( 0,+∞) 值 域 :R
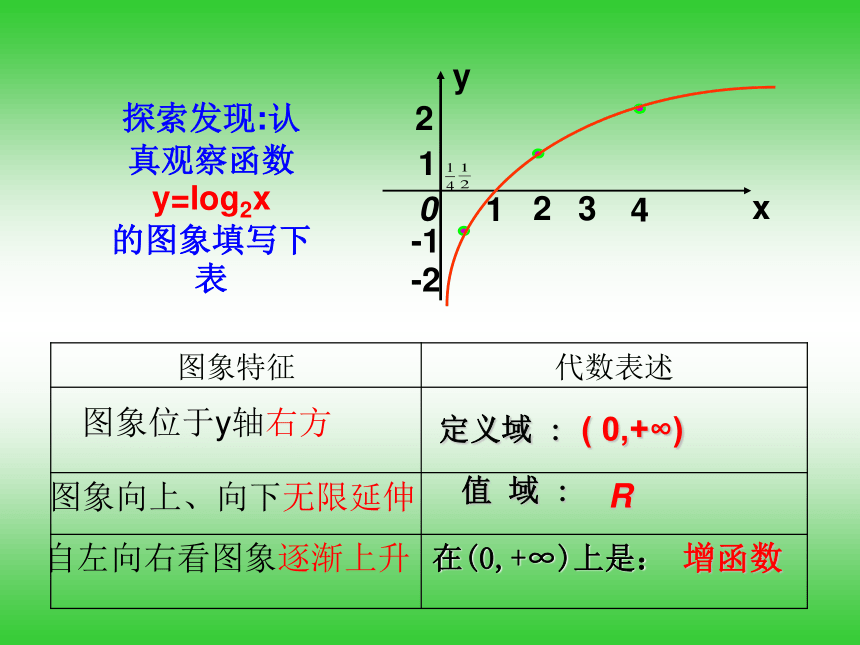
增函数在(0,+∞)上是:探索发现:认真观察函数y=log2x
的图象填写下表图象位于y轴右方图象向上、向下无限延伸自左向右看图象逐渐上升21-1-21240
y x3定义域 :( 0,+∞) 值 域 :R
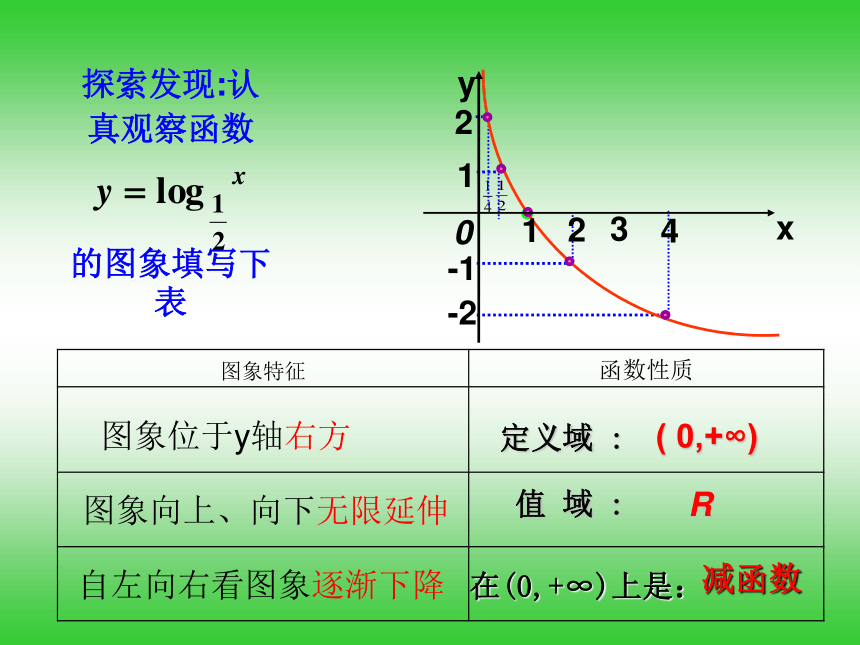
减函数在(0,+∞)上是:图象位于y轴右方图象向上、向下无限延伸自左向右看图象逐渐下降探索发现:认真观察函数
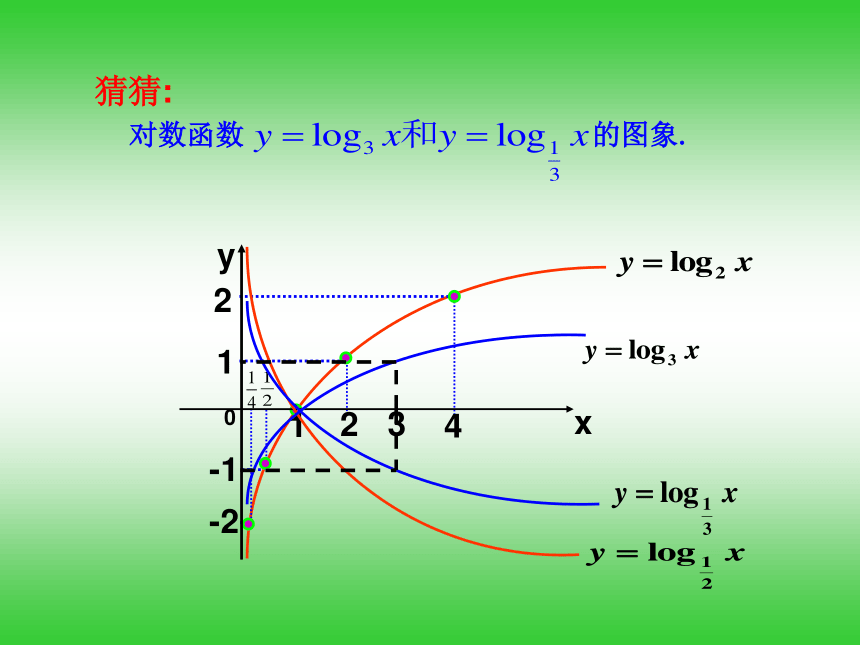
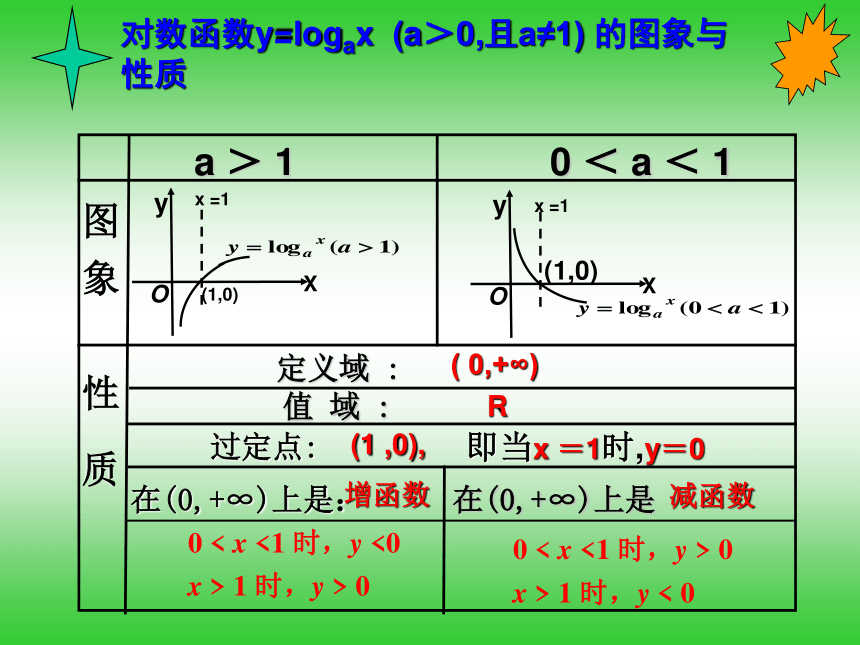
的图象填写下表 对数函数 的图象.猜猜: 图 象 性 质a > 1 0 < a < 1定义域 : 值 域 :过定点:在(0,+∞)上是:在(0,+∞)上是( 0,+∞)R(1 ,0), 即当x =1时,y=0增函数减函数0 < x <1 时,y <0
x > 1 时,y > 0 0 < x <1 时,y > 0
x > 1 时,y < 0 考点一: 求对数函数的定义域理论迁移答案:A答案:B[精解详析] 第一步:作出y=log2x的图象,如图(1).
第二步:将y=log2x的图象在x轴下方的部分以x轴为对称轴翻折到x轴的上方得y=|log2x|的图象,如 图(2).
第三步:将y=|log2x|的图象沿y轴方向向上平移2个单位,得到y=|log2x|+2的图象,如图(3).考点一: 对数函数的图象[一点通] 1.含有绝对值的函数的图象变换是一种对称变换.一般地,y=|f(x)|的图象是保留y=f(x)的图象在x轴上方的部分,并把x轴下方的部分以x轴为对称轴翻折到x轴上方而得到的.
2.y=f(x)的图象与y=f(-x)的图象关于y轴对称,y=f(x)的图象与y=-f(x)的图象关于x轴对称.4.函数y=lg(x+1)的图象大致是( )答案:C答案:A答案:[1,2] [例3](8分)求函数y=log2(x2-4x+6)的值域.
考点一: 对数函数的值域[精解详析]∵x2-4x+6=(x-2)2+2≥2,
又f(x)=log2u在(0,+∞)上是增函数,
∴log2(x2-4x+6)≥log22=1. (6分)
∴函数的值域是[1,+∞). (8分)[一点通]求函数的值域一定要注意定义域对它的影响,然后利用函数的单调性求解.当底数中含有参数时,需要对参数的取值进行讨论.7.函数f(x)=log2(3x+1)的值域为 ( )
A.(0,+∞) B.[0,+∞)
C.(1,+∞) D.[1,+∞)
解析:∵3x>0,∴3x+1>1,∴log2(3x+1)>0.
∴函数f(x)的值域为(0,+∞).
答案:A解:(1)y=log2(x2+4)的定义域为R.
∵x2+4≥4,∴log2(x2+4)≥log24=2.
∴y=log2(x2+4)的值域为{y|y≥2}.1.函数y=logax(a>0且a≠1)的底数变化对图象位置的影响(1)上下比较:在直线x=1的右侧,a>1时,a 越大,图象向右越靠近x轴;0(2)左右比较:比较图象与y=1的交点,交点的横坐标越大,对应的对数函数的底数越大.方法规律小结2.对于对数函数图象性质的助记口诀
对数增减有思路,函数图象看底数.底数只能大于0,等于1来也不行.底数若是大于1,图象逐渐往上升;底数0到1之间,图象逐渐往下降.无论函数增和减,图象都过(1,0)点.同学们 再见!
类型的函数?提出问题思考1:在上面的问题中,若要使残留的污垢为原来的
,则要漂洗几次? 思考3:函数 称为对数函数,
一般地,具备什么条件的函数叫对数函数? 知识探究(一):对数函数的概念思考4:为什么在对数函数中要求a>0,且a≠l? 思考5:对数函数的定义域、值域分别是什么?思考6:函数 与 相同吗?
为什么? 思考1:研究对数函数的基本特性应先研究其图象.你有什么方法作对数函数的图象?★在同一坐标系中用描点法画出对数函数
的图象.知识探究(二):对数函数的图象列表描点作y=log2x图象连线列表描点连线 2 1 0 -1 -2 -2 -1 0 1 2 思考这两个函数的图象有什么关系呢?关于x轴对称… … … … … … 定义域 :( 0,+∞) 值 域 :R
增函数在(0,+∞)上是:探索发现:认真观察函数y=log2x
的图象填写下表图象位于y轴右方图象向上、向下无限延伸自左向右看图象逐渐上升21-1-21240
y x3定义域 :( 0,+∞) 值 域 :R
减函数在(0,+∞)上是:图象位于y轴右方图象向上、向下无限延伸自左向右看图象逐渐下降探索发现:认真观察函数
的图象填写下表 对数函数 的图象.猜猜: 图 象 性 质a > 1 0 < a < 1定义域 : 值 域 :过定点:在(0,+∞)上是:在(0,+∞)上是( 0,+∞)R(1 ,0), 即当x =1时,y=0增函数减函数0 < x <1 时,y <0
x > 1 时,y > 0 0 < x <1 时,y > 0
x > 1 时,y < 0 考点一: 求对数函数的定义域理论迁移答案:A答案:B[精解详析] 第一步:作出y=log2x的图象,如图(1).
第二步:将y=log2x的图象在x轴下方的部分以x轴为对称轴翻折到x轴的上方得y=|log2x|的图象,如 图(2).
第三步:将y=|log2x|的图象沿y轴方向向上平移2个单位,得到y=|log2x|+2的图象,如图(3).考点一: 对数函数的图象[一点通] 1.含有绝对值的函数的图象变换是一种对称变换.一般地,y=|f(x)|的图象是保留y=f(x)的图象在x轴上方的部分,并把x轴下方的部分以x轴为对称轴翻折到x轴上方而得到的.
2.y=f(x)的图象与y=f(-x)的图象关于y轴对称,y=f(x)的图象与y=-f(x)的图象关于x轴对称.4.函数y=lg(x+1)的图象大致是( )答案:C答案:A答案:[1,2] [例3](8分)求函数y=log2(x2-4x+6)的值域.
考点一: 对数函数的值域[精解详析]∵x2-4x+6=(x-2)2+2≥2,
又f(x)=log2u在(0,+∞)上是增函数,
∴log2(x2-4x+6)≥log22=1. (6分)
∴函数的值域是[1,+∞). (8分)[一点通]求函数的值域一定要注意定义域对它的影响,然后利用函数的单调性求解.当底数中含有参数时,需要对参数的取值进行讨论.7.函数f(x)=log2(3x+1)的值域为 ( )
A.(0,+∞) B.[0,+∞)
C.(1,+∞) D.[1,+∞)
解析:∵3x>0,∴3x+1>1,∴log2(3x+1)>0.
∴函数f(x)的值域为(0,+∞).
答案:A解:(1)y=log2(x2+4)的定义域为R.
∵x2+4≥4,∴log2(x2+4)≥log24=2.
∴y=log2(x2+4)的值域为{y|y≥2}.1.函数y=logax(a>0且a≠1)的底数变化对图象位置的影响(1)上下比较:在直线x=1的右侧,a>1时,a 越大,图象向右越靠近x轴;0
对数增减有思路,函数图象看底数.底数只能大于0,等于1来也不行.底数若是大于1,图象逐渐往上升;底数0到1之间,图象逐渐往下降.无论函数增和减,图象都过(1,0)点.同学们 再见!
