高中数学必修一第二章 对数函数及其性质的应用第二课时
文档属性
| 名称 | 高中数学必修一第二章 对数函数及其性质的应用第二课时 |  | |
| 格式 | zip | ||
| 文件大小 | 581.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-06 20:30:41 | ||
图片预览







文档简介
课件27张PPT。 2.2.2 对数函数及其性质 第二课时 对数函数及其性质的应用图 象 性 质a > 1 0 < a < 1定义域 : 值 域 :过定点:在(0,+∞)上是:在(0,+∞)上是对数函数y=logax (a>0,且a≠1) 的图象与性质( 0,+∞)R(1 ,0), 即当x =1时,y=0增函数减函数0 < x <1 时,y <0
x > 1 时,y > 0 0 < x <1 时,y > 0
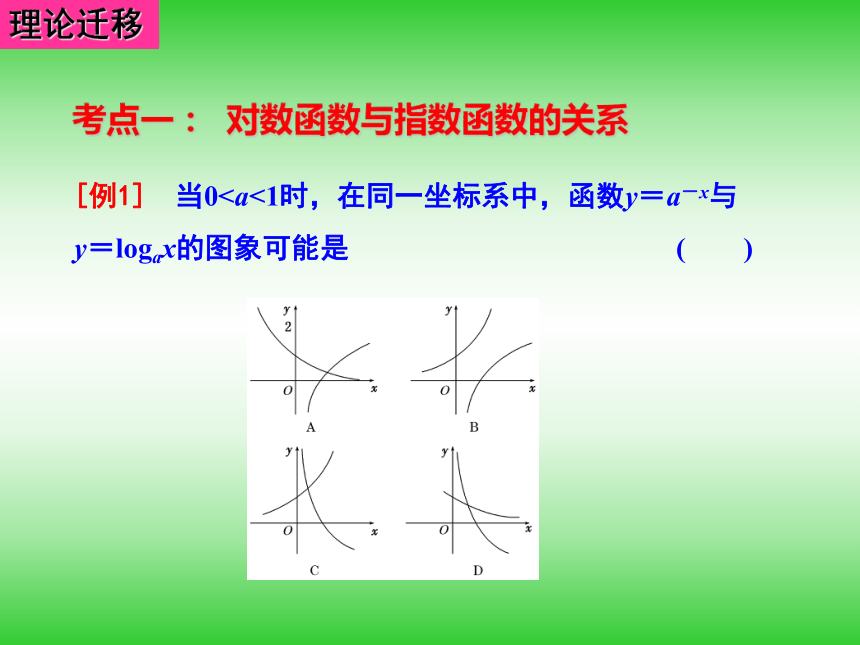
x > 1 时,y < 0 复习回顾[例1] 当0y=logax的图象可能是 ( )考点一: 对数函数与指数函数的关系理论迁移[精解详析] 当01,因此y=a-x=(a-1)x
为增函数且图像过(0,1),y=logax为减函数且图像过
(1,0),显然只有C符合.
[答案] C[一点通] 解决这类题型的办法有直接法与排除法.直接法一般是借助函数的定义域、奇偶性、单调性、过定点等特征对函数的图象进行分析进而得解的方法.排除法通常是利用函数的定义域以及图象经过的一些特殊点进行验证的方法.1.已知函数f(x)=ax(a>0,a≠1)的反函数为g(x),且满足
g(2)<0,则函数g(x+1)的图象是下图中的 ( )解析:由y=ax解得x=logay,
∴g(x)=logax.
又∵g(2)<0,∴0故g(x+1)=loga(x+1)是单调递减的,并且图像是由函数g(x)=logax的图像向左平移1个单位得到的.
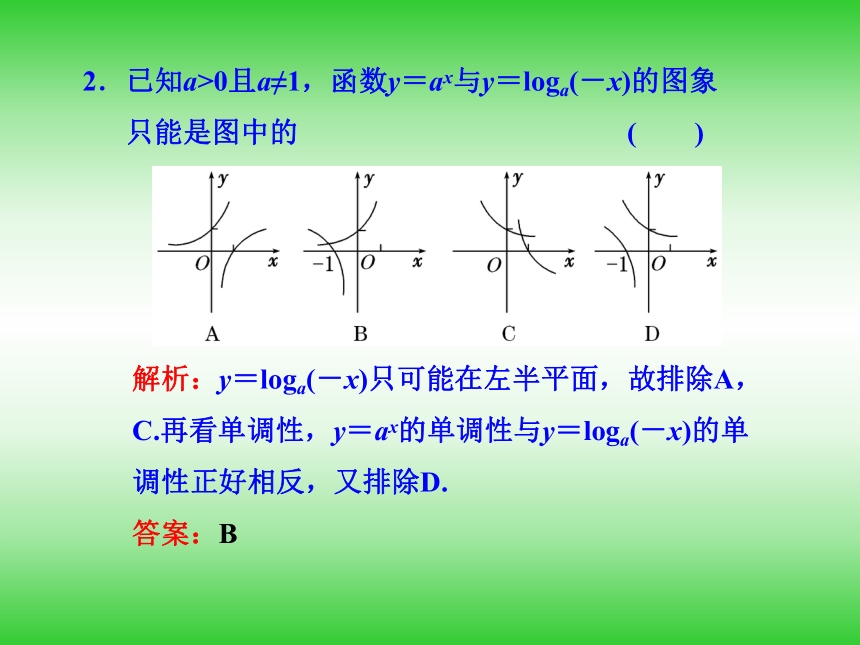
答案:A2.已知a>0且a≠1,函数y=ax与y=loga(-x)的图象
只能是图中的 ( )解析:y=loga(-x)只可能在左半平面,故排除A,C.再看单调性,y=ax的单调性与y=loga(-x)的单调性正好相反,又排除D.
答案:B [例2] 比较下列各组数的大小:
(1)log2π与log20.9;
(2)log20.3与log0.20.3;
(3)log0.76,0.76与60.7;
(4)log20.4,log30.4.
考点二: 比较大小问题[精解详析] (1)因为函数y=log2x在(0,+∞)上 是增函数,π>0.9,所以log2π>log20.9.
(2)因为log20.3log0.21=0,
所以log20.3(3)因为60.7>60=1,0<0.76<0.70=1,
又log0.760.76>log0.76.(4)底数不同,但真数相同.根据y=logax的图象在a>1,0log20.4.[一点通] 利用函数的单调性可进行对数大小的比较,常用的方法有
(1)同底数的两个对数值的大小比较,由对数函数的单调性比较.
(2)底数不同且真数也不相同的两个对数值的大小比较,常用引入中间变量法比较,通常取中间量为-1,0,1等.(3)底数不同而真数相同的两个对数值的大小比较,常用数形结合思想来解决,也可用换底公式化为同底,再进行比较.3.若a=log0.23,b=log0.2e,c=log0.20.3,则 ( )
A.a>b>c B.aC.a>c>b D.c>a>b解析:∵0.3b>a.
答案:B答案:C (4)当a>1时,y=logax在(0,+∞)上单调递增,
∴loga3 当0 ∴loga3>loga10.考点三: 对数函数单调性的应用[一点通] 1.求形如y=logaf(x)的函数的单调区间一般
有如下几个步骤:
(1)求出函数的定义域;
(2)研究函数t=f(x)和函数y=logat在定义域上的单调性;
(3)判断出函数的增减性求出单调区间.2.函数y=f[g(x)]的里层函数μ=g(x)与外层函数
y=f(μ)单调性之间的关系见下表:可简记为“同增异减”.解析:f(x)的图象如图所示,由图象可知单调递增区间为[1,+∞).答案:D答案:B8.解不等式log2(x+5)>log2(3-x).方法规律小结1.利用对数函数的图象与性质可以比较对数的大小,求有关函数的单调区间,解简单的不等式等.
2.解决与对数函数有关的问题,首先要考虑函数的定义域,其次要考虑底数的范围.若底数中含有参数,要对底数进行讨论.同学们 再见!
x > 1 时,y > 0 0 < x <1 时,y > 0
x > 1 时,y < 0 复习回顾[例1] 当0
为增函数且图像过(0,1),y=logax为减函数且图像过
(1,0),显然只有C符合.
[答案] C[一点通] 解决这类题型的办法有直接法与排除法.直接法一般是借助函数的定义域、奇偶性、单调性、过定点等特征对函数的图象进行分析进而得解的方法.排除法通常是利用函数的定义域以及图象经过的一些特殊点进行验证的方法.1.已知函数f(x)=ax(a>0,a≠1)的反函数为g(x),且满足
g(2)<0,则函数g(x+1)的图象是下图中的 ( )解析:由y=ax解得x=logay,
∴g(x)=logax.
又∵g(2)<0,∴0
答案:A2.已知a>0且a≠1,函数y=ax与y=loga(-x)的图象
只能是图中的 ( )解析:y=loga(-x)只可能在左半平面,故排除A,C.再看单调性,y=ax的单调性与y=loga(-x)的单调性正好相反,又排除D.
答案:B [例2] 比较下列各组数的大小:
(1)log2π与log20.9;
(2)log20.3与log0.20.3;
(3)log0.76,0.76与60.7;
(4)log20.4,log30.4.
考点二: 比较大小问题[精解详析] (1)因为函数y=log2x在(0,+∞)上 是增函数,π>0.9,所以log2π>log20.9.
(2)因为log20.3
所以log20.3
又log0.76
(1)同底数的两个对数值的大小比较,由对数函数的单调性比较.
(2)底数不同且真数也不相同的两个对数值的大小比较,常用引入中间变量法比较,通常取中间量为-1,0,1等.(3)底数不同而真数相同的两个对数值的大小比较,常用数形结合思想来解决,也可用换底公式化为同底,再进行比较.3.若a=log0.23,b=log0.2e,c=log0.20.3,则 ( )
A.a>b>c B.a
答案:B答案:C (4)当a>1时,y=logax在(0,+∞)上单调递增,
∴loga3
有如下几个步骤:
(1)求出函数的定义域;
(2)研究函数t=f(x)和函数y=logat在定义域上的单调性;
(3)判断出函数的增减性求出单调区间.2.函数y=f[g(x)]的里层函数μ=g(x)与外层函数
y=f(μ)单调性之间的关系见下表:可简记为“同增异减”.解析:f(x)的图象如图所示,由图象可知单调递增区间为[1,+∞).答案:D答案:B8.解不等式log2(x+5)>log2(3-x).方法规律小结1.利用对数函数的图象与性质可以比较对数的大小,求有关函数的单调区间,解简单的不等式等.
2.解决与对数函数有关的问题,首先要考虑函数的定义域,其次要考虑底数的范围.若底数中含有参数,要对底数进行讨论.同学们 再见!
