高中数学必修一第三章 函数的零点与方程的根
文档属性
| 名称 | 高中数学必修一第三章 函数的零点与方程的根 |

|
|
| 格式 | zip | ||
| 文件大小 | 525.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-06 00:00:00 | ||
图片预览







文档简介
(共32张PPT)
3.1.1 函数与方程
3.1.1 函数的零点与方程的根
1.对于数学关系式:2x-1=0与y=2x-1它们的含义分别如何?
2.方程 2x-1=0的根与函数y=2x-1的图象有什么关系?
3.我们如何对方程f(x)=0的根与函数y=f(x)的图象的关系作进一步阐述?
提出问题
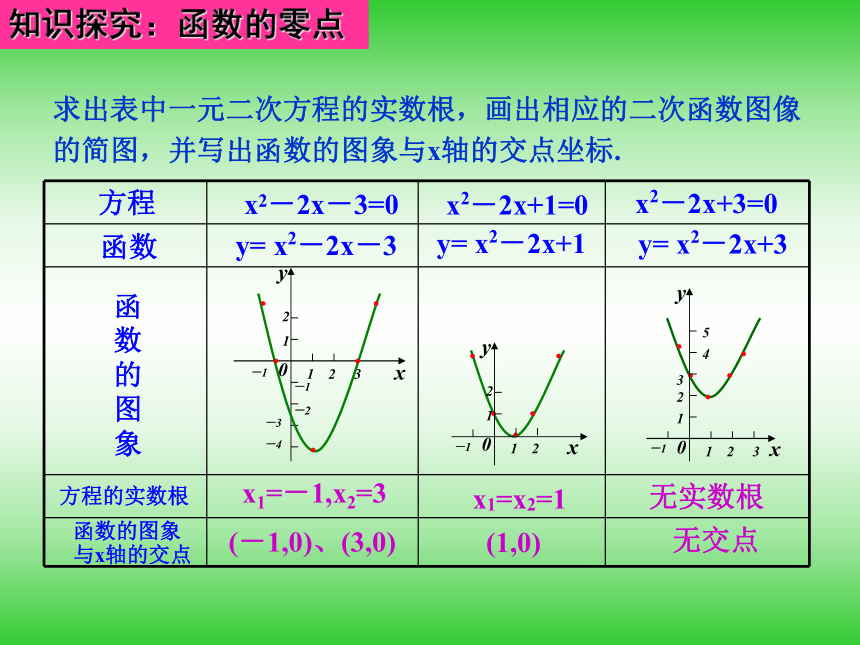
方程
x2-2x+1=0
x2-2x+3=0
y= x2-2x-3
y= x2-2x+1
函数
函
数
的
图
象
方程的实数根
x1=-1,x2=3
x1=x2=1
无实数根
函数的图象
与x轴的交点
(-1,0)、(3,0)
(1,0)
无交点
x2-2x-3=0
x
y
0
-1
3
2
1
1
2
-1
-2
-3
-4
.
.
.
.
.
.
.
.
.
.
x
y
0
-1
3
2
1
1
2
5
4
3
.
.
.
.
.
y
x
0
-1
2
1
1
2
y= x2-2x+3
求出表中一元二次方程的实数根,画出相应的二次函数图像的简图,并写出函数的图象与x轴的交点坐标.
知识探究:函数的零点
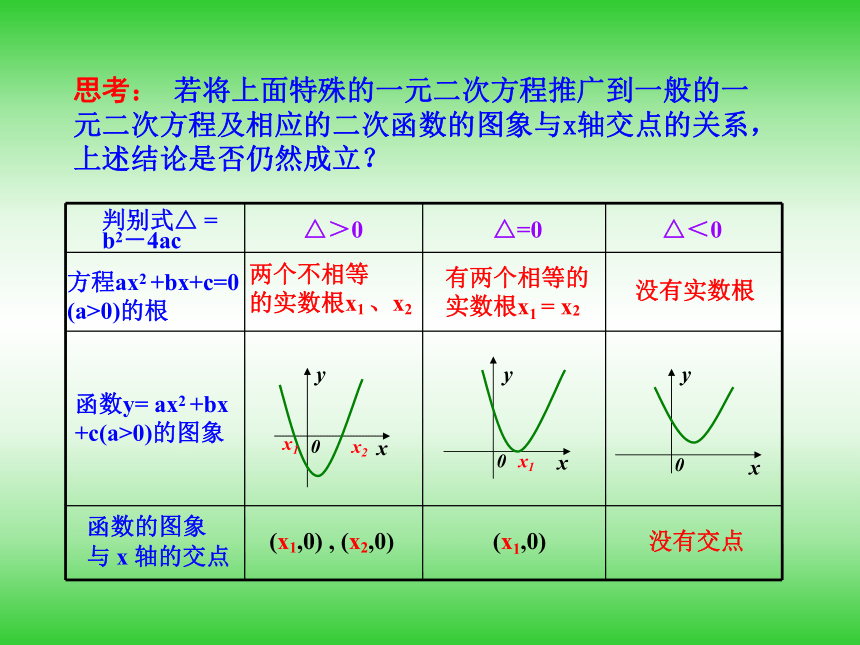
方程ax2 +bx+c=0
(a>0)的根
函数y= ax2 +bx
+c(a>0)的图象
判别式△ =
b2-4ac
△>0
△=0
△<0
函数的图象
与 x 轴的交点
有两个相等的
实数根x1 = x2
没有实数根
x
y
x1
x2
0
x
y
0
x1
x
y
0
(x1,0) , (x2,0)
(x1,0)
没有交点
两个不相等
的实数根x1 、x2
思考: 若将上面特殊的一元二次方程推广到一般的一元二次方程及相应的二次函数的图象与x轴交点的关系,上述结论是否仍然成立?
对于函数y=f(x), 叫做函数
y=f(x)的零点。
方程f(x)=0有实数根
函数y=f(x)的图象与x轴有交点
函数y=f(x)有零点
函数的零点定义:
等价关系
使f(x)=0的实数x
零点的求法
代数法
图像法
求下列函数的零点
6
5
)
(
2
+
-
=
x
x
x
f
1
2
)
(
-
=
x
x
f
(1)
(2)
2和3
0
提示:求函数零点的步骤:
(1)令f(x)=0;
(2)解方程f(x)=0;
(3)写出零点
思考1:求函数零点的步骤是什么?
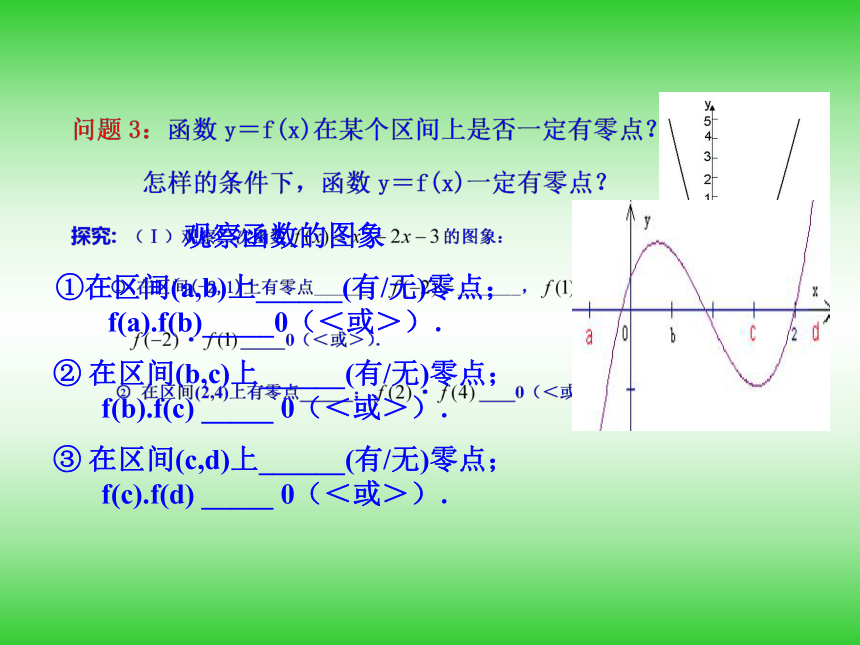
观察函数的图象
①在区间(a,b)上______(有/无)零点;f(a).f(b)_____0(<或>).
② 在区间(b,c)上______(有/无)零点;f(b).f(c) _____ 0(<或>).
③ 在区间(c,d)上______(有/无)零点;f(c).f(d) _____ 0(<或>).
x
y
0
0
y
x
0
y
x
0
y
x
x
y
0
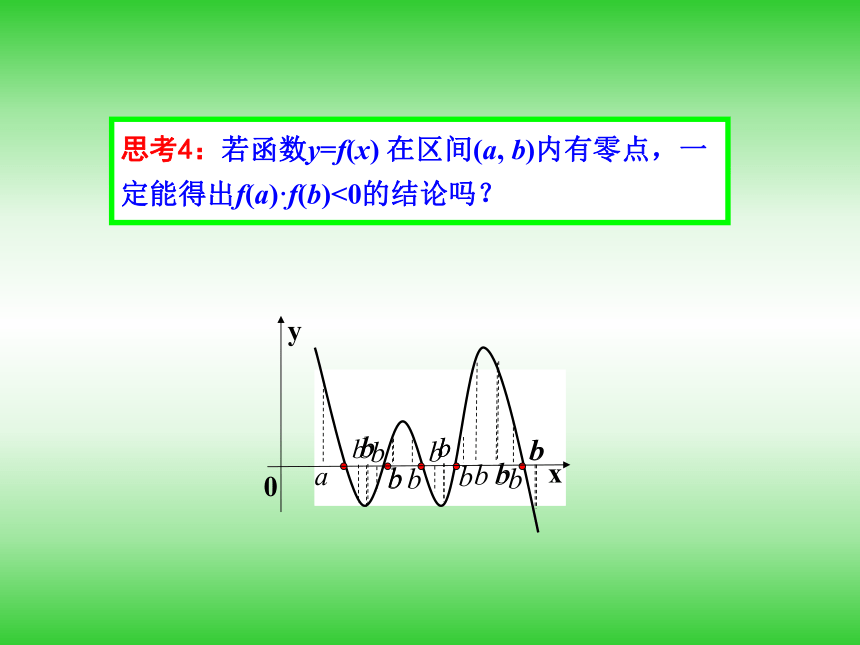
思考4:若函数y=f(x) 在区间(a, b)内有零点,一定能得出f(a)·f(b)<0的结论吗?
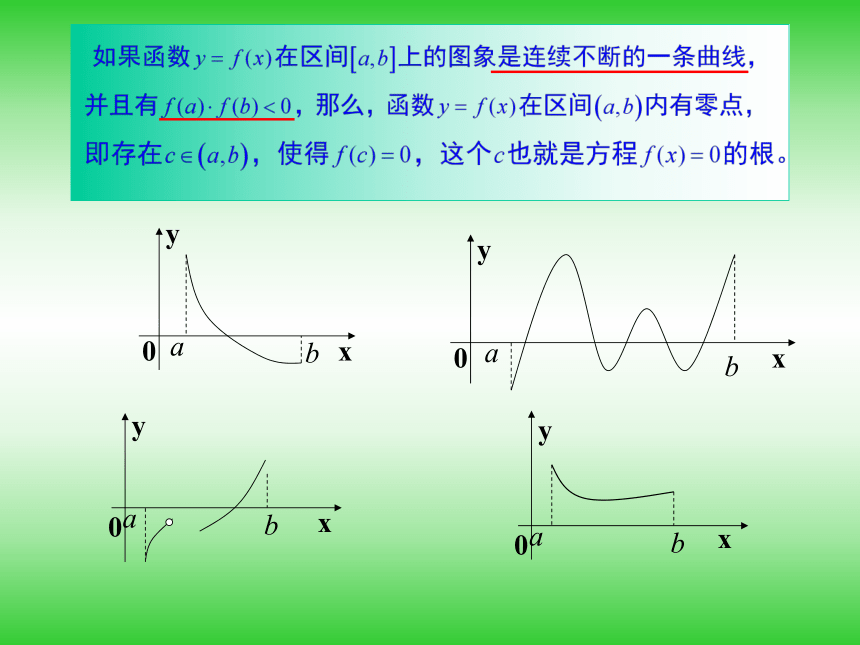
如果函数 y=f(x) 在[a,b]上,图象是连续的,并且在闭区间的两个端点上的函数值互异,即f(a)f(b)﹤0,且是单调函数那么,这个函数在(a,b)内必有惟一的一个零点.
定理:
考点一: 求函数的零点
理论迁移
[例1] 求下列函数的零点:
(1)f(x)=-x2-2x+3; (2)f(x)=x4-1.
[精解详析] (1)∵f(x)=-x2-2x+3
=-(x+3)(x-1),
∴方程-x2-2x+3=0的两根分别是-3和1.
故函数的零点是-3,1.
(2)∵f(x)=x4-1=(x2+1)(x+1)(x-1),
∴方程x4-1=0的实数根是-1或1.
故函数的零点是-1,1.
[一点通] 函数零点的求法
(1)代数法:求方程f(x)=0的实数根;
(2)几何法:对于不能用求根公式求根的方程f(x)=0,可以将它与函数y=f(x)的图象联系起来,图象与x轴的交点的横坐标即为函数的零点.
1.若f(x)=ax-b(b≠0)有一个零点3,则函数g(x)=
bx2+3ax的零点是________.
解析:∵f(x)=ax-b的零点是3,
∴f(3)=0,即3a-b=0,也就是b=3a.
∴g(x)=bx2+3ax=bx2+bx=bx(x+1).
∴g(x)的零点为-1,0.
答案:-1,0
2.若函数f(x)=x2+ax+b的零点是2和-4,求a、b的值.
3.求下列函数的零点:
(1)f(x)=2x-1;
(2)f(x)=2x2+4x+2;
(3)f(x)=x3-2x2-3x.
解:(1)令f(x)=0,
即2x-1=0,2x=1.
∴x=0.∴f(x)有一个零点0.
(2)令f(x)=0,
即2x2+4x+2=0,x2+2x+1=0.
∴x=-1.∴f(x)有一个零点-1.
(3)令f(x)=0,即x3-2x2-3x=0,
x(x2-2x-3)=0,x(x-3)(x+1)=0,
∴x1=-1,x2=0,x3=3.
∴f(x)有三个零点-1,0,3.
[精解详析] (1)令f(x)=0,
即x2-7x+12=0,得
Δ=49-4×12=1>0,
∴方程x2-7x+12=0有两个不相等的实数根3,4.
∴函数f(x)有两个零点,分别是3,4.
考点二: 函数零点的判断
[一点通] 判断函数零点个数的主要方法
(1)转化为解方程,有几个根就有几个零点.
(2)画出函数y=f(x)的图象,判定它与x轴的交点个数,从而判定零点的个数.
(3)结合单调性,利用f(a)·f(b)的符号,可判定y=f(x)
在(a,b)上零点的个数.
(4)转化成两个函数图象的交点问题.
答案:D
5.函数f(x)=2x+3x的零点所在的一个区间是( )
A.(-2,-1) B.(-1,0)
C.(0,1) D.(1,2)
答案:B
答案:0
[例3] (10分)已知关于x的二次方程ax2-2(a+1)x+a-1=0有两根,且一根大于2,另一根小于2,试求实数a的取值范围.
考点三: 函数零点的应用
[精解详析] 令f(x)=ax2-2(a+1)x+a-1,依题意知,函数f(x)有两个零点,且一零点大于2,一零点小于2.
∴f(x)的图象大致如图所示:
(4分)
[一点通] 解决此类问题可设出方程对应的函数,根据函数的零点所在的区间分析区间端点函数值的符号,建立不等式,使问题得解.当函数解析式中含有参数时,要注意分类讨论.
7.若函数y=x2+(m-2)x-5-m有两个小于2
的零点,则m的取值范围是 ( )
A.(5,+∞) B.(2,+∞)
C.(-∞,2) D.(2,5)
答案:A
8.若f(x)=x+b的零点在区间(0,1)内,则b的取值范
围为________.
答案:(-1,0)
9.若函数f(x)=ax-x-a(a>0,且a≠1)有两个零点,则实
数a的取值范围是________.
解析:函数f(x)=ax-x-a(a>0,且a≠1)有两个零点,就是函数y=ax(a>0且a≠1)与函数y=x+a的图象有两个交点.由图象可知:当01时,函数y=ax(a>1)的图象过点(0,1),当直线y=x+a与y轴的交点(0,a)在(0,1)的上方时一定有两个交点,所以a>1.
答案:(1,+∞)
方法规律小结
1.判断函数y=f(x)零点存在性的两个条件
(1)函数的图象在区间[a,b]上是一条连续不断的曲线;
(2)f(a)·f(b)<0.
2.应用时应注意的问题
(1)并非函数所有的零点都能用这种方法找到,如y=x2的零点就不能用这种方法找到.只有函数值在零点的左右两侧异号时,才能用这种方法.
(2)利用上述结论只能判别函数y=f(x)在区间(a,b)上零点的存在性,但不能确定其零点的个数.
同学们 再见!
3.1.1 函数与方程
3.1.1 函数的零点与方程的根
1.对于数学关系式:2x-1=0与y=2x-1它们的含义分别如何?
2.方程 2x-1=0的根与函数y=2x-1的图象有什么关系?
3.我们如何对方程f(x)=0的根与函数y=f(x)的图象的关系作进一步阐述?
提出问题
方程
x2-2x+1=0
x2-2x+3=0
y= x2-2x-3
y= x2-2x+1
函数
函
数
的
图
象
方程的实数根
x1=-1,x2=3
x1=x2=1
无实数根
函数的图象
与x轴的交点
(-1,0)、(3,0)
(1,0)
无交点
x2-2x-3=0
x
y
0
-1
3
2
1
1
2
-1
-2
-3
-4
.
.
.
.
.
.
.
.
.
.
x
y
0
-1
3
2
1
1
2
5
4
3
.
.
.
.
.
y
x
0
-1
2
1
1
2
y= x2-2x+3
求出表中一元二次方程的实数根,画出相应的二次函数图像的简图,并写出函数的图象与x轴的交点坐标.
知识探究:函数的零点
方程ax2 +bx+c=0
(a>0)的根
函数y= ax2 +bx
+c(a>0)的图象
判别式△ =
b2-4ac
△>0
△=0
△<0
函数的图象
与 x 轴的交点
有两个相等的
实数根x1 = x2
没有实数根
x
y
x1
x2
0
x
y
0
x1
x
y
0
(x1,0) , (x2,0)
(x1,0)
没有交点
两个不相等
的实数根x1 、x2
思考: 若将上面特殊的一元二次方程推广到一般的一元二次方程及相应的二次函数的图象与x轴交点的关系,上述结论是否仍然成立?
对于函数y=f(x), 叫做函数
y=f(x)的零点。
方程f(x)=0有实数根
函数y=f(x)的图象与x轴有交点
函数y=f(x)有零点
函数的零点定义:
等价关系
使f(x)=0的实数x
零点的求法
代数法
图像法
求下列函数的零点
6
5
)
(
2
+
-
=
x
x
x
f
1
2
)
(
-
=
x
x
f
(1)
(2)
2和3
0
提示:求函数零点的步骤:
(1)令f(x)=0;
(2)解方程f(x)=0;
(3)写出零点
思考1:求函数零点的步骤是什么?
观察函数的图象
①在区间(a,b)上______(有/无)零点;f(a).f(b)_____0(<或>).
② 在区间(b,c)上______(有/无)零点;f(b).f(c) _____ 0(<或>).
③ 在区间(c,d)上______(有/无)零点;f(c).f(d) _____ 0(<或>).
x
y
0
0
y
x
0
y
x
0
y
x
x
y
0
思考4:若函数y=f(x) 在区间(a, b)内有零点,一定能得出f(a)·f(b)<0的结论吗?
如果函数 y=f(x) 在[a,b]上,图象是连续的,并且在闭区间的两个端点上的函数值互异,即f(a)f(b)﹤0,且是单调函数那么,这个函数在(a,b)内必有惟一的一个零点.
定理:
考点一: 求函数的零点
理论迁移
[例1] 求下列函数的零点:
(1)f(x)=-x2-2x+3; (2)f(x)=x4-1.
[精解详析] (1)∵f(x)=-x2-2x+3
=-(x+3)(x-1),
∴方程-x2-2x+3=0的两根分别是-3和1.
故函数的零点是-3,1.
(2)∵f(x)=x4-1=(x2+1)(x+1)(x-1),
∴方程x4-1=0的实数根是-1或1.
故函数的零点是-1,1.
[一点通] 函数零点的求法
(1)代数法:求方程f(x)=0的实数根;
(2)几何法:对于不能用求根公式求根的方程f(x)=0,可以将它与函数y=f(x)的图象联系起来,图象与x轴的交点的横坐标即为函数的零点.
1.若f(x)=ax-b(b≠0)有一个零点3,则函数g(x)=
bx2+3ax的零点是________.
解析:∵f(x)=ax-b的零点是3,
∴f(3)=0,即3a-b=0,也就是b=3a.
∴g(x)=bx2+3ax=bx2+bx=bx(x+1).
∴g(x)的零点为-1,0.
答案:-1,0
2.若函数f(x)=x2+ax+b的零点是2和-4,求a、b的值.
3.求下列函数的零点:
(1)f(x)=2x-1;
(2)f(x)=2x2+4x+2;
(3)f(x)=x3-2x2-3x.
解:(1)令f(x)=0,
即2x-1=0,2x=1.
∴x=0.∴f(x)有一个零点0.
(2)令f(x)=0,
即2x2+4x+2=0,x2+2x+1=0.
∴x=-1.∴f(x)有一个零点-1.
(3)令f(x)=0,即x3-2x2-3x=0,
x(x2-2x-3)=0,x(x-3)(x+1)=0,
∴x1=-1,x2=0,x3=3.
∴f(x)有三个零点-1,0,3.
[精解详析] (1)令f(x)=0,
即x2-7x+12=0,得
Δ=49-4×12=1>0,
∴方程x2-7x+12=0有两个不相等的实数根3,4.
∴函数f(x)有两个零点,分别是3,4.
考点二: 函数零点的判断
[一点通] 判断函数零点个数的主要方法
(1)转化为解方程,有几个根就有几个零点.
(2)画出函数y=f(x)的图象,判定它与x轴的交点个数,从而判定零点的个数.
(3)结合单调性,利用f(a)·f(b)的符号,可判定y=f(x)
在(a,b)上零点的个数.
(4)转化成两个函数图象的交点问题.
答案:D
5.函数f(x)=2x+3x的零点所在的一个区间是( )
A.(-2,-1) B.(-1,0)
C.(0,1) D.(1,2)
答案:B
答案:0
[例3] (10分)已知关于x的二次方程ax2-2(a+1)x+a-1=0有两根,且一根大于2,另一根小于2,试求实数a的取值范围.
考点三: 函数零点的应用
[精解详析] 令f(x)=ax2-2(a+1)x+a-1,依题意知,函数f(x)有两个零点,且一零点大于2,一零点小于2.
∴f(x)的图象大致如图所示:
(4分)
[一点通] 解决此类问题可设出方程对应的函数,根据函数的零点所在的区间分析区间端点函数值的符号,建立不等式,使问题得解.当函数解析式中含有参数时,要注意分类讨论.
7.若函数y=x2+(m-2)x-5-m有两个小于2
的零点,则m的取值范围是 ( )
A.(5,+∞) B.(2,+∞)
C.(-∞,2) D.(2,5)
答案:A
8.若f(x)=x+b的零点在区间(0,1)内,则b的取值范
围为________.
答案:(-1,0)
9.若函数f(x)=ax-x-a(a>0,且a≠1)有两个零点,则实
数a的取值范围是________.
解析:函数f(x)=ax-x-a(a>0,且a≠1)有两个零点,就是函数y=ax(a>0且a≠1)与函数y=x+a的图象有两个交点.由图象可知:当0
答案:(1,+∞)
方法规律小结
1.判断函数y=f(x)零点存在性的两个条件
(1)函数的图象在区间[a,b]上是一条连续不断的曲线;
(2)f(a)·f(b)<0.
2.应用时应注意的问题
(1)并非函数所有的零点都能用这种方法找到,如y=x2的零点就不能用这种方法找到.只有函数值在零点的左右两侧异号时,才能用这种方法.
(2)利用上述结论只能判别函数y=f(x)在区间(a,b)上零点的存在性,但不能确定其零点的个数.
同学们 再见!
