高中数学必修一第三章几类不同增长的函数模型
文档属性
| 名称 | 高中数学必修一第三章几类不同增长的函数模型 |

|
|
| 格式 | zip | ||
| 文件大小 | 371.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-06 00:00:00 | ||
图片预览










文档简介
课件37张PPT。 3.2.1 几类不同增长的函数模型1.函数来源于实际又服务于实际,客观世界的变化规律,常需要不同的数学模型来描述,这涉及到函数的应用问题.2.所谓“模型”,通俗的解释就是一种固定的模式或类型,在现代社会中,我们经常用函数模型来解决实际问题.那么,面对一个实际问题,我们怎样选择一个恰当的模型来刻画它呢?提出问题考察下列问题:
假设你有一笔资金用于投资, 现有三种投资方案供你选择,这三种方案的回报如下:
方案一: 每天回报40元;
方案二: 第一天回报10元, 以后每天比前一天多回报10元;
方案三: 第一天回报0.4元, 以后每天的回报比前一天翻一番.
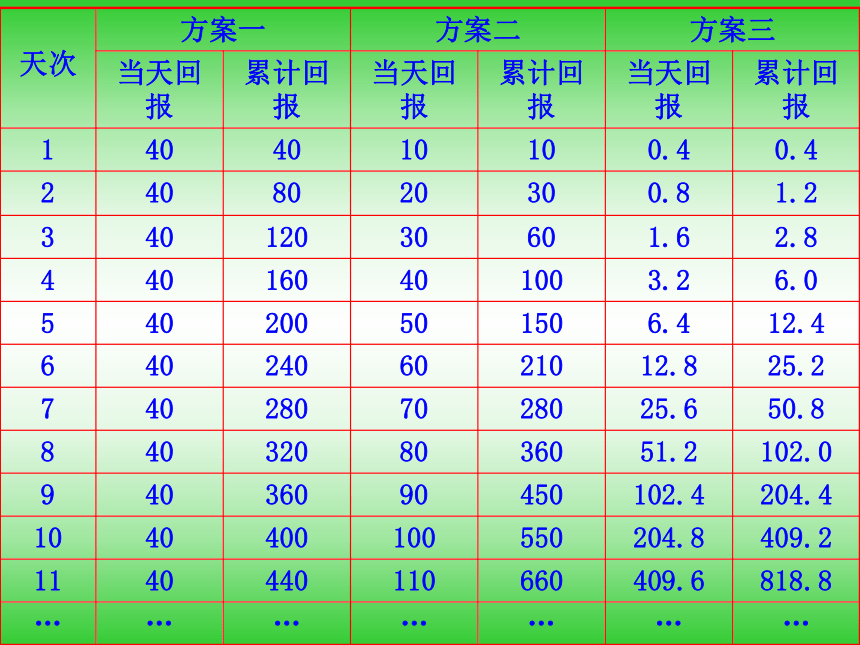
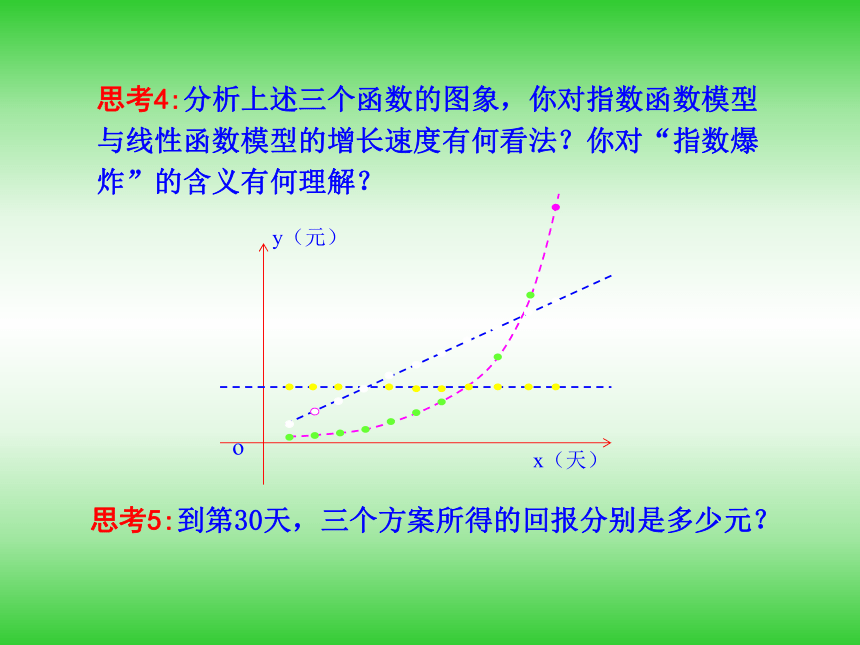
请问,你会选择哪种投资方案?思考1:设第x天所得的回报为y元,那么上述三种投资方案对应的函数模型分别是什么? 知识探究(一):无条件函数模型的选择思考2:上述三个函数分别是什么类型的函数?其单调性如何? 思考3:这三个方案前11天所得的回报如下表,分析这些数据,你如何根据投资天数选择投资方案?思考4:分析上述三个函数的图象,你对指数函数模型与线性函数模型的增长速度有何看法?你对“指数爆炸”的含义有何理解?思考5:到第30天,三个方案所得的回报分别是多少元?问题: 某公司为了实现1000万元利润的目标,准备制定
一个激励销售人员的奖励方案: 在销售利润达到10万元
时,按销售利润进行奖励,且奖金y(单位: 万元)随销
售利润x(单位: 万元)的增加而增加,但奖金总数不超
过5万元,同时奖金不超过利润的25%.现有三个奖励模型: , , 中哪个模
型能符合公司的要求?知识探究(二):有条件函数模型的选择思考1:根据问题要求,奖金数y应满足哪几个不等式? 思考2:销售人员获得奖励,其销售利润x(单位: 万元)的取值范围大致如何?思考3:确定三个奖励模型中哪个能符合公司的要求,其本质是解决一个什么数学问题? 思考4:对于模型y=0.25x,符合要求吗?为什么? 思考5:对于模型 ,当y=5时,
对应的x的值约是多少?该模型符合要求吗?思考6:对于函数 ,当x∈[10,1000]时,
y的最大值约为多少? 思考7:当x∈[10,1000]时,如何判断
是否成立? 考点一: 一次函数与指数函数理论迁移[例1] 甲、乙两城市现有人口总数为100万人,甲城市人口的年自然增长率为1.2%,乙城市每年增长人口1.3万.试解答下面的问题:
(1)写出两城市的人口总数y(万人)与年份x(年)的函数关系式;
(2)计算10年、20年、30年后两城市的人口总数(精确到0.1万人);(3)对两城市人口增长情况作出分析.
提示:(1+1.2%)10≈1.127,(1+1.2%)20≈1.269,(1+1.2%)30≈1.430.[精解详析] (1)1年后甲城市人口总数为:
y甲=100+100×1.2%=100×(1+1.2%);
2年后甲城市人口总数为:
y甲=100×(1+1.2%)+100×(1+1.2%)×1.2%
=100×(1+1.2%)2;
3年后甲城市人口总数为:y甲=100×(1+1.2%)3;
……
x年后甲城市人口总数y甲=100×(1+1.2%)x,乙城市人口总数y乙=100+1.3x.(2)10年、20年、30年后甲、乙两城市人口总数(单位:万人)如下表:(3)甲、乙两城市人口都是逐年增长,而甲城市人口增长的速度快些.从中可以体会到,不同的函数增长模型,增长变化存在很大差异.[一点通] 本例是一个有关平均增长率的问题,其基本运算方法是:如果原来产值的基础数为N,平均增长率为p,则对于时间x的总产值y可以用下面的公式,即y=N(1+p)x来表示.解决平均增长率的问题,常用到这个函数模型.1.某种细菌在培养过程中,每15 min分裂一次(由1个分
裂成2个).这种细菌由1个分裂成4 096个需经过( )
A.12 h B.4 h
C.3 h D.2 h答案:C2.某医药研究所开发一种新药,如果
成年人按规定的剂量服用,据监测,
服药后每毫升血液中的含药量y(毫
克)与时间t(小时)之间近似满足如
图所示的曲线.
(1)写出服药后y与t之间的函数关系式y=f(t);
(2)进一步测定:每毫升血液中含药量不少于0.25毫克时,药物对治疗疾病有效.求服药一次治疗疾病的有效时间.考点二: 对数函数模型[一点通] 解决此类问题首先要明确各个量所代表的实际意义,然后利用对数运算性质或换底公式求解.3.某研究小组在一项实验中获得一组关于y、t的数据,
将其整理得到如图所示的图形.下列函数中,最能近似刻画y与t之间关系的是 ( )A.y=2t B.y=2t2
C.y=t3 D.y=log2t解析:由图知该函数可能是y=log2t.
答案:D4.(2011·湖南高考)里氏震级M的计算公式为:M=lg A-
lg A0,其中A是测震仪记录的地震曲线的最大振幅,A0是相应的标准地震的振幅.假设在一次地震中,测震仪记录的最大振幅是1 000,此时标准地震的振幅为0.001,则此次地震的震级为________级,9级地震的最大振幅是5级地震最大振幅的________倍.解析:由lg 1 000-lg 0.001=6,得此次地震的震级为6级.标准地震的振幅为0.001,设9级地震最大振幅为A9,则可得lg A9-lg 0.001=9,解得A9=106.同理5级地震最大振幅A5=102,所以9级地震的最大振幅是5级的10 000倍.
答案:6 10 000[例3] (12分)函数f(x)=2x和g(x)=x3的图象如图所示.设两函数的图象交于点A(x1,y1),B(x2,y2),且x1(1)指出曲线C1,C2分别对应哪一个函数;
(2)结合函数图象,比较f(8),g(8),
f(2 012),g(2 012)的大小.考点三: 几类函数模型的比较[精解详析] (1)C1对应的函数为g(x)=x3, (2分)
C2对应的函数为f(x)=2x. (4分)
(2)∵g(1)=1,f(1)=2,g(2)=8,f(2)=4,g(9)=729,
f(9)=512,g(10)=1 000,f(10)=1 024, (6分)
∴f(1)>g(1),f(2)g(10). (8分)∴1由图象知,当x1当x>x2时,f(x)>g(x),
且g(x)在(0,+∞)上是增函数. (11分)
∴f(2 012)>g(2 012)>g(8)>f(8). (12分)[一点通] 根据图象判断增长型的指数函数、对数函数和幂函数时,通常是观察函数图象上升的快慢,即随着自变量的增大,图象最“陡”的函数是指数函数,图象趋于平缓的是对数函数.5.函数f(x)=lg x,g(x)=0.3x-1的
图象如图.
(1)指出C1,C2分别对应图中哪一个函数;
(2)比较两函数的增长差异(以两图象交点为分界点,对f(x),g(x)的大小进行比较).解:(1)C1对应的函数为g(x)=0.3x-1,
C2对应的函数为f(x)=lg x.
(2)当x∈(0,x1)时,g(x)>f(x);
当x∈(x1,x2)时,g(x)当x∈(x2,+∞)时,g(x)>f(x).6.某市有甲、乙两家乒乓球俱乐部,两家的设备和服务
都很好,但收费方式不同.甲家每张球台每小时5元;乙家按月计费,一个月中30小时以内(含30小时)每张球台90元,超过30小时的部分每张球台每小时2元.小张准备下个月从这两家中的一家租一张球台开展活动,其活动时间不少于15小时,也不超过40小时.(1)设在甲、乙两家租一张球台开展活动x小时的收费分别为f(x),g(x)(15≤x≤40,单位:元).求f(x),g(x)的表达式.
(2)试分析小张选择哪家较合算.(2)当30g(x).
当15≤x≤30时,由f(x)>g(x)得x>18;
由f(x)所以当15≤x<18时选甲家合算;当x=18时选甲家、乙家都一样;当x>18时选乙家合算.方法规律小结1.建立数学模型是解决数学问题的主要方法,数学建模一般分为识模、析模、建模、解模、验模五个步骤.
识模就是把应用问题的外部信息和自己已有的内部经验相对照,初步判断问题解决的方向;析模就是精读问题,做到“咬文嚼字”,抓住关键字词,化简转换问题,注意已知量,发现未知量,挖掘隐含量;建模是通过数学符号,把问题转化为数学模型的过程;解模时我们可以借助计算机等数学工具对所建模型求解;由于应用问题本身的繁杂性、开放性,根据自己理解所建立的模型也有局限性,最后要对模型的解检验,或取或舍,或重新修正模型,直到满意为止.有些问题还需要我们利用信息技术收集数据、绘图、计算、拟合函数. 2.三种函数模型的选取
(1)当增长速度变化很快时,常常选用指数函数模型.
(2)当要求不断增长,但又不会增长过快,也不会增长到很大时,常常选用对数函数模型.
(3)幂函数模型y=xn(n>0)则可以描述增长幅度不同的变化:n值较小(n≤1)时,增长较慢;n值较大(n>1)时,增长较快.同学们 再见!
假设你有一笔资金用于投资, 现有三种投资方案供你选择,这三种方案的回报如下:
方案一: 每天回报40元;
方案二: 第一天回报10元, 以后每天比前一天多回报10元;
方案三: 第一天回报0.4元, 以后每天的回报比前一天翻一番.
请问,你会选择哪种投资方案?思考1:设第x天所得的回报为y元,那么上述三种投资方案对应的函数模型分别是什么? 知识探究(一):无条件函数模型的选择思考2:上述三个函数分别是什么类型的函数?其单调性如何? 思考3:这三个方案前11天所得的回报如下表,分析这些数据,你如何根据投资天数选择投资方案?思考4:分析上述三个函数的图象,你对指数函数模型与线性函数模型的增长速度有何看法?你对“指数爆炸”的含义有何理解?思考5:到第30天,三个方案所得的回报分别是多少元?问题: 某公司为了实现1000万元利润的目标,准备制定
一个激励销售人员的奖励方案: 在销售利润达到10万元
时,按销售利润进行奖励,且奖金y(单位: 万元)随销
售利润x(单位: 万元)的增加而增加,但奖金总数不超
过5万元,同时奖金不超过利润的25%.现有三个奖励模型: , , 中哪个模
型能符合公司的要求?知识探究(二):有条件函数模型的选择思考1:根据问题要求,奖金数y应满足哪几个不等式? 思考2:销售人员获得奖励,其销售利润x(单位: 万元)的取值范围大致如何?思考3:确定三个奖励模型中哪个能符合公司的要求,其本质是解决一个什么数学问题? 思考4:对于模型y=0.25x,符合要求吗?为什么? 思考5:对于模型 ,当y=5时,
对应的x的值约是多少?该模型符合要求吗?思考6:对于函数 ,当x∈[10,1000]时,
y的最大值约为多少? 思考7:当x∈[10,1000]时,如何判断
是否成立? 考点一: 一次函数与指数函数理论迁移[例1] 甲、乙两城市现有人口总数为100万人,甲城市人口的年自然增长率为1.2%,乙城市每年增长人口1.3万.试解答下面的问题:
(1)写出两城市的人口总数y(万人)与年份x(年)的函数关系式;
(2)计算10年、20年、30年后两城市的人口总数(精确到0.1万人);(3)对两城市人口增长情况作出分析.
提示:(1+1.2%)10≈1.127,(1+1.2%)20≈1.269,(1+1.2%)30≈1.430.[精解详析] (1)1年后甲城市人口总数为:
y甲=100+100×1.2%=100×(1+1.2%);
2年后甲城市人口总数为:
y甲=100×(1+1.2%)+100×(1+1.2%)×1.2%
=100×(1+1.2%)2;
3年后甲城市人口总数为:y甲=100×(1+1.2%)3;
……
x年后甲城市人口总数y甲=100×(1+1.2%)x,乙城市人口总数y乙=100+1.3x.(2)10年、20年、30年后甲、乙两城市人口总数(单位:万人)如下表:(3)甲、乙两城市人口都是逐年增长,而甲城市人口增长的速度快些.从中可以体会到,不同的函数增长模型,增长变化存在很大差异.[一点通] 本例是一个有关平均增长率的问题,其基本运算方法是:如果原来产值的基础数为N,平均增长率为p,则对于时间x的总产值y可以用下面的公式,即y=N(1+p)x来表示.解决平均增长率的问题,常用到这个函数模型.1.某种细菌在培养过程中,每15 min分裂一次(由1个分
裂成2个).这种细菌由1个分裂成4 096个需经过( )
A.12 h B.4 h
C.3 h D.2 h答案:C2.某医药研究所开发一种新药,如果
成年人按规定的剂量服用,据监测,
服药后每毫升血液中的含药量y(毫
克)与时间t(小时)之间近似满足如
图所示的曲线.
(1)写出服药后y与t之间的函数关系式y=f(t);
(2)进一步测定:每毫升血液中含药量不少于0.25毫克时,药物对治疗疾病有效.求服药一次治疗疾病的有效时间.考点二: 对数函数模型[一点通] 解决此类问题首先要明确各个量所代表的实际意义,然后利用对数运算性质或换底公式求解.3.某研究小组在一项实验中获得一组关于y、t的数据,
将其整理得到如图所示的图形.下列函数中,最能近似刻画y与t之间关系的是 ( )A.y=2t B.y=2t2
C.y=t3 D.y=log2t解析:由图知该函数可能是y=log2t.
答案:D4.(2011·湖南高考)里氏震级M的计算公式为:M=lg A-
lg A0,其中A是测震仪记录的地震曲线的最大振幅,A0是相应的标准地震的振幅.假设在一次地震中,测震仪记录的最大振幅是1 000,此时标准地震的振幅为0.001,则此次地震的震级为________级,9级地震的最大振幅是5级地震最大振幅的________倍.解析:由lg 1 000-lg 0.001=6,得此次地震的震级为6级.标准地震的振幅为0.001,设9级地震最大振幅为A9,则可得lg A9-lg 0.001=9,解得A9=106.同理5级地震最大振幅A5=102,所以9级地震的最大振幅是5级的10 000倍.
答案:6 10 000[例3] (12分)函数f(x)=2x和g(x)=x3的图象如图所示.设两函数的图象交于点A(x1,y1),B(x2,y2),且x1
(2)结合函数图象,比较f(8),g(8),
f(2 012),g(2 012)的大小.考点三: 几类函数模型的比较[精解详析] (1)C1对应的函数为g(x)=x3, (2分)
C2对应的函数为f(x)=2x. (4分)
(2)∵g(1)=1,f(1)=2,g(2)=8,f(2)=4,g(9)=729,
f(9)=512,g(10)=1 000,f(10)=1 024, (6分)
∴f(1)>g(1),f(2)
且g(x)在(0,+∞)上是增函数. (11分)
∴f(2 012)>g(2 012)>g(8)>f(8). (12分)[一点通] 根据图象判断增长型的指数函数、对数函数和幂函数时,通常是观察函数图象上升的快慢,即随着自变量的增大,图象最“陡”的函数是指数函数,图象趋于平缓的是对数函数.5.函数f(x)=lg x,g(x)=0.3x-1的
图象如图.
(1)指出C1,C2分别对应图中哪一个函数;
(2)比较两函数的增长差异(以两图象交点为分界点,对f(x),g(x)的大小进行比较).解:(1)C1对应的函数为g(x)=0.3x-1,
C2对应的函数为f(x)=lg x.
(2)当x∈(0,x1)时,g(x)>f(x);
当x∈(x1,x2)时,g(x)
都很好,但收费方式不同.甲家每张球台每小时5元;乙家按月计费,一个月中30小时以内(含30小时)每张球台90元,超过30小时的部分每张球台每小时2元.小张准备下个月从这两家中的一家租一张球台开展活动,其活动时间不少于15小时,也不超过40小时.(1)设在甲、乙两家租一张球台开展活动x小时的收费分别为f(x),g(x)(15≤x≤40,单位:元).求f(x),g(x)的表达式.
(2)试分析小张选择哪家较合算.(2)当30
当15≤x≤30时,由f(x)>g(x)得x>18;
由f(x)
识模就是把应用问题的外部信息和自己已有的内部经验相对照,初步判断问题解决的方向;析模就是精读问题,做到“咬文嚼字”,抓住关键字词,化简转换问题,注意已知量,发现未知量,挖掘隐含量;建模是通过数学符号,把问题转化为数学模型的过程;解模时我们可以借助计算机等数学工具对所建模型求解;由于应用问题本身的繁杂性、开放性,根据自己理解所建立的模型也有局限性,最后要对模型的解检验,或取或舍,或重新修正模型,直到满意为止.有些问题还需要我们利用信息技术收集数据、绘图、计算、拟合函数. 2.三种函数模型的选取
(1)当增长速度变化很快时,常常选用指数函数模型.
(2)当要求不断增长,但又不会增长过快,也不会增长到很大时,常常选用对数函数模型.
(3)幂函数模型y=xn(n>0)则可以描述增长幅度不同的变化:n值较小(n≤1)时,增长较慢;n值较大(n>1)时,增长较快.同学们 再见!
