6.2 排列与组合 学案(Word版含解析)
文档属性
| 名称 | 6.2 排列与组合 学案(Word版含解析) | 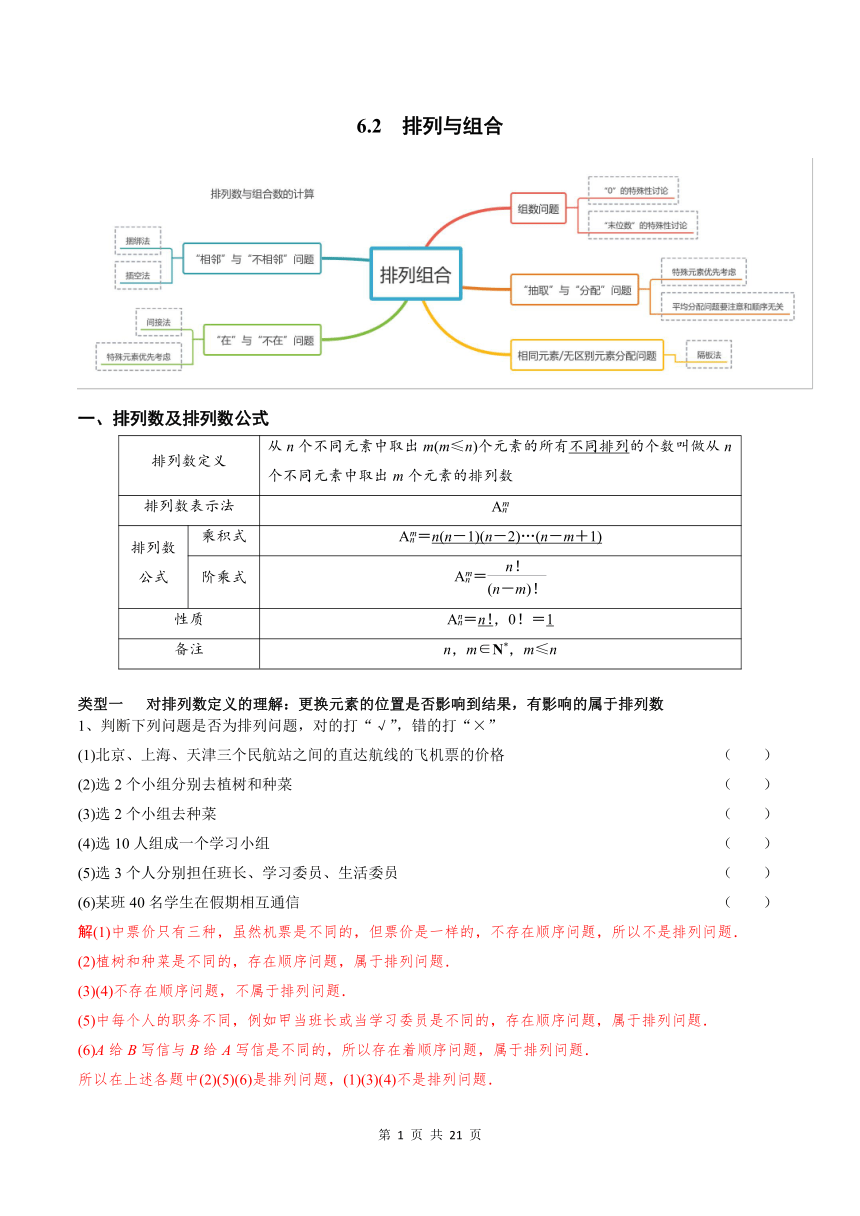 | |
| 格式 | docx | ||
| 文件大小 | 347.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-17 06:51:39 | ||
图片预览





文档简介
6.2 排列与组合
一、排列数及排列数公式
排列数定义 从n个不同元素中取出m(m≤n)个元素的所有不同排列的个数叫做从n个不同元素中取出m个元素的排列数
排列数表示法 A
排列数公式 乘积式 A=n(n-1)(n-2)…(n-m+1)
阶乘式 A=
性质 A=n!,0!=1
备注 n,m∈N*,m≤n
类型一 对排列数定义的理解:更换元素的位置是否影响到结果,有影响的属于排列数
1、判断下列问题是否为排列问题,对的打“√”,错的打“×”
(1)北京、上海、天津三个民航站之间的直达航线的飞机票的价格 ( )
(2)选2个小组分别去植树和种菜 ( )
(3)选2个小组去种菜 ( )
(4)选10人组成一个学习小组 ( )
(5)选3个人分别担任班长、学习委员、生活委员 ( )
(6)某班40名学生在假期相互通信 ( )
解(1)中票价只有三种,虽然机票是不同的,但票价是一样的,不存在顺序问题,所以不是排列问题.
(2)植树和种菜是不同的,存在顺序问题,属于排列问题.
(3)(4)不存在顺序问题,不属于排列问题.
(5)中每个人的职务不同,例如甲当班长或当学习委员是不同的,存在顺序问题,属于排列问题.
(6)A给B写信与B给A写信是不同的,所以存在着顺序问题,属于排列问题.
所以在上述各题中(2)(5)(6)是排列问题,(1)(3)(4)不是排列问题.
类型二 排列数公式及应用:注意选择乘积式还是阶乘式
2、(x-3)(x-4)(x-5)…(x-12)(x-13),x∈N*,x>13可表示为( )
A.A B.A C.A D.A
答案 B
解析 从(x-3),(x-4),…到(x-13)共(x-3)-(x-13)+1=11(个)数,所以根据排列数公式知(x-3)(x-4)(x-5)…(x-12)(x-13)=A.
3、用排列数表示(55-n)(56-n)…(69-n)= (n∈N*且,n<55)
解 因为55-n,56-n,…,69-n中的最大数为69-n,且共有69-n-(55-n)+1=15(个)元素,
所以(55-n)(56-n)…(69-n)=A.
4、计算=
解 ===1.
5、求证:A-A=mA.
解 因为A-A=-=·=·
=m·=mA,所以A-A=mA.
6、解方程A=140A.
解 根据题意,原方程等价于
即
整理得4x2-35x+69=0(x≥3,x∈N*),
解得x=3.
排列的综合应用
类型一 无限制条件的排列问题
注意事项:典型的排列问题,用排列数计算其排列方法数;若不是排列问题,需用计数原理求其方法种数.排列的概念很清楚,要从“n个不同的元素中取出m个元素”.即在排列问题中元素不能重复选取,而在用分步乘法计数原理解决的问题中,元素可以重复选取.
6、有7本不同的书,从中选3本送给3名同学,每人各1本,共有 种不同的送法。
解 从7本不同的书中选3本送给3名同学,相当于从7个元素中任取3个元素的一个排列,所以共有A=7×6×5=210(种)不同的送法.
7、有7种不同的书,要买3本送给3名同学,每人各1本,共有 种不同的送法。
解 从7种不同的书中买3本书,这3本书并不要求都不相同,根据分步乘法计数原理,共有7×7×7=343(种)不同的送法.
8、有5个不同的科研小课题,从中选3个由高二(6)班的3个学习兴趣小组进行研究,每组一个课题,
共有 种不同的安排方法。
解 从5个不同的课题中选出3个,由兴趣小组进行研究,对应于从5个不同元素中取出3个元素的一个排列,因此不同的安排方法有A=5×4×3=60(种).
9、有5个不同的科研小课题,高二(6)班的3个学习兴趣小组报名参加,每组限报一个课题,共有 种不同的报名方法。
解 由题意知3个兴趣小组可能报同一科研课题,因此元素可以重复,不是排列问题.
由于每个兴趣小组都有5种不同的选择,且3个小组都选择完才算完成这件事,所以由分步乘法计数原理得共有5×5×5=125(种)报名方法.
类型二 排队问题
解题原则:“处理元素“相邻”“不相邻”问题应遵循“先整体,后局部”的原则.
解题方法:①元素相邻问题,一般用“捆绑法”,先把相邻的若干个元素“捆绑”为一个大元素与其余元素全排列,然后再松绑,将这若干个元素内部全排列.
②元素不相邻问题,一般用“插空法”,先将不相邻元素以外的“普通”元素全排列,然后在“普通”元素之间及两端插入不相邻元素.
10、5位母亲带领5名儿童站成一排照相,儿童不相邻的站法有________种.(可用排列数表示)
答案 86400
解析 第1步,先排5位母亲的位置,有A种排法;
第2步,把5名儿童插入5位母亲所形成的6个空位中,如下所示:
母亲____母亲____母亲____母亲____母亲____,共有A种排法.
由分步乘法计数原理可知,符合条件的站法共有A·A=86 400(种).
11、两家夫妇各带一个小孩一起去公园游玩,购票后排队依次入园.为安全起见,首尾一定要排两位爸爸,另外,两个小孩一定要排在一起,则这6人的入园顺序排法种数为________.
答案 24
解析 分3步进行分析,
①先安排两位爸爸,必须一首一尾,有A=2(种)排法,
②两个小孩一定要排在一起,将其看成一个元素,考虑其顺序有A=2(种)排法,
③将两个小孩看作一个元素与两位妈妈进行全排列,有A=6(种)排法.则共有2×2×6=24(种)排法.
12、3名男生、4名女生按照不同的要求排队,求不同的排队方法的种数.
(1)全体站成一排,男、女各站在一起;
(2)全体站成一排,男生必须站在一起;
(3)全体站成一排,男生不能站在一起;
(4)全体站成一排,男、女各不相邻.
解 (1)男生必须站在一起是男生的全排列,有A种排法;
女生必须站在一起是女生的全排列,有A种排法;
全体男生、女生各视为一个元素,有A种排法.
由分步乘法计数原理知,共有A·A·A=288(种)排队方法.
(2)三个男生全排列有A种方法,把所有男生视为一个元素,与4名女生组成5个元素全排列,有A种排法.故有A·A=720(种)排队方法.
(3)先安排女生,共有A种排法;男生在4个女生隔成的五个空中安排,共有A种排法,故共有A·A=1 440(种)排法.
(4)排好男生后让女生插空,共有A·A=144(种)排法.
13、某次文艺晚会上共演出8个节目,其中2个唱歌、3个舞蹈、3个曲艺节目,求分别满足下列条件的节目编排方法有多少种?
(1)一个唱歌节目开头,另一个放在最后压台;
(2)2个唱歌节目互不相邻;
(3)2个唱歌节目相邻且3个舞蹈节目不相邻.
解 (1)先排唱歌节目有A种排法,再排其他节目有A种排法,所以共有A·A=1 440(种)排法.
(2)先排3个舞蹈节目和3个曲艺节目有A种排法,再从其中7个空(包括两端)中选2个排唱歌节目,有A种插入方法,所以共有A·A=30 240(种)排法.
(3)把2个相邻的唱歌节目看作一个元素,与3个曲艺节目排列共A种排法,再将3个舞蹈节目插入,共有A种插入方法,最后将2个唱歌节目互换位置,有A种排法,故所求排法共有A·A·A=2 880(种)排法.
解题原则:解“在”与“不在”的有限制条件的排列问题时,可以从元素入手也可以从位置入手,原则是谁特殊谁优先.
解题方法:从元素入手时,先给特殊元素安排位置,再把其他元素安排在其他位置上,从位置入手时,先安排特殊位置,再安排其他位置.
易错提醒:解题时,或从元素考虑,或从位置考虑,都要贯彻到底.不能一会考虑元素,一会考虑位置,造成分类、分步混乱,导致解题错误.
14、6位选手依次演讲,其中选手甲不排在第一个也不排在最后一个演讲,则不同的演讲次序共有( )
A.240种 B.360种 C.480种 D.720种
答案 C
解析 第一步:排甲,共有A种不同的排法;第二步:排其他人,共有A种不同的排法,因此不同的演讲次序共有AA=480(种).
15、某单位安排7位员工在10月1日至7日值班,每天安排1人,每人值班1天.若7位员工中的甲、乙被安排在相邻两天值班,丙不在10月1日值班,丁不在10月7日值班,则不同的安排方案共有( )
A.504种 B.960种 C.1108种 D.1008种
答案 D
解析 由题意知,满足甲、乙两人被安排在相邻两天值班的方案共有AA=1 440(种),其中满足甲、乙两人被安排在相邻两天值班且丙在10月1日值班的方案共有AA=240(种),满足甲、乙两人被安排在相邻两天值班且丁在10月7日值班的方案共有AA=240(种),满足甲、乙两人安排在相邻两天值班且丙在10月1日值班、丁在10月7日值班的方案共有AA=48(种).因此满足题意的方案共有1 440-2×240+48=1008(种).
16、某一天的课程表要排入政治、语文、数学、物理、体育、美术共六节课,如果第一节不排体育,最后一节不排数学,那么共有 种不同的排课程表的方法。
解 6门课总的排法是A,其中不符合要求的可分为体育排在第一节,有A种排法;数学排在最后一节,有A种排法,但这两种方法,都包括体育排在第一节,数学排在最后一节,这种情况有A种排法.因此符合条件的排法有A-2A+A=504(种).
17、六人按下列要求站一横排,分别有多少种不同的站法?
(1)甲不能在两端;
(2)甲、乙必须在两端;
(3)甲不在最左端,乙不在最右端.
解 (1)先考虑甲有A种方案,再考虑其余5人全排列,故N=A·A=480(种);
(2)先安排甲、乙有A种方案,再安排其余4人全排列,故N=A·A=48(种);
(3)方法一 甲在最左端的站法有A种,乙在最右端的站法有A种,且甲在最左端而乙在最右端的站法有A种,共有A-2A+A=504(种)站法.
方法二 以元素甲分类可分为两类:a.甲站最右端有A种,b.甲在中间4个位置之一,而乙不在最右端有A·A·A种,故共有A+A·A·A=504(种)站法.
在有些排列问题中,某些元素有前后顺序是确定的(不一定相邻),解决这类问题的基本方法有两种:
①整体法:即若有m+n个元素排成一列,其中m个元素之间的先后顺序确定不变,先将这m+n个元素排成一列,有A种不同的排法;然后任取一个排列,固定其他n个元素的位置不动,把这m个元素交换顺序,有A种排法,其中只有一个排列是我们需要的,因此共有种满足条件的不同排法.
②插空法:即m个元素之间的先后顺序确定不变,因此先排这m个元素,只有一种排法,然后把剩下的n个元素分类或分步插入由以上m个元素形成的空隙中.
18、将A,B,C,D,E这5个字母排成一列,要求A,B,C在排列中的顺序为“A,B,C”或“C,B,A”(可以不相邻).则有 种不同的排列方法。
解 5个不同元素中部分元素A,B,C的排列顺序已定,这种问题有以下两种常用的解法.
方法一 (整体法)5个元素无约束条件的全排列有A种,由于字母A,B,C的排列顺序为“A,B,C”或“C,B,A”,因此,在上述的全排列中恰好符合“A,B,C”或“C,B,A”排列方式的排列有×2=40(种).
方法二 (插空法)若字母A,B,C的排列顺序为“A,B,C”,将字母D,E插入,这时形成的4个空中,分两类:
第一类,若字母D,E相邻,则有A·A种排法;
第二类,若字母D,E不相邻,则有A种排法.
所以有A·A+A=20(种)不同的排列方法.
同理,若字母A,B,C的排列顺序为“C,B,A”,也有20种不同的排列方法.
因此,满足条件的排列有20+20=40(种).
19、用1,2,3,4,5,6,7组成没有重复数字的七位数,若1,3,5,7的顺序一定,则有________个七位数符合条件.
答案 210
解析 若1,3,5,7的顺序不定,有A=24(种)排法,故1,3,5,7的顺序一定的排法数只占总排法数的.
故有A=210(个)七位数符合条件.
类型三 数字排列问题
数字排列的常见特殊性:(1)首位不能为0;(2)有无重复数字;(3)奇偶数;(4)某数的倍数;(5)大于(或小于)某数.
20、用0,1,2,3,4,5这六个数字可以组成多少个符合下列条件的无重复的数字?
(1)六位奇数;
(2)个位数字不是5的六位数;
(3)不大于4310的四位偶数.
解 (1)第一步,排个位,有A种排法;
第二步,排十万位,有A种排法;
第三步,排其他位,有A种排法.
故共有AAA=288(个)六位奇数.
(2)方法一 (直接法):
十万位数字的排法因个位上排0与不排0而有所不同,因此需分两类.
第一类,当个位排0时,有A个;
第二类,当个位不排0时,有AAA个.
故符合题意的六位数共有A+AAA=504(个).
方法二 (排除法):
0在十万位和5在个位的排列都不对应符合题意的六位数,这两类排列中都含有0在十万位和5在个位的情况.
故符合题意的六位数共有A-2A+A=504(个).
(3)分三种情况,具体如下:
①当千位上排1,3时,有AAA个.
②当千位上排2时,有AA个.
③当千位上排4时,形如4 0×2,4 2×0的各有A个;
形如4 1××的有AA个;
形如4 3××的只有4 310和4 302这两个数.
故共有AAA+AA+2A+AA+2=110(个).
21、用0,1,2,3,4,5这六个数字可以组成多少个无重复数字的
(1)能被5整除的五位数;
(2)能被3整除的五位数;
(3)若所有的六位数按从小到大的顺序组成一个数列{an},则240135是第几项.
解 (1)个位上的数字必须是0或5.个位上是0,有A个;个位上是5,若不含0,则有A个;若含0,但0不作首位,则0的位置有A种排法,其余各位有A种排法,故共有A+A+AA=216(个)能被5整除的五位数.
(2)能被3整除的条件是各位数字之和能被3整除,则5个数可能有{1,2,3,4,5}和{0,1,2,4,5}两种情况,能够组成的五位数分别有A个和AA个.
故能被3整除的五位数有A+AA=216(个).
(3)由于是六位数,首位数字不能为0,首位数字为1有A个数,首位数字为2,万位上为0,1,3中的一个,有3A个数,
∴240 135的项数是A+3A+1=193,
即240135是数列的第193项.
三、组合数与组合数公式
组合数定义及表示 从n个不同元素中取出m(m≤n)个元素的所有不同组合的个数,叫做从n个不同元素中取出m个元素的组合数,用符号C表示.
组合数公式 乘积形式 C=
阶乘形式 C=
性质 C=C C=C+C
备注 规定C=1
类型一 组合概念的理解
排列与组合的区别:区分排列与组合的办法是首先弄清楚事件是什么,区分的标志是有无顺序,而区分有无顺序的方法是:把问题的一个选择结果写出来,然后交换这个结果中任意两个元素的位置,看是否产生新的变化,若有新变化,即说明有顺序,是排列问题;若无新变化,即说明无顺序,是组合问题.
22、判断下列问题是排列还是组合问题,排列打“√”,组合打“×”
(1)a,b,c,d四支足球队之间进行单循环比赛,共需比赛多少场 。 ( )
(2)a,b,c,d四支足球队争夺冠、亚军,有多少种不同的结果 。 ( )
(3)从全班40人中选出3人分别担任班长、副班长、学习委员三个职务,有多少种不同的选法 ( )
(4)从全班40人中选出3人参加某项活动,有多少种不同的选法 ( )
解 (1)单循环比赛要求两支球队之间只打一场比赛,没有顺序,是组合问题.
(2)冠、亚军是有顺序的,是排列问题.
(3)3人分别担任三个不同职务,有顺序,是排列问题.
(4)3人参加某项相同活动,没有顺序,是组合问题.
类型二 组合数公式及性质的应用
注意运用一下技巧:
(1)涉及具体数字的可以直接用公式C==计算.
(2)涉及字母的可以用阶乘式C=计算.
(3)计算时应注意利用组合数的两个性质:
①C=C;②C=C+C.
23、计算C+C+C+…+C的值为( )
A.C B.C
C.C-1 D.C-1
解析 C+C+C+…+C=C+C+C+C+…+C-C=C+C+…+C-1=…
=C+C-1=C-1.
24、计算C+C=________.
解析 C+C=C+C=+200=5150.
25、计算C-C·A=
解 原式=C-A=-7×6×5=210-210=0.
26、求证:C=C.
证明 因为右边=C=·==C,
左边=C,所以左边=右边,所以原式成立.
27、已知-=,求C+C
解 (1)∵-=,
∴-=,
即-
=.
∴1-=,
即m2-23m+42=0,解得m=2或21.
∵0≤m≤5,∴m=2,
∴C+C=C+C=C=84.
28、解不等式C>C.
(2)由C>C,得
即解得
又n∈N*,∴该不等式的解集为{6,7,8,9}.
29、解方程3C=5A.
解 原式可变形为3C=5A,
即
=5(x-4)(x-5),
所以(x-3)(x-6)=5×4×2=8×5.
所以x=11或x=-2(舍去).
经检验符合题意,所以方程的解为x=11.
四、组合的综合应用
类型一 简单的组合问题(无限制的组合问题)
①解简单的组合应用题时,首先要判断它是不是组合问题,组合问题与排列问题的根本区别在于排列问题与取出元素之间的顺序有关,而组合问题与取出元素的顺序无关.
②要注意两个基本原理的运用,即分类与分步的灵活运用.
在分类和分步时,一定注意有无重复或遗漏.
30、有10名教师,其中6名男教师,4名女教师.
(1)现要从中选2名去参加会议,有________种不同的选法;
(2)选出2名男教师或2名女教师参加会议,有________种不同的选法;
(3)现要从中选出男、女教师各2名去参加会议,有________种不同的选法.
答案 (1)45 (2)21 (3)90
解析 (1)从10名教师中选2名去参加会议的选法种数,就是从10个不同元素中取出2个元素的组合数,即C==45(种).
(2)可把问题分两类情况:
第1类,选出的2名是男教师有C种方法;
第2类,选出的2名是女教师有C种方法.
根据分类加法计算原理,共有C+C=15+6=21(种)不同选法.
(3)从6名男教师中选2名的选法有C种,从4名女教师中选2名的选法有C种,根据分步乘法计数原理,共有不同的选法C×C=×=90(种).
31、一个口袋内装有大小相同的7个白球和1个黑球.
(1)从口袋内取出的3个小球,共有 种取法?
(2)从口袋内取出3个球,使其中含有1个黑球,有 种取法?
(3)从口袋内取出3个球,使其中不含黑球,有 种取法?
解 (1)从口袋内的8个球中取出3个球,
取法种数是C==56.
(2)从口袋内取出3个球有1个是黑球,于是还要从7个白球中再取出2个,取法种数是C==21.
(3)由于所取出的3个球中不含黑球,也就是要从7个白球中取出3个球,取法种数是C==35.
类型二 有限制条件的组合问题
常考的两类问题:
①“含”与“不含”问题,其解法常用直接分步法,即“含”的先取出,“不含”的可把所指元素去掉再取,分步计数;
②“至多”“至少”问题,其解法常有两种解决思路:一是直接分类法,但要注意分类要不重不漏;二是间接法,注意找准对立面,确保不重不漏.
32、某食堂每天中午准备4种不同的荤菜,7种不同的蔬菜,用餐者可以按下述方法之一搭配午餐:(1)任选两种荤菜、两种蔬菜和白米饭;(2)任选一种荤菜、两种蔬菜和蛋炒饭.则每天不同午餐的搭配方法共有( )
A.210种 B.420种 C.56种 D.22种
答案 A
解析 由分类加法计数原理知,两类配餐的搭配方法之和即为所求,所以每天不同午餐的搭配方法共有CC+CC=210(种).
33、某乒乓球队有9名队员,其中2名是种子选手,现在挑选5名选手参加比赛,种子选手必须在内,那么不同选法共有( )
A.26种 B.84种 C.35种 D.21种
答案 C
解析 从7名队员中选出3人有C==35(种)选法.
34、身高各不相同的7名同学排成一排照相,要求正中间的同学最高,左右两边分别顺次一个比一个低,这样的排法种数是( )
A.5 040 B.36 C.18 D.20
答案 D
解析 最高的同学站中间,从余下6人中选3人在一侧只有一种站法,另3人在另一侧也只有一种站法,所以排法有C=20(种).
35、课外活动小组共13人,其中男生8人,女生5人,并且男、女生各有一名队长,现从中选5人主持某项活动,依下列条件各有多少种选法?
(1)至少有一名队长当选;
(2)至多有两名女生当选;
(3)既要有队长,又要有女生当选.
解 (1)C-C=825(种)
(2)至多有2名女生当选含有三类:
有2名女生;只有1名女生;没有女生,
所以共有CC+CC+C=966(种)选法.
(3)分两类:
第一类女队长当选,有C=495(种)选法,
第二类女队长没当选,有CC+CC+CC+C=295(种)选法,
所以共有495+295=790(种)选法.
类型三 分组、分配问题
易错点:遇到平均分成m组的情况,需要除掉
36、江西省旅游产业发展大会于2020年6月11日~13日在赣州举行,某旅游公司为推出新的旅游项目,特派出五名工作人员前往赣州三个景点进行团队游的可行性调研.若每名工作人员只去一个景点且每个景点至少有一名工作人员前往,则不同的人员分配方案种数为( )
A.60 B.90 C.150 D.240
【答案】C
【解析】根据题意,分2步进行分析:
①将五名工作人员分成3组,
若分为3、1、1的三组,有种分法,
若分为2、2、1的三组,种分法,
则有种分组分法;
②将分好的三组全排列,对应三个景点,有种情况,
则有种分配方法;
故选:.
37、疫情期间,上海某医院安排5名专家到3个不同的区级医院支援,每名专家只去一个区级医院,每个区级医院至少安排一名专家,则不同的安排方法共有( )
A.60种 B.90种 C.150种 D.240种
【答案】C
【解析】5名专家到3个不同的区级医院,分为1,2,2和1,1,3两种情况;
分为1,2,2时安排有;分为1,1,3时安排有
所以一共有
38、据《孙子算经》中记载,中国古代诸侯的等级从低到高分为:男、子、伯、侯、公,共五级,若给获得巨大贡献的7人进行封爵,要求每个等级至少有一人,至多有两人,则伯爵恰有两人的概率为( )
A. B. C. D.
【答案】B
【解析】人进行封爵,每个等级至少一人,至多两人,则共有种分法;
其中伯爵恰有两人的分法有种分法,
伯爵恰有两人的概率
39、2020年是我国脱贫攻坚决战决胜之年,某县农业局为支持该县的扶贫工作,决定派出8名农技人员(5男3女),并分成两组,分配到2个贫困村进行扶贫工作,若每组至少3人,且每组都有男农技人员,则不同的分配方案共有______种(用数字填写答案).
【答案】180
【解析】分配的方案有两类,
第一类:一组3人,另一组5人,有种;
第二类:两组均为4人,有种,
所以共有种不同的分配方案.
40、6本不同的书,分为3组,在下列条件下各有多少种不同的分配方法?
(1)每组2本(平均分组);
(2)一组1本,一组2本,一组3本(不平均分组);
(3)一组4本,另外两组各1本(局部平均分组).
解 (1)每组2本,均分为3组的方法数为==15.
(2)一组1本,一组2本,一组3本的分组种数为CCC=20×3=60.
(3)一组4本,另外两组各1本的分组种数为==15.
41、6本不同的书,分给甲、乙、丙3人,在下列条件下各有多少种不同的分配方法?
(1)甲2本,乙2本,丙2本;
(2)甲1本,乙2本,丙3本;
(3)甲4本,乙、丙每人1本;
(4)每人2本;
(5)一人1本,一人2本,一人3本;
(6)一人4本,其余两人每人1本.
解 (1)(2)(3)中,由于每人分的本数固定,属于定向分配问题,由分步乘法计数原理得:
(1)共有CCC=90(种)不同的分配方法;
(2)共有CCC=60(种)不同的分配方法;
(3)共有CCC=30(种)不同的分配方法.
(4)(5)(6)属于不定向分配问题,是该类题中比较困难的问题.分配给3人,同一本书给不同的人是不同的分法,属于排列问题.实际上可看作两个步骤:先分为3组,再把这3组分给甲、乙、丙3人的全排列数A即可.因此,(4)共有CCC÷A×A=90(种)不同的分配方法;
(5)共有CCC×A=360(种)不同的分配方法;
(6)共有CCC÷A×A=90(种)不同的分配方法.
相同元素分配问题的处理策略
(1)隔板法:如果将放有小球的盒子紧挨着成一行放置,便可看作在排成一行的小球的空隙中插入了若干隔板,相邻两块隔板形成一个“盒”.每一种插入隔板的方法对应着小球放入盒子的一种方法,此法称之为隔板法.隔板法专门解决相同元素的分配问题.
(2)将n个相同的元素分给m个不同的对象(n≥m),有C种方法.可描述为n-1个空中插入m-1块板.
42、某同学有同样的画册2本,同样的集邮册3本,从中取出4本赠送给4位朋友,每位朋友1本,则不同的赠送方法共有( )
A.4种 B.10种
C.18种 D.20种
答案 B
解析 由于只剩一本书,且这些画册、集邮册分别相同,可以从剩余的书的类别进行分析.又由于排列、组合针对的是不同的元素,应从4位朋友中进行选取.
第一类:当剩余的一本是画册时,相当于把3本相同的集邮册和1本画册分给4位朋友,只有1位朋友得到画册.即把4位朋友分成人数为1,3的两队,有1个元素的那队分给画册,另一队分给集邮册,有C种分法.
第二类:当剩余的一本是集邮册时,相当于把2本相同的画册和2本相同的集邮册分给4位朋友,有2位朋友得到画册,即把4位朋友分成人数为2,2的两队,一队分给画册,另一队分给集邮册,有C种分法.
因此,满足题意的赠送方法共有C+C=4+6=10(种).
43、假如北京大学给中山市某三所重点中学7个自主招生的推荐名额,则每所中学至少分到一个名额的方法数为( )
A.30 B.21 C.10 D.15
考点 排列组合综合问题
题点 分组分配问题
答案 D
解析 用“隔板法”.在7个名额中间的6个空位上选2个位置加2个隔板,有C=15(种)分配方法.
44、将6个相同的小球放入4个编号为1,2,3,4的盒子,求下列方法的种数.
(1)每个盒子都不空;
(2)恰有一个空盒子;
(3)恰有两个空盒子.
解 (1)先把6个相同的小球排成一行,在首尾两球外侧放置一块隔板,然后在小球之间5个空隙中任选3个空隙各插一块隔板,有C=10(种).
(2)恰有一个空盒子,插板分两步进行.先在首尾两球外侧放置一块隔板,并在5个空隙中任选2个空隙各插一块隔板,如|0|000|00|,有C种插法,然后将剩下的一块隔板与前面任意一块并放形成空盒,如|0|000||00|,有C种插法,故共有C·C=40(种).
(3)恰有两个空盒子,插板分两步进行.
先在首尾两球外侧放置一块隔板,并在5个空隙中任选1个空隙各插一块隔板,有C种插法,如|00|0000|,然后将剩下的两块隔板插入形成空盒.
①这两块板与前面三块板形成不相邻的两个盒子,
如||00||0000|,有C种插法.
②将两块板与前面三块板之一并放,如|00|||0000|,有C种插法.
故共有C·(C+C)=30(种).
课后巩固练习
1、某电视台一节目收视率很高,现要连续插播4个广告,其中2个不同的商业广告和2个不同的公益宣传广告,要求最后播放的必须是商业广告,且2个商业广告不能连续播放,则不同的播放方式有( )
A.8种 B.16种 C.18种 D.24种
答案 A
解析 可分三步:第一步,排最后一个商业广告,有A种;第二步,在前两个位置选一个排第二个商业广告,有A种;第三步,余下的两个位置排公益宣传广告,有A种.根据分步乘法计数原理,不同的播放方式共有A·A·A=8(种),故选A.
2、由1,2,3,4,5组成没有重复数字的四位数,按从小到大的顺序排成一个数列{an},则a72等于( )
A.1543 B.2543 C.3542 D.4532
答案 C
解析 首位是1的四位数有A=24(个),
首位是2的四位数有A=24(个),首位是3的四位数有A=24(个),
由分类加法计数原理得,
首位小于4的所有四位数共3×24=72(个).由此得a72=3 542.
3、若从1,2,3,…,9这9个整数中同时取3个不同的数,使其和为奇数,则不同的取法共有( )
A.30种 B.33种 C.37种 D.40种
答案 D
解析 从1,2,3,…,9这9个数中取出3个不同的数,使其和为奇数的情况包括:(1)取出的3个数都是奇数,取法有C=10(种);(2)取出的3个数中有2个偶数、1个奇数,取法有CC=30(种),根据分类加法计数原理,满足题意的取法共有10+30=40(种).
4、某班级要从4名男生、2名女生中选派4人参加某次社区服务,如果要求至少有1名女生,那么不同的选派方案种数为( )
A.24种 B.14种 C.28种 D.48种
答案 B
解析 方法一 分两类完成:
第1类,选派1名女生、3名男生,有C·C种选派方案;
第2类,选派2名女生、2名男生,有C·C种选派方案.
故共有C·C+C·C=14(种)不同的选派方案.
方法二 6人中选派4人的组合数为C,其中都选男生的组合数为C,所以至少有1名女生的选派方案有C-C=14(种).
5、由数字0,1,2,3,4,5组成没有重复数字的六位数,其中个位数字小于十位数字的共有( )
A.210个 B.300个 C.464个 D.600个
答案 B
解析 由于组成没有重复数字的六位数,个位小于十位的与个位大于十位的一样多,故有=300(个).
6、从乒乓球运动员男5名、女6名中组织一场混合双打比赛,不同的组合方法有( )
A.CC种 B.CA种
C.CACA种 D.AA种
答案 B
解析 先从5名男选手中任意选取2名,有C种选法,再从6名女选手中任意选择两名与选出的男选手打比赛,有CA,即A种.所以共有CA种.
7、将标号为A,B,C,D,E,F的6张卡片放入3个不同的信封中,若每个信封放2张卡片,其中标号为A,B的卡片放入同1个信封,则不同的放法共有( )
A.12种 B.18种 C.36种 D.54种
答案 B
解析 由题意知,不同的放法共有CC=3×=18(种).
8、某地招募了20名志愿者,他们编号分别为1号,2号,…,19号,20号,如果要从中任意选取4人再按编号大小分成两组去做一些预备服务工作,其中两个编号较小的人在一组,两个编号较大的人在另一组,那么确保5号与14号入选并被分配到同一组的选取种数是( )
A.16 B.21 C.24 D.90
答案 B
解析 分2类:
第1类,5号与14号为编号较大的一组,则另一组编号较小的有C=6(种)选取方法.
第2类,5号与14号为编号较小的一组,则编号较大的一组有C=15(种)选取方法.
由分类加法计数原理得,共有C+C=6+15=21(种)选取方法.
9、.北京《财富》全球论坛期间,某高校有14名志愿者参加接待工作,若每天早、中、晚三班,每班4人,每人每天最多值一班,则开幕式当天不同的排班种数为( )
A.CCC B.CAA
C. D.CCCA
答案 A
解析 首先从14人中选出12人共C种,然后将12人平均分为3组共种,然后这两步相乘,得.将三组分配下去共C·C·C种.故选A.
10、在制作飞机的某一零件时,要先后实施6个工序,其中工序A只能出现在第一步或最后一步,工序B和C在实施时必须相邻,则实施顺序的编排方法共有( )
A.34种 B.48种 C.96种 D.144种
答案 C
解析 由题意可知,先排工序A,有2种编排方法;再将工序B和C视为一个整体(有2种顺序)与其他3个工序全排列共有2A种编排方法.故实施顺序的编排方法共有2×2A=96(种).故选C.
11、从6名短跑运动员中选出4人参加4×100 m接力赛,甲不能跑第一棒和第四棒,问共有________种参赛方案.
答案 240
解析 方法一 从人(元素)的角度考虑,优先考虑甲,分以下两类:
第1类,甲不参赛,有A种参赛方案;
第2类,甲参赛,可优先将甲安排在第二棒或第三棒,有2种方法,然后安排其他3棒,有A种方法,此时有2A种参赛方案.
由分类加法计数原理可知,甲不能跑第一棒和第四棒的参赛方案共有A+2A=240(种).
方法二 从位置(元素)的角度考虑,优先考虑第一棒和第四棒,则这两棒可以从除甲之外的5人中选2人,有A种方法;其余两棒从剩余4人中选,有A种方法.
由分步乘法计数原理可知,甲不能跑第一棒和第四棒的参赛方案共有AA=240(种).
方法三 (排除法):不考虑甲的约束,6个人占4个位置,有A种安排方法,剔除甲跑第一棒和第四棒的参赛方案有2A种,所以甲不能跑第一棒和第四棒的参赛方案共有A-2A=240(种).
12、六个停车位置,有3辆汽车需要停放,若要使三个空位连在一起,则停放的方法数为________.
答案 24
解析 把3个空位看作一个元素,与3辆汽车共有4个元素全排列,故停放的方法有A=4×3×2×1=24(种).
13、在2017年的上海高考改革方案中,要求每位考生必须在物理、化学、生物、政治、历史、地理6门学科中选择3门学科参加等级考试.小明同学决定在生物、政治、历史三门中至多选择一门,那么小明同学的选择方案有________种.
答案 10
解析 ①在生物、政治、历史三门中选择1门,则在物理、化学、地理中选2门,有CC=9(种)选法;
②在生物、政治、历史三门中选择0门,则物理、化学、地理全选,有C=1(种)选法.
共有选法9+1=10(种).
14、如图所示的几何体是由一个正三棱锥P-ABC与正三棱柱ABC-A1B1C1组合而成,现用3种不同颜色对这个几何体的表面涂色(底面A1B1C1不涂色),要求相邻的面均不同色,则不同的涂色方案共有______种.
答案 12
解析 先涂三棱锥P-ABC的三个侧面,然后涂三棱柱的三个侧面,共有C×C×C×C=3×2×1×2=12(种)不同的涂法.
15、在8张奖券中有一、二、三等奖各1张,其余5张无奖.将这8张奖券分配给4个人,每人2张,不同的获奖情况有________种.(用数字作答)
答案 60
解析 一、二、三等奖,三个人获得,有A=24(种).
一、二、三等奖,有一个人获得2张,一个人获得1张,共有CA=36(种),共有24+36=60(种)不同的获奖情况.
16、20个不加区别的小球放入编号为1,2,3的三个盒子中,要求每个盒内的球数不小于它的编号数,则不同的放法种数为________.
答案 120
解析 先在编号为2,3的盒内分别放入1,2个球,还剩17个小球,三个盒内分别至少再放入1个球,将17个球排成一排,有16个空隙,插入2块挡板分为三堆放入三个盒中即可,共C=120(种)方法.
17、已知10件不同产品中有4件是次品,现对它们进行一一测试,直至找出所有4件次品为止.
(1)若恰在第5次测试,才测试到第一件次品,第10次才找到最后一件次品,则这样的不同测试方法数是多少?
(2)若恰在第5次测试后,就找出了所有4件次品,则这样的不同测试方法数是多少?
解 (1)先排前4次测试,只能取正品,有A种不同测试方法,再从4件次品中选2件排在第5和第10的位置上测试,有CA=A(种)测法,再排余下4件的测试位置,有A种测法.
所以共有不同测试方法A·A·A=103 680(种).
(2)第5次测试恰为最后一件次品,另3件在前4次中出现,从而前4次有一件正品出现,所以共有不同测试方法CCA=576(种).
一、排列数及排列数公式
排列数定义 从n个不同元素中取出m(m≤n)个元素的所有不同排列的个数叫做从n个不同元素中取出m个元素的排列数
排列数表示法 A
排列数公式 乘积式 A=n(n-1)(n-2)…(n-m+1)
阶乘式 A=
性质 A=n!,0!=1
备注 n,m∈N*,m≤n
类型一 对排列数定义的理解:更换元素的位置是否影响到结果,有影响的属于排列数
1、判断下列问题是否为排列问题,对的打“√”,错的打“×”
(1)北京、上海、天津三个民航站之间的直达航线的飞机票的价格 ( )
(2)选2个小组分别去植树和种菜 ( )
(3)选2个小组去种菜 ( )
(4)选10人组成一个学习小组 ( )
(5)选3个人分别担任班长、学习委员、生活委员 ( )
(6)某班40名学生在假期相互通信 ( )
解(1)中票价只有三种,虽然机票是不同的,但票价是一样的,不存在顺序问题,所以不是排列问题.
(2)植树和种菜是不同的,存在顺序问题,属于排列问题.
(3)(4)不存在顺序问题,不属于排列问题.
(5)中每个人的职务不同,例如甲当班长或当学习委员是不同的,存在顺序问题,属于排列问题.
(6)A给B写信与B给A写信是不同的,所以存在着顺序问题,属于排列问题.
所以在上述各题中(2)(5)(6)是排列问题,(1)(3)(4)不是排列问题.
类型二 排列数公式及应用:注意选择乘积式还是阶乘式
2、(x-3)(x-4)(x-5)…(x-12)(x-13),x∈N*,x>13可表示为( )
A.A B.A C.A D.A
答案 B
解析 从(x-3),(x-4),…到(x-13)共(x-3)-(x-13)+1=11(个)数,所以根据排列数公式知(x-3)(x-4)(x-5)…(x-12)(x-13)=A.
3、用排列数表示(55-n)(56-n)…(69-n)= (n∈N*且,n<55)
解 因为55-n,56-n,…,69-n中的最大数为69-n,且共有69-n-(55-n)+1=15(个)元素,
所以(55-n)(56-n)…(69-n)=A.
4、计算=
解 ===1.
5、求证:A-A=mA.
解 因为A-A=-=·=·
=m·=mA,所以A-A=mA.
6、解方程A=140A.
解 根据题意,原方程等价于
即
整理得4x2-35x+69=0(x≥3,x∈N*),
解得x=3.
排列的综合应用
类型一 无限制条件的排列问题
注意事项:典型的排列问题,用排列数计算其排列方法数;若不是排列问题,需用计数原理求其方法种数.排列的概念很清楚,要从“n个不同的元素中取出m个元素”.即在排列问题中元素不能重复选取,而在用分步乘法计数原理解决的问题中,元素可以重复选取.
6、有7本不同的书,从中选3本送给3名同学,每人各1本,共有 种不同的送法。
解 从7本不同的书中选3本送给3名同学,相当于从7个元素中任取3个元素的一个排列,所以共有A=7×6×5=210(种)不同的送法.
7、有7种不同的书,要买3本送给3名同学,每人各1本,共有 种不同的送法。
解 从7种不同的书中买3本书,这3本书并不要求都不相同,根据分步乘法计数原理,共有7×7×7=343(种)不同的送法.
8、有5个不同的科研小课题,从中选3个由高二(6)班的3个学习兴趣小组进行研究,每组一个课题,
共有 种不同的安排方法。
解 从5个不同的课题中选出3个,由兴趣小组进行研究,对应于从5个不同元素中取出3个元素的一个排列,因此不同的安排方法有A=5×4×3=60(种).
9、有5个不同的科研小课题,高二(6)班的3个学习兴趣小组报名参加,每组限报一个课题,共有 种不同的报名方法。
解 由题意知3个兴趣小组可能报同一科研课题,因此元素可以重复,不是排列问题.
由于每个兴趣小组都有5种不同的选择,且3个小组都选择完才算完成这件事,所以由分步乘法计数原理得共有5×5×5=125(种)报名方法.
类型二 排队问题
解题原则:“处理元素“相邻”“不相邻”问题应遵循“先整体,后局部”的原则.
解题方法:①元素相邻问题,一般用“捆绑法”,先把相邻的若干个元素“捆绑”为一个大元素与其余元素全排列,然后再松绑,将这若干个元素内部全排列.
②元素不相邻问题,一般用“插空法”,先将不相邻元素以外的“普通”元素全排列,然后在“普通”元素之间及两端插入不相邻元素.
10、5位母亲带领5名儿童站成一排照相,儿童不相邻的站法有________种.(可用排列数表示)
答案 86400
解析 第1步,先排5位母亲的位置,有A种排法;
第2步,把5名儿童插入5位母亲所形成的6个空位中,如下所示:
母亲____母亲____母亲____母亲____母亲____,共有A种排法.
由分步乘法计数原理可知,符合条件的站法共有A·A=86 400(种).
11、两家夫妇各带一个小孩一起去公园游玩,购票后排队依次入园.为安全起见,首尾一定要排两位爸爸,另外,两个小孩一定要排在一起,则这6人的入园顺序排法种数为________.
答案 24
解析 分3步进行分析,
①先安排两位爸爸,必须一首一尾,有A=2(种)排法,
②两个小孩一定要排在一起,将其看成一个元素,考虑其顺序有A=2(种)排法,
③将两个小孩看作一个元素与两位妈妈进行全排列,有A=6(种)排法.则共有2×2×6=24(种)排法.
12、3名男生、4名女生按照不同的要求排队,求不同的排队方法的种数.
(1)全体站成一排,男、女各站在一起;
(2)全体站成一排,男生必须站在一起;
(3)全体站成一排,男生不能站在一起;
(4)全体站成一排,男、女各不相邻.
解 (1)男生必须站在一起是男生的全排列,有A种排法;
女生必须站在一起是女生的全排列,有A种排法;
全体男生、女生各视为一个元素,有A种排法.
由分步乘法计数原理知,共有A·A·A=288(种)排队方法.
(2)三个男生全排列有A种方法,把所有男生视为一个元素,与4名女生组成5个元素全排列,有A种排法.故有A·A=720(种)排队方法.
(3)先安排女生,共有A种排法;男生在4个女生隔成的五个空中安排,共有A种排法,故共有A·A=1 440(种)排法.
(4)排好男生后让女生插空,共有A·A=144(种)排法.
13、某次文艺晚会上共演出8个节目,其中2个唱歌、3个舞蹈、3个曲艺节目,求分别满足下列条件的节目编排方法有多少种?
(1)一个唱歌节目开头,另一个放在最后压台;
(2)2个唱歌节目互不相邻;
(3)2个唱歌节目相邻且3个舞蹈节目不相邻.
解 (1)先排唱歌节目有A种排法,再排其他节目有A种排法,所以共有A·A=1 440(种)排法.
(2)先排3个舞蹈节目和3个曲艺节目有A种排法,再从其中7个空(包括两端)中选2个排唱歌节目,有A种插入方法,所以共有A·A=30 240(种)排法.
(3)把2个相邻的唱歌节目看作一个元素,与3个曲艺节目排列共A种排法,再将3个舞蹈节目插入,共有A种插入方法,最后将2个唱歌节目互换位置,有A种排法,故所求排法共有A·A·A=2 880(种)排法.
解题原则:解“在”与“不在”的有限制条件的排列问题时,可以从元素入手也可以从位置入手,原则是谁特殊谁优先.
解题方法:从元素入手时,先给特殊元素安排位置,再把其他元素安排在其他位置上,从位置入手时,先安排特殊位置,再安排其他位置.
易错提醒:解题时,或从元素考虑,或从位置考虑,都要贯彻到底.不能一会考虑元素,一会考虑位置,造成分类、分步混乱,导致解题错误.
14、6位选手依次演讲,其中选手甲不排在第一个也不排在最后一个演讲,则不同的演讲次序共有( )
A.240种 B.360种 C.480种 D.720种
答案 C
解析 第一步:排甲,共有A种不同的排法;第二步:排其他人,共有A种不同的排法,因此不同的演讲次序共有AA=480(种).
15、某单位安排7位员工在10月1日至7日值班,每天安排1人,每人值班1天.若7位员工中的甲、乙被安排在相邻两天值班,丙不在10月1日值班,丁不在10月7日值班,则不同的安排方案共有( )
A.504种 B.960种 C.1108种 D.1008种
答案 D
解析 由题意知,满足甲、乙两人被安排在相邻两天值班的方案共有AA=1 440(种),其中满足甲、乙两人被安排在相邻两天值班且丙在10月1日值班的方案共有AA=240(种),满足甲、乙两人被安排在相邻两天值班且丁在10月7日值班的方案共有AA=240(种),满足甲、乙两人安排在相邻两天值班且丙在10月1日值班、丁在10月7日值班的方案共有AA=48(种).因此满足题意的方案共有1 440-2×240+48=1008(种).
16、某一天的课程表要排入政治、语文、数学、物理、体育、美术共六节课,如果第一节不排体育,最后一节不排数学,那么共有 种不同的排课程表的方法。
解 6门课总的排法是A,其中不符合要求的可分为体育排在第一节,有A种排法;数学排在最后一节,有A种排法,但这两种方法,都包括体育排在第一节,数学排在最后一节,这种情况有A种排法.因此符合条件的排法有A-2A+A=504(种).
17、六人按下列要求站一横排,分别有多少种不同的站法?
(1)甲不能在两端;
(2)甲、乙必须在两端;
(3)甲不在最左端,乙不在最右端.
解 (1)先考虑甲有A种方案,再考虑其余5人全排列,故N=A·A=480(种);
(2)先安排甲、乙有A种方案,再安排其余4人全排列,故N=A·A=48(种);
(3)方法一 甲在最左端的站法有A种,乙在最右端的站法有A种,且甲在最左端而乙在最右端的站法有A种,共有A-2A+A=504(种)站法.
方法二 以元素甲分类可分为两类:a.甲站最右端有A种,b.甲在中间4个位置之一,而乙不在最右端有A·A·A种,故共有A+A·A·A=504(种)站法.
在有些排列问题中,某些元素有前后顺序是确定的(不一定相邻),解决这类问题的基本方法有两种:
①整体法:即若有m+n个元素排成一列,其中m个元素之间的先后顺序确定不变,先将这m+n个元素排成一列,有A种不同的排法;然后任取一个排列,固定其他n个元素的位置不动,把这m个元素交换顺序,有A种排法,其中只有一个排列是我们需要的,因此共有种满足条件的不同排法.
②插空法:即m个元素之间的先后顺序确定不变,因此先排这m个元素,只有一种排法,然后把剩下的n个元素分类或分步插入由以上m个元素形成的空隙中.
18、将A,B,C,D,E这5个字母排成一列,要求A,B,C在排列中的顺序为“A,B,C”或“C,B,A”(可以不相邻).则有 种不同的排列方法。
解 5个不同元素中部分元素A,B,C的排列顺序已定,这种问题有以下两种常用的解法.
方法一 (整体法)5个元素无约束条件的全排列有A种,由于字母A,B,C的排列顺序为“A,B,C”或“C,B,A”,因此,在上述的全排列中恰好符合“A,B,C”或“C,B,A”排列方式的排列有×2=40(种).
方法二 (插空法)若字母A,B,C的排列顺序为“A,B,C”,将字母D,E插入,这时形成的4个空中,分两类:
第一类,若字母D,E相邻,则有A·A种排法;
第二类,若字母D,E不相邻,则有A种排法.
所以有A·A+A=20(种)不同的排列方法.
同理,若字母A,B,C的排列顺序为“C,B,A”,也有20种不同的排列方法.
因此,满足条件的排列有20+20=40(种).
19、用1,2,3,4,5,6,7组成没有重复数字的七位数,若1,3,5,7的顺序一定,则有________个七位数符合条件.
答案 210
解析 若1,3,5,7的顺序不定,有A=24(种)排法,故1,3,5,7的顺序一定的排法数只占总排法数的.
故有A=210(个)七位数符合条件.
类型三 数字排列问题
数字排列的常见特殊性:(1)首位不能为0;(2)有无重复数字;(3)奇偶数;(4)某数的倍数;(5)大于(或小于)某数.
20、用0,1,2,3,4,5这六个数字可以组成多少个符合下列条件的无重复的数字?
(1)六位奇数;
(2)个位数字不是5的六位数;
(3)不大于4310的四位偶数.
解 (1)第一步,排个位,有A种排法;
第二步,排十万位,有A种排法;
第三步,排其他位,有A种排法.
故共有AAA=288(个)六位奇数.
(2)方法一 (直接法):
十万位数字的排法因个位上排0与不排0而有所不同,因此需分两类.
第一类,当个位排0时,有A个;
第二类,当个位不排0时,有AAA个.
故符合题意的六位数共有A+AAA=504(个).
方法二 (排除法):
0在十万位和5在个位的排列都不对应符合题意的六位数,这两类排列中都含有0在十万位和5在个位的情况.
故符合题意的六位数共有A-2A+A=504(个).
(3)分三种情况,具体如下:
①当千位上排1,3时,有AAA个.
②当千位上排2时,有AA个.
③当千位上排4时,形如4 0×2,4 2×0的各有A个;
形如4 1××的有AA个;
形如4 3××的只有4 310和4 302这两个数.
故共有AAA+AA+2A+AA+2=110(个).
21、用0,1,2,3,4,5这六个数字可以组成多少个无重复数字的
(1)能被5整除的五位数;
(2)能被3整除的五位数;
(3)若所有的六位数按从小到大的顺序组成一个数列{an},则240135是第几项.
解 (1)个位上的数字必须是0或5.个位上是0,有A个;个位上是5,若不含0,则有A个;若含0,但0不作首位,则0的位置有A种排法,其余各位有A种排法,故共有A+A+AA=216(个)能被5整除的五位数.
(2)能被3整除的条件是各位数字之和能被3整除,则5个数可能有{1,2,3,4,5}和{0,1,2,4,5}两种情况,能够组成的五位数分别有A个和AA个.
故能被3整除的五位数有A+AA=216(个).
(3)由于是六位数,首位数字不能为0,首位数字为1有A个数,首位数字为2,万位上为0,1,3中的一个,有3A个数,
∴240 135的项数是A+3A+1=193,
即240135是数列的第193项.
三、组合数与组合数公式
组合数定义及表示 从n个不同元素中取出m(m≤n)个元素的所有不同组合的个数,叫做从n个不同元素中取出m个元素的组合数,用符号C表示.
组合数公式 乘积形式 C=
阶乘形式 C=
性质 C=C C=C+C
备注 规定C=1
类型一 组合概念的理解
排列与组合的区别:区分排列与组合的办法是首先弄清楚事件是什么,区分的标志是有无顺序,而区分有无顺序的方法是:把问题的一个选择结果写出来,然后交换这个结果中任意两个元素的位置,看是否产生新的变化,若有新变化,即说明有顺序,是排列问题;若无新变化,即说明无顺序,是组合问题.
22、判断下列问题是排列还是组合问题,排列打“√”,组合打“×”
(1)a,b,c,d四支足球队之间进行单循环比赛,共需比赛多少场 。 ( )
(2)a,b,c,d四支足球队争夺冠、亚军,有多少种不同的结果 。 ( )
(3)从全班40人中选出3人分别担任班长、副班长、学习委员三个职务,有多少种不同的选法 ( )
(4)从全班40人中选出3人参加某项活动,有多少种不同的选法 ( )
解 (1)单循环比赛要求两支球队之间只打一场比赛,没有顺序,是组合问题.
(2)冠、亚军是有顺序的,是排列问题.
(3)3人分别担任三个不同职务,有顺序,是排列问题.
(4)3人参加某项相同活动,没有顺序,是组合问题.
类型二 组合数公式及性质的应用
注意运用一下技巧:
(1)涉及具体数字的可以直接用公式C==计算.
(2)涉及字母的可以用阶乘式C=计算.
(3)计算时应注意利用组合数的两个性质:
①C=C;②C=C+C.
23、计算C+C+C+…+C的值为( )
A.C B.C
C.C-1 D.C-1
解析 C+C+C+…+C=C+C+C+C+…+C-C=C+C+…+C-1=…
=C+C-1=C-1.
24、计算C+C=________.
解析 C+C=C+C=+200=5150.
25、计算C-C·A=
解 原式=C-A=-7×6×5=210-210=0.
26、求证:C=C.
证明 因为右边=C=·==C,
左边=C,所以左边=右边,所以原式成立.
27、已知-=,求C+C
解 (1)∵-=,
∴-=,
即-
=.
∴1-=,
即m2-23m+42=0,解得m=2或21.
∵0≤m≤5,∴m=2,
∴C+C=C+C=C=84.
28、解不等式C>C.
(2)由C>C,得
即解得
又n∈N*,∴该不等式的解集为{6,7,8,9}.
29、解方程3C=5A.
解 原式可变形为3C=5A,
即
=5(x-4)(x-5),
所以(x-3)(x-6)=5×4×2=8×5.
所以x=11或x=-2(舍去).
经检验符合题意,所以方程的解为x=11.
四、组合的综合应用
类型一 简单的组合问题(无限制的组合问题)
①解简单的组合应用题时,首先要判断它是不是组合问题,组合问题与排列问题的根本区别在于排列问题与取出元素之间的顺序有关,而组合问题与取出元素的顺序无关.
②要注意两个基本原理的运用,即分类与分步的灵活运用.
在分类和分步时,一定注意有无重复或遗漏.
30、有10名教师,其中6名男教师,4名女教师.
(1)现要从中选2名去参加会议,有________种不同的选法;
(2)选出2名男教师或2名女教师参加会议,有________种不同的选法;
(3)现要从中选出男、女教师各2名去参加会议,有________种不同的选法.
答案 (1)45 (2)21 (3)90
解析 (1)从10名教师中选2名去参加会议的选法种数,就是从10个不同元素中取出2个元素的组合数,即C==45(种).
(2)可把问题分两类情况:
第1类,选出的2名是男教师有C种方法;
第2类,选出的2名是女教师有C种方法.
根据分类加法计算原理,共有C+C=15+6=21(种)不同选法.
(3)从6名男教师中选2名的选法有C种,从4名女教师中选2名的选法有C种,根据分步乘法计数原理,共有不同的选法C×C=×=90(种).
31、一个口袋内装有大小相同的7个白球和1个黑球.
(1)从口袋内取出的3个小球,共有 种取法?
(2)从口袋内取出3个球,使其中含有1个黑球,有 种取法?
(3)从口袋内取出3个球,使其中不含黑球,有 种取法?
解 (1)从口袋内的8个球中取出3个球,
取法种数是C==56.
(2)从口袋内取出3个球有1个是黑球,于是还要从7个白球中再取出2个,取法种数是C==21.
(3)由于所取出的3个球中不含黑球,也就是要从7个白球中取出3个球,取法种数是C==35.
类型二 有限制条件的组合问题
常考的两类问题:
①“含”与“不含”问题,其解法常用直接分步法,即“含”的先取出,“不含”的可把所指元素去掉再取,分步计数;
②“至多”“至少”问题,其解法常有两种解决思路:一是直接分类法,但要注意分类要不重不漏;二是间接法,注意找准对立面,确保不重不漏.
32、某食堂每天中午准备4种不同的荤菜,7种不同的蔬菜,用餐者可以按下述方法之一搭配午餐:(1)任选两种荤菜、两种蔬菜和白米饭;(2)任选一种荤菜、两种蔬菜和蛋炒饭.则每天不同午餐的搭配方法共有( )
A.210种 B.420种 C.56种 D.22种
答案 A
解析 由分类加法计数原理知,两类配餐的搭配方法之和即为所求,所以每天不同午餐的搭配方法共有CC+CC=210(种).
33、某乒乓球队有9名队员,其中2名是种子选手,现在挑选5名选手参加比赛,种子选手必须在内,那么不同选法共有( )
A.26种 B.84种 C.35种 D.21种
答案 C
解析 从7名队员中选出3人有C==35(种)选法.
34、身高各不相同的7名同学排成一排照相,要求正中间的同学最高,左右两边分别顺次一个比一个低,这样的排法种数是( )
A.5 040 B.36 C.18 D.20
答案 D
解析 最高的同学站中间,从余下6人中选3人在一侧只有一种站法,另3人在另一侧也只有一种站法,所以排法有C=20(种).
35、课外活动小组共13人,其中男生8人,女生5人,并且男、女生各有一名队长,现从中选5人主持某项活动,依下列条件各有多少种选法?
(1)至少有一名队长当选;
(2)至多有两名女生当选;
(3)既要有队长,又要有女生当选.
解 (1)C-C=825(种)
(2)至多有2名女生当选含有三类:
有2名女生;只有1名女生;没有女生,
所以共有CC+CC+C=966(种)选法.
(3)分两类:
第一类女队长当选,有C=495(种)选法,
第二类女队长没当选,有CC+CC+CC+C=295(种)选法,
所以共有495+295=790(种)选法.
类型三 分组、分配问题
易错点:遇到平均分成m组的情况,需要除掉
36、江西省旅游产业发展大会于2020年6月11日~13日在赣州举行,某旅游公司为推出新的旅游项目,特派出五名工作人员前往赣州三个景点进行团队游的可行性调研.若每名工作人员只去一个景点且每个景点至少有一名工作人员前往,则不同的人员分配方案种数为( )
A.60 B.90 C.150 D.240
【答案】C
【解析】根据题意,分2步进行分析:
①将五名工作人员分成3组,
若分为3、1、1的三组,有种分法,
若分为2、2、1的三组,种分法,
则有种分组分法;
②将分好的三组全排列,对应三个景点,有种情况,
则有种分配方法;
故选:.
37、疫情期间,上海某医院安排5名专家到3个不同的区级医院支援,每名专家只去一个区级医院,每个区级医院至少安排一名专家,则不同的安排方法共有( )
A.60种 B.90种 C.150种 D.240种
【答案】C
【解析】5名专家到3个不同的区级医院,分为1,2,2和1,1,3两种情况;
分为1,2,2时安排有;分为1,1,3时安排有
所以一共有
38、据《孙子算经》中记载,中国古代诸侯的等级从低到高分为:男、子、伯、侯、公,共五级,若给获得巨大贡献的7人进行封爵,要求每个等级至少有一人,至多有两人,则伯爵恰有两人的概率为( )
A. B. C. D.
【答案】B
【解析】人进行封爵,每个等级至少一人,至多两人,则共有种分法;
其中伯爵恰有两人的分法有种分法,
伯爵恰有两人的概率
39、2020年是我国脱贫攻坚决战决胜之年,某县农业局为支持该县的扶贫工作,决定派出8名农技人员(5男3女),并分成两组,分配到2个贫困村进行扶贫工作,若每组至少3人,且每组都有男农技人员,则不同的分配方案共有______种(用数字填写答案).
【答案】180
【解析】分配的方案有两类,
第一类:一组3人,另一组5人,有种;
第二类:两组均为4人,有种,
所以共有种不同的分配方案.
40、6本不同的书,分为3组,在下列条件下各有多少种不同的分配方法?
(1)每组2本(平均分组);
(2)一组1本,一组2本,一组3本(不平均分组);
(3)一组4本,另外两组各1本(局部平均分组).
解 (1)每组2本,均分为3组的方法数为==15.
(2)一组1本,一组2本,一组3本的分组种数为CCC=20×3=60.
(3)一组4本,另外两组各1本的分组种数为==15.
41、6本不同的书,分给甲、乙、丙3人,在下列条件下各有多少种不同的分配方法?
(1)甲2本,乙2本,丙2本;
(2)甲1本,乙2本,丙3本;
(3)甲4本,乙、丙每人1本;
(4)每人2本;
(5)一人1本,一人2本,一人3本;
(6)一人4本,其余两人每人1本.
解 (1)(2)(3)中,由于每人分的本数固定,属于定向分配问题,由分步乘法计数原理得:
(1)共有CCC=90(种)不同的分配方法;
(2)共有CCC=60(种)不同的分配方法;
(3)共有CCC=30(种)不同的分配方法.
(4)(5)(6)属于不定向分配问题,是该类题中比较困难的问题.分配给3人,同一本书给不同的人是不同的分法,属于排列问题.实际上可看作两个步骤:先分为3组,再把这3组分给甲、乙、丙3人的全排列数A即可.因此,(4)共有CCC÷A×A=90(种)不同的分配方法;
(5)共有CCC×A=360(种)不同的分配方法;
(6)共有CCC÷A×A=90(种)不同的分配方法.
相同元素分配问题的处理策略
(1)隔板法:如果将放有小球的盒子紧挨着成一行放置,便可看作在排成一行的小球的空隙中插入了若干隔板,相邻两块隔板形成一个“盒”.每一种插入隔板的方法对应着小球放入盒子的一种方法,此法称之为隔板法.隔板法专门解决相同元素的分配问题.
(2)将n个相同的元素分给m个不同的对象(n≥m),有C种方法.可描述为n-1个空中插入m-1块板.
42、某同学有同样的画册2本,同样的集邮册3本,从中取出4本赠送给4位朋友,每位朋友1本,则不同的赠送方法共有( )
A.4种 B.10种
C.18种 D.20种
答案 B
解析 由于只剩一本书,且这些画册、集邮册分别相同,可以从剩余的书的类别进行分析.又由于排列、组合针对的是不同的元素,应从4位朋友中进行选取.
第一类:当剩余的一本是画册时,相当于把3本相同的集邮册和1本画册分给4位朋友,只有1位朋友得到画册.即把4位朋友分成人数为1,3的两队,有1个元素的那队分给画册,另一队分给集邮册,有C种分法.
第二类:当剩余的一本是集邮册时,相当于把2本相同的画册和2本相同的集邮册分给4位朋友,有2位朋友得到画册,即把4位朋友分成人数为2,2的两队,一队分给画册,另一队分给集邮册,有C种分法.
因此,满足题意的赠送方法共有C+C=4+6=10(种).
43、假如北京大学给中山市某三所重点中学7个自主招生的推荐名额,则每所中学至少分到一个名额的方法数为( )
A.30 B.21 C.10 D.15
考点 排列组合综合问题
题点 分组分配问题
答案 D
解析 用“隔板法”.在7个名额中间的6个空位上选2个位置加2个隔板,有C=15(种)分配方法.
44、将6个相同的小球放入4个编号为1,2,3,4的盒子,求下列方法的种数.
(1)每个盒子都不空;
(2)恰有一个空盒子;
(3)恰有两个空盒子.
解 (1)先把6个相同的小球排成一行,在首尾两球外侧放置一块隔板,然后在小球之间5个空隙中任选3个空隙各插一块隔板,有C=10(种).
(2)恰有一个空盒子,插板分两步进行.先在首尾两球外侧放置一块隔板,并在5个空隙中任选2个空隙各插一块隔板,如|0|000|00|,有C种插法,然后将剩下的一块隔板与前面任意一块并放形成空盒,如|0|000||00|,有C种插法,故共有C·C=40(种).
(3)恰有两个空盒子,插板分两步进行.
先在首尾两球外侧放置一块隔板,并在5个空隙中任选1个空隙各插一块隔板,有C种插法,如|00|0000|,然后将剩下的两块隔板插入形成空盒.
①这两块板与前面三块板形成不相邻的两个盒子,
如||00||0000|,有C种插法.
②将两块板与前面三块板之一并放,如|00|||0000|,有C种插法.
故共有C·(C+C)=30(种).
课后巩固练习
1、某电视台一节目收视率很高,现要连续插播4个广告,其中2个不同的商业广告和2个不同的公益宣传广告,要求最后播放的必须是商业广告,且2个商业广告不能连续播放,则不同的播放方式有( )
A.8种 B.16种 C.18种 D.24种
答案 A
解析 可分三步:第一步,排最后一个商业广告,有A种;第二步,在前两个位置选一个排第二个商业广告,有A种;第三步,余下的两个位置排公益宣传广告,有A种.根据分步乘法计数原理,不同的播放方式共有A·A·A=8(种),故选A.
2、由1,2,3,4,5组成没有重复数字的四位数,按从小到大的顺序排成一个数列{an},则a72等于( )
A.1543 B.2543 C.3542 D.4532
答案 C
解析 首位是1的四位数有A=24(个),
首位是2的四位数有A=24(个),首位是3的四位数有A=24(个),
由分类加法计数原理得,
首位小于4的所有四位数共3×24=72(个).由此得a72=3 542.
3、若从1,2,3,…,9这9个整数中同时取3个不同的数,使其和为奇数,则不同的取法共有( )
A.30种 B.33种 C.37种 D.40种
答案 D
解析 从1,2,3,…,9这9个数中取出3个不同的数,使其和为奇数的情况包括:(1)取出的3个数都是奇数,取法有C=10(种);(2)取出的3个数中有2个偶数、1个奇数,取法有CC=30(种),根据分类加法计数原理,满足题意的取法共有10+30=40(种).
4、某班级要从4名男生、2名女生中选派4人参加某次社区服务,如果要求至少有1名女生,那么不同的选派方案种数为( )
A.24种 B.14种 C.28种 D.48种
答案 B
解析 方法一 分两类完成:
第1类,选派1名女生、3名男生,有C·C种选派方案;
第2类,选派2名女生、2名男生,有C·C种选派方案.
故共有C·C+C·C=14(种)不同的选派方案.
方法二 6人中选派4人的组合数为C,其中都选男生的组合数为C,所以至少有1名女生的选派方案有C-C=14(种).
5、由数字0,1,2,3,4,5组成没有重复数字的六位数,其中个位数字小于十位数字的共有( )
A.210个 B.300个 C.464个 D.600个
答案 B
解析 由于组成没有重复数字的六位数,个位小于十位的与个位大于十位的一样多,故有=300(个).
6、从乒乓球运动员男5名、女6名中组织一场混合双打比赛,不同的组合方法有( )
A.CC种 B.CA种
C.CACA种 D.AA种
答案 B
解析 先从5名男选手中任意选取2名,有C种选法,再从6名女选手中任意选择两名与选出的男选手打比赛,有CA,即A种.所以共有CA种.
7、将标号为A,B,C,D,E,F的6张卡片放入3个不同的信封中,若每个信封放2张卡片,其中标号为A,B的卡片放入同1个信封,则不同的放法共有( )
A.12种 B.18种 C.36种 D.54种
答案 B
解析 由题意知,不同的放法共有CC=3×=18(种).
8、某地招募了20名志愿者,他们编号分别为1号,2号,…,19号,20号,如果要从中任意选取4人再按编号大小分成两组去做一些预备服务工作,其中两个编号较小的人在一组,两个编号较大的人在另一组,那么确保5号与14号入选并被分配到同一组的选取种数是( )
A.16 B.21 C.24 D.90
答案 B
解析 分2类:
第1类,5号与14号为编号较大的一组,则另一组编号较小的有C=6(种)选取方法.
第2类,5号与14号为编号较小的一组,则编号较大的一组有C=15(种)选取方法.
由分类加法计数原理得,共有C+C=6+15=21(种)选取方法.
9、.北京《财富》全球论坛期间,某高校有14名志愿者参加接待工作,若每天早、中、晚三班,每班4人,每人每天最多值一班,则开幕式当天不同的排班种数为( )
A.CCC B.CAA
C. D.CCCA
答案 A
解析 首先从14人中选出12人共C种,然后将12人平均分为3组共种,然后这两步相乘,得.将三组分配下去共C·C·C种.故选A.
10、在制作飞机的某一零件时,要先后实施6个工序,其中工序A只能出现在第一步或最后一步,工序B和C在实施时必须相邻,则实施顺序的编排方法共有( )
A.34种 B.48种 C.96种 D.144种
答案 C
解析 由题意可知,先排工序A,有2种编排方法;再将工序B和C视为一个整体(有2种顺序)与其他3个工序全排列共有2A种编排方法.故实施顺序的编排方法共有2×2A=96(种).故选C.
11、从6名短跑运动员中选出4人参加4×100 m接力赛,甲不能跑第一棒和第四棒,问共有________种参赛方案.
答案 240
解析 方法一 从人(元素)的角度考虑,优先考虑甲,分以下两类:
第1类,甲不参赛,有A种参赛方案;
第2类,甲参赛,可优先将甲安排在第二棒或第三棒,有2种方法,然后安排其他3棒,有A种方法,此时有2A种参赛方案.
由分类加法计数原理可知,甲不能跑第一棒和第四棒的参赛方案共有A+2A=240(种).
方法二 从位置(元素)的角度考虑,优先考虑第一棒和第四棒,则这两棒可以从除甲之外的5人中选2人,有A种方法;其余两棒从剩余4人中选,有A种方法.
由分步乘法计数原理可知,甲不能跑第一棒和第四棒的参赛方案共有AA=240(种).
方法三 (排除法):不考虑甲的约束,6个人占4个位置,有A种安排方法,剔除甲跑第一棒和第四棒的参赛方案有2A种,所以甲不能跑第一棒和第四棒的参赛方案共有A-2A=240(种).
12、六个停车位置,有3辆汽车需要停放,若要使三个空位连在一起,则停放的方法数为________.
答案 24
解析 把3个空位看作一个元素,与3辆汽车共有4个元素全排列,故停放的方法有A=4×3×2×1=24(种).
13、在2017年的上海高考改革方案中,要求每位考生必须在物理、化学、生物、政治、历史、地理6门学科中选择3门学科参加等级考试.小明同学决定在生物、政治、历史三门中至多选择一门,那么小明同学的选择方案有________种.
答案 10
解析 ①在生物、政治、历史三门中选择1门,则在物理、化学、地理中选2门,有CC=9(种)选法;
②在生物、政治、历史三门中选择0门,则物理、化学、地理全选,有C=1(种)选法.
共有选法9+1=10(种).
14、如图所示的几何体是由一个正三棱锥P-ABC与正三棱柱ABC-A1B1C1组合而成,现用3种不同颜色对这个几何体的表面涂色(底面A1B1C1不涂色),要求相邻的面均不同色,则不同的涂色方案共有______种.
答案 12
解析 先涂三棱锥P-ABC的三个侧面,然后涂三棱柱的三个侧面,共有C×C×C×C=3×2×1×2=12(种)不同的涂法.
15、在8张奖券中有一、二、三等奖各1张,其余5张无奖.将这8张奖券分配给4个人,每人2张,不同的获奖情况有________种.(用数字作答)
答案 60
解析 一、二、三等奖,三个人获得,有A=24(种).
一、二、三等奖,有一个人获得2张,一个人获得1张,共有CA=36(种),共有24+36=60(种)不同的获奖情况.
16、20个不加区别的小球放入编号为1,2,3的三个盒子中,要求每个盒内的球数不小于它的编号数,则不同的放法种数为________.
答案 120
解析 先在编号为2,3的盒内分别放入1,2个球,还剩17个小球,三个盒内分别至少再放入1个球,将17个球排成一排,有16个空隙,插入2块挡板分为三堆放入三个盒中即可,共C=120(种)方法.
17、已知10件不同产品中有4件是次品,现对它们进行一一测试,直至找出所有4件次品为止.
(1)若恰在第5次测试,才测试到第一件次品,第10次才找到最后一件次品,则这样的不同测试方法数是多少?
(2)若恰在第5次测试后,就找出了所有4件次品,则这样的不同测试方法数是多少?
解 (1)先排前4次测试,只能取正品,有A种不同测试方法,再从4件次品中选2件排在第5和第10的位置上测试,有CA=A(种)测法,再排余下4件的测试位置,有A种测法.
所以共有不同测试方法A·A·A=103 680(种).
(2)第5次测试恰为最后一件次品,另3件在前4次中出现,从而前4次有一件正品出现,所以共有不同测试方法CCA=576(种).
