24.1.4 圆周角第二课时
文档属性
| 名称 | 24.1.4 圆周角第二课时 |  | |
| 格式 | zip | ||
| 文件大小 | 46.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-06 22:15:32 | ||
图片预览


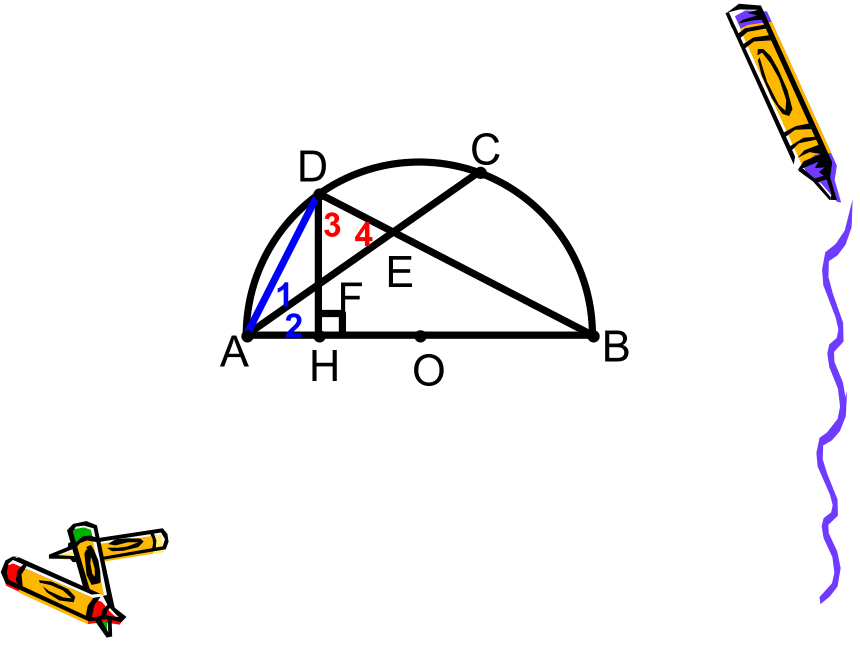
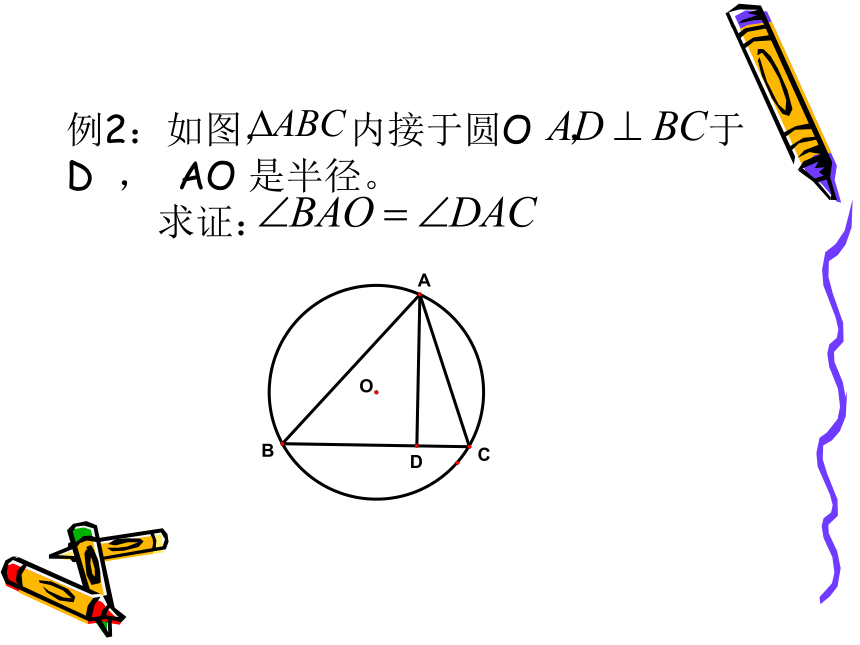
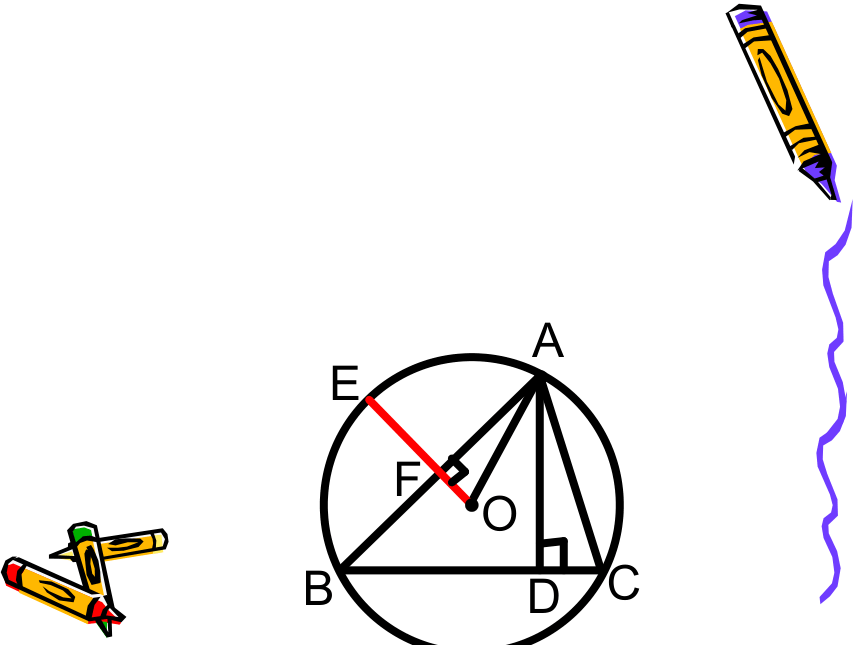

文档简介
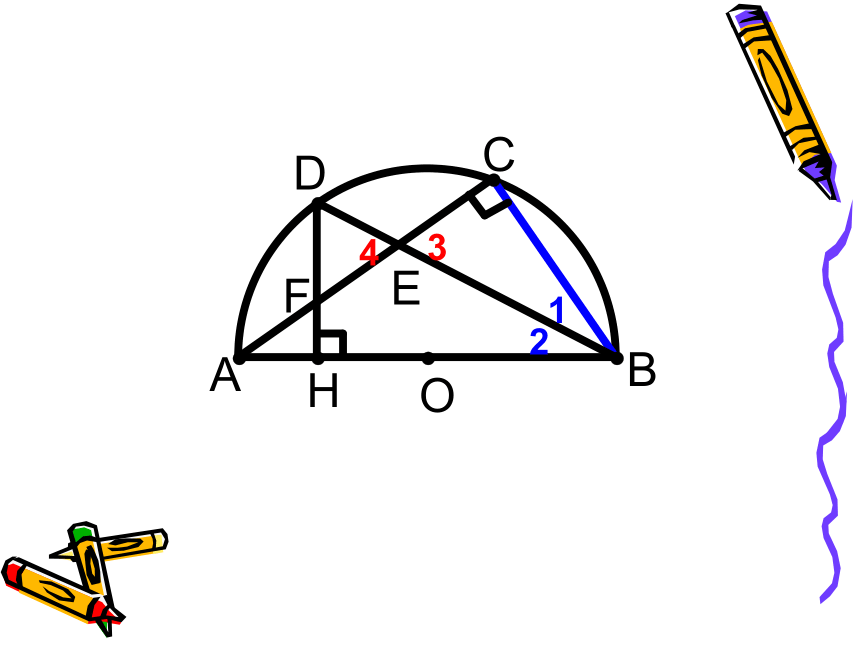
课件26张PPT。24.1.4 圆周角第二课时例1: 如图, 是半圆的直径, 于 ,弦 交 于 ,交半圆于 点,若 。
求证:C是弧AF的中点
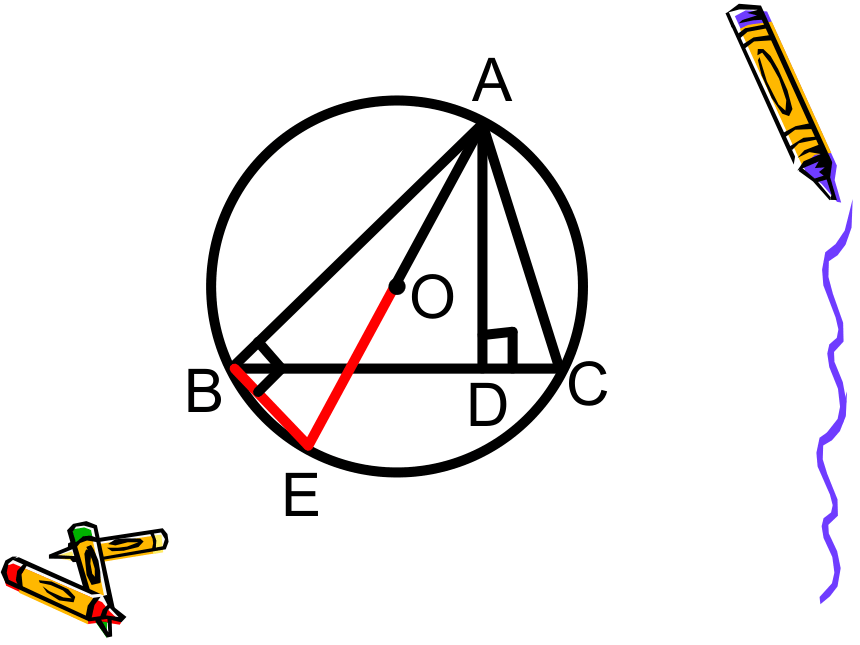
E例2:如图, 内接于圆O , 于 D , AO 是半径。
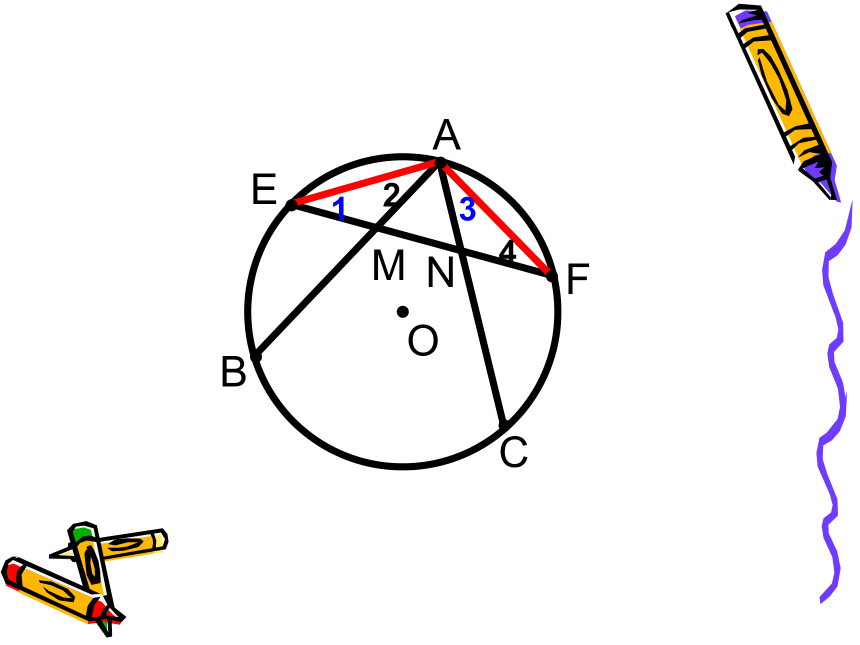
求证:例3已知: 如图,⊙O中,AB﹑AC是弦,
E﹑F分别为弧AB﹑弧AC的中点,
求证: AM=AN圆内角问题:(可推广)
把一个圆内角,根据三角形的外角知识,用两个圆周角的和来表示,进而在圆周角的知识平台上研究问题.
例4、如图, ΔABC是⊙O的内接三角形,AD平分∠BAC交圆于D,CE平分∠ACB交AD于E,连接BD.
求证:BD=ED.
例5、如图,已知AB是⊙O的直径,弦CD⊥AB于E,F是AC上的点,
AF的延长线交DC的延长线于G,
求证:∠AFD=∠GFC.
例6、如图,△ABC内接于⊙O,
过O点作EO⊥BC, 交BA延长线
于E点,交AC于D点,
求证:AD?DC=OD?DE.例7、如图、A、B、C三点在⊙O上,AD是直径,CE⊥AD于点E,CE的延长线交AB于F,
求证:∠ABC=∠ACF.例8、(1)如图1,直线MN与⊙O相交,且与⊙O的直径AB垂直,垂足为P,过点P的直线与⊙O交于C、D两点,直线AC交MN于点E,直线AD交MN于点F.
求证:PC·PD=PE·PF(2)如图2,若直线MN与⊙O相离,(1)中的其余条件不变,那么(1)中的结论还成立吗?
若成立,请给予证明;
若不成立,
请说明理由.(3)在图(3)中,直线MN与⊙O相离,且与⊙O的直径AB垂直,垂足为P,
①请按要求画出图形:画⊙O的割线PCD(PC〈PD),直线BC与MN交于E,
直线BD与MN交于F.
②能否仍能得到
(1)中的结论?
请说明理由.
求证:C是弧AF的中点
E例2:如图, 内接于圆O , 于 D , AO 是半径。
求证:例3已知: 如图,⊙O中,AB﹑AC是弦,
E﹑F分别为弧AB﹑弧AC的中点,
求证: AM=AN圆内角问题:(可推广)
把一个圆内角,根据三角形的外角知识,用两个圆周角的和来表示,进而在圆周角的知识平台上研究问题.
例4、如图, ΔABC是⊙O的内接三角形,AD平分∠BAC交圆于D,CE平分∠ACB交AD于E,连接BD.
求证:BD=ED.
例5、如图,已知AB是⊙O的直径,弦CD⊥AB于E,F是AC上的点,
AF的延长线交DC的延长线于G,
求证:∠AFD=∠GFC.
例6、如图,△ABC内接于⊙O,
过O点作EO⊥BC, 交BA延长线
于E点,交AC于D点,
求证:AD?DC=OD?DE.例7、如图、A、B、C三点在⊙O上,AD是直径,CE⊥AD于点E,CE的延长线交AB于F,
求证:∠ABC=∠ACF.例8、(1)如图1,直线MN与⊙O相交,且与⊙O的直径AB垂直,垂足为P,过点P的直线与⊙O交于C、D两点,直线AC交MN于点E,直线AD交MN于点F.
求证:PC·PD=PE·PF(2)如图2,若直线MN与⊙O相离,(1)中的其余条件不变,那么(1)中的结论还成立吗?
若成立,请给予证明;
若不成立,
请说明理由.(3)在图(3)中,直线MN与⊙O相离,且与⊙O的直径AB垂直,垂足为P,
①请按要求画出图形:画⊙O的割线PCD(PC〈PD),直线BC与MN交于E,
直线BD与MN交于F.
②能否仍能得到
(1)中的结论?
请说明理由.
同课章节目录
