锐角三角全章函数导学案
图片预览



文档简介
9.28.1锐角三角函数(1)导学案
执笔: 初审 : 复审: 王梅
授课人: 课型 :新授 课时:1课时
学生姓名: 班级: 小组:
【教学目标】
初步了解锐角三角函数的意义,初步理解在直角三角形中一个锐角的对边与斜边的比值就是这个锐角的正弦的定义。.
2、会根据已知直角三角形的边长求一个锐角的正弦值。
【教学重点】锐角的正弦的定义。
【教学难点】理解直角三角形中一个锐角与其对边及斜边比值的对应关系。
【导引教学】
【情境导入】
1、如图在Rt△ABC中,∠C=90°,∠A=30°,BC=10m,求AB
2、如图在Rt△ABC中,∠C=90°,∠A=30°,AB=20m,求BC
【自主探究 】
(一)、自学课本P74-76 思考下列问题:
思考1:如果使出水口的高度为50m,那么需要准备多长的水管? ;
如果使出水口的高度为a m,那么需要准备多长的水管? ;
结论:直角三角形中,30°角的对边与斜边的比值是
思考2:在Rt△ABC中,∠C=90°,∠A=45°,∠A对边与斜边
的比值是一个定值吗?如果是,是多少?
结论:直角三角形中,45°角的对边与斜边的比值
思考3:在Rt△ABC中,∠C=90°,∠B=60°,∠B对边与斜边
的比值是一个定值吗?如果是,是多少?
结论:直角三角形中,60°角的对边与斜边的比值
思考4: Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,
∠A=∠A′=a,那么有什么关系.为什么?
结论:这就是说,在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与斜边的比值
5、在Rt△ABC中,∠C=90°,我们把锐角A的对边与斜边的比叫做∠A的________,记作________,即_________.
(二)、自我检测
1、 如图(1),在Rt△ABC中,
∠C=90°,求sinA=_____ sinB=______.
2、 如图(2),在Rt△ABC中,
∠C=90°,求sinA=_____ sinB=_____
3. 在△ABC中,∠C=90°,BC=2,sinA=,则边AC的长是( )
A. B.3 C. D.
4.如图,已知点P的坐标是(a,b),则sinα等于( )
A. B. C.
(三)、知新有疑
通过自学,我又知道了:__________________________________
_______________________________________________________________
【范例精析】
1、在Rt△ABC中,∠C=900,sinA=,求sinB的值.
2、如图,Rt△ABC中,∠C=900,CD⊥AB于D点,AC=3,BC=4,求sinA、sin∠BCD的值.
【达标测评】
1、在Rt△ABC中,∠C=900,AC=5cm,BC=3cm,则sinA=______,sinB=________.
2、在Rt△ABC中,∠C=900,如果各边的长度都扩大2倍,那么锐角A的正弦值( )
A、扩大两倍 B、缩小两倍 C、没有变化 D、不能确定
3、在Rt△ABC中,∠C=900,AB=15,sinA=,则AC=_______,S△ABC=_______.
4、在Rt△ABC中,∠C=900,∠A=300,BD平分∠ABC交AC边于D点,则sin∠ABD的值为______.
5、课本 第82页 习题28.1复习巩固第1题、第2题.(只做与正弦函数有关的部分)
【小结反思】
通过本节课的探究学习,我又有了新的收获和体验。
学习感受反思:_________________________________________
28.1锐角三角函数(2)导学案
执笔: 初审 : 复审:王梅
授课人: 课型 :新授 课时:1课时
学生姓名: 班级: 小组:
【学习目标】
1、 感知当直角三角形的锐角固定时,它的邻边与斜边、对边与邻边的比值也都固定这一事实。
2、逐步培养学生观察、比较、分析、概括的思维能力。
【学习重点】理解余弦、正切的概念。
【学习难点】熟练运用锐角三角函数的概念进行有关计算。
【导引教学】
【情境导入】
1、我们是怎样定义直角三角形中一个锐角的正弦的?
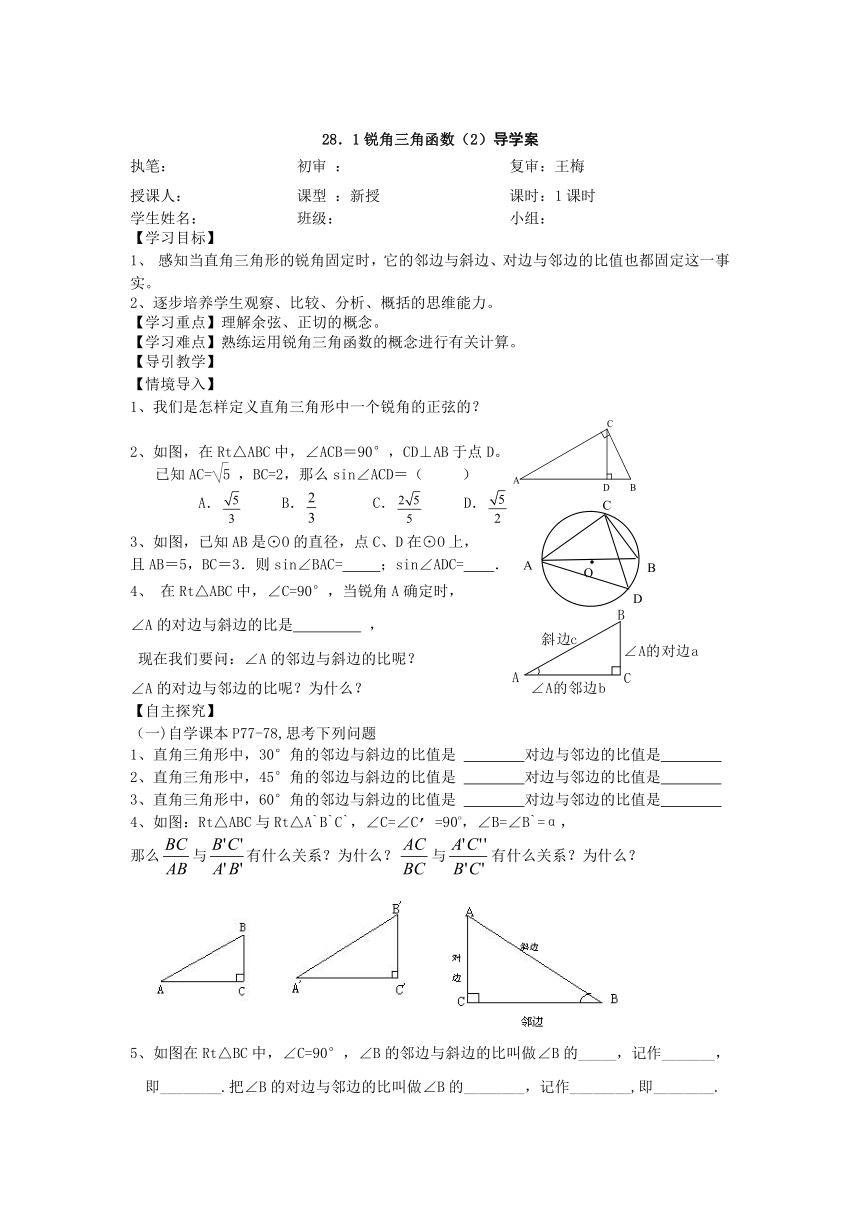
2、如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D。
已知AC=,BC=2,那么sin∠ACD=( )
A. B. C. D.
3、如图,已知AB是⊙O的直径,点C、D在⊙O上,
且AB=5,BC=3.则sin∠BAC= ;sin∠ADC= .
4、在Rt△ABC中,∠C=90°,当锐角A确定时,
∠A的对边与斜边的比是 ,
现在我们要问:∠A的邻边与斜边的比呢?
∠A的对边与邻边的比呢?为什么?
【自主探究】
(一)自学课本P77-78,思考下列问题
1、直角三角形中,30°角的邻边与斜边的比值是 对边与邻边的比值是
2、直角三角形中,45°角的邻边与斜边的比值是 对边与邻边的比值是
3、直角三角形中,60°角的邻边与斜边的比值是 对边与邻边的比值是
4、如图:Rt△ABC与Rt△A`B`C`,∠C=∠C’ =90o,∠B=∠B`=α,
那么与有什么关系?为什么?与有什么关系?为什么?
5、如图在Rt△BC中,∠C=90°,∠B的邻边与斜边的比叫做∠B的_____,记作_______,即________.把∠B的对边与邻边的比叫做∠B的________,记作________,即________.
6、锐角A的________、________、________都叫做∠A的锐角三角函数.
(二)自我检测
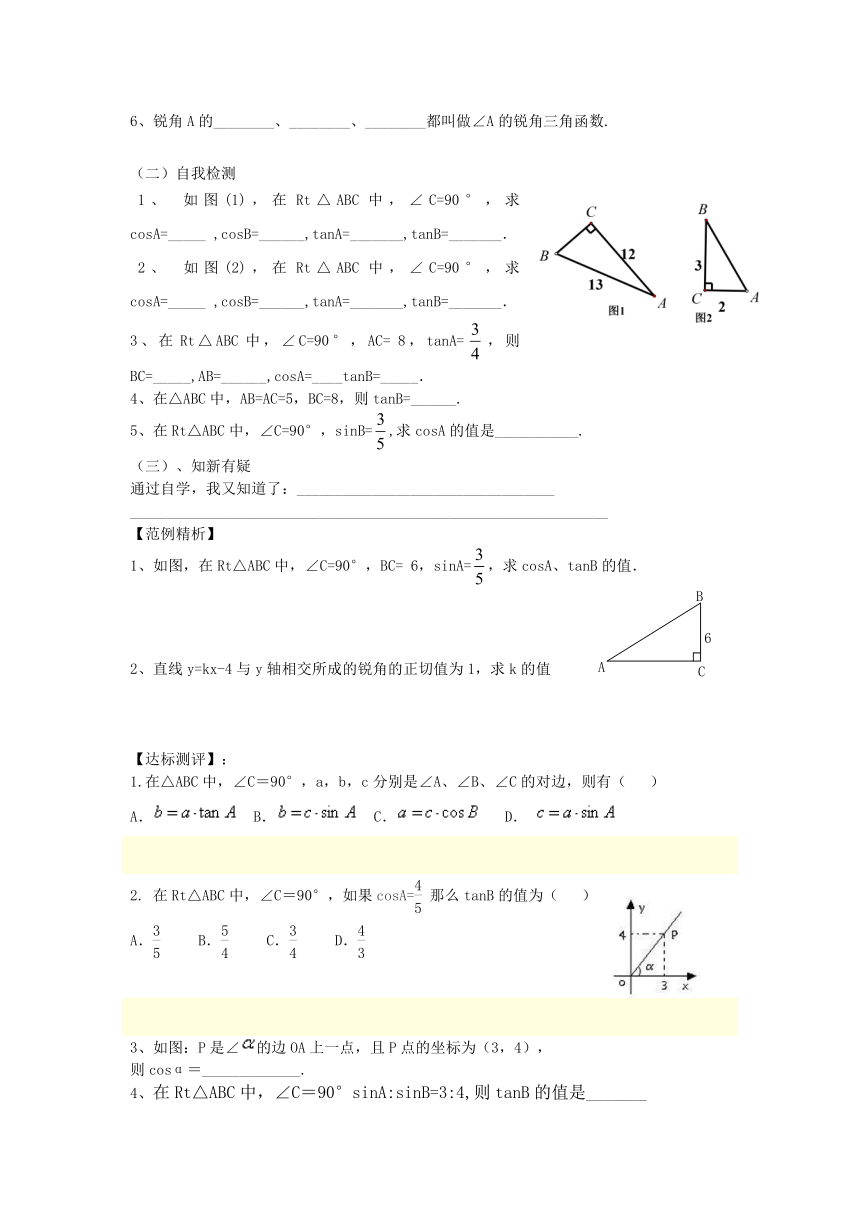
1、 如图(1),在Rt△ABC中,∠C=90°,求cosA=_____ ,cosB=______,tanA=_______,tanB=_______.
2、 如图(2),在Rt△ABC中,∠C=90°,求cosA=_____ ,cosB=______,tanA=_______,tanB=_______.
3、在Rt△ABC中,∠C=90°,AC=8,tanA=,则BC=_____,AB=______,cosA=____tanB=_____.
4、在△ABC中,AB=AC=5,BC=8,则tanB=______.
5、在Rt△ABC中,∠C=90°,sinB=,求cosA的值是___________.
(三)、知新有疑
通过自学,我又知道了:__________________________________
_______________________________________________________________
【范例精析】
1、如图,在Rt△ABC中,∠C=90°,BC=6,sinA=,求cosA、tanB的值.
2、直线y=kx-4与y轴相交所成的锐角的正切值为1,求k的值
【达标测评】:
1.在△ABC中,∠C=90°,a,b,c分别是∠A、∠B、∠C的对边,则有( )
A. B. C. D.
2. 在Rt△ABC中,∠C=90°,如果cosA=那么tanB的值为( )
A. B. C. D.
3、如图:P是∠的边OA上一点,且P点的坐标为(3,4),
则cosα=_____________.
4、在Rt△ABC中,∠C=90°sinA:sinB=3:4,则tanB的值是_______
5、在Rt△ABC中,∠C=90°,BC=5,sinA=0.7,求cosA,tanA的值.
6、课本 第82页 习题28.1复习巩固第1题、第2题.(只做与余弦、正切有关的部分)
【小结反思】
通过本节课的探究学习,我又有了新的收获和体验。
28.1锐角三角函数(3)教案
执笔: 初审 : 复审: 王梅
授课人: 课型 :新授 课时:1课时
学生姓名: 班级: 小组:
【学习目标】
1、 能推导并熟记30°、45°、60°角的三角函数值,并能根据这些值说出对应锐角度数。
2、 能熟练计算含有30°、45°、60°角的三角函数的运算式
【学习重点】熟记30°、45°、60°角的三角函数值
【学习难点】30°、45°、60°角的三角函数值的推导过程
【导引教学】
【情境导入】:
1、如图(1)在Rt△ACB中, ∠C=90°,∠A=30°,若BC=a,则AB=______,AC= _______,
∠B=____0,sinA=______,cosA=_______,tanA=_______ ,sinB=______,cosB=_______,tanB=_______
2、如图(2)在Rt△ACB中,∠C=90°,若∠A =45°,BC=m,则∠B=________AC= ________,AB=________, sinA=______,cosA=_______,tanA=_______。
【自主探究】:
思考:1、两块三角尺中有几个不同的锐角?__________, 分别是____________度?
2、你能分别求出这几个锐角的正弦值、余弦值和正切值吗?.
30°
45°
60°
siaA
cosA
tanA
3、填表
观察上表发现:(1)一个锐角的度数越大,它的正弦值_______,余弦值_______,正切值_______,
(2) sinA 、 cosA 、 tanA的取值范围分别是________________________.
(3)sin300==__________,
(二)自我检测
1、计算cos600=______ tan300=_______ 2sin450=_______ tan2450=______
2、若sinA=,则∠A=_____;若tanA=,则∠A=_____;若cosA=,则∠A=_____;
3、计算2sin30°-2cos60°+tan45°的结果是_______. 4、sin272°+sin218°的值是_________.
(三)、知新有疑 通过自学,我又知道了:____________________________________________________________。
【范例精析】:
例3:求下列各式的值.
(1)cos260°+sin260°. (2)-tan45°.
例4:(1)如图(1),在Rt△ABC中,∠C=90,AB=,BC=,求∠A的度数.
(2)如图(2),已知圆锥的高AO等于圆锥的底面半径OB的倍,求a.
【达标测评】
1.下列各式中不正确的是( ).
A.sin260°+cos260°=1 B.sin30°+cos30°=1 C.sin35°=cos55° D.tan45°>sin45°
2.已知∠A为锐角,且cosA≤,那么( )
A.0°<∠A≤60°B.60°≤∠A<90° C.0°<∠A≤30°D.30°≤∠A<90°
3.在△ABC中,∠A、∠B都是锐角,且sinA=,cosB=,则△ABC的形状是( )
A.直角三角形 B.钝角三角形C.锐角三角形 D.不能确定
4.如图Rt△ABC中,∠ACB=90°,CD⊥AB于D,BC=3,AC=4,设∠BCD=a,则tana的值为( ). A. B. C. D.
5.当锐角a>60°时,cosa的值( ).
A.小于 B.大于 C.大于 D.大于1
6.若(tanA-3)2+│2cosB-│=0,则△ABC( ).
A.是直角三角形 B.是等边三角形
C.是含有60°的任意三角形 D.是顶角为钝角的等腰三角形
7.设α、β均为锐角,且sinα-cosβ=0,则α+β=_______.
8.已知,等腰△ABC的腰长为4,底为30°,则底边上的高为______,周长为______.
9、课本P80练习1、2 P82习题3
【小结反思】
28.2解直角三角形
执笔: 王增梅 初审 :王银 复审:王富贵
授课人: 课型 :新授 课时:1课时
学生姓名: 班级: 小组:
【学习目标】
1.理解直角三角形中五个元素的关系,会运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形
2.通过综合运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形,逐步培养分析问题、解决问题的能力.
3.渗透数形结合的数学思想,培养良好的学习习惯.
【学习重点】 灵活运用知识点,准确解直角三角形
【学习难点】 三角函数在解直角三角形中的灵活运用
【自主探究】
一.导引自学,阅读书本P85-86,回答以下问题 :
解直角三角形的定义是什么?
说一说P85的探究结果。
例1中知道什么,求什么?用到了哪些关系式解决的?运用到什么数学思想方法?
例2中除了3的问题外,你还有其他方法求c吗?
二.自我检测
(一)完成课本87页练习
(二).1.在△ABC中,∠C=90°,若b=,c=2,则tanB=__________
2.在Rt△ABC中,∠C=90°,sinA=,AB=10,则BC=______.
3.在△ABC中,∠C=90°,若a:b=5:12则sinA= .
4. 在直角三角形ABC中,∠C=90°,∠A=30°,斜边上的高h=1,则三边的长分别是_____________________.
5.如图,在Rt△ABC中,∠C=90°,tanA=, COSB=___________.
6. 如图,在Rt△ABC中,∠C=90°,AB=6,AD=2,则sinA=____;tanB=____.
4、如图在△ABC中,∠C=900,∠A=300.D为AC上一点,AD=10,∠BDC=600,求AB的长
三.知新有疑:__________________________________________________________________
【范例精析】在△ABC中,∠C=900点D在C上,BD=4,AD=BC,cos∠ADC=,求(1)DC的长;(2)sinB的值;
【达标测评】
1.根据直角三角形的__________元素(至少有一个边),求出________其它所有元素的过程,即解直角三角形.
2、Rt△ABC中,若sinA=,AB=10,那么BC=_____,tanB=______.
3、在△ABC中,∠C=90°,AC=6,BC=8,那么sinA=________.
4、在△ABC中,∠C=90°,sinA= 则cosA的值是
5、在Rt△ABC中,∠C=90°,a=,b=3,解这个三角形.
6、?在△ABC中,∠C为直角,AC=6,的平分线AD=4,解此直角三角形。
7. 书本92页习题1
【课堂小结】
28.2 解直角三角形的应用(1)----仰角、俯角导学案
执笔: 王增梅 初审 :王银 复审:王富贵
授课人: 课型 :新授 课时:1课时
学生姓名: 班级: 小组:
【学习目标】
1: 使学生了解仰角、俯角的概念,使学生根据直角三角形的知识解决实际问题.
2: 逐步培养学生分析问题、解决问题的能力.
3: 渗透数学来源于实践又反过来作用于实践的观点,培养学生用数学的意识
【学习重点】 将某些实际问题中的数量关系,归结为直角三角形元素之间的关系,从而利用所学知识把实际问题解决.
【学习难点】 实际问题转化成数学模型
【自主探究】
一、导引自学:阅读书本P87-88,思考以下问题
1.例1中 根据哪个知识来找地球的最远点?可将问题到一个什么几何图形中解决?根据示意图,用什么知识解出来的?你知道每一步的依据吗?体现了数学中的哪些思想方法?
2.(1)例2中你知道什么叫仰角俯角吗?画出图形 。
(2)如何把实际问题转化成几何问题?可将问题到一个什么几何图形中解决?根据示意图,用什么知识解出来的?你知道每一步的依据吗?体现了数学中的哪些思想方法?
二.自我检测书本89页练习1.2
3.知新有疑
【范例精析】:
在山脚C处测得山顶A的仰角为45°。问题如下:
1.沿着水平地面向前300米到达D点,在D点测得山顶A的仰角为60 °,求山高AB。
2.沿着坡角为30 °的斜坡前进300米到达D点,在D点测得山顶A的仰角为60 ° ,求山高AB。
【达标测评】:
1、直升飞机在高为200米的大楼AB上方P点处,从大楼的顶部和底部测得飞机的仰角为30°和45°,求飞机的高度PO .
2、如图所示,小杨在广场上的A处正面观测一座楼房墙上的广告屏幕,测得屏幕下端D处的仰角为30o,然后他正对大楼方向前进5m到达B处,又测得该屏幕上端C处的仰角为45o.若该楼高为26.65m,小杨的眼睛离地面1.65m,广告屏幕的上端与楼房的顶端平齐.求广告屏幕上端与下端之间的距离(≈1.732,结果精确到0.1m).
3.某旅游区有一个景观奇异的望天洞,点是洞的入口,游人从入口进洞游览后,可经山洞到达山顶的出口凉亭处观看旅游区风景,最后坐缆车沿索道返回山脚下的处.在同一平面内,若测得斜坡的长为100米,坡角,在处测得的仰角,在处测得的仰角,过点作地面的垂线,垂足为.
(1)求的度数;
(2)求索道的长.(结果保留根号)
4.书本92-93页3.4.7
【小结反思】
28.2 解直角三角形的应用(2)----方位角教学案
执笔: 王梅 初审 :王银 复审:王富贵
授课人: 课型 :新授 课时:1课时
学生姓名: 班级: 小组:
【教学目标】
1.使学生理解方位角概念的意义,并能适当的选择锐角三角函数关系式去解决有关直角三角形实际问题;
2. 培养学生将实际问题抽象为数学问题(画出平面图形?转化为解直角三角形)的能力
【教学重点】用三角函数有关知识解决方位角的实际问题
【教学难点】学会准确分析问题并将实际问题转化成数学模型
【自主探究】
一. 导引自学:阅读书本P89例5,思考以下问题
1.(1)方位角的定义是什么?
(2)画出以下方位角;南偏东300 ; 南偏西600;北偏西150 ; 东北方向。
(3)A点在B点的南偏东360,,则B点在A点的什么方向?
2.例2中如何把实际问题转化成几何问题?可将问题到一个什么几何图形中解决?根据示意图,用什么知识解出来的?你知道每一步的依据吗?体现了数学中的哪些思想方法?
3.你知道利用直角三角形的知识解决实际问题的一般步骤吗?
二.自我检测:
1.如图,太阳光线与地面成60°角,一棵倾斜的大树与地面成30°角,这时测得大树在地面上的影子约为10米,则大树的高约为________米.(结果保留根号)
2. 王英同学从A地沿北偏西60o方向走100m到B地,再从B地向正南方向走200m到C地,此时王英同学离A地 ( )
A.150m B.m C.100 m D.m
3.如图所示,海上有一灯塔P,在它周围3海里处有暗礁.一艘客轮以9海里/时?的速度由西向东航行,行至A点处测得P在它的北偏东60°的方向,继续行驶20分钟后,到达B处又测得灯塔P在它的北偏东45°方向.问客轮不改变方向继续前进有无触礁的危险?
4.书本91页练习1
三.知新有疑
【范例精析】
如图,某货船以20海里/时的速度将一批重要物资由A处运往正西方向的B处,经16小时的航行到达,到达后必须立即卸货.此时.接到气象部门通知,一台风中心正以40海里/时的速度由A向北偏西60°方向移动,距台风中心200海里的圆形区域(包括边界)均受到影响.
(1)B处是否会受到台风的影响?请说明理由.
(2)为避免受到台风的影响,该船应在多少小时内卸完货物?(供选用数据:≈1.4, ≈1.7)
【达标测评】
1.上午10点整,一渔轮在小岛O的北偏东30°方向,距离等于10海里的A处,正以每小时10海里的速度向南偏东60°方向航行.那么渔轮到达小岛O的正东方向是什么时间?(精确到1分).
2、在东西方向的海岸线上有一长为1km的码头MN(如图),在码头西端M 的正西19.5 km 处有一观察站A.某时刻测得一艘匀速直线航行的轮船位于 A 的北偏西30°,且与A相距40km的B处;经过1小时20分钟,又测得该轮船位于A的北偏东60°,且与A相距km的C处.
(1)求该轮船航行的速度(保留精确结果);
(2)如果该轮船不改变航向继续航行,那么轮船能否正
好行至码头MN靠岸?请说明理由.
3.书本93页习题9
【自我反思】
1、知识技能: 。
2、思想方法: 。
28.2解直三角形应用(三)----坡度问题
执笔: 王梅 初审 :王增梅 复审:王富贵
授课人: 课型 :新授 课时:1课时
学生姓名: 班级: 小组:
【教学目标】
1.巩固用三角函数有关知识解决问题,学会解决坡度问题.
2.逐步培养学生分析问题、解决问题的能力;渗透数形结合的数学思想和方法.
3.培养学生用数学的意识,渗透理论联系实际的观点.
【教学重点】:解决有关坡度的实际问题.
【教学难点】:理解坡度的有关术语.
【自主探究】
一.导引自学:自学书本p90-91思考以下问题
1.坡面的铅直高度h和水平宽度的比叫做坡度(或叫做坡比),
2.一般用i表示。即i=( )常写成i=1:m的形式如i=1:2.5把坡面与水平面的夹角α叫做坡角.
3.结合图形思考,坡度i与坡角α之间具有什么关系?
二.自我检测:
1.一段坡面的坡角为60°,则坡度i=______;
______,坡角______度.
2.书本91页练习2
3.如图,一水坝横断面为等腰梯形ABCD,斜坡AB的坡度为1∶,坡面AB的水平宽度为3米,上底宽AD为4米,求坡角B,坝高AE和坝底宽BC各是多少?
三.知新有疑
【范例精析】
某海港区为提高某段海堤的防海潮能力,计划将100米的一段堤(原海堤的横断面如图中的梯形ABCD)的堤面加宽1米,背水坡度由原来的1:1改成1:2。已知原背水坡长AD= 米,求完成这一工程所需的土方数。
【达标测评】
1、如图,沿江堤坝的横断面是梯形ABCD,坝顶AD=4m,坝高AE=6 m,斜坡AB的坡比,∠C=60°,求斜坡AB、CD的长。
2、同学们,如果你是修建三峡大坝的工程师,现在有这样一个问题请你解决:如图水库大坝的横断面是梯形,坝顶宽6m,坝高23m,斜坡AB的坡度i=1∶3,斜坡CD的坡度i=1∶2.5,求斜坡AB的坡面角α,坝底宽AD和斜坡AB的长(精确到0.1m)
3.书本92-93习题5.6.8
.
【课堂小结】:
1.把实际问题转化成数学问题,转化包括两个方面:一是(将实际问题的图形转化为几何图形,画出正确的示意图);二是(将已知条件转化为示意图中的边、角或它们之间的关系).
2.把数学问题转化成解直角三角形问题,如果示意图不是直角三角形,可(添加适当的辅助线),画出(直角)三角形.
数学活动——利用测角仪测量物体的高度导学案
执笔: 谢力 初审 :王银 复审:王富贵
授课人:谢力 课型 :新授 课时:1课时
学生姓名: 班级: 小组:
【学习目标】
1、通过测量和计算大树、塔高度的活动,巩固三角函数的有关知识。
并在活动中积累数学活动经验。
2、通过测量活动,使我初步学会数学建模的方法.,提高综合运用知识的能力.
【教学重点】掌握利用测角仪测量物体的高度的操作方法,并能运用三角函数的知识解决实际问题。
【教学难点】学会如何在实际问题中构造直角三角形,建立三角函数的模型和图形模型。
【自主探究】
一、导引自学:自学课本98——99页完成下列问题
1、右图中仪器的名称是 ,它是用来 。
2、用手中的量角器制作一个1题中的测量工具。
3、测量活动:
活动一:利用制作的测量工具测量大树的高度。
请你设计一个测量方案,亲自测量后,回答下列问题:
(1)在你设计的方案中,选用的测量工具有
(2)你需要用 测得你到树根的距离是 ,用 测量你看到的树的顶端的仰角是 ,还需要知道 。
(3)在右图中画出你的测量方案示意图;
(4)写出求树高的算式:AB=
活动二:利用制作的测量工具测量塔的高度。
请设计出实际操作方案,并根据方案回答问题:
(1)在你设计的方案中,选用的测量工具是
(用工具的序号填写)
(2)在右图中画出你的测量方案示意图;
(3)你需要测得示意图中的哪些数据,并分别用a、b、c、α等表示测得的数据:
(4)写出求塔高的算式:
问题:活动一与活动二的方法有何优、缺点?还有别的测量方法吗?
二、自我检测:
如图,小明欲利用测角仪测量树的高度.已知他离树的水平距离BC为10m,测角仪的高度CD为1.5m,测得树顶A的仰角为33°.求树的高度AB.(参考数据:sin33°≈0.54,cos33°≈0.84,tan33°≈0.65)
三、知新有疑 :通过自学
我的收获是:
我的疑惑是:
【范例精析】
蒿坪中学九年级的李明同学想知道学校旗杆的高度,但手中只有刚制作的测角仪,在下列情形下他能测出旗杆的高度吗?(测出的角用α、β表示)
(1)他站在距旗杆15米的教学楼三楼上,却不知三层楼的高度,此时他是怎样测量旗杆的高度呢?
(2)他站在距旗杆15米远,且高为24米的教学楼楼顶上,他又是怎么测出的呢?
(3)这次他站在离建筑物15米的地面上测,可是建筑物将旗杆的一部分挡住了,已知李明同学的身高是1.6米,你知道他是怎么测得吗?
【达标测评】
1、小明利用所学的数学知识测量生活中一建筑物的高AB.(1)请帮小明写出具体的测量方法?并画图表示(角用1、2、3表示,线段用a、b、c表示)(2)请用你测得的数据帮助小明求出建筑物AB的高.
【小结反思】
学生自由发言,总结学习收获体验;
解直角三角形复习(1)
执笔:王银 初审:王梅 复审:王富贵
授课人: 课型:复习课 课时:1
学生姓名: 班级: 小组:
【教学目标】:通过复习,使学生系统地掌握本章知识。在系统复习知识的同时,使学生能够灵活运用知识解决问题。
【教学重点】:通过复习,使学生系统地掌握本章知识。
【教学难点】: 在系统复习知识的同时,使学生能够灵活运用知识解决问题。
一、自主探究
1.本章学习了哪些知识,用到了哪些数学思想方法?
2.自己尝试画出知识结构图
【范例精析】:
例1.Rt△ABC中,∠C=90°,∠B=60°,两直角边的和为14,求这个直角三角形的面积。
例2.如图,AC⊥BC,cos∠ADC=,∠B=30°AD=10,求 BD的长。
例3.Rt△ABC中,∠C=90°,AC=8,∠A的平分线AD=,求∠B的度数以及边BC、AB的长。
【当堂检测】.
一、选择题
1、如图,点P(3,4)是∠α的边OA上的一点,则Sinα= .
A、 B、 C、 D、
2、某市为改善交通状况,修建了大量的高架桥,一汽车在坡度为300的笔直高架桥点A开始爬行,行驶了150米到达B点,这时汽车离地面高度为 米.
A、300 B、150 C、75 D、50
3、把Rt△ABC的各边都扩大3倍得Rt△A/B/C/,那么锐角A、A/ 的余弦值的关系是 .
A、cosA = cosA/ B、cosA = 3cosA/
C、3cosA = cosA/ D、不能确定
4、已知锐角A的cosA≤,则锐角A的取值范围是 .
A、0<A≤600 B、600≤A<900 C、0<A≤300 D、300≤A<900
5、王英从A地向北偏西600方向走100米到B地,再从B地向正南方向走200米到C地,此时王英离A地有 米.
A、50 B、100 C、150 D、100
6、在Rt△ABC中,∠C = 900,tanA = ,则SinB = .
A、 B、 C、 D、
7、在Rt△ABC中,∠C = 900,CD是斜边AB上的中线,CD = 2,AC = 3,则 SinB = .
A、 B、 C、 D、
8.Rt△ABC中,∠C=90°,∠A=30°,∠A、∠B、∠C所对的边为a、b、c,则a:b:c=( )
A、1:2:3 B、1: : C、1: :2 D、1:2:
9.下列说法正确的是( )
A.在△ ABC中,若∠A的对边是3,一条邻边是5,则tanA=
B.将一个三角形的各边扩大3倍,则其中一个角的正弦值也扩大3倍
C.在锐角△ ABC中,已知∠A=60°,那么cosA=
D.一定存在一个锐角A,使得sinA=1.23
10.已知锐角α,且sinα=cos37°,则a等于( )
A.37° B.63° C.53° D.45°
11.当锐角α>30°时,则cosα的值是( )
A.大于 B.小于 C.大于 D.小于
12.求值:
(1) 6tan2 30°-sin 60°+2tan45°
(2)
解直角三角形复习(2)
执笔:王银 初审:王梅 复审:王富贵
授课人: 课型:复习课 课时:1
学生姓名: 班级: 小组:
【教学目标】:
使学生掌握直角三角形的边与边,角与角,边与角的关系,能应用这些关系解决相关的问题,进一步培养学生应用知识解决问题的能力。
【教学重点】:学生掌握直角三角形的边与边,角与角,边与角的关系
【教学难点】:能应用这些关系解决相关的实际问题,进一步培养学生应用知识解决问题的能力。
【自主探究】
1.说一说直角三角形中边角有哪些关系?
2. 说一说仰角.俯角.方位角.坡角的定义,画图说明.
3. 你知道利用直角三角形的知识解决实际问题的一般步骤吗?
【自我检测】
1.甲、乙、丙三个梯子斜靠在一堵墙上(梯子顶端靠墙), 小明测得:甲与地面的夹角为60°;乙的底端距离墙脚米,且顶端距离墙脚3米;丙的坡度为。那么,这三张梯子的倾斜程度( )
A.甲较陡 B.乙较陡 C.丙较陡 D.一样陡
2、小琳家在门前O处,有一条东西走向的公路,经测得有一水塔A在她家北偏东
600的500米处,那么水塔所在的位置到公路的距离AB = 米.
A、250 B、250 C、 D、250
3.如图,沿AC方向开山修路,为了加快施工进度,要在山的另一边同时施工,现在从AC上取一点B,使得∠ABD=145°,BD=500米,∠D=55°,要使A、C、E在一条直线上,那么开挖点E离点D的距离是( )
A.500sin55°米 B.500cos55°米
C.500tan55°米; D.米
4、如图,轮船由南向北航行到O处,发现与轮船相距40海里的A岛在北偏东330方向上的A岛周围20海里水域内有暗礁,若不改变航向,则轮船 触礁的危险.(有或无)
5.若A在B的北偏东20°处,那么B在A的 方向上.
6.某山路的路面坡度ⅰ=1:,沿此山路向前走200米,则人升高了___ __米.
7.每周一学校都要举行庄严的升国旗仪式,让我们感受到了国旗的神圣.升国旗时,某同学站在离旗杆底部24米处行注目礼,当国旗升至旗杆顶端时,该同学视线的仰角恰为30°,若双眼离地面1.5米,则旗杆的高度为__ ____米。(用含根号的式子表示)
【范例精析】 例1.北部湾海面上,一艘解放军军舰正在基地A的正东方向且距离A地40海里的B处训练。突然接到基地命令,要该舰前往C岛,接送一名病危的渔民到基地医院救治。已知C岛在A的北偏东方向60°,且在B的北偏西45°方向,军舰从B处出发,平均每小时行驶20海里,需要多少时间才能把患病渔民送到基地医院?(精确到0.1小时)
例3.如图5,某防洪指挥部发现长江边一处长500米,高I0米,背水坡的坡角为45°的防洪大堤(横断面为梯形ABCD)急需加固.经调查论证,防洪指挥部专家组制定的加固方案是:沿背水坡面用土石进行加固。并使上底加宽3米,加固后背水坡EF的坡比i=1:。
(I)求加固后坝底增加的宽度AF;
(2)求完成这项工程需要土石多少立方米?(结果保留根号)
【当堂检测】:
1.如图,城市规划期间,欲拆除一电线杆AB,已知电线杆AB距水平距离14m的D处有有大坝,背水坡CD的坡度,坝高C F为2m,在坝顶C处测地杆顶的仰角为,D、E之间是宽度位2m的人行道。试问:在拆除电线杆AB时,为确保行人安全是否需要将此人行道封闭?请说明你的理由(在地面上以B为圆心,以AB为半径的图形区域为危险区域,)。
2、在某建筑物AC上挂着“多彩贵州” 的宣传条幅BC,小明站在点F处,看条幅顶端B,测得仰角为300,再往条幅方向前行20米到达点E处,看到条幅顶端B,测得仰角为600,求宣传条幅BC的长. (小明的身高不计,结果精确到O.1米)
第28章锐角三角函数单元测试卷
一、选择(每题 3分,合计 30分 )
1. 在,,,则等于( )
A. B. C. D.1
2. 在Rt△ABC中 ,,,则的值是( )
A. B. C. D.
3. 中,,且,则等于( )
A. B. C. D.
4. 等腰三角形的边长为6,8,则底角的余弦是( )
A. B. C. D.和
5. 某市在旧城改造中,计划在市内一块如图1所示三角形空地上种植草皮以美化环境,已知这种草皮每平方米售价元,则购买这种草皮至少需要( )
A.450元 B.元
C.元 D.元
6.如图2,一个钢球沿坡角的斜坡向上滚动了米,此时钢球距地面的高度是( )米.
A. B. C. D.
7. 若,则以∠A、∠B为内角的一定是( ).
A.等腰三角形 B.等边三角形 C.直角三角形 D.锐角三角形
8. .如图3,在中,,于,若,
,则的值为( ).
A. B. C. D.
9. 如图4,有两条宽度为1的带子,相交成角,那么重叠部分(阴影)
的面积是( ).
A.1 B. C. D.
10. 如图5,在高楼前点测得楼顶的仰角为,向高楼前
进60米到点,又测得仰角为,则该高楼的高度大
约为( ).
A.82米 B.163米 C.52米 D.70米
二、填空(每题3分,合计21分)
1. 在△ABC中,若∠A=30°,∠B=45°,AC=,则BC=
2. .在中,,,则
3. 离旗杆20米处的地方用测角仪测得旗杆顶的仰角为, 如果测角仪高为1.5米.那么旗杆的高 为米(用含的三角函数表示)。
4. 在正方形网格中,的位置如图6所示,则的值为______.
5. 如图7,在坡度为的山坡上种树,要求株距(相邻两树间的水平距离)是6米,斜坡上相邻两树间的坡面距离是 米
6. 如图8,已知正方形的边长为3,如果将线段绕点旋转后,点落在延长线上的点处,那么 .
7. 如图9,钓鱼竿长,露在水面上的鱼线长,某钓者想看看鱼钓上的情况,把鱼竿转动到的位置,此时露在水面上的鱼线为,则鱼竿转过的角度是________.
三、解答题
1. 计算求值:(每题5分,合计20分)
(1); (2);
(3); (4)
2. 如图10,在平地处测得树顶的仰角为,向树前进10m,到达处,再测得树顶的仰角为,求树高(结果保留根号).(9分)
3. 如图11,某边防巡逻队在一个海滨浴场岸边的A点处发现海中的B点有人求救,便立即派三名救生员前去营救.1号救生员从A点直接跳入海中;2号救生员沿岸边(岸边看成是直线)向前跑到C点,再跳入海中;3号救生员沿岸边向前跑3 0 0米到离B点最近的D点,再跳人海中.救生员在岸上跑的速度都是6米/秒,在水中游泳的速度都是2米/秒.若,,三名救生员同时从A点出发,请说明谁先到达营救地点B. (参考数据≈1.4,≈1.7) (10分)
4. 如图12所示,某超市在一楼至二楼之间安装有电梯,天花板与地面平行,请你根据图中数据计算回答:
小敏身高1.78米,她乘电梯会有碰头危险吗?姚明身高2.29米,他乘电梯会有碰头危险吗?
(可能用到的参考数值:,,)(10分)
执笔: 初审 : 复审: 王梅
授课人: 课型 :新授 课时:1课时
学生姓名: 班级: 小组:
【教学目标】
初步了解锐角三角函数的意义,初步理解在直角三角形中一个锐角的对边与斜边的比值就是这个锐角的正弦的定义。.
2、会根据已知直角三角形的边长求一个锐角的正弦值。
【教学重点】锐角的正弦的定义。
【教学难点】理解直角三角形中一个锐角与其对边及斜边比值的对应关系。
【导引教学】
【情境导入】
1、如图在Rt△ABC中,∠C=90°,∠A=30°,BC=10m,求AB
2、如图在Rt△ABC中,∠C=90°,∠A=30°,AB=20m,求BC
【自主探究 】
(一)、自学课本P74-76 思考下列问题:
思考1:如果使出水口的高度为50m,那么需要准备多长的水管? ;
如果使出水口的高度为a m,那么需要准备多长的水管? ;
结论:直角三角形中,30°角的对边与斜边的比值是
思考2:在Rt△ABC中,∠C=90°,∠A=45°,∠A对边与斜边
的比值是一个定值吗?如果是,是多少?
结论:直角三角形中,45°角的对边与斜边的比值
思考3:在Rt△ABC中,∠C=90°,∠B=60°,∠B对边与斜边
的比值是一个定值吗?如果是,是多少?
结论:直角三角形中,60°角的对边与斜边的比值
思考4: Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,
∠A=∠A′=a,那么有什么关系.为什么?
结论:这就是说,在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与斜边的比值
5、在Rt△ABC中,∠C=90°,我们把锐角A的对边与斜边的比叫做∠A的________,记作________,即_________.
(二)、自我检测
1、 如图(1),在Rt△ABC中,
∠C=90°,求sinA=_____ sinB=______.
2、 如图(2),在Rt△ABC中,
∠C=90°,求sinA=_____ sinB=_____
3. 在△ABC中,∠C=90°,BC=2,sinA=,则边AC的长是( )
A. B.3 C. D.
4.如图,已知点P的坐标是(a,b),则sinα等于( )
A. B. C.
(三)、知新有疑
通过自学,我又知道了:__________________________________
_______________________________________________________________
【范例精析】
1、在Rt△ABC中,∠C=900,sinA=,求sinB的值.
2、如图,Rt△ABC中,∠C=900,CD⊥AB于D点,AC=3,BC=4,求sinA、sin∠BCD的值.
【达标测评】
1、在Rt△ABC中,∠C=900,AC=5cm,BC=3cm,则sinA=______,sinB=________.
2、在Rt△ABC中,∠C=900,如果各边的长度都扩大2倍,那么锐角A的正弦值( )
A、扩大两倍 B、缩小两倍 C、没有变化 D、不能确定
3、在Rt△ABC中,∠C=900,AB=15,sinA=,则AC=_______,S△ABC=_______.
4、在Rt△ABC中,∠C=900,∠A=300,BD平分∠ABC交AC边于D点,则sin∠ABD的值为______.
5、课本 第82页 习题28.1复习巩固第1题、第2题.(只做与正弦函数有关的部分)
【小结反思】
通过本节课的探究学习,我又有了新的收获和体验。
学习感受反思:_________________________________________
28.1锐角三角函数(2)导学案
执笔: 初审 : 复审:王梅
授课人: 课型 :新授 课时:1课时
学生姓名: 班级: 小组:
【学习目标】
1、 感知当直角三角形的锐角固定时,它的邻边与斜边、对边与邻边的比值也都固定这一事实。
2、逐步培养学生观察、比较、分析、概括的思维能力。
【学习重点】理解余弦、正切的概念。
【学习难点】熟练运用锐角三角函数的概念进行有关计算。
【导引教学】
【情境导入】
1、我们是怎样定义直角三角形中一个锐角的正弦的?
2、如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D。
已知AC=,BC=2,那么sin∠ACD=( )
A. B. C. D.
3、如图,已知AB是⊙O的直径,点C、D在⊙O上,
且AB=5,BC=3.则sin∠BAC= ;sin∠ADC= .
4、在Rt△ABC中,∠C=90°,当锐角A确定时,
∠A的对边与斜边的比是 ,
现在我们要问:∠A的邻边与斜边的比呢?
∠A的对边与邻边的比呢?为什么?
【自主探究】
(一)自学课本P77-78,思考下列问题
1、直角三角形中,30°角的邻边与斜边的比值是 对边与邻边的比值是
2、直角三角形中,45°角的邻边与斜边的比值是 对边与邻边的比值是
3、直角三角形中,60°角的邻边与斜边的比值是 对边与邻边的比值是
4、如图:Rt△ABC与Rt△A`B`C`,∠C=∠C’ =90o,∠B=∠B`=α,
那么与有什么关系?为什么?与有什么关系?为什么?
5、如图在Rt△BC中,∠C=90°,∠B的邻边与斜边的比叫做∠B的_____,记作_______,即________.把∠B的对边与邻边的比叫做∠B的________,记作________,即________.
6、锐角A的________、________、________都叫做∠A的锐角三角函数.
(二)自我检测
1、 如图(1),在Rt△ABC中,∠C=90°,求cosA=_____ ,cosB=______,tanA=_______,tanB=_______.
2、 如图(2),在Rt△ABC中,∠C=90°,求cosA=_____ ,cosB=______,tanA=_______,tanB=_______.
3、在Rt△ABC中,∠C=90°,AC=8,tanA=,则BC=_____,AB=______,cosA=____tanB=_____.
4、在△ABC中,AB=AC=5,BC=8,则tanB=______.
5、在Rt△ABC中,∠C=90°,sinB=,求cosA的值是___________.
(三)、知新有疑
通过自学,我又知道了:__________________________________
_______________________________________________________________
【范例精析】
1、如图,在Rt△ABC中,∠C=90°,BC=6,sinA=,求cosA、tanB的值.
2、直线y=kx-4与y轴相交所成的锐角的正切值为1,求k的值
【达标测评】:
1.在△ABC中,∠C=90°,a,b,c分别是∠A、∠B、∠C的对边,则有( )
A. B. C. D.
2. 在Rt△ABC中,∠C=90°,如果cosA=那么tanB的值为( )
A. B. C. D.
3、如图:P是∠的边OA上一点,且P点的坐标为(3,4),
则cosα=_____________.
4、在Rt△ABC中,∠C=90°sinA:sinB=3:4,则tanB的值是_______
5、在Rt△ABC中,∠C=90°,BC=5,sinA=0.7,求cosA,tanA的值.
6、课本 第82页 习题28.1复习巩固第1题、第2题.(只做与余弦、正切有关的部分)
【小结反思】
通过本节课的探究学习,我又有了新的收获和体验。
28.1锐角三角函数(3)教案
执笔: 初审 : 复审: 王梅
授课人: 课型 :新授 课时:1课时
学生姓名: 班级: 小组:
【学习目标】
1、 能推导并熟记30°、45°、60°角的三角函数值,并能根据这些值说出对应锐角度数。
2、 能熟练计算含有30°、45°、60°角的三角函数的运算式
【学习重点】熟记30°、45°、60°角的三角函数值
【学习难点】30°、45°、60°角的三角函数值的推导过程
【导引教学】
【情境导入】:
1、如图(1)在Rt△ACB中, ∠C=90°,∠A=30°,若BC=a,则AB=______,AC= _______,
∠B=____0,sinA=______,cosA=_______,tanA=_______ ,sinB=______,cosB=_______,tanB=_______
2、如图(2)在Rt△ACB中,∠C=90°,若∠A =45°,BC=m,则∠B=________AC= ________,AB=________, sinA=______,cosA=_______,tanA=_______。
【自主探究】:
思考:1、两块三角尺中有几个不同的锐角?__________, 分别是____________度?
2、你能分别求出这几个锐角的正弦值、余弦值和正切值吗?.
30°
45°
60°
siaA
cosA
tanA
3、填表
观察上表发现:(1)一个锐角的度数越大,它的正弦值_______,余弦值_______,正切值_______,
(2) sinA 、 cosA 、 tanA的取值范围分别是________________________.
(3)sin300==__________,
(二)自我检测
1、计算cos600=______ tan300=_______ 2sin450=_______ tan2450=______
2、若sinA=,则∠A=_____;若tanA=,则∠A=_____;若cosA=,则∠A=_____;
3、计算2sin30°-2cos60°+tan45°的结果是_______. 4、sin272°+sin218°的值是_________.
(三)、知新有疑 通过自学,我又知道了:____________________________________________________________。
【范例精析】:
例3:求下列各式的值.
(1)cos260°+sin260°. (2)-tan45°.
例4:(1)如图(1),在Rt△ABC中,∠C=90,AB=,BC=,求∠A的度数.
(2)如图(2),已知圆锥的高AO等于圆锥的底面半径OB的倍,求a.
【达标测评】
1.下列各式中不正确的是( ).
A.sin260°+cos260°=1 B.sin30°+cos30°=1 C.sin35°=cos55° D.tan45°>sin45°
2.已知∠A为锐角,且cosA≤,那么( )
A.0°<∠A≤60°B.60°≤∠A<90° C.0°<∠A≤30°D.30°≤∠A<90°
3.在△ABC中,∠A、∠B都是锐角,且sinA=,cosB=,则△ABC的形状是( )
A.直角三角形 B.钝角三角形C.锐角三角形 D.不能确定
4.如图Rt△ABC中,∠ACB=90°,CD⊥AB于D,BC=3,AC=4,设∠BCD=a,则tana的值为( ). A. B. C. D.
5.当锐角a>60°时,cosa的值( ).
A.小于 B.大于 C.大于 D.大于1
6.若(tanA-3)2+│2cosB-│=0,则△ABC( ).
A.是直角三角形 B.是等边三角形
C.是含有60°的任意三角形 D.是顶角为钝角的等腰三角形
7.设α、β均为锐角,且sinα-cosβ=0,则α+β=_______.
8.已知,等腰△ABC的腰长为4,底为30°,则底边上的高为______,周长为______.
9、课本P80练习1、2 P82习题3
【小结反思】
28.2解直角三角形
执笔: 王增梅 初审 :王银 复审:王富贵
授课人: 课型 :新授 课时:1课时
学生姓名: 班级: 小组:
【学习目标】
1.理解直角三角形中五个元素的关系,会运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形
2.通过综合运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形,逐步培养分析问题、解决问题的能力.
3.渗透数形结合的数学思想,培养良好的学习习惯.
【学习重点】 灵活运用知识点,准确解直角三角形
【学习难点】 三角函数在解直角三角形中的灵活运用
【自主探究】
一.导引自学,阅读书本P85-86,回答以下问题 :
解直角三角形的定义是什么?
说一说P85的探究结果。
例1中知道什么,求什么?用到了哪些关系式解决的?运用到什么数学思想方法?
例2中除了3的问题外,你还有其他方法求c吗?
二.自我检测
(一)完成课本87页练习
(二).1.在△ABC中,∠C=90°,若b=,c=2,则tanB=__________
2.在Rt△ABC中,∠C=90°,sinA=,AB=10,则BC=______.
3.在△ABC中,∠C=90°,若a:b=5:12则sinA= .
4. 在直角三角形ABC中,∠C=90°,∠A=30°,斜边上的高h=1,则三边的长分别是_____________________.
5.如图,在Rt△ABC中,∠C=90°,tanA=, COSB=___________.
6. 如图,在Rt△ABC中,∠C=90°,AB=6,AD=2,则sinA=____;tanB=____.
4、如图在△ABC中,∠C=900,∠A=300.D为AC上一点,AD=10,∠BDC=600,求AB的长
三.知新有疑:__________________________________________________________________
【范例精析】在△ABC中,∠C=900点D在C上,BD=4,AD=BC,cos∠ADC=,求(1)DC的长;(2)sinB的值;
【达标测评】
1.根据直角三角形的__________元素(至少有一个边),求出________其它所有元素的过程,即解直角三角形.
2、Rt△ABC中,若sinA=,AB=10,那么BC=_____,tanB=______.
3、在△ABC中,∠C=90°,AC=6,BC=8,那么sinA=________.
4、在△ABC中,∠C=90°,sinA= 则cosA的值是
5、在Rt△ABC中,∠C=90°,a=,b=3,解这个三角形.
6、?在△ABC中,∠C为直角,AC=6,的平分线AD=4,解此直角三角形。
7. 书本92页习题1
【课堂小结】
28.2 解直角三角形的应用(1)----仰角、俯角导学案
执笔: 王增梅 初审 :王银 复审:王富贵
授课人: 课型 :新授 课时:1课时
学生姓名: 班级: 小组:
【学习目标】
1: 使学生了解仰角、俯角的概念,使学生根据直角三角形的知识解决实际问题.
2: 逐步培养学生分析问题、解决问题的能力.
3: 渗透数学来源于实践又反过来作用于实践的观点,培养学生用数学的意识
【学习重点】 将某些实际问题中的数量关系,归结为直角三角形元素之间的关系,从而利用所学知识把实际问题解决.
【学习难点】 实际问题转化成数学模型
【自主探究】
一、导引自学:阅读书本P87-88,思考以下问题
1.例1中 根据哪个知识来找地球的最远点?可将问题到一个什么几何图形中解决?根据示意图,用什么知识解出来的?你知道每一步的依据吗?体现了数学中的哪些思想方法?
2.(1)例2中你知道什么叫仰角俯角吗?画出图形 。
(2)如何把实际问题转化成几何问题?可将问题到一个什么几何图形中解决?根据示意图,用什么知识解出来的?你知道每一步的依据吗?体现了数学中的哪些思想方法?
二.自我检测书本89页练习1.2
3.知新有疑
【范例精析】:
在山脚C处测得山顶A的仰角为45°。问题如下:
1.沿着水平地面向前300米到达D点,在D点测得山顶A的仰角为60 °,求山高AB。
2.沿着坡角为30 °的斜坡前进300米到达D点,在D点测得山顶A的仰角为60 ° ,求山高AB。
【达标测评】:
1、直升飞机在高为200米的大楼AB上方P点处,从大楼的顶部和底部测得飞机的仰角为30°和45°,求飞机的高度PO .
2、如图所示,小杨在广场上的A处正面观测一座楼房墙上的广告屏幕,测得屏幕下端D处的仰角为30o,然后他正对大楼方向前进5m到达B处,又测得该屏幕上端C处的仰角为45o.若该楼高为26.65m,小杨的眼睛离地面1.65m,广告屏幕的上端与楼房的顶端平齐.求广告屏幕上端与下端之间的距离(≈1.732,结果精确到0.1m).
3.某旅游区有一个景观奇异的望天洞,点是洞的入口,游人从入口进洞游览后,可经山洞到达山顶的出口凉亭处观看旅游区风景,最后坐缆车沿索道返回山脚下的处.在同一平面内,若测得斜坡的长为100米,坡角,在处测得的仰角,在处测得的仰角,过点作地面的垂线,垂足为.
(1)求的度数;
(2)求索道的长.(结果保留根号)
4.书本92-93页3.4.7
【小结反思】
28.2 解直角三角形的应用(2)----方位角教学案
执笔: 王梅 初审 :王银 复审:王富贵
授课人: 课型 :新授 课时:1课时
学生姓名: 班级: 小组:
【教学目标】
1.使学生理解方位角概念的意义,并能适当的选择锐角三角函数关系式去解决有关直角三角形实际问题;
2. 培养学生将实际问题抽象为数学问题(画出平面图形?转化为解直角三角形)的能力
【教学重点】用三角函数有关知识解决方位角的实际问题
【教学难点】学会准确分析问题并将实际问题转化成数学模型
【自主探究】
一. 导引自学:阅读书本P89例5,思考以下问题
1.(1)方位角的定义是什么?
(2)画出以下方位角;南偏东300 ; 南偏西600;北偏西150 ; 东北方向。
(3)A点在B点的南偏东360,,则B点在A点的什么方向?
2.例2中如何把实际问题转化成几何问题?可将问题到一个什么几何图形中解决?根据示意图,用什么知识解出来的?你知道每一步的依据吗?体现了数学中的哪些思想方法?
3.你知道利用直角三角形的知识解决实际问题的一般步骤吗?
二.自我检测:
1.如图,太阳光线与地面成60°角,一棵倾斜的大树与地面成30°角,这时测得大树在地面上的影子约为10米,则大树的高约为________米.(结果保留根号)
2. 王英同学从A地沿北偏西60o方向走100m到B地,再从B地向正南方向走200m到C地,此时王英同学离A地 ( )
A.150m B.m C.100 m D.m
3.如图所示,海上有一灯塔P,在它周围3海里处有暗礁.一艘客轮以9海里/时?的速度由西向东航行,行至A点处测得P在它的北偏东60°的方向,继续行驶20分钟后,到达B处又测得灯塔P在它的北偏东45°方向.问客轮不改变方向继续前进有无触礁的危险?
4.书本91页练习1
三.知新有疑
【范例精析】
如图,某货船以20海里/时的速度将一批重要物资由A处运往正西方向的B处,经16小时的航行到达,到达后必须立即卸货.此时.接到气象部门通知,一台风中心正以40海里/时的速度由A向北偏西60°方向移动,距台风中心200海里的圆形区域(包括边界)均受到影响.
(1)B处是否会受到台风的影响?请说明理由.
(2)为避免受到台风的影响,该船应在多少小时内卸完货物?(供选用数据:≈1.4, ≈1.7)
【达标测评】
1.上午10点整,一渔轮在小岛O的北偏东30°方向,距离等于10海里的A处,正以每小时10海里的速度向南偏东60°方向航行.那么渔轮到达小岛O的正东方向是什么时间?(精确到1分).
2、在东西方向的海岸线上有一长为1km的码头MN(如图),在码头西端M 的正西19.5 km 处有一观察站A.某时刻测得一艘匀速直线航行的轮船位于 A 的北偏西30°,且与A相距40km的B处;经过1小时20分钟,又测得该轮船位于A的北偏东60°,且与A相距km的C处.
(1)求该轮船航行的速度(保留精确结果);
(2)如果该轮船不改变航向继续航行,那么轮船能否正
好行至码头MN靠岸?请说明理由.
3.书本93页习题9
【自我反思】
1、知识技能: 。
2、思想方法: 。
28.2解直三角形应用(三)----坡度问题
执笔: 王梅 初审 :王增梅 复审:王富贵
授课人: 课型 :新授 课时:1课时
学生姓名: 班级: 小组:
【教学目标】
1.巩固用三角函数有关知识解决问题,学会解决坡度问题.
2.逐步培养学生分析问题、解决问题的能力;渗透数形结合的数学思想和方法.
3.培养学生用数学的意识,渗透理论联系实际的观点.
【教学重点】:解决有关坡度的实际问题.
【教学难点】:理解坡度的有关术语.
【自主探究】
一.导引自学:自学书本p90-91思考以下问题
1.坡面的铅直高度h和水平宽度的比叫做坡度(或叫做坡比),
2.一般用i表示。即i=( )常写成i=1:m的形式如i=1:2.5把坡面与水平面的夹角α叫做坡角.
3.结合图形思考,坡度i与坡角α之间具有什么关系?
二.自我检测:
1.一段坡面的坡角为60°,则坡度i=______;
______,坡角______度.
2.书本91页练习2
3.如图,一水坝横断面为等腰梯形ABCD,斜坡AB的坡度为1∶,坡面AB的水平宽度为3米,上底宽AD为4米,求坡角B,坝高AE和坝底宽BC各是多少?
三.知新有疑
【范例精析】
某海港区为提高某段海堤的防海潮能力,计划将100米的一段堤(原海堤的横断面如图中的梯形ABCD)的堤面加宽1米,背水坡度由原来的1:1改成1:2。已知原背水坡长AD= 米,求完成这一工程所需的土方数。
【达标测评】
1、如图,沿江堤坝的横断面是梯形ABCD,坝顶AD=4m,坝高AE=6 m,斜坡AB的坡比,∠C=60°,求斜坡AB、CD的长。
2、同学们,如果你是修建三峡大坝的工程师,现在有这样一个问题请你解决:如图水库大坝的横断面是梯形,坝顶宽6m,坝高23m,斜坡AB的坡度i=1∶3,斜坡CD的坡度i=1∶2.5,求斜坡AB的坡面角α,坝底宽AD和斜坡AB的长(精确到0.1m)
3.书本92-93习题5.6.8
.
【课堂小结】:
1.把实际问题转化成数学问题,转化包括两个方面:一是(将实际问题的图形转化为几何图形,画出正确的示意图);二是(将已知条件转化为示意图中的边、角或它们之间的关系).
2.把数学问题转化成解直角三角形问题,如果示意图不是直角三角形,可(添加适当的辅助线),画出(直角)三角形.
数学活动——利用测角仪测量物体的高度导学案
执笔: 谢力 初审 :王银 复审:王富贵
授课人:谢力 课型 :新授 课时:1课时
学生姓名: 班级: 小组:
【学习目标】
1、通过测量和计算大树、塔高度的活动,巩固三角函数的有关知识。
并在活动中积累数学活动经验。
2、通过测量活动,使我初步学会数学建模的方法.,提高综合运用知识的能力.
【教学重点】掌握利用测角仪测量物体的高度的操作方法,并能运用三角函数的知识解决实际问题。
【教学难点】学会如何在实际问题中构造直角三角形,建立三角函数的模型和图形模型。
【自主探究】
一、导引自学:自学课本98——99页完成下列问题
1、右图中仪器的名称是 ,它是用来 。
2、用手中的量角器制作一个1题中的测量工具。
3、测量活动:
活动一:利用制作的测量工具测量大树的高度。
请你设计一个测量方案,亲自测量后,回答下列问题:
(1)在你设计的方案中,选用的测量工具有
(2)你需要用 测得你到树根的距离是 ,用 测量你看到的树的顶端的仰角是 ,还需要知道 。
(3)在右图中画出你的测量方案示意图;
(4)写出求树高的算式:AB=
活动二:利用制作的测量工具测量塔的高度。
请设计出实际操作方案,并根据方案回答问题:
(1)在你设计的方案中,选用的测量工具是
(用工具的序号填写)
(2)在右图中画出你的测量方案示意图;
(3)你需要测得示意图中的哪些数据,并分别用a、b、c、α等表示测得的数据:
(4)写出求塔高的算式:
问题:活动一与活动二的方法有何优、缺点?还有别的测量方法吗?
二、自我检测:
如图,小明欲利用测角仪测量树的高度.已知他离树的水平距离BC为10m,测角仪的高度CD为1.5m,测得树顶A的仰角为33°.求树的高度AB.(参考数据:sin33°≈0.54,cos33°≈0.84,tan33°≈0.65)
三、知新有疑 :通过自学
我的收获是:
我的疑惑是:
【范例精析】
蒿坪中学九年级的李明同学想知道学校旗杆的高度,但手中只有刚制作的测角仪,在下列情形下他能测出旗杆的高度吗?(测出的角用α、β表示)
(1)他站在距旗杆15米的教学楼三楼上,却不知三层楼的高度,此时他是怎样测量旗杆的高度呢?
(2)他站在距旗杆15米远,且高为24米的教学楼楼顶上,他又是怎么测出的呢?
(3)这次他站在离建筑物15米的地面上测,可是建筑物将旗杆的一部分挡住了,已知李明同学的身高是1.6米,你知道他是怎么测得吗?
【达标测评】
1、小明利用所学的数学知识测量生活中一建筑物的高AB.(1)请帮小明写出具体的测量方法?并画图表示(角用1、2、3表示,线段用a、b、c表示)(2)请用你测得的数据帮助小明求出建筑物AB的高.
【小结反思】
学生自由发言,总结学习收获体验;
解直角三角形复习(1)
执笔:王银 初审:王梅 复审:王富贵
授课人: 课型:复习课 课时:1
学生姓名: 班级: 小组:
【教学目标】:通过复习,使学生系统地掌握本章知识。在系统复习知识的同时,使学生能够灵活运用知识解决问题。
【教学重点】:通过复习,使学生系统地掌握本章知识。
【教学难点】: 在系统复习知识的同时,使学生能够灵活运用知识解决问题。
一、自主探究
1.本章学习了哪些知识,用到了哪些数学思想方法?
2.自己尝试画出知识结构图
【范例精析】:
例1.Rt△ABC中,∠C=90°,∠B=60°,两直角边的和为14,求这个直角三角形的面积。
例2.如图,AC⊥BC,cos∠ADC=,∠B=30°AD=10,求 BD的长。
例3.Rt△ABC中,∠C=90°,AC=8,∠A的平分线AD=,求∠B的度数以及边BC、AB的长。
【当堂检测】.
一、选择题
1、如图,点P(3,4)是∠α的边OA上的一点,则Sinα= .
A、 B、 C、 D、
2、某市为改善交通状况,修建了大量的高架桥,一汽车在坡度为300的笔直高架桥点A开始爬行,行驶了150米到达B点,这时汽车离地面高度为 米.
A、300 B、150 C、75 D、50
3、把Rt△ABC的各边都扩大3倍得Rt△A/B/C/,那么锐角A、A/ 的余弦值的关系是 .
A、cosA = cosA/ B、cosA = 3cosA/
C、3cosA = cosA/ D、不能确定
4、已知锐角A的cosA≤,则锐角A的取值范围是 .
A、0<A≤600 B、600≤A<900 C、0<A≤300 D、300≤A<900
5、王英从A地向北偏西600方向走100米到B地,再从B地向正南方向走200米到C地,此时王英离A地有 米.
A、50 B、100 C、150 D、100
6、在Rt△ABC中,∠C = 900,tanA = ,则SinB = .
A、 B、 C、 D、
7、在Rt△ABC中,∠C = 900,CD是斜边AB上的中线,CD = 2,AC = 3,则 SinB = .
A、 B、 C、 D、
8.Rt△ABC中,∠C=90°,∠A=30°,∠A、∠B、∠C所对的边为a、b、c,则a:b:c=( )
A、1:2:3 B、1: : C、1: :2 D、1:2:
9.下列说法正确的是( )
A.在△ ABC中,若∠A的对边是3,一条邻边是5,则tanA=
B.将一个三角形的各边扩大3倍,则其中一个角的正弦值也扩大3倍
C.在锐角△ ABC中,已知∠A=60°,那么cosA=
D.一定存在一个锐角A,使得sinA=1.23
10.已知锐角α,且sinα=cos37°,则a等于( )
A.37° B.63° C.53° D.45°
11.当锐角α>30°时,则cosα的值是( )
A.大于 B.小于 C.大于 D.小于
12.求值:
(1) 6tan2 30°-sin 60°+2tan45°
(2)
解直角三角形复习(2)
执笔:王银 初审:王梅 复审:王富贵
授课人: 课型:复习课 课时:1
学生姓名: 班级: 小组:
【教学目标】:
使学生掌握直角三角形的边与边,角与角,边与角的关系,能应用这些关系解决相关的问题,进一步培养学生应用知识解决问题的能力。
【教学重点】:学生掌握直角三角形的边与边,角与角,边与角的关系
【教学难点】:能应用这些关系解决相关的实际问题,进一步培养学生应用知识解决问题的能力。
【自主探究】
1.说一说直角三角形中边角有哪些关系?
2. 说一说仰角.俯角.方位角.坡角的定义,画图说明.
3. 你知道利用直角三角形的知识解决实际问题的一般步骤吗?
【自我检测】
1.甲、乙、丙三个梯子斜靠在一堵墙上(梯子顶端靠墙), 小明测得:甲与地面的夹角为60°;乙的底端距离墙脚米,且顶端距离墙脚3米;丙的坡度为。那么,这三张梯子的倾斜程度( )
A.甲较陡 B.乙较陡 C.丙较陡 D.一样陡
2、小琳家在门前O处,有一条东西走向的公路,经测得有一水塔A在她家北偏东
600的500米处,那么水塔所在的位置到公路的距离AB = 米.
A、250 B、250 C、 D、250
3.如图,沿AC方向开山修路,为了加快施工进度,要在山的另一边同时施工,现在从AC上取一点B,使得∠ABD=145°,BD=500米,∠D=55°,要使A、C、E在一条直线上,那么开挖点E离点D的距离是( )
A.500sin55°米 B.500cos55°米
C.500tan55°米; D.米
4、如图,轮船由南向北航行到O处,发现与轮船相距40海里的A岛在北偏东330方向上的A岛周围20海里水域内有暗礁,若不改变航向,则轮船 触礁的危险.(有或无)
5.若A在B的北偏东20°处,那么B在A的 方向上.
6.某山路的路面坡度ⅰ=1:,沿此山路向前走200米,则人升高了___ __米.
7.每周一学校都要举行庄严的升国旗仪式,让我们感受到了国旗的神圣.升国旗时,某同学站在离旗杆底部24米处行注目礼,当国旗升至旗杆顶端时,该同学视线的仰角恰为30°,若双眼离地面1.5米,则旗杆的高度为__ ____米。(用含根号的式子表示)
【范例精析】 例1.北部湾海面上,一艘解放军军舰正在基地A的正东方向且距离A地40海里的B处训练。突然接到基地命令,要该舰前往C岛,接送一名病危的渔民到基地医院救治。已知C岛在A的北偏东方向60°,且在B的北偏西45°方向,军舰从B处出发,平均每小时行驶20海里,需要多少时间才能把患病渔民送到基地医院?(精确到0.1小时)
例3.如图5,某防洪指挥部发现长江边一处长500米,高I0米,背水坡的坡角为45°的防洪大堤(横断面为梯形ABCD)急需加固.经调查论证,防洪指挥部专家组制定的加固方案是:沿背水坡面用土石进行加固。并使上底加宽3米,加固后背水坡EF的坡比i=1:。
(I)求加固后坝底增加的宽度AF;
(2)求完成这项工程需要土石多少立方米?(结果保留根号)
【当堂检测】:
1.如图,城市规划期间,欲拆除一电线杆AB,已知电线杆AB距水平距离14m的D处有有大坝,背水坡CD的坡度,坝高C F为2m,在坝顶C处测地杆顶的仰角为,D、E之间是宽度位2m的人行道。试问:在拆除电线杆AB时,为确保行人安全是否需要将此人行道封闭?请说明你的理由(在地面上以B为圆心,以AB为半径的图形区域为危险区域,)。
2、在某建筑物AC上挂着“多彩贵州” 的宣传条幅BC,小明站在点F处,看条幅顶端B,测得仰角为300,再往条幅方向前行20米到达点E处,看到条幅顶端B,测得仰角为600,求宣传条幅BC的长. (小明的身高不计,结果精确到O.1米)
第28章锐角三角函数单元测试卷
一、选择(每题 3分,合计 30分 )
1. 在,,,则等于( )
A. B. C. D.1
2. 在Rt△ABC中 ,,,则的值是( )
A. B. C. D.
3. 中,,且,则等于( )
A. B. C. D.
4. 等腰三角形的边长为6,8,则底角的余弦是( )
A. B. C. D.和
5. 某市在旧城改造中,计划在市内一块如图1所示三角形空地上种植草皮以美化环境,已知这种草皮每平方米售价元,则购买这种草皮至少需要( )
A.450元 B.元
C.元 D.元
6.如图2,一个钢球沿坡角的斜坡向上滚动了米,此时钢球距地面的高度是( )米.
A. B. C. D.
7. 若,则以∠A、∠B为内角的一定是( ).
A.等腰三角形 B.等边三角形 C.直角三角形 D.锐角三角形
8. .如图3,在中,,于,若,
,则的值为( ).
A. B. C. D.
9. 如图4,有两条宽度为1的带子,相交成角,那么重叠部分(阴影)
的面积是( ).
A.1 B. C. D.
10. 如图5,在高楼前点测得楼顶的仰角为,向高楼前
进60米到点,又测得仰角为,则该高楼的高度大
约为( ).
A.82米 B.163米 C.52米 D.70米
二、填空(每题3分,合计21分)
1. 在△ABC中,若∠A=30°,∠B=45°,AC=,则BC=
2. .在中,,,则
3. 离旗杆20米处的地方用测角仪测得旗杆顶的仰角为, 如果测角仪高为1.5米.那么旗杆的高 为米(用含的三角函数表示)。
4. 在正方形网格中,的位置如图6所示,则的值为______.
5. 如图7,在坡度为的山坡上种树,要求株距(相邻两树间的水平距离)是6米,斜坡上相邻两树间的坡面距离是 米
6. 如图8,已知正方形的边长为3,如果将线段绕点旋转后,点落在延长线上的点处,那么 .
7. 如图9,钓鱼竿长,露在水面上的鱼线长,某钓者想看看鱼钓上的情况,把鱼竿转动到的位置,此时露在水面上的鱼线为,则鱼竿转过的角度是________.
三、解答题
1. 计算求值:(每题5分,合计20分)
(1); (2);
(3); (4)
2. 如图10,在平地处测得树顶的仰角为,向树前进10m,到达处,再测得树顶的仰角为,求树高(结果保留根号).(9分)
3. 如图11,某边防巡逻队在一个海滨浴场岸边的A点处发现海中的B点有人求救,便立即派三名救生员前去营救.1号救生员从A点直接跳入海中;2号救生员沿岸边(岸边看成是直线)向前跑到C点,再跳入海中;3号救生员沿岸边向前跑3 0 0米到离B点最近的D点,再跳人海中.救生员在岸上跑的速度都是6米/秒,在水中游泳的速度都是2米/秒.若,,三名救生员同时从A点出发,请说明谁先到达营救地点B. (参考数据≈1.4,≈1.7) (10分)
4. 如图12所示,某超市在一楼至二楼之间安装有电梯,天花板与地面平行,请你根据图中数据计算回答:
小敏身高1.78米,她乘电梯会有碰头危险吗?姚明身高2.29米,他乘电梯会有碰头危险吗?
(可能用到的参考数值:,,)(10分)
