数学高中苏教版选修(2-1)3.1《空间向量及其运算》课件2
文档属性
| 名称 | 数学高中苏教版选修(2-1)3.1《空间向量及其运算》课件2 |

|
|
| 格式 | zip | ||
| 文件大小 | 170.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-07 00:00:00 | ||
图片预览





文档简介
课件34张PPT。空间向量
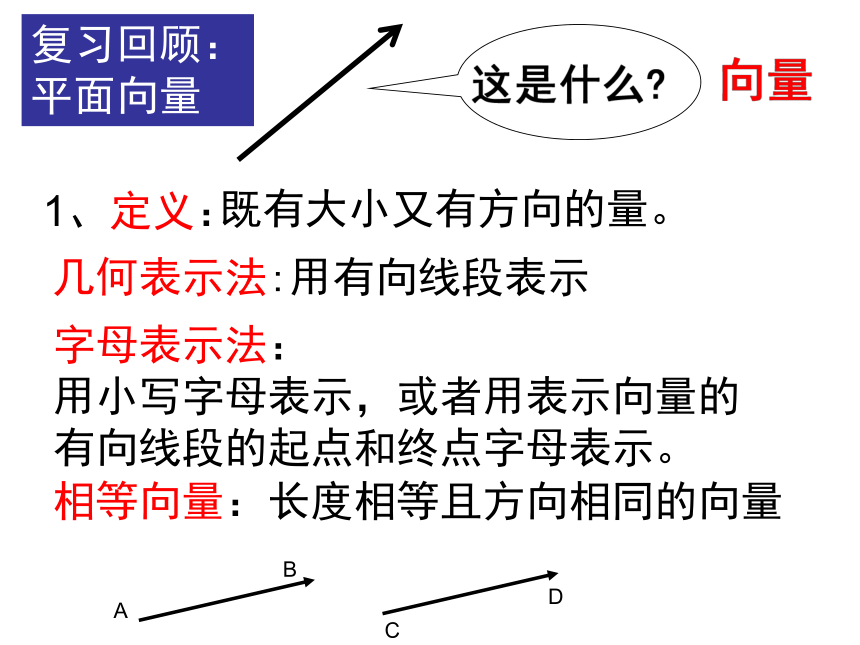
及其运算复习回顾:
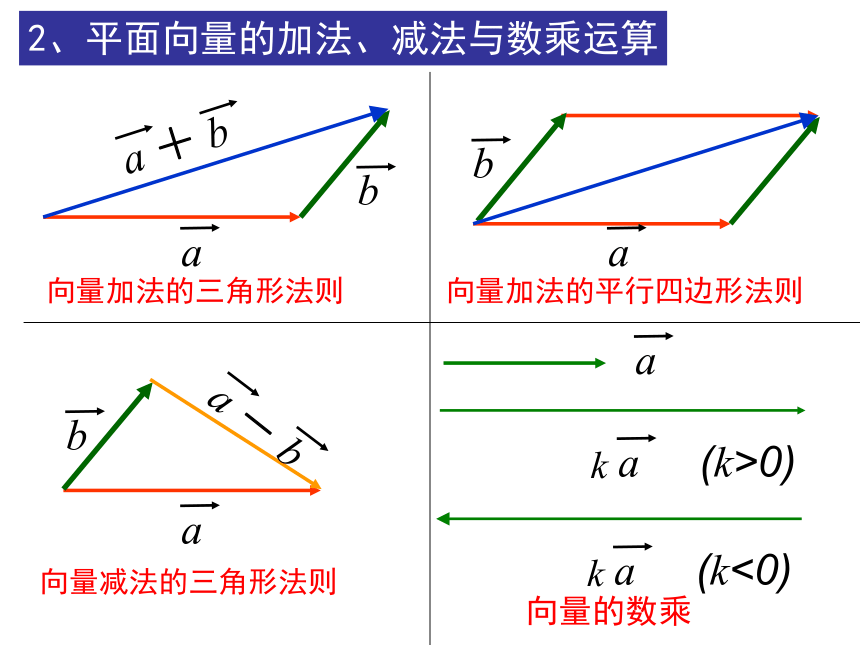
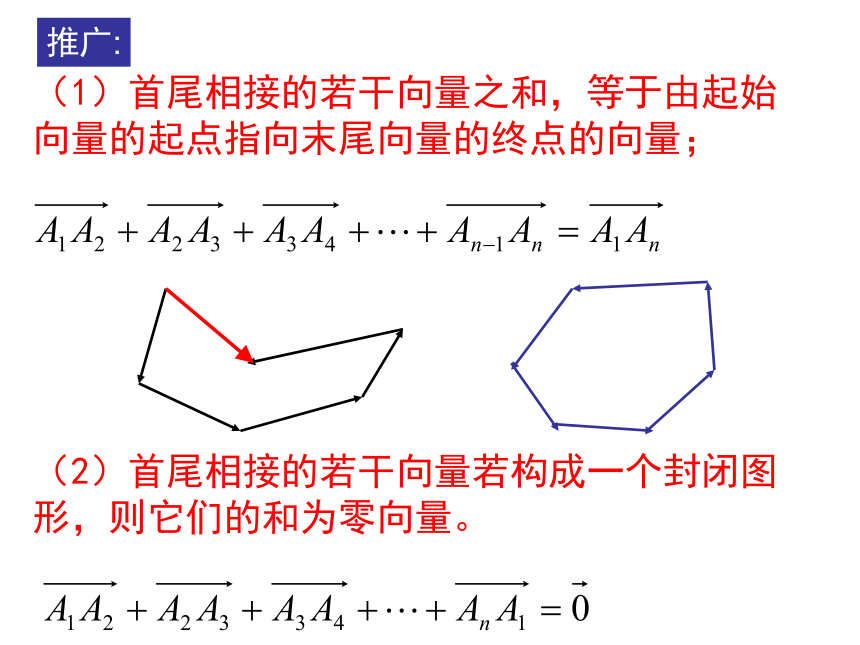
平面向量1、定义:既有大小又有方向的量。2、平面向量的加法、减法与数乘运算向量加法的三角形法则3、平面向量的加法、减法与数乘运算律推广:(1)首尾相接的若干向量之和,等于由起始
向量的起点指向末尾向量的终点的向量;(2)首尾相接的若干向量若构成一个封闭图
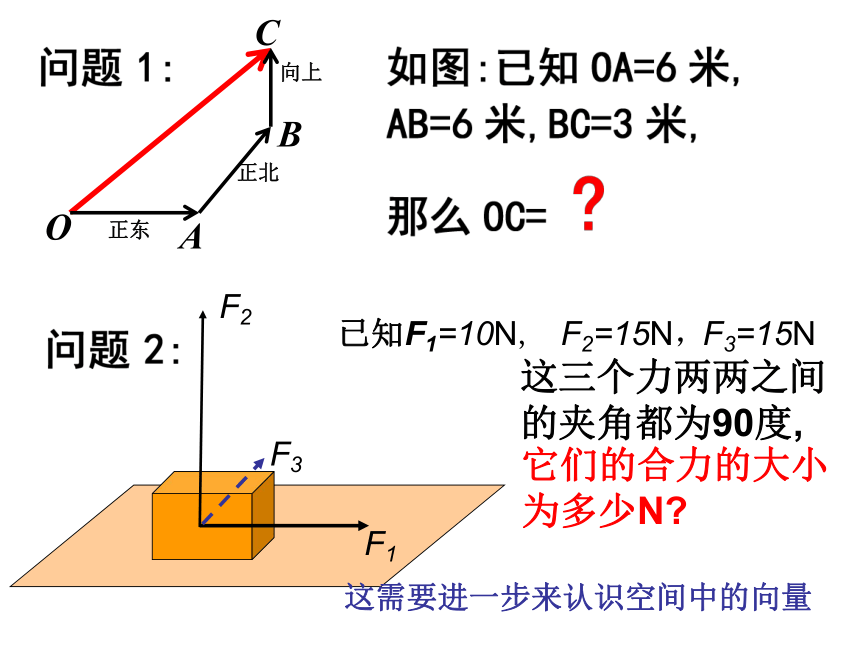
形,则它们的和为零向量。F3F3=15N已知F1=10N,F2=15N,F1F2这三个力两两之间的夹角都为90度,它们的合力的大小为多少N?这需要进一步来认识空间中的向量起点终点平面向量概念加法
减法
数乘
运算运
算
律定义表示法相等向量减法:三角形法则加法:三角形法则或
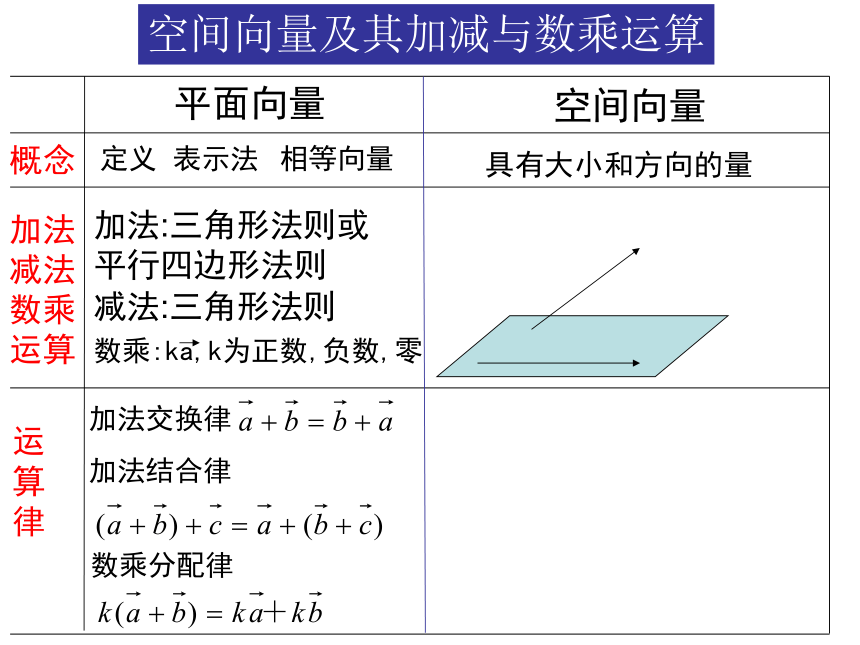
平行四边形法则空间向量及其加减与数乘运算空间向量具有大小和方向的量数乘:ka,k为正数,负数,零加法交换律加法结合律数乘分配律CABD平面向量概念加法
减法
数乘
运算运
算
律定义表示法相等向量减法:三角形法则加法:三角形法则或
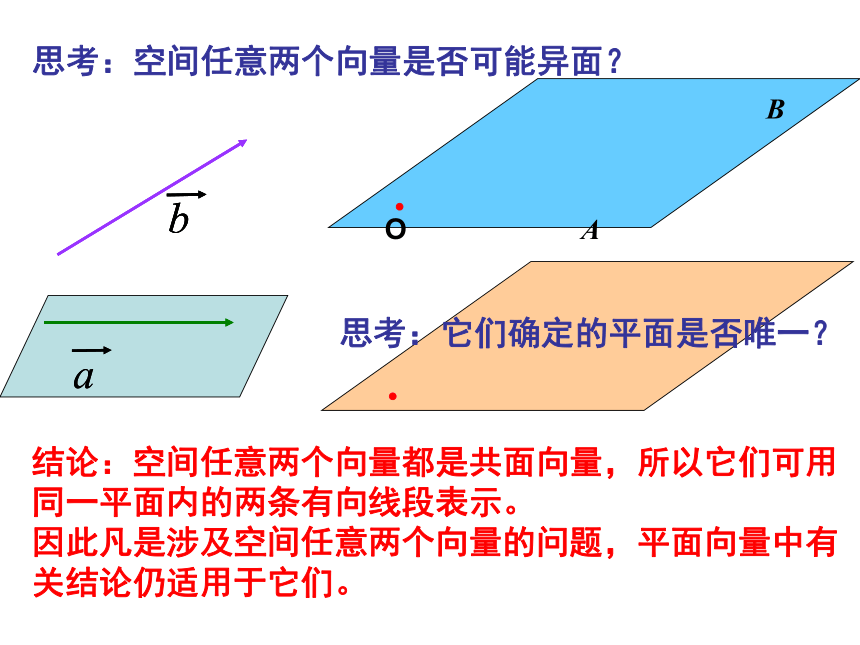
平行四边形法则空间向量及其加减与数乘运算空间向量具有大小和方向的量数乘:ka,k为正数,负数,零加法交换律加法结合律数乘分配律OABC空间向量的数乘空间向量的加减法OAB结论:空间任意两个向量都是共面向量,所以它们可用
同一平面内的两条有向线段表示。
因此凡是涉及空间任意两个向量的问题,平面向量中有
关结论仍适用于它们。思考:它们确定的平面是否唯一?思考:空间任意两个向量是否可能异面?平面向量概念加法
减法
数乘
运算运
算
律定义表示法相等向量减法:三角形法则加法:三角形法则或
平行四边形法则空间向量及其加减与数乘运算空间向量具有大小和方向的量数乘:ka,k为正数,负数,零加法交换律加法结合律数乘分配律加法:三角形法则或
平行四边形法则减法:三角形法则数乘:ka,k为正数,负数,零加法结合律成立吗?OBCOBC(平面向量)向量加法结合律在空间中仍成立吗?AAOABCOABC(空间向量)向量加法结合律:空间中推广:(1)首尾相接的若干向量之和,等于由起始
向量的起点指向末尾向量的终点的向量;(2)首尾相接的若干向量若构成一个封闭图
形,则它们的和为零向量。平面向量概念加法
减法
数乘
运算运
算
律定义表示法相等向量减法:三角形法则加法:三角形法则或
平行四边形法则空间向量具有大小和方向的量数乘:ka,k为正数,负数,零加法交换律加法结合律数乘分配律小结类比思想 数形结合思想数乘:ka,k为正数,负数,零?例如:定义: 我们知道平面向量还有数乘运算.
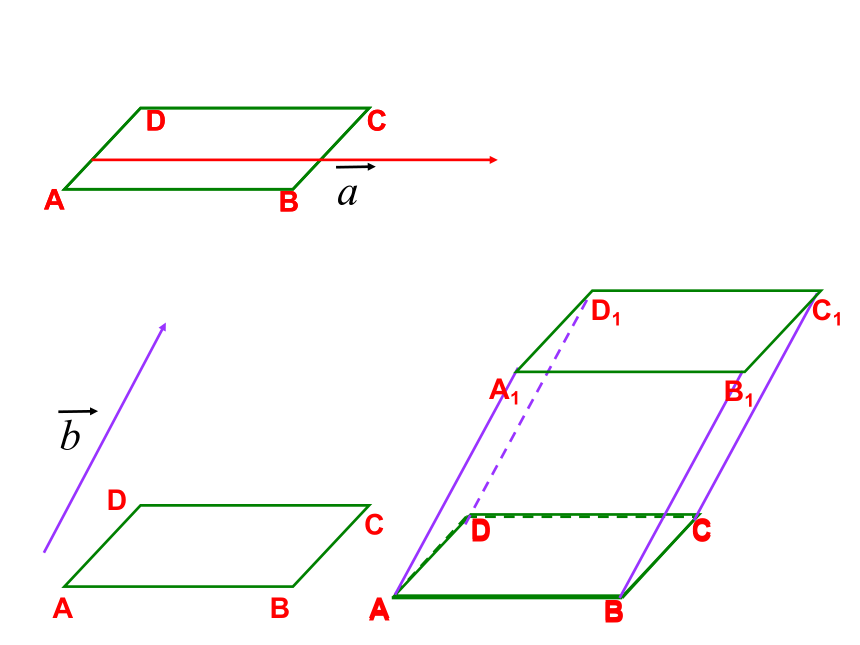
类似地,同样可以定义空间向量的数乘运算,其运算律是否也与平面向量完全相同呢? 显然,空间向量的数乘运算满足分配律及结合律例1:已知平行六面体ABCD-A1B1C1D1,化简下列向量
表达式,并标出化简结果的向量。(如图)ABCD平行六面体:平行四边形ABCD平移向量
到A1B1C1D1的轨迹所形成的几何体.记做ABCD-A1B1C1D1例1:已知平行六面体ABCD-A1B1C1D1,化简下列向量
表达式,并标出化简结果的向量。(如图)GM 始点相同的三个不共面向量之和,等于以这三个向量
为棱的平行六面体的以公共始点为始点的对角线所示向量F1F2F1=10NF2=15NF3=15N例2:已知平行六面体ABCD-A1B1C1D1,
求满足下列各式的x的值。例2:已知平行六面体ABCD-A1B1C1D1,
求满足下列各式的x的值。例2:已知平行六面体ABCD-A1B1C1D1,
求满足下列各式的x的值。例2:已知平行六面体ABCD-A1B1C1D1,
求满足下列各式的x的值。ABMCGD练习1在空间四边形ABCD中,点M、G分别是BC、CD边的中点,化简ABMCGD(2)原式练习1在空间四边形ABCD中,点M、G分别是BC、CD边的中点,化简ABCDDCBA练习2在立方体AC1中,点E是面AC’ 的中心,求下列各式中的x,y.EABCDDCBA练习2E在立方体AC1中,点E是面AC’ 的中心,求下列各式中的x,y.ABCDDCBA练习2E在立方体AC1中,点E是面AC’ 的中心,求下列各式中的x,y.作业
及其运算复习回顾:
平面向量1、定义:既有大小又有方向的量。2、平面向量的加法、减法与数乘运算向量加法的三角形法则3、平面向量的加法、减法与数乘运算律推广:(1)首尾相接的若干向量之和,等于由起始
向量的起点指向末尾向量的终点的向量;(2)首尾相接的若干向量若构成一个封闭图
形,则它们的和为零向量。F3F3=15N已知F1=10N,F2=15N,F1F2这三个力两两之间的夹角都为90度,它们的合力的大小为多少N?这需要进一步来认识空间中的向量起点终点平面向量概念加法
减法
数乘
运算运
算
律定义表示法相等向量减法:三角形法则加法:三角形法则或
平行四边形法则空间向量及其加减与数乘运算空间向量具有大小和方向的量数乘:ka,k为正数,负数,零加法交换律加法结合律数乘分配律CABD平面向量概念加法
减法
数乘
运算运
算
律定义表示法相等向量减法:三角形法则加法:三角形法则或
平行四边形法则空间向量及其加减与数乘运算空间向量具有大小和方向的量数乘:ka,k为正数,负数,零加法交换律加法结合律数乘分配律OABC空间向量的数乘空间向量的加减法OAB结论:空间任意两个向量都是共面向量,所以它们可用
同一平面内的两条有向线段表示。
因此凡是涉及空间任意两个向量的问题,平面向量中有
关结论仍适用于它们。思考:它们确定的平面是否唯一?思考:空间任意两个向量是否可能异面?平面向量概念加法
减法
数乘
运算运
算
律定义表示法相等向量减法:三角形法则加法:三角形法则或
平行四边形法则空间向量及其加减与数乘运算空间向量具有大小和方向的量数乘:ka,k为正数,负数,零加法交换律加法结合律数乘分配律加法:三角形法则或
平行四边形法则减法:三角形法则数乘:ka,k为正数,负数,零加法结合律成立吗?OBCOBC(平面向量)向量加法结合律在空间中仍成立吗?AAOABCOABC(空间向量)向量加法结合律:空间中推广:(1)首尾相接的若干向量之和,等于由起始
向量的起点指向末尾向量的终点的向量;(2)首尾相接的若干向量若构成一个封闭图
形,则它们的和为零向量。平面向量概念加法
减法
数乘
运算运
算
律定义表示法相等向量减法:三角形法则加法:三角形法则或
平行四边形法则空间向量具有大小和方向的量数乘:ka,k为正数,负数,零加法交换律加法结合律数乘分配律小结类比思想 数形结合思想数乘:ka,k为正数,负数,零?例如:定义: 我们知道平面向量还有数乘运算.
类似地,同样可以定义空间向量的数乘运算,其运算律是否也与平面向量完全相同呢? 显然,空间向量的数乘运算满足分配律及结合律例1:已知平行六面体ABCD-A1B1C1D1,化简下列向量
表达式,并标出化简结果的向量。(如图)ABCD平行六面体:平行四边形ABCD平移向量
到A1B1C1D1的轨迹所形成的几何体.记做ABCD-A1B1C1D1例1:已知平行六面体ABCD-A1B1C1D1,化简下列向量
表达式,并标出化简结果的向量。(如图)GM 始点相同的三个不共面向量之和,等于以这三个向量
为棱的平行六面体的以公共始点为始点的对角线所示向量F1F2F1=10NF2=15NF3=15N例2:已知平行六面体ABCD-A1B1C1D1,
求满足下列各式的x的值。例2:已知平行六面体ABCD-A1B1C1D1,
求满足下列各式的x的值。例2:已知平行六面体ABCD-A1B1C1D1,
求满足下列各式的x的值。例2:已知平行六面体ABCD-A1B1C1D1,
求满足下列各式的x的值。ABMCGD练习1在空间四边形ABCD中,点M、G分别是BC、CD边的中点,化简ABMCGD(2)原式练习1在空间四边形ABCD中,点M、G分别是BC、CD边的中点,化简ABCDDCBA练习2在立方体AC1中,点E是面AC’ 的中心,求下列各式中的x,y.EABCDDCBA练习2E在立方体AC1中,点E是面AC’ 的中心,求下列各式中的x,y.ABCDDCBA练习2E在立方体AC1中,点E是面AC’ 的中心,求下列各式中的x,y.作业
