数学高中苏教版选修(2-1)3.1《空间向量及其运算》课件
文档属性
| 名称 | 数学高中苏教版选修(2-1)3.1《空间向量及其运算》课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 166.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-07 00:00:00 | ||
图片预览



文档简介
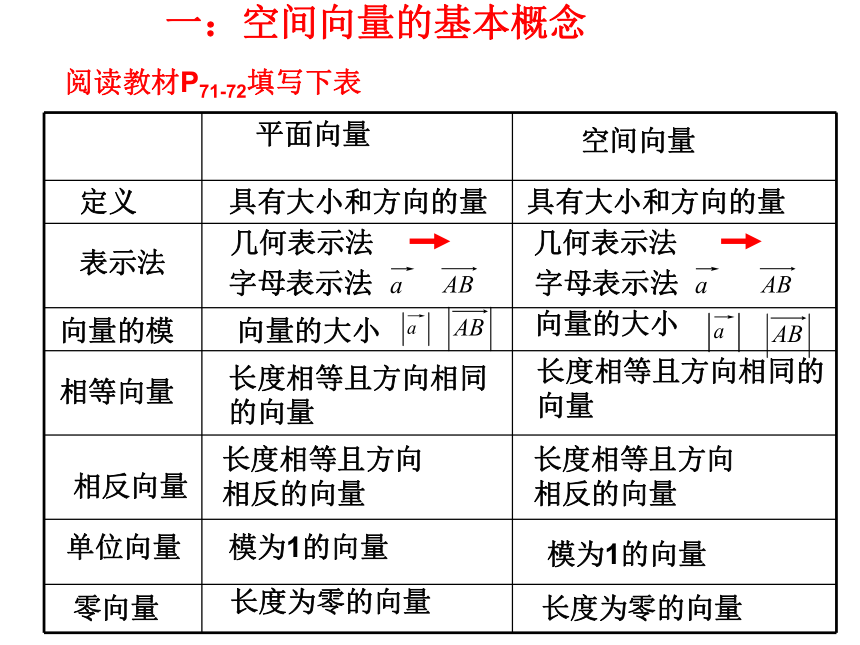
课件27张PPT。空间向量及运算阅读教材P71-72填写下表平面向量空间向量具有大小和方向的量具有大小和方向的量 几何表示法几何表示法字母表示法 字母表示法 向量的大小 向量的大小 长度为零的向量 长度为零的向量模为1的向量模为1的向量长度相等且方向
相反的向量长度相等且方向
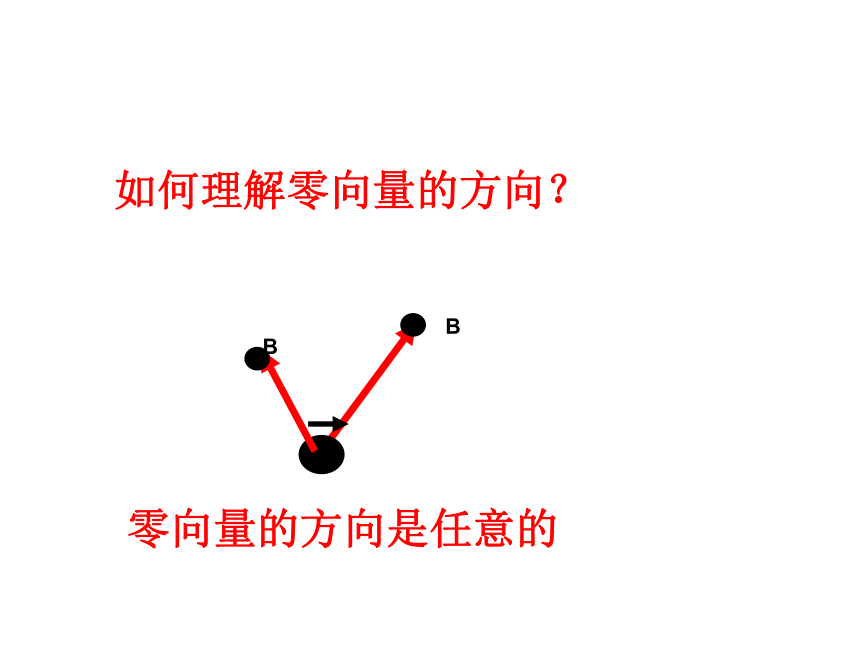
相反的向量长度相等且方向相同 的向量长度相等且方向相同的向量定义表示法向量的模零向量单位向量相反向量相等向量一:空间向量的基本概念ABB零向量的方向是任意的如何理解零向量的方向?例1、给出以下命题:
(1)两个空间向量相等,则它们的起点、终点相同;
(2)若空间向量 满足 ,则 ;
(3)在正方体 中,必有 ;
(4)若空间向量 满足 ,则 ;
(5)空间中任意两个单位向量必相等。
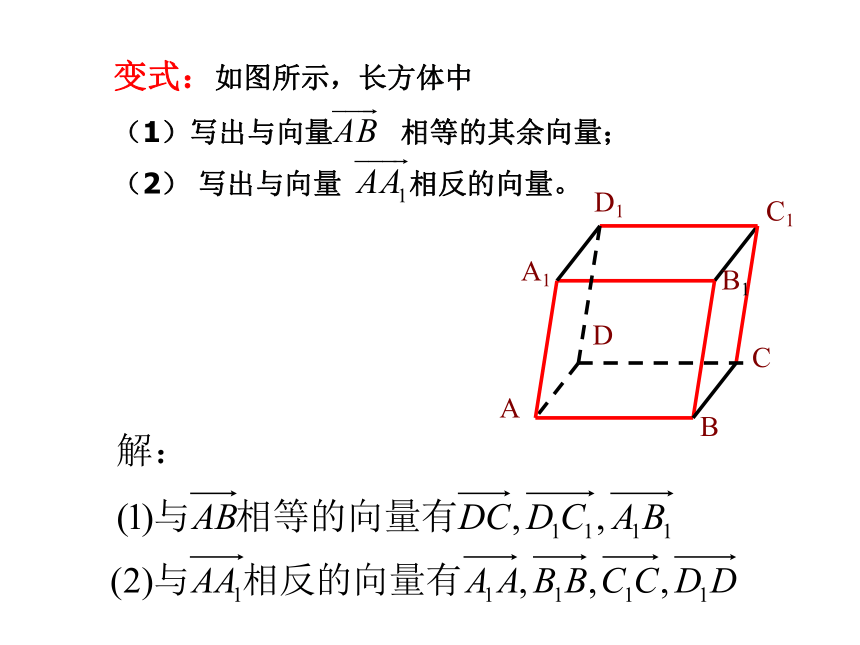
其中不正确命题的个数是———————— (1)(2)(5)变式:如图所示,长方体中
(1)写出与向量 相等的其余向量;
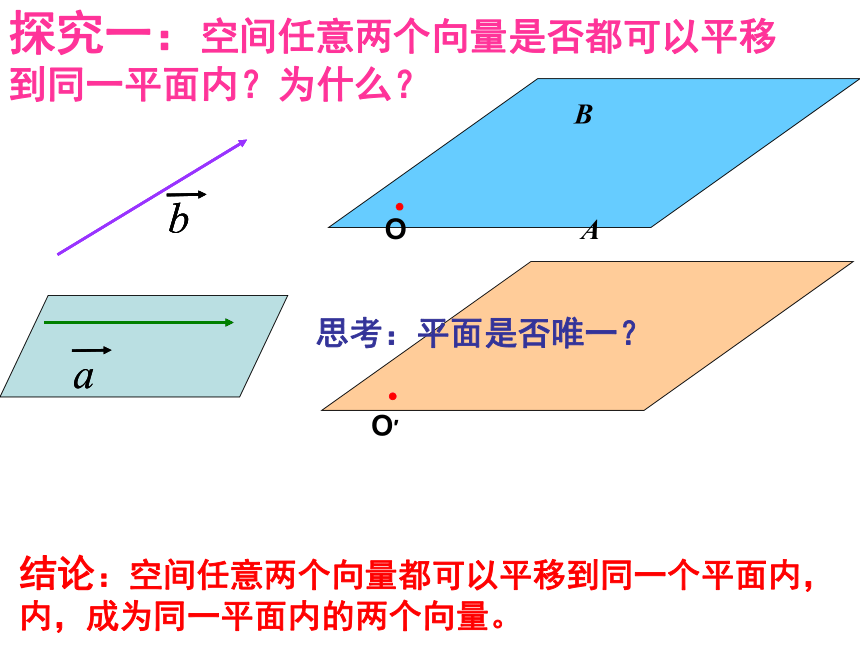
(2) 写出与向量 相反的向量。OAB思考:平面是否唯一?探究一:空间任意两个向量是否都可以平移到同一平面内?为什么?O′结论:空间任意两个向量都可以平移到同一个平面内,
内,成为同一平面内的两个向量。平面向量概念加法
减法
数乘
运算运
算
律定义表示法相等向量减法:三角形法则加法:三角形法则或
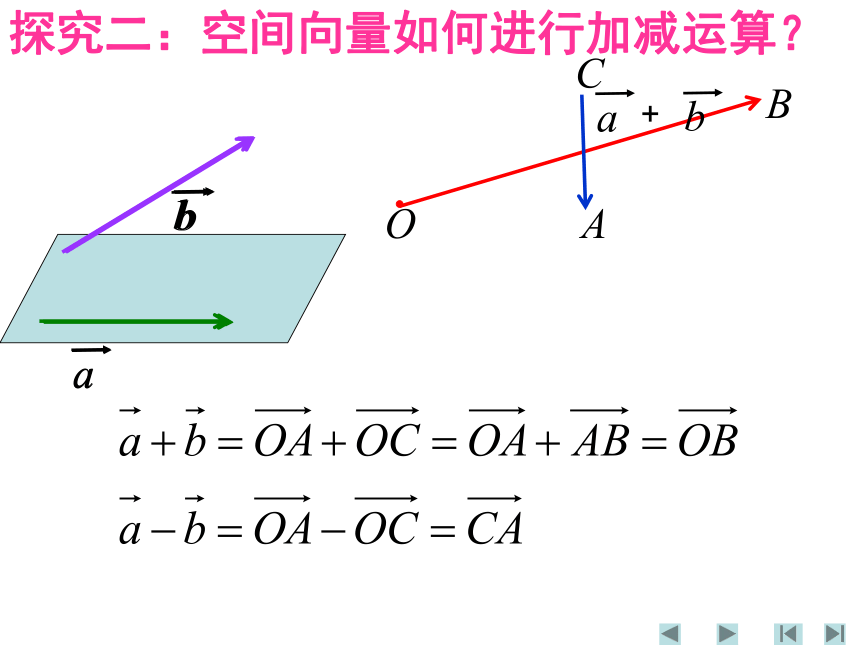
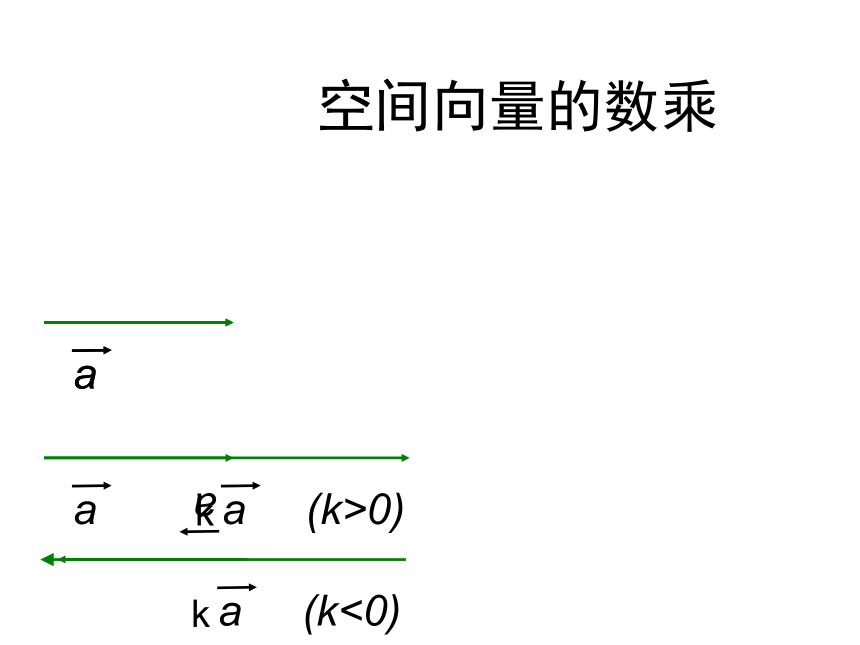
平行四边形法则空间向量及其加减与数乘运算空间向量具有大小和方向的量数乘:ka,k为正数,负数,零加法交换律加法结合律数乘分配律OABC探究二:空间向量如何进行加减运算?空间向量的数乘OABC空间向量加法交换律:探究三:空间向量的加法是否满足交换律?b + aa + b
=OABCOABC(空间向量)空间向量的加法是否满足结合律?=加法交换律:加法结合律:空间向量的加法的运算律:数乘分配律平面向量概念加法
减法
数乘
运算运
算
律定义表示法相等向量减法:三角形法则加法:三角形法则或
平行四边形法则空间向量及其加减与数乘运算空间向量具有大小和方向的量数乘:ka,k为正数,负数,零加法交换律加法结合律数乘分配律加法:三角形法则或
平行四边形法则减法:三角形法则数乘:ka,k为正数,负数,零加法结合律 练一练例1:已知平行六面体ABCD-A1B1C1D1,化简下列向量
表达式,并标出化简结果的向量。(如图)GM 始点相同的三个不共面向量之和,等于以这三个向量
为棱的平行六面体的以公共始点为始点的对角线所示向量例2:已知平行六面体ABCD-A1B1C1D1,
求满足下列各式的x的值。例2:已知平行六面体ABCD-A1B1C1D1,
求满足下列各式的x的值。例2:已知平行六面体ABCD-A1B1C1D1,
求满足下列各式的x的值。例2:已知平行六面体ABCD-A1B1C1D1,
求满足下列各式的x的值。ABMCGD(2)原式练习1在空间四边形ABCD中,点M、G分别是BC、CD
边的中点,化简ABCDDCBA练习2E在立方体AC1中,点E是面AC’ 的中心,求下列各式中的x,y.ABCDDCBA练习2E在立方体AC1中,点E是面AC’ 的中心,求下列各式中的x,y.平面向量概念加法
减法
运算运
算
律定义表示法相等向量减法:三角形法则加法:三角形法则或
平行四边形法则空间向量具有大小和方向的量加法交换律加法结合律小结类比、数形结合数乘分配律数乘分配律作业思考题:考虑空间三个向量共面的充要条件.OAB结论:空间任意两个向量都是共面向量,所以它们可用
同一平面内的两条有向线段表示。
因此凡是涉及空间任意两个向量的问题,平面向量中有
关结论仍适用于它们。思考:它们确定的平面是否唯一?思考:空间任意两个向量是否可能异面?AB规定零向量与任何向量共线空间向量共线定理:对于空间任意的两个向量,a,b,(a≠0),b与a共线的充要条件是存在实数λ,使b= λ a
相反的向量长度相等且方向
相反的向量长度相等且方向相同 的向量长度相等且方向相同的向量定义表示法向量的模零向量单位向量相反向量相等向量一:空间向量的基本概念ABB零向量的方向是任意的如何理解零向量的方向?例1、给出以下命题:
(1)两个空间向量相等,则它们的起点、终点相同;
(2)若空间向量 满足 ,则 ;
(3)在正方体 中,必有 ;
(4)若空间向量 满足 ,则 ;
(5)空间中任意两个单位向量必相等。
其中不正确命题的个数是———————— (1)(2)(5)变式:如图所示,长方体中
(1)写出与向量 相等的其余向量;
(2) 写出与向量 相反的向量。OAB思考:平面是否唯一?探究一:空间任意两个向量是否都可以平移到同一平面内?为什么?O′结论:空间任意两个向量都可以平移到同一个平面内,
内,成为同一平面内的两个向量。平面向量概念加法
减法
数乘
运算运
算
律定义表示法相等向量减法:三角形法则加法:三角形法则或
平行四边形法则空间向量及其加减与数乘运算空间向量具有大小和方向的量数乘:ka,k为正数,负数,零加法交换律加法结合律数乘分配律OABC探究二:空间向量如何进行加减运算?空间向量的数乘OABC空间向量加法交换律:探究三:空间向量的加法是否满足交换律?b + aa + b
=OABCOABC(空间向量)空间向量的加法是否满足结合律?=加法交换律:加法结合律:空间向量的加法的运算律:数乘分配律平面向量概念加法
减法
数乘
运算运
算
律定义表示法相等向量减法:三角形法则加法:三角形法则或
平行四边形法则空间向量及其加减与数乘运算空间向量具有大小和方向的量数乘:ka,k为正数,负数,零加法交换律加法结合律数乘分配律加法:三角形法则或
平行四边形法则减法:三角形法则数乘:ka,k为正数,负数,零加法结合律 练一练例1:已知平行六面体ABCD-A1B1C1D1,化简下列向量
表达式,并标出化简结果的向量。(如图)GM 始点相同的三个不共面向量之和,等于以这三个向量
为棱的平行六面体的以公共始点为始点的对角线所示向量例2:已知平行六面体ABCD-A1B1C1D1,
求满足下列各式的x的值。例2:已知平行六面体ABCD-A1B1C1D1,
求满足下列各式的x的值。例2:已知平行六面体ABCD-A1B1C1D1,
求满足下列各式的x的值。例2:已知平行六面体ABCD-A1B1C1D1,
求满足下列各式的x的值。ABMCGD(2)原式练习1在空间四边形ABCD中,点M、G分别是BC、CD
边的中点,化简ABCDDCBA练习2E在立方体AC1中,点E是面AC’ 的中心,求下列各式中的x,y.ABCDDCBA练习2E在立方体AC1中,点E是面AC’ 的中心,求下列各式中的x,y.平面向量概念加法
减法
运算运
算
律定义表示法相等向量减法:三角形法则加法:三角形法则或
平行四边形法则空间向量具有大小和方向的量加法交换律加法结合律小结类比、数形结合数乘分配律数乘分配律作业思考题:考虑空间三个向量共面的充要条件.OAB结论:空间任意两个向量都是共面向量,所以它们可用
同一平面内的两条有向线段表示。
因此凡是涉及空间任意两个向量的问题,平面向量中有
关结论仍适用于它们。思考:它们确定的平面是否唯一?思考:空间任意两个向量是否可能异面?AB规定零向量与任何向量共线空间向量共线定理:对于空间任意的两个向量,a,b,(a≠0),b与a共线的充要条件是存在实数λ,使b= λ a
