数学高中苏教版选修(2-2)3.3《复数的几何意义》课件
文档属性
| 名称 | 数学高中苏教版选修(2-2)3.3《复数的几何意义》课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 133.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-07 11:15:33 | ||
图片预览








文档简介
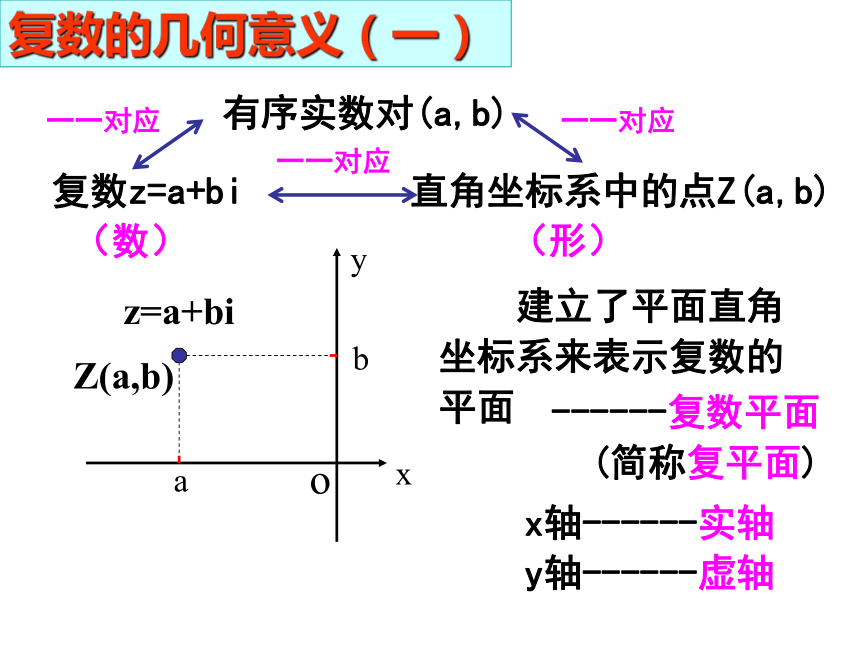
课件33张PPT。3.3 复数的几何意义在几何上,我们用什么来表示实数?想一想?实数的几何意义类比实数的表示,在几何上可以用什么来表示复数?实数可以用数轴上的点来表示。实数 数轴上的点 (形)(数)一一对应 回忆…复数的一般形式?Z=a+bi(a, b∈R)实部!虚部!一个复数由什么确定?复数z=a+bi有序实数对(a,b)直角坐标系中的点Z(a,b)xyobaZ(a,b) 建立了平面直角坐标系来表示复数的平面x轴------实轴y轴------虚轴(数)(形)------复数平面 (简称复平面)一一对应z=a+bi复数的几何意义(一)一一对应一一对应(A)在复平面内,对应于实数的点都在实轴上
(B)在复平面内,对应于纯虚数的点都在虚轴 上;
(C)在复平面内,实轴上的点所对应的复数都是实数;
(D)在复平面内,虚轴上的点所对应的复数都是纯虚数。例1.下列命题中的假命题是( )D2.“a=0”是“复数a+bi(a,b∈R)是纯虚数”的( )
(A)必要不充分条件 (B)充分不必要条件
(C)充要条件 (D)不充分不必要条件C3.“a=0”是“复数a+bi (a,b∈R)所对应的点在虚轴上”的( )
(A)必要不充分条件 (B)充分不必要条件
(C)充要条件 (D)不充分不必要条件A 4.复数z与 所对应的点在复平面内( )
(A)关于x轴对称 (B)关于y轴对称
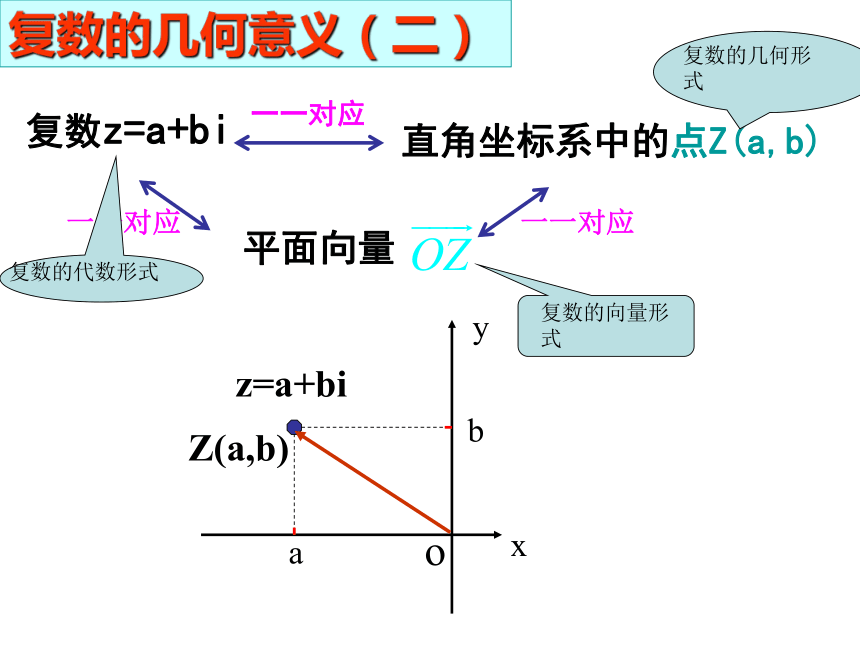
(C)关于原点对称 (D)关于直线y=x对称A例2:已知复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点位于第二象限,求实数m的取值范围。 一种重要的数学思想:数形结合思想变式一:已知复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点在直线x-2y+4=0上,求实数m的值。 解:∵复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点是(m2+m-6,m2+m-2), ∴(m2+m-6)-2(m2+m-2)+4=0, ∴m=1或m=-2复数z=a+bi直角坐标系中的点Z(a,b)一一对应平面向量一一对应一一对应复数的几何意义(二)xyobaZ(a,b)z=a+bixOz=a+biy复数的绝对值(复数的模)的几何意义:Z (a,b)对应平面向量 的模| |,即复数 z=a+bi在复平面上对应的点Z(a,b)到原点的距离。| z | = 思考: | z | 与z, Z有什么关系? 例3:求下列复数的模:
(1)z1=-5i
(2)z2=-3+4i
(3)z3=5-5i (4)z4=1+mi(m∈R)
(5)z5=4a-3ai(a<0)( 5 )( 5 )(-5a )解:实数能比较大小,数系扩充到复数后,Z1,Z2 一般不能比较大小,但复数的模是非负数,可以比较大小。设z=x+yi(x,y∈R)满足|z|=5(z∈C)的复数z对应的点在复平面上将构成怎样的图形?以原点为圆心,5为半径的圆上思考:(1)满足|z|=5(z∈C)的z值有几个?(2)这些复数对应的点在复平面上构成怎样的图形? 5xyO设z=x+yi(x,y∈R)变式:满足3<|z|<5(z∈C)的复数z对应的点在复平面上将构成怎样的图形?55–5–53–3–33以原点为圆心,半径3
至5的圆环内(不含边界)练习:P70,2 P73,4复数z=a+bi直角坐标系中的点Z(a,b)一一对应平面向量一一对应一一对应小结1.| z | 2.作业:P70 1、3复数z=a+bi直角坐标系中的点Z(a,b)一一对应平面向量一一对应一一对应复数的几何意义(二)xyobaZ(a,b)z=a+bixOz=a+biy复数的绝对值(复数的模)的几何意义:Z (a,b)对应平面向量 的模| |,即复数 z=a+bi在复平面上对应的点Z(a,b)到原点的距离。| z | = 思考: | z | 与z, Z有什么关系? 例3:求下列复数的模:
(1)z1=-5i
(2)z2=-3+4i
(3)z3=5-5i (4)z4=1+mi(m∈R)
(5)z5=4a-3ai(a<0)( 5 )( 5 )(-5a )复数的模是非负数解:实数能比较大小,数系扩充到复数后,Z1,Z2 一般不能比较大小,但复数的模是非负数,可以比较大小。设z=x+yi(x,y∈R)满足|z|=5(z∈C)的复数z对应的点在复平面上将构成怎样的图形?以原点为圆心,5为半径的圆上思考:(1)满足|z|=5(z∈C)的z值有几个?(2)这些复数对应的点在复平面上构成怎样的图形? 5xyO设z=x+yi(x,y∈R)变式:满足3<|z|<5(z∈C)的复数z对应的点在复平面上将构成怎样的图形?55–5–53–3–33以原点为圆心,半径3
至5的圆环内(不含边界)练习:P70,2 P73,4xoyZ1(a,b)Z2(c,d)Z(a+c,b+d)z1+ z2=OZ1 +OZ2 = OZ符合向量加法的平行四边形法则.1.复数加法运算的几何意义?新课讲解xoy符合向量减法的三角形法则.2.复数减法运算的几何意义?|z1-z2|表示什么?表示复平面上两点Z1 ,Z2的距离复数z1-z2 =(a-c)+( b-d) iZ2Z1(1)|z-(1+2i)|(2)|z+(1+2i)|已知复数z对应点A,说明下列各式所表示的几何意义.点A到点(1,2)的距离点A到点(-1, -2)的距离(3)|z-1|(4)|z+2i|点A到点(1,0)的距离点A到点(0, -2)的距离练习:已知复数m=2-3i,若复数z满足不等式|z-m|=1,则z所对应的点的集合是什么图形?以点(2, -3)为圆心,
1为半径的圆上复数减法的几何意义的运用设复数z=x+yi,(x,y∈R),在下列条件下
求动点Z(x,y)的轨迹.
| z- 2|= 1
2.| z- i|+ | z+ i|=4
3.| z- 2|= | z+ 4|xyoZ2ZZZ当| z- z1|=r时, 复数z对应的点的轨迹是以
Z1对应的点为圆心,半径为r的圆.1-1ZZZyxo|z-z1|+|z-z2|=2a|z1-z2|<2a|z2-z1|=2a|z2-z1|>2a椭圆线段无轨迹yxo2-4 x=-1当| z- z1|= | z- z2|时, 复数z对应的点的轨迹是
线段Z1Z2的中垂线.-1练习:
P69,4,5
P70,4,5
P73,71、|z1|= |z2|
平行四边形OABC是2、| z1+ z2|= | z1- z2|
平行四边形OABC是3、 |z1|= |z2|,| z1+ z2|= | z1- z2|
平行四边形OABC是oz2-z1ABC菱形矩形正方形三、复数加减法的几何意义三、复数加减法的几何意义的运用练习1:设z1,z2∈C, |z1|= |z2|=1
|z2+z1|= 求|z2-z1| 练习2:复数z1,z2分别对应复平面内的点M1,M2,,且| z2+ z1|= | z2- z1|,线段M1M2,的中点M对应的复数为4+3i,求|z1|2+ |z2|2 100
(B)在复平面内,对应于纯虚数的点都在虚轴 上;
(C)在复平面内,实轴上的点所对应的复数都是实数;
(D)在复平面内,虚轴上的点所对应的复数都是纯虚数。例1.下列命题中的假命题是( )D2.“a=0”是“复数a+bi(a,b∈R)是纯虚数”的( )
(A)必要不充分条件 (B)充分不必要条件
(C)充要条件 (D)不充分不必要条件C3.“a=0”是“复数a+bi (a,b∈R)所对应的点在虚轴上”的( )
(A)必要不充分条件 (B)充分不必要条件
(C)充要条件 (D)不充分不必要条件A 4.复数z与 所对应的点在复平面内( )
(A)关于x轴对称 (B)关于y轴对称
(C)关于原点对称 (D)关于直线y=x对称A例2:已知复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点位于第二象限,求实数m的取值范围。 一种重要的数学思想:数形结合思想变式一:已知复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点在直线x-2y+4=0上,求实数m的值。 解:∵复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点是(m2+m-6,m2+m-2), ∴(m2+m-6)-2(m2+m-2)+4=0, ∴m=1或m=-2复数z=a+bi直角坐标系中的点Z(a,b)一一对应平面向量一一对应一一对应复数的几何意义(二)xyobaZ(a,b)z=a+bixOz=a+biy复数的绝对值(复数的模)的几何意义:Z (a,b)对应平面向量 的模| |,即复数 z=a+bi在复平面上对应的点Z(a,b)到原点的距离。| z | = 思考: | z | 与z, Z有什么关系? 例3:求下列复数的模:
(1)z1=-5i
(2)z2=-3+4i
(3)z3=5-5i (4)z4=1+mi(m∈R)
(5)z5=4a-3ai(a<0)( 5 )( 5 )(-5a )解:实数能比较大小,数系扩充到复数后,Z1,Z2 一般不能比较大小,但复数的模是非负数,可以比较大小。设z=x+yi(x,y∈R)满足|z|=5(z∈C)的复数z对应的点在复平面上将构成怎样的图形?以原点为圆心,5为半径的圆上思考:(1)满足|z|=5(z∈C)的z值有几个?(2)这些复数对应的点在复平面上构成怎样的图形? 5xyO设z=x+yi(x,y∈R)变式:满足3<|z|<5(z∈C)的复数z对应的点在复平面上将构成怎样的图形?55–5–53–3–33以原点为圆心,半径3
至5的圆环内(不含边界)练习:P70,2 P73,4复数z=a+bi直角坐标系中的点Z(a,b)一一对应平面向量一一对应一一对应小结1.| z | 2.作业:P70 1、3复数z=a+bi直角坐标系中的点Z(a,b)一一对应平面向量一一对应一一对应复数的几何意义(二)xyobaZ(a,b)z=a+bixOz=a+biy复数的绝对值(复数的模)的几何意义:Z (a,b)对应平面向量 的模| |,即复数 z=a+bi在复平面上对应的点Z(a,b)到原点的距离。| z | = 思考: | z | 与z, Z有什么关系? 例3:求下列复数的模:
(1)z1=-5i
(2)z2=-3+4i
(3)z3=5-5i (4)z4=1+mi(m∈R)
(5)z5=4a-3ai(a<0)( 5 )( 5 )(-5a )复数的模是非负数解:实数能比较大小,数系扩充到复数后,Z1,Z2 一般不能比较大小,但复数的模是非负数,可以比较大小。设z=x+yi(x,y∈R)满足|z|=5(z∈C)的复数z对应的点在复平面上将构成怎样的图形?以原点为圆心,5为半径的圆上思考:(1)满足|z|=5(z∈C)的z值有几个?(2)这些复数对应的点在复平面上构成怎样的图形? 5xyO设z=x+yi(x,y∈R)变式:满足3<|z|<5(z∈C)的复数z对应的点在复平面上将构成怎样的图形?55–5–53–3–33以原点为圆心,半径3
至5的圆环内(不含边界)练习:P70,2 P73,4xoyZ1(a,b)Z2(c,d)Z(a+c,b+d)z1+ z2=OZ1 +OZ2 = OZ符合向量加法的平行四边形法则.1.复数加法运算的几何意义?新课讲解xoy符合向量减法的三角形法则.2.复数减法运算的几何意义?|z1-z2|表示什么?表示复平面上两点Z1 ,Z2的距离复数z1-z2 =(a-c)+( b-d) iZ2Z1(1)|z-(1+2i)|(2)|z+(1+2i)|已知复数z对应点A,说明下列各式所表示的几何意义.点A到点(1,2)的距离点A到点(-1, -2)的距离(3)|z-1|(4)|z+2i|点A到点(1,0)的距离点A到点(0, -2)的距离练习:已知复数m=2-3i,若复数z满足不等式|z-m|=1,则z所对应的点的集合是什么图形?以点(2, -3)为圆心,
1为半径的圆上复数减法的几何意义的运用设复数z=x+yi,(x,y∈R),在下列条件下
求动点Z(x,y)的轨迹.
| z- 2|= 1
2.| z- i|+ | z+ i|=4
3.| z- 2|= | z+ 4|xyoZ2ZZZ当| z- z1|=r时, 复数z对应的点的轨迹是以
Z1对应的点为圆心,半径为r的圆.1-1ZZZyxo|z-z1|+|z-z2|=2a|z1-z2|<2a|z2-z1|=2a|z2-z1|>2a椭圆线段无轨迹yxo2-4 x=-1当| z- z1|= | z- z2|时, 复数z对应的点的轨迹是
线段Z1Z2的中垂线.-1练习:
P69,4,5
P70,4,5
P73,71、|z1|= |z2|
平行四边形OABC是2、| z1+ z2|= | z1- z2|
平行四边形OABC是3、 |z1|= |z2|,| z1+ z2|= | z1- z2|
平行四边形OABC是oz2-z1ABC菱形矩形正方形三、复数加减法的几何意义三、复数加减法的几何意义的运用练习1:设z1,z2∈C, |z1|= |z2|=1
|z2+z1|= 求|z2-z1| 练习2:复数z1,z2分别对应复平面内的点M1,M2,,且| z2+ z1|= | z2- z1|,线段M1M2,的中点M对应的复数为4+3i,求|z1|2+ |z2|2 100
