数学高中苏教版选修(2-3)2.5《离散型随机变量的均值与方差》课件3
文档属性
| 名称 | 数学高中苏教版选修(2-3)2.5《离散型随机变量的均值与方差》课件3 |

|
|
| 格式 | zip | ||
| 文件大小 | 99.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-07 00:00:00 | ||
图片预览








文档简介
课件28张PPT。※2.5.1离散型随机变量的均值1高二数学 选修2-3学习目标:
1)理解取有限值的离散型随机变量的均值、方差、标准差的概念和意义;
2)能计算简单的离散型随机变量的均值、方差、标准差,解决一些实际问题;1、什么叫n次独立重复试验? 一般地,由n次试验构成,且每次试验互相独立完成,每次试验的结果仅有两种对立的状态,即A与 ,每次试验中P(A)=p>0。称这样的试验为n次独立重复试验,也称伯努利试验。n次独立重复试验的特征为: 1)每次试验是在同样的条件下进行的;
2)各次试验中的事件是相互独立的;
3)每次试验都只有两种结果:发生与不发生;
4)每次试验,某事件发生的概率是相同的.2、什么叫二项分布?复习回顾一般地,设离散型随机变量ξ可能取的值为 x1,x2,……,xi,…, ξ取每一个值xi(i=1,2,…)的概率P(ξ=xi)=pi,则称下表为随机变量ξ的概率分布.由概率的性质可知,任一离散型随机变量的分布都具有下述两个性质:
3、离散型随机变量的概率分布(1)pi≥0,i=1,2,…,n
(2)p1+p2+…+pi+…+pn=1复习引入 对于离散型随机变量,可以由它的概率分布确定与该随机变量相关事件的概率.但在实际问题中,有时我们更感兴趣的是随机变量的某些数字特征.例如:要了解某班同学在一次数学测验中的总体水平,很重要的是看平均分;要了解某班同学数学成绩是否“两极分化”则需要考察这个班数学成绩的方差。
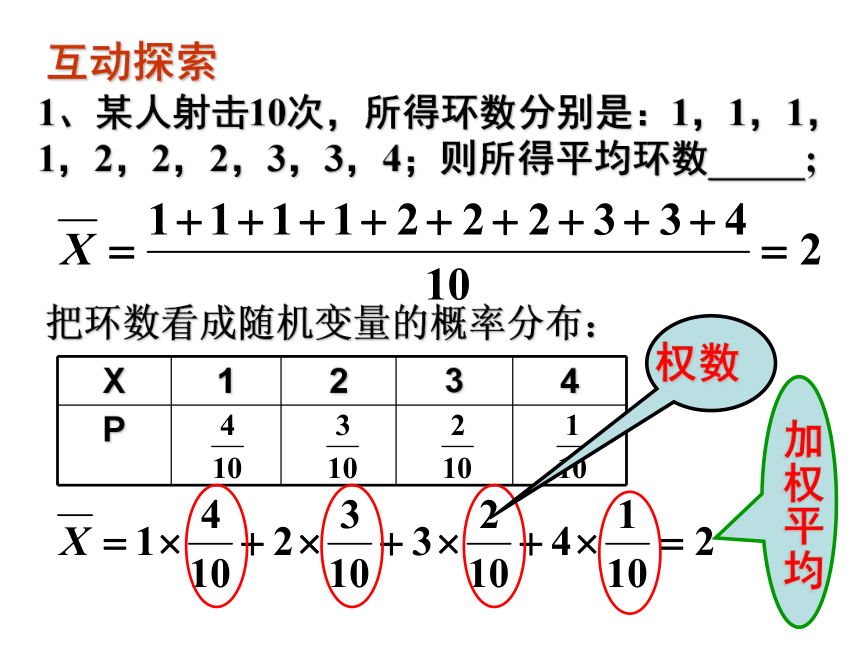
我们还常常希望直接通过数字来反映随机变量的某个方面的特征,最常用的有期望与方差。1、某人射击10次,所得环数分别是:1,1,1,1,2,2,2,3,3,4;则所得平均环数_____;把环数看成随机变量的概率分布:权数加权平均互动探索2、某商场要将单价分别为18元/kg,24元/kg,36元/kg的3种糖果按3:2:1的比例混合销售,如何对混合糖果定价才合理?把3种糖果的价格看成随机变量的概率分布列:互动探索1.离散型随机变量取值的平均值(数学期望)一般地,若离散型随机变量X的概率分布为:则称为随机变量X的均值或数学期望,它反映了离散型随机变量取值的平均水平.意义建构设Y=aX+b,其中a,b为常数,则Y也是随机变量.
(1) Y的分布是什么?
(2) EY=?思考:意义建构······························意义建构 的分布列为结论1: 则意义建构3.基础训练1)随机变量ξ的分布列是(1)则Eξ=____________; 2)随机变量ξ的分布列是2.4(2)若η=2ξ+1,则Eη=____________; 5.8Eξ=7.5,则a=______,b= ________;0.40.1例1.篮球运动员在比赛中每次罚球命中得1分,罚不中得0分.已知某运动员罚球命中的概率
为0.7,求他罚球1次的得分X的均值。一般地,如果随机变量X服从两点分布,则4.例题讲解提炼结论:例2.篮球运动员在比赛中每次罚球命中得1分,罚不中得0分.已知某运动员罚球命中的概率为0.7,他连续罚球3次;
(1)求他得到的分数X的概率分布;
(2)求X的数学期望。解:(1) X~B(3,0.7)(2)4.例题讲解一般地,如果随机变量X服从二项分布,即X~B(n , p),则提炼结论2:基础训练:一个袋子里装有大小相同的3 个红球和2个黄球,从中有放回地取5次,则取到红球次数的数学期望是 .31)一次英语单元测验由20个选择题构成,每个选择题有4个选项,其中有且只有一个选项是正确答案,每题选择正确答案得5分,不作出选择或选错不得分,满分100分,学生甲选对任一题的概率为0.9,学生乙则在测验中对每题都从4个选项中随机地选择一个。求学生甲和乙在这次英语单元测验中的成绩的期望。5.巩固应用不一定,其含义是在多次类似的测试中,他的平均成绩大约是90分解:设学生甲和学生乙在这次测验中选择正确的选择题个数分别是ξ和η,则 ξ~B(20,0.9),η~B(20,0.25),所以Eξ=20×0.9=18,Eη=20×0.25=5.由于答对每题得5分,学生甲和学生乙在这次测验中的成绩分别是5ξ和5η.这样,他们在测验中的成绩的期望分别是E(5ξ)=5Eξ=5×18=90,E(5η)=5Eη=5×5=25.思考:学生甲在这次测试中的成绩一定会是90分吗?他的均值为90分的含义是什么?5.巩固应用2)某商场的促销决策:
统计资料表明,每年国庆节商场内促销活动可获利2万元;商场外促销活动如不遇下雨可获利10万元;如遇下雨则损失4万元。9月30日气象预报国庆节下雨的概率为40%,问: 商场应选择哪种促销方式?巩固应用3.有一批数量很大的产品,其次品率是15%,对这批产品进行抽查,每次抽出1件,如果抽出次品,则抽查终止,否则继续抽查,直到抽出次品,但抽查次数最多不超过10次.求抽查次数ξ的期望(结果保留三个有效数字).分析(1)P(ξ=k)=0.85 k-1×0.15,( k=1,2,…,9) k=10时,前9次取出的都是正品,第10次可能取出次品,也可能取出正品,
所以P(ξ=10)=0.859×(0.15+0.85)=0.859(2)写出ξ的分布列,由概率分布可得可得 的期望E = 1000-0.03a≥0.07a得a≤10000故最大定为10000元。强化巩固练习:
1、每人交保险费1000元,出险概率为3%,若保险公司的赔偿金为a(a>1000)元,为使保险公司收益的期望值不低于a的百分之七,求保险公司应将最大赔偿金定为多少元?2、射手用手枪进行射击,击中目标就停止,否则继续射击,他射中目标的概率是0.7,若枪内只有5颗子弹,求射击次数的期望。(保留三个有效数字)E =1.436.课堂小结1)离散型随机变量取值的平均值数学期望2)数学期望的性质3)若随机变量X服从两点分布则4)若随机变量X服从二项分布,
即X~B(n,p),则5)若随机变量X服从超几何分布,
即X~H(n,M,N),则∴E ξ =0×Cn0p0qn+ 1×Cn1p1qn-1+ 2×Cn2p2qn-2 +
…+ k×Cnkpkqn-k+…+ n×Cnnpnq0∵P(ξ=k)= Cnkpkqn-k证明:=np(Cn-10p0qn-1+ Cn-11p1qn-2+ … +
Cn-1k-1pk-1q(n-1)-(k-1) +…+ Cn-1n-1pn-1q0)
=np(p+q)n-1=np(∵ k Cnk =n Cn-1k-1)证明结论:若ξ~B(n,p),则Eξ= np所以 若ξ~B(n,p),则Eξ=np. 应用思考1:
有场赌博,规则如下:投掷一个质地均匀骰子,向上的点数出现1,你可赢得10元;出现2或3或4,你输3元;出现5或6,不输不赢.问这场赌博对你是否有利?
若改为8元呢?
应用思考2:
彩球游戏准备一个布袋,内装6个红球与6个白球,
除颜色不同外,12个球完全一样,每次从袋中摸6个球,输赢的规则为: ①6个全红 赢得100元
②5红1白 赢得50元
③4红2白 赢得20元
④3红3白 输100元
⑤2红4白 赢得20元
⑥1红5白 赢得50元
⑦6个全白 赢得100元你心动了吗? 祝学习进步!
1)理解取有限值的离散型随机变量的均值、方差、标准差的概念和意义;
2)能计算简单的离散型随机变量的均值、方差、标准差,解决一些实际问题;1、什么叫n次独立重复试验? 一般地,由n次试验构成,且每次试验互相独立完成,每次试验的结果仅有两种对立的状态,即A与 ,每次试验中P(A)=p>0。称这样的试验为n次独立重复试验,也称伯努利试验。n次独立重复试验的特征为: 1)每次试验是在同样的条件下进行的;
2)各次试验中的事件是相互独立的;
3)每次试验都只有两种结果:发生与不发生;
4)每次试验,某事件发生的概率是相同的.2、什么叫二项分布?复习回顾一般地,设离散型随机变量ξ可能取的值为 x1,x2,……,xi,…, ξ取每一个值xi(i=1,2,…)的概率P(ξ=xi)=pi,则称下表为随机变量ξ的概率分布.由概率的性质可知,任一离散型随机变量的分布都具有下述两个性质:
3、离散型随机变量的概率分布(1)pi≥0,i=1,2,…,n
(2)p1+p2+…+pi+…+pn=1复习引入 对于离散型随机变量,可以由它的概率分布确定与该随机变量相关事件的概率.但在实际问题中,有时我们更感兴趣的是随机变量的某些数字特征.例如:要了解某班同学在一次数学测验中的总体水平,很重要的是看平均分;要了解某班同学数学成绩是否“两极分化”则需要考察这个班数学成绩的方差。
我们还常常希望直接通过数字来反映随机变量的某个方面的特征,最常用的有期望与方差。1、某人射击10次,所得环数分别是:1,1,1,1,2,2,2,3,3,4;则所得平均环数_____;把环数看成随机变量的概率分布:权数加权平均互动探索2、某商场要将单价分别为18元/kg,24元/kg,36元/kg的3种糖果按3:2:1的比例混合销售,如何对混合糖果定价才合理?把3种糖果的价格看成随机变量的概率分布列:互动探索1.离散型随机变量取值的平均值(数学期望)一般地,若离散型随机变量X的概率分布为:则称为随机变量X的均值或数学期望,它反映了离散型随机变量取值的平均水平.意义建构设Y=aX+b,其中a,b为常数,则Y也是随机变量.
(1) Y的分布是什么?
(2) EY=?思考:意义建构······························意义建构 的分布列为结论1: 则意义建构3.基础训练1)随机变量ξ的分布列是(1)则Eξ=____________; 2)随机变量ξ的分布列是2.4(2)若η=2ξ+1,则Eη=____________; 5.8Eξ=7.5,则a=______,b= ________;0.40.1例1.篮球运动员在比赛中每次罚球命中得1分,罚不中得0分.已知某运动员罚球命中的概率
为0.7,求他罚球1次的得分X的均值。一般地,如果随机变量X服从两点分布,则4.例题讲解提炼结论:例2.篮球运动员在比赛中每次罚球命中得1分,罚不中得0分.已知某运动员罚球命中的概率为0.7,他连续罚球3次;
(1)求他得到的分数X的概率分布;
(2)求X的数学期望。解:(1) X~B(3,0.7)(2)4.例题讲解一般地,如果随机变量X服从二项分布,即X~B(n , p),则提炼结论2:基础训练:一个袋子里装有大小相同的3 个红球和2个黄球,从中有放回地取5次,则取到红球次数的数学期望是 .31)一次英语单元测验由20个选择题构成,每个选择题有4个选项,其中有且只有一个选项是正确答案,每题选择正确答案得5分,不作出选择或选错不得分,满分100分,学生甲选对任一题的概率为0.9,学生乙则在测验中对每题都从4个选项中随机地选择一个。求学生甲和乙在这次英语单元测验中的成绩的期望。5.巩固应用不一定,其含义是在多次类似的测试中,他的平均成绩大约是90分解:设学生甲和学生乙在这次测验中选择正确的选择题个数分别是ξ和η,则 ξ~B(20,0.9),η~B(20,0.25),所以Eξ=20×0.9=18,Eη=20×0.25=5.由于答对每题得5分,学生甲和学生乙在这次测验中的成绩分别是5ξ和5η.这样,他们在测验中的成绩的期望分别是E(5ξ)=5Eξ=5×18=90,E(5η)=5Eη=5×5=25.思考:学生甲在这次测试中的成绩一定会是90分吗?他的均值为90分的含义是什么?5.巩固应用2)某商场的促销决策:
统计资料表明,每年国庆节商场内促销活动可获利2万元;商场外促销活动如不遇下雨可获利10万元;如遇下雨则损失4万元。9月30日气象预报国庆节下雨的概率为40%,问: 商场应选择哪种促销方式?巩固应用3.有一批数量很大的产品,其次品率是15%,对这批产品进行抽查,每次抽出1件,如果抽出次品,则抽查终止,否则继续抽查,直到抽出次品,但抽查次数最多不超过10次.求抽查次数ξ的期望(结果保留三个有效数字).分析(1)P(ξ=k)=0.85 k-1×0.15,( k=1,2,…,9) k=10时,前9次取出的都是正品,第10次可能取出次品,也可能取出正品,
所以P(ξ=10)=0.859×(0.15+0.85)=0.859(2)写出ξ的分布列,由概率分布可得可得 的期望E = 1000-0.03a≥0.07a得a≤10000故最大定为10000元。强化巩固练习:
1、每人交保险费1000元,出险概率为3%,若保险公司的赔偿金为a(a>1000)元,为使保险公司收益的期望值不低于a的百分之七,求保险公司应将最大赔偿金定为多少元?2、射手用手枪进行射击,击中目标就停止,否则继续射击,他射中目标的概率是0.7,若枪内只有5颗子弹,求射击次数的期望。(保留三个有效数字)E =1.436.课堂小结1)离散型随机变量取值的平均值数学期望2)数学期望的性质3)若随机变量X服从两点分布则4)若随机变量X服从二项分布,
即X~B(n,p),则5)若随机变量X服从超几何分布,
即X~H(n,M,N),则∴E ξ =0×Cn0p0qn+ 1×Cn1p1qn-1+ 2×Cn2p2qn-2 +
…+ k×Cnkpkqn-k+…+ n×Cnnpnq0∵P(ξ=k)= Cnkpkqn-k证明:=np(Cn-10p0qn-1+ Cn-11p1qn-2+ … +
Cn-1k-1pk-1q(n-1)-(k-1) +…+ Cn-1n-1pn-1q0)
=np(p+q)n-1=np(∵ k Cnk =n Cn-1k-1)证明结论:若ξ~B(n,p),则Eξ= np所以 若ξ~B(n,p),则Eξ=np. 应用思考1:
有场赌博,规则如下:投掷一个质地均匀骰子,向上的点数出现1,你可赢得10元;出现2或3或4,你输3元;出现5或6,不输不赢.问这场赌博对你是否有利?
若改为8元呢?
应用思考2:
彩球游戏准备一个布袋,内装6个红球与6个白球,
除颜色不同外,12个球完全一样,每次从袋中摸6个球,输赢的规则为: ①6个全红 赢得100元
②5红1白 赢得50元
③4红2白 赢得20元
④3红3白 输100元
⑤2红4白 赢得20元
⑥1红5白 赢得50元
⑦6个全白 赢得100元你心动了吗? 祝学习进步!
