北师大版九年级下册 1.4 解直角三角形 课件(共15张PPT)
文档属性
| 名称 | 北师大版九年级下册 1.4 解直角三角形 课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-16 23:49:18 | ||
图片预览






文档简介
(共15张PPT)
1.4 解直角三角形
教学目标:
1.知道解直角三角形的概念、理解直角三角形中五个元素的关系。
2.通过综合运用勾股定理,掌握解直角三角形,逐步形成分析问题、解决问题的能力.
3.渗透数形结合的数学思想,养成良好的学习习惯.
教学重点及难点:
教学重点:掌握利用直角三角形边角关系解直角三角形
教学难点:锐角三角比在解直角三角形中的灵活运用
教师提问:
1、直角三角形边的关系
2、直角三角形锐角的关系
3、直角三角形边角关系
交流预习
随堂练习
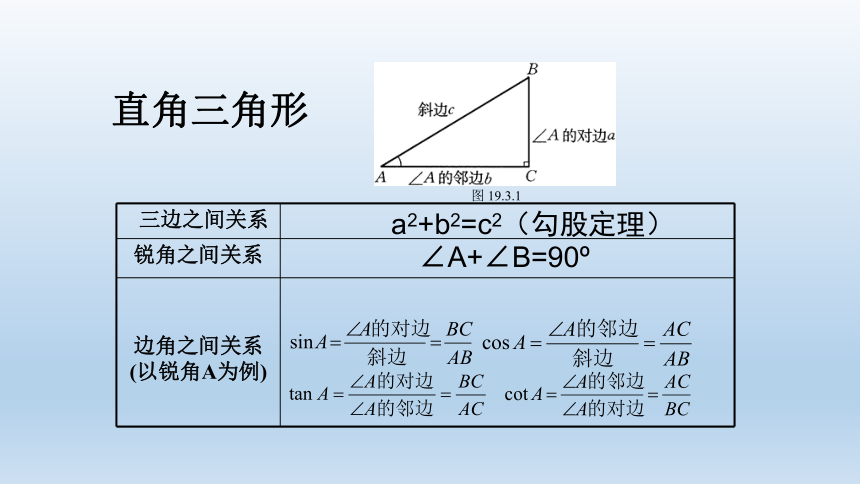
直角三角形
三边之间关系
锐角之间关系
边角之间关系 (以锐角A为例)
a2+b2=c2(勾股定理)
∠A+∠B=90
在Rt△ABC中,∠C=90°,AC=12,
AB=13,则有
①根据勾股定理得:
BC=_________=______
②sinA =_____=_____
③cosA =_______ = _______
④tanA =_____=____⑤ cotA = ___ = ___
5
132-122
12
13
5
互助探究
教师讲解:
例1 如图,在Rt△ABC中,∠C=90°,
解这个直角三角形
解:
A
B
C
事实上,在直角三角形的六个元素中,除直角外,如果再知道两个元素(其中至少有一个是边),这个三角形就可以确定下来,这样就可以由已知的两个元素求出其余的三个元素.
A
B
a
b
c
C
解直角三角形:在直角三角形中,由已知元素求未知元素的过程.
在解直角三角形的过程中,一般要用到下面一些关系:
解直角三角形
(2)两锐角之间的关系
∠A+∠B=90°
(3)边角之间的关系
(1)三边之间的关系
(勾股定理)
A
B
a
b
c
C
在解直角三角形的过程中,一般要用到下面一些关系:
师友训练:
例1. 如图所示,一棵大树在一次强烈的地震中于离地面10米处折断倒下,树顶落在离树根24米处.大树在折断之前高多少?
解 利用勾股定理可以求出折断倒下部分的长度为:
26+10=36(米).
答:大树在折断之前高为36米.
分层提高
教师提升:
在图中的Rt△ABC中,
(1)根据∠A=75°,斜边AB=6,你能求出这个直角三角形的其他元素吗?
A
B
C
α
能
6
=75°
师友归纳:
请你对本节课的学习总结评价
教师总结:
(1)画示意图;
(2)分析已知量与待求量的关系,选择适当的边角关系;
(3)求解;
“有斜(斜边)用弦(正弦、余弦),无斜(斜边)用切(正切)”
“宁乘勿除,取原(原始数据)避中(中间数据)”
巩固反馈
在电线杆离地面8米高的地方向地面拉一条长10米的缆绳,问这条缆绳应固定在距离电线杆底部多远的地方?
B
C
A
巩固反馈
例题: 如图,在Rt△ABC中,∠C=90°,AC=6, ∠BAC的平分线 ,解这个直角三角形.
D
A
B
C
6
解:
因为AD平分∠BAC
教师评价:
解直角三角形,只有下面两种情况:
(1)已知两条边;
(2)已知一条边和一个锐角.
定义:在直角三角形中,由已 知元素求出未知元素的过程,叫做解直角三角形;
在解决实际问题时,应“先画图,再求解”;
1.4 解直角三角形
教学目标:
1.知道解直角三角形的概念、理解直角三角形中五个元素的关系。
2.通过综合运用勾股定理,掌握解直角三角形,逐步形成分析问题、解决问题的能力.
3.渗透数形结合的数学思想,养成良好的学习习惯.
教学重点及难点:
教学重点:掌握利用直角三角形边角关系解直角三角形
教学难点:锐角三角比在解直角三角形中的灵活运用
教师提问:
1、直角三角形边的关系
2、直角三角形锐角的关系
3、直角三角形边角关系
交流预习
随堂练习
直角三角形
三边之间关系
锐角之间关系
边角之间关系 (以锐角A为例)
a2+b2=c2(勾股定理)
∠A+∠B=90
在Rt△ABC中,∠C=90°,AC=12,
AB=13,则有
①根据勾股定理得:
BC=_________=______
②sinA =_____=_____
③cosA =_______ = _______
④tanA =_____=____⑤ cotA = ___ = ___
5
132-122
12
13
5
互助探究
教师讲解:
例1 如图,在Rt△ABC中,∠C=90°,
解这个直角三角形
解:
A
B
C
事实上,在直角三角形的六个元素中,除直角外,如果再知道两个元素(其中至少有一个是边),这个三角形就可以确定下来,这样就可以由已知的两个元素求出其余的三个元素.
A
B
a
b
c
C
解直角三角形:在直角三角形中,由已知元素求未知元素的过程.
在解直角三角形的过程中,一般要用到下面一些关系:
解直角三角形
(2)两锐角之间的关系
∠A+∠B=90°
(3)边角之间的关系
(1)三边之间的关系
(勾股定理)
A
B
a
b
c
C
在解直角三角形的过程中,一般要用到下面一些关系:
师友训练:
例1. 如图所示,一棵大树在一次强烈的地震中于离地面10米处折断倒下,树顶落在离树根24米处.大树在折断之前高多少?
解 利用勾股定理可以求出折断倒下部分的长度为:
26+10=36(米).
答:大树在折断之前高为36米.
分层提高
教师提升:
在图中的Rt△ABC中,
(1)根据∠A=75°,斜边AB=6,你能求出这个直角三角形的其他元素吗?
A
B
C
α
能
6
=75°
师友归纳:
请你对本节课的学习总结评价
教师总结:
(1)画示意图;
(2)分析已知量与待求量的关系,选择适当的边角关系;
(3)求解;
“有斜(斜边)用弦(正弦、余弦),无斜(斜边)用切(正切)”
“宁乘勿除,取原(原始数据)避中(中间数据)”
巩固反馈
在电线杆离地面8米高的地方向地面拉一条长10米的缆绳,问这条缆绳应固定在距离电线杆底部多远的地方?
B
C
A
巩固反馈
例题: 如图,在Rt△ABC中,∠C=90°,AC=6, ∠BAC的平分线 ,解这个直角三角形.
D
A
B
C
6
解:
因为AD平分∠BAC
教师评价:
解直角三角形,只有下面两种情况:
(1)已知两条边;
(2)已知一条边和一个锐角.
定义:在直角三角形中,由已 知元素求出未知元素的过程,叫做解直角三角形;
在解决实际问题时,应“先画图,再求解”;
