北师大版数学九年级下册 3.4圆周角和圆心角的关系-课件(共30张PPT)
文档属性
| 名称 | 北师大版数学九年级下册 3.4圆周角和圆心角的关系-课件(共30张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 907.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-17 00:00:00 | ||
图片预览





文档简介
(共30张PPT)
第三章 圆
第4节 圆周角与圆心角之间的关系第一课时
O
1.圆心角的定义
.
B
C
答:在同圆或等圆中,相等的圆心角所对的弧也相等。
答:顶点在圆心的角叫圆心角.
2.圆心角和它所对的弧的关系
引入新课
2017年3月23日晚,国足在俄罗斯世预赛12强赛第六轮的比赛中以1-0打赢韩国,请大家观看视频
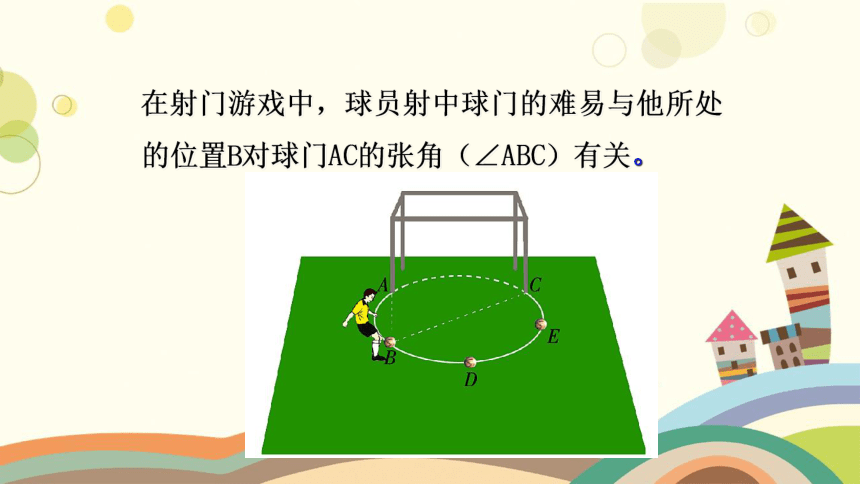
在射门游戏中,球员射中球门的难易与他所处的位置B对球门AC的张角(∠ABC)有关。
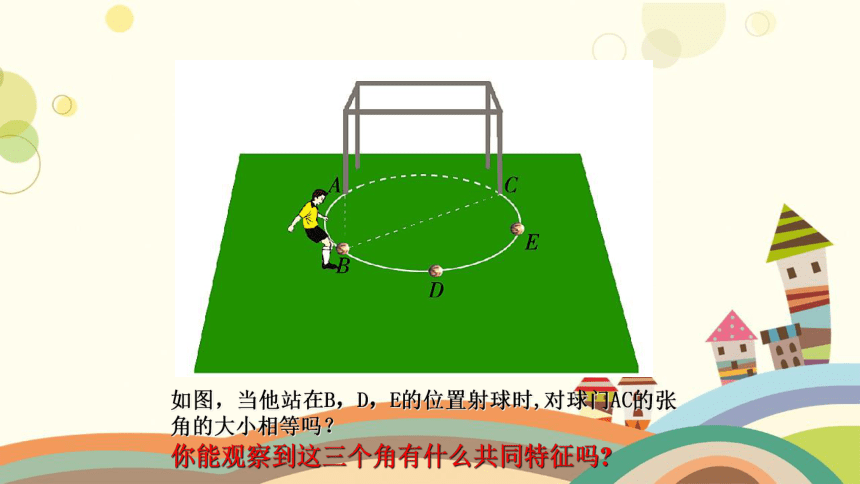
如图,当他站在B,D,E的位置射球时,对球门AC的张角的大小相等吗?
你能观察到这三个角有什么共同特征吗
你能仿照圆心角的定义给圆周角下定义吗
.
O
B
C
A
特征:
①角的顶点在圆上.
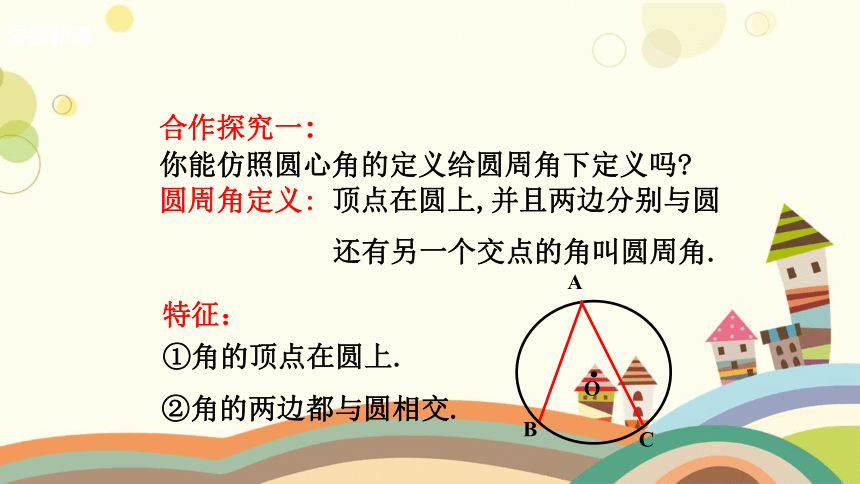
圆周角定义: 顶点在圆上,并且两边分别与圆
还有另一个交点的角叫圆周角.
②角的两边都与圆相交.
合作探究一:
讲授新课
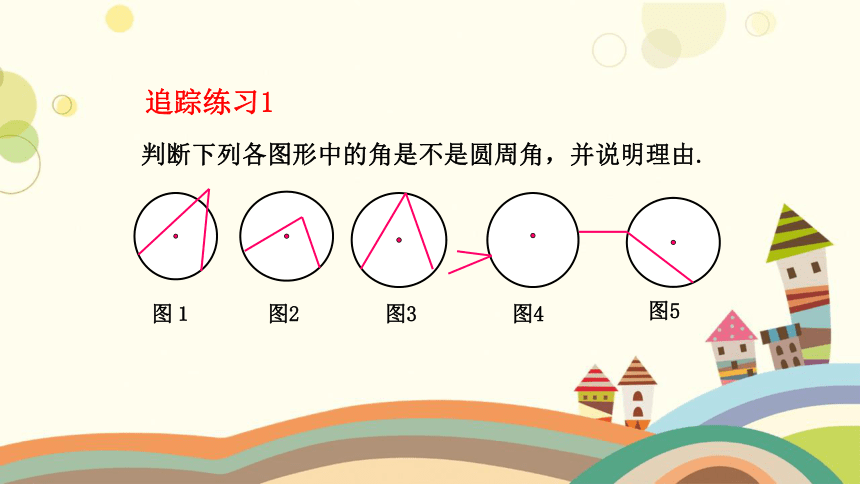
判断下列各图形中的角是不是圆周角,并说明理由.
图1
图2
图3
图4
图5
追踪练习1
圆周角的性质
我们先研究一条弧所对的圆周角与它所对的圆心角之间的关系。
请同学们在圆上确定一条劣弧,画出它所对的圆心角与圆周角。
A
C
合作探究2
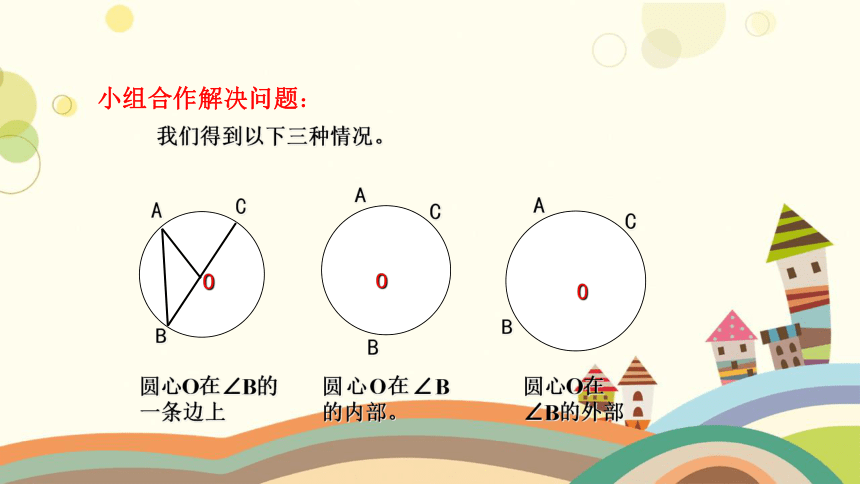
小组合作解决问题:
我们得到以下三种情况。
B
A
O
C
圆心O在∠B的一条边上
A
B
C
O
圆心O在∠B的内部。
B
A
C
O
圆心O在∠B的外部
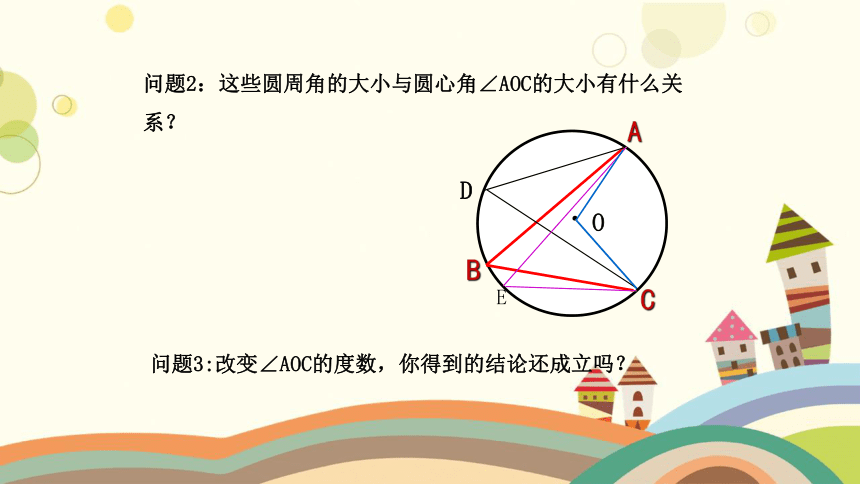
问题2:这些圆周角的大小与圆心角∠AOC的大小有什么关系?
问题3:改变∠AOC的度数,你得到的结论还成立吗?
A
B
C
E
·
O
D
结论:(1)圆周角的度数等于它所对弧上圆心角度 数的一半.
(2)同弧或等弧所对的圆周角相等
圆周角和圆心角的关系
●O
A
B
C
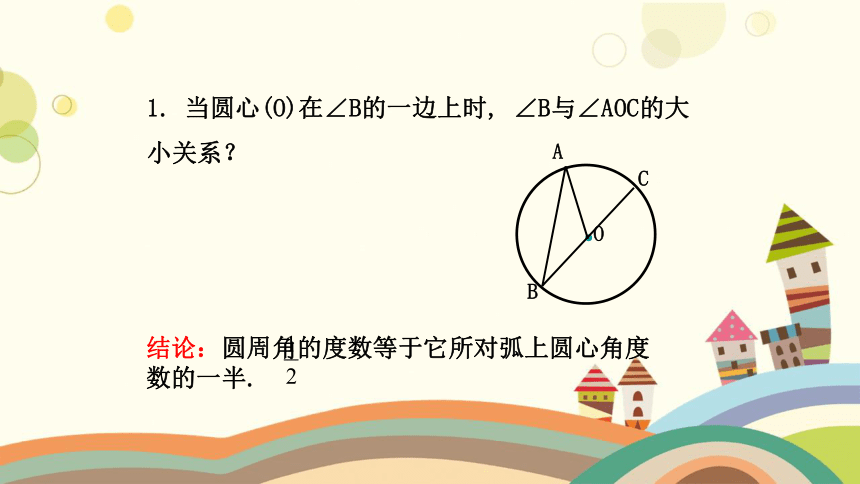
结论:圆周角的度数等于它所对弧上圆心角度 数的一半.
1. 当圆心(O)在∠B的一边上时, ∠B与∠AOC的大小关系?
提示:能否转化为1的情况
结论:一条弧所对的圆周角等于它所对的圆心角的一半.
●O
A
B
C
2.当圆心O在圆周角∠B的内部时,∠B与∠AOC的大小关系
结论:圆周角的度数等于它所对弧上圆心角度数的一半.
D
●O
A
B
C
3.当圆心O在∠B的外部时,∠B与∠AOC的大小关系
圆周角定理:
圆周角的度数等于它所对弧上圆心角度数的一半.
B
A
O
C
圆心O在∠B的一条边上
A
B
C
O
圆心O在∠B的内部。
B
A
C
O
圆心O在∠B的外部
图形语言:
几何语言:∵弧AC所对的圆心角是∠AOC,圆周角是∠B
∴∠B= ∠AOC
推论:同弧或等弧所对的圆周角相等
D
A
B
C
E
·
O
图形语言:
几何语言:∵弧AC所对圆周角是∠D,∠B,∠E,∠C
∴∠D=∠B=∠E=∠C
1.如图,∠BAC=40°,则∠BOC= 。
A
B
C
O
当堂检测
2.如图,点B、C在⊙O上,且BO=BC,则圆周角 ∠BAC等于_____.
C
O
B
D
A
3.如图,A、B、C、D是⊙O上的四点,且∠BCD=100 °,则∠BOD=_____, ∠BAD____.
4.如图,在⊙O中,弦AB、CD相交于点E,∠ACD=40°,
∠CEB=75°,则∠CDB=______.
O
A
B
C
1
2
5.如图,OA、OB、OC都是⊙O的半径,∠AOB=2 ∠BOC.
∠1= ∠2有什么大小关系?请说明理由?
推论2:
半圆(或直径)所对的圆周角是直角;
90°的圆周角所对的弦是直径。
A
B
O
C1
C2
C3
推论
例 如图,AB为⊙O的直径,弦CD交AB于
点P, ∠ACD=60°,∠ADC=70°,
求∠APC的度数.
A
C
B
D
P
O
.
辅助线:构造直径所对圆周角
还有其他方法吗?
探索四:圆内接四边形与性质
四边形ABCD四个顶点都在⊙O上,
这样的四边形叫做圆内接四边形,
这个圆叫做四边形的外接圆.
圆内接四边形有什么性质?
如图A,B,C,D,是⊙O上的四点,AC为⊙O的直径,则∠BAD与∠BCD之间有什么关系?为什么?
解析:∵AC是⊙O的直径,
∴∠ADB = 90° ∠ABC = 90°
∴ ∠BAD + ∠BCD
=360°-90°-90°= 180°
如图A,B,C,D,是⊙O上的四点,点C的位置发生了变化,则∠BAD与∠BCD的关系还成立吗?为什么?
解析:成立
连结OB,OD
∵ 弧BAD与弧BCD所对的圆心角之和
为360°
∴ ∠BAD +∠BCD = 180°
圆内接四边形的性质:
圆内接四边形对角互补
如图∠DCE是圆内接四边形ABCD的一个外角,则∠A与∠DCE的大小有什么关系?
∴ ∠A = ∠DCE
例4、如图,四边形ABCD为⊙O圆的内接四边形∠BOD=100°
求∠BAD及∠BCD的度数.
解:∵圆心角∠BOD与圆周角∠BAD所对的弧为BD
∠BOD=100°
⌒
∴∠BAD= ∠BOD=50°
∵∠BCD+∠BAD=180°
∴∠BCD=180°-∠BAD= 130°
课堂小结:
1.圆周角定义: 顶点在圆上,并且两边都和圆相交的角叫圆周角.
2.圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半.
4.圆周角定理推论2:直径所对的圆周角为直角;90°的圆周角所对的弦是直径.
5.推论 圆内接四边形的对角互补
3.圆周角定理推论1:同弧(或等弧)所对的圆周角相等.
作业布置:
必做题:教材80页第1题,第2题.
选做题:教材80页第3题
第三章 圆
第4节 圆周角与圆心角之间的关系第一课时
O
1.圆心角的定义
.
B
C
答:在同圆或等圆中,相等的圆心角所对的弧也相等。
答:顶点在圆心的角叫圆心角.
2.圆心角和它所对的弧的关系
引入新课
2017年3月23日晚,国足在俄罗斯世预赛12强赛第六轮的比赛中以1-0打赢韩国,请大家观看视频
在射门游戏中,球员射中球门的难易与他所处的位置B对球门AC的张角(∠ABC)有关。
如图,当他站在B,D,E的位置射球时,对球门AC的张角的大小相等吗?
你能观察到这三个角有什么共同特征吗
你能仿照圆心角的定义给圆周角下定义吗
.
O
B
C
A
特征:
①角的顶点在圆上.
圆周角定义: 顶点在圆上,并且两边分别与圆
还有另一个交点的角叫圆周角.
②角的两边都与圆相交.
合作探究一:
讲授新课
判断下列各图形中的角是不是圆周角,并说明理由.
图1
图2
图3
图4
图5
追踪练习1
圆周角的性质
我们先研究一条弧所对的圆周角与它所对的圆心角之间的关系。
请同学们在圆上确定一条劣弧,画出它所对的圆心角与圆周角。
A
C
合作探究2
小组合作解决问题:
我们得到以下三种情况。
B
A
O
C
圆心O在∠B的一条边上
A
B
C
O
圆心O在∠B的内部。
B
A
C
O
圆心O在∠B的外部
问题2:这些圆周角的大小与圆心角∠AOC的大小有什么关系?
问题3:改变∠AOC的度数,你得到的结论还成立吗?
A
B
C
E
·
O
D
结论:(1)圆周角的度数等于它所对弧上圆心角度 数的一半.
(2)同弧或等弧所对的圆周角相等
圆周角和圆心角的关系
●O
A
B
C
结论:圆周角的度数等于它所对弧上圆心角度 数的一半.
1. 当圆心(O)在∠B的一边上时, ∠B与∠AOC的大小关系?
提示:能否转化为1的情况
结论:一条弧所对的圆周角等于它所对的圆心角的一半.
●O
A
B
C
2.当圆心O在圆周角∠B的内部时,∠B与∠AOC的大小关系
结论:圆周角的度数等于它所对弧上圆心角度数的一半.
D
●O
A
B
C
3.当圆心O在∠B的外部时,∠B与∠AOC的大小关系
圆周角定理:
圆周角的度数等于它所对弧上圆心角度数的一半.
B
A
O
C
圆心O在∠B的一条边上
A
B
C
O
圆心O在∠B的内部。
B
A
C
O
圆心O在∠B的外部
图形语言:
几何语言:∵弧AC所对的圆心角是∠AOC,圆周角是∠B
∴∠B= ∠AOC
推论:同弧或等弧所对的圆周角相等
D
A
B
C
E
·
O
图形语言:
几何语言:∵弧AC所对圆周角是∠D,∠B,∠E,∠C
∴∠D=∠B=∠E=∠C
1.如图,∠BAC=40°,则∠BOC= 。
A
B
C
O
当堂检测
2.如图,点B、C在⊙O上,且BO=BC,则圆周角 ∠BAC等于_____.
C
O
B
D
A
3.如图,A、B、C、D是⊙O上的四点,且∠BCD=100 °,则∠BOD=_____, ∠BAD____.
4.如图,在⊙O中,弦AB、CD相交于点E,∠ACD=40°,
∠CEB=75°,则∠CDB=______.
O
A
B
C
1
2
5.如图,OA、OB、OC都是⊙O的半径,∠AOB=2 ∠BOC.
∠1= ∠2有什么大小关系?请说明理由?
推论2:
半圆(或直径)所对的圆周角是直角;
90°的圆周角所对的弦是直径。
A
B
O
C1
C2
C3
推论
例 如图,AB为⊙O的直径,弦CD交AB于
点P, ∠ACD=60°,∠ADC=70°,
求∠APC的度数.
A
C
B
D
P
O
.
辅助线:构造直径所对圆周角
还有其他方法吗?
探索四:圆内接四边形与性质
四边形ABCD四个顶点都在⊙O上,
这样的四边形叫做圆内接四边形,
这个圆叫做四边形的外接圆.
圆内接四边形有什么性质?
如图A,B,C,D,是⊙O上的四点,AC为⊙O的直径,则∠BAD与∠BCD之间有什么关系?为什么?
解析:∵AC是⊙O的直径,
∴∠ADB = 90° ∠ABC = 90°
∴ ∠BAD + ∠BCD
=360°-90°-90°= 180°
如图A,B,C,D,是⊙O上的四点,点C的位置发生了变化,则∠BAD与∠BCD的关系还成立吗?为什么?
解析:成立
连结OB,OD
∵ 弧BAD与弧BCD所对的圆心角之和
为360°
∴ ∠BAD +∠BCD = 180°
圆内接四边形的性质:
圆内接四边形对角互补
如图∠DCE是圆内接四边形ABCD的一个外角,则∠A与∠DCE的大小有什么关系?
∴ ∠A = ∠DCE
例4、如图,四边形ABCD为⊙O圆的内接四边形∠BOD=100°
求∠BAD及∠BCD的度数.
解:∵圆心角∠BOD与圆周角∠BAD所对的弧为BD
∠BOD=100°
⌒
∴∠BAD= ∠BOD=50°
∵∠BCD+∠BAD=180°
∴∠BCD=180°-∠BAD= 130°
课堂小结:
1.圆周角定义: 顶点在圆上,并且两边都和圆相交的角叫圆周角.
2.圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半.
4.圆周角定理推论2:直径所对的圆周角为直角;90°的圆周角所对的弦是直径.
5.推论 圆内接四边形的对角互补
3.圆周角定理推论1:同弧(或等弧)所对的圆周角相等.
作业布置:
必做题:教材80页第1题,第2题.
选做题:教材80页第3题
