湘教版数学七年级下册 4.4平行线的判定教案(含2课时)
文档属性
| 名称 | 湘教版数学七年级下册 4.4平行线的判定教案(含2课时) |  | |
| 格式 | docx | ||
| 文件大小 | 110.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-17 13:35:23 | ||
图片预览

文档简介
4.4 平行线的判定
第1课时 平行线的判定方法1
【教学目标】
理解平行线的判定方法“同位角相等两直线平行”并学会运用这一判定方法进行简单的几何推理.
【教学重难点】
重点:同位角相等两直线平行.
难点:运用平行线的判定方法进行简单的推理.
【教学过程】
【情景导入,初步认识】
1.在同一平面内,两条直线的位置关系是________.
2.在同一平面内,________两条直线的是平行线.
3.如何判定两条直线是否平行呢?
教学说明
教师通过设置问题串,层层设疑,在引导学生思考、层层释疑的基础上,既复习旧知,做好新知学习的铺垫,同时也不断激活学生思维、生成新问题,引起认知冲突,从而自然引入新课.
【思考探究,获取新知】
1.动手操作移动活动木条,改变图中∠1的大小,使∠1=90°,那么∠2为多少度时,木条a与木条b平行?若∠1分别为60°、120°时,∠2为多少度,木条a与木条b平行?
按照上面的操作,∠1与∠2的大小满足什么关系时,木条a与木条b平行?小组内交流.
你能用几何推理的方法说明这个结论吗?
归纳结论
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.简称“同位角相等,两直线平行”.
2.想一想,观察教材第91页图428,
如何利用三角板画平行线?小明是这样做的,你认为他做得对不对?你能说明其中的原理吗?
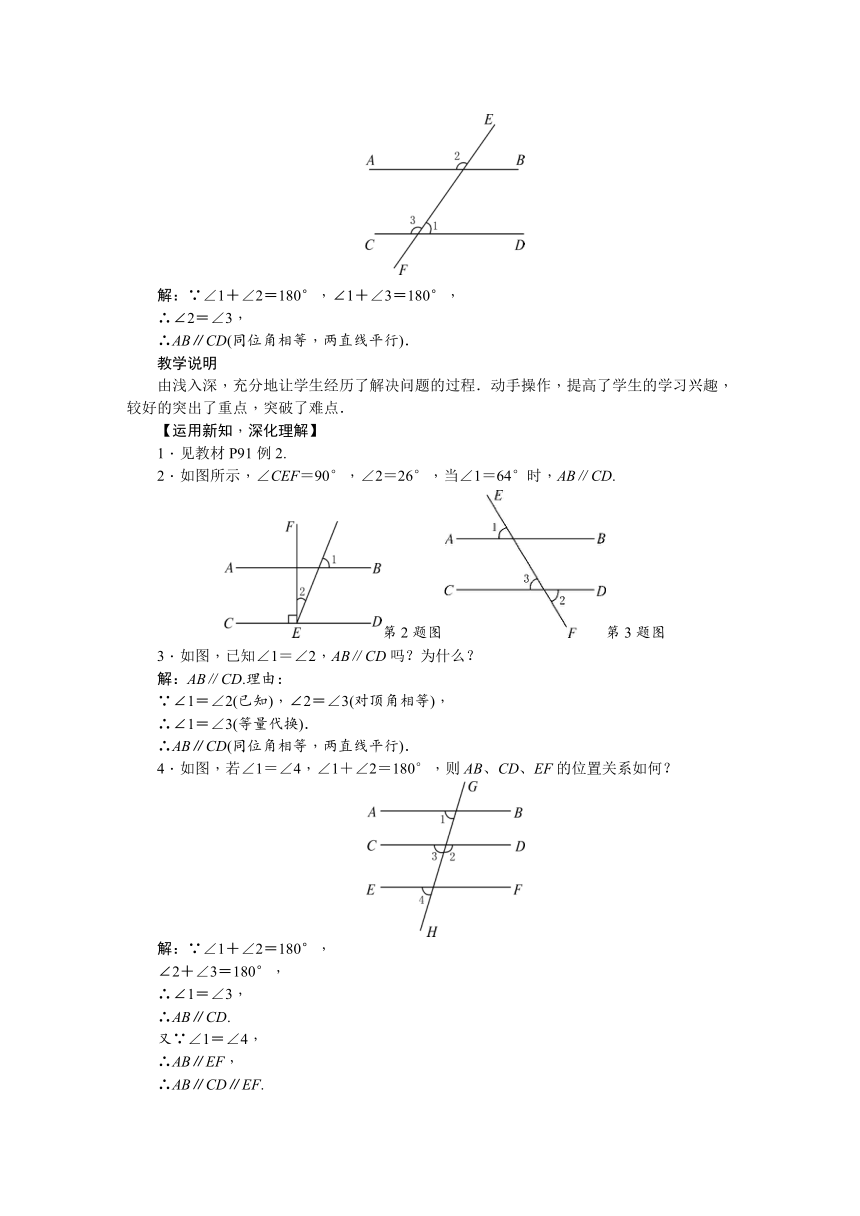
3.如图,直线AB、CD被直线EF所截,∠1+∠2=180°,AB与CD平行吗?为什么?
解:∵∠1+∠2=180°,∠1+∠3=180°,
∴∠2=∠3,
∴AB∥CD(同位角相等,两直线平行).
教学说明
由浅入深,充分地让学生经历了解决问题的过程.动手操作,提高了学生的学习兴趣,较好的突出了重点,突破了难点.
【运用新知,深化理解】
1.见教材P91例2.
2.如图所示,∠CEF=90°,∠2=26°,当∠1=64°时,AB∥CD.
第2题图第3题图
3.如图,已知∠1=∠2,AB∥CD吗?为什么?
解:AB∥CD.理由:
∵∠1=∠2(已知),∠2=∠3(对顶角相等),
∴∠1=∠3(等量代换).
∴AB∥CD(同位角相等,两直线平行).
4.如图,若∠1=∠4,∠1+∠2=180°,则AB、CD、EF的位置关系如何?
解:∵∠1+∠2=180°,
∠2+∠3=180°,
∴∠1=∠3,
∴AB∥CD.
又∵∠1=∠4,
∴AB∥EF,
∴AB∥CD∥EF.
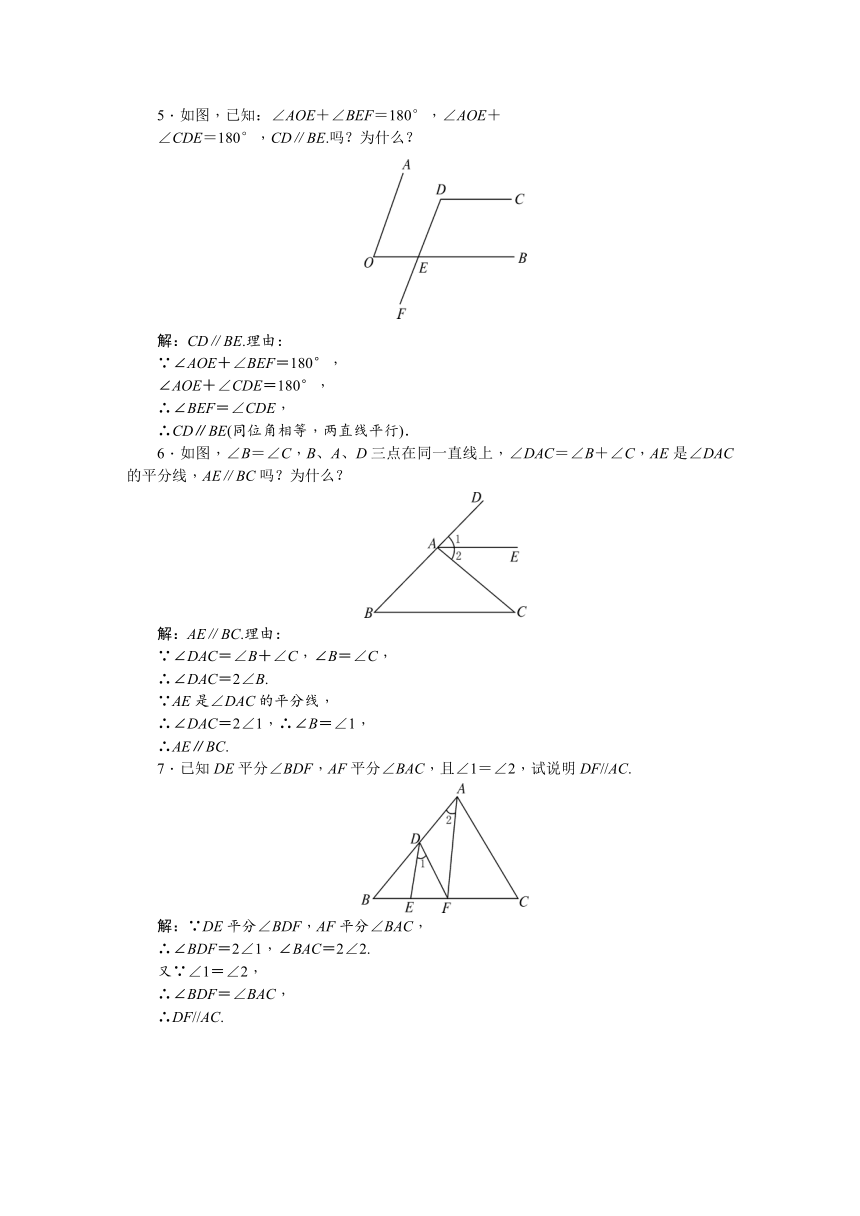
5.如图,已知:∠AOE+∠BEF=180°,∠AOE+
∠CDE=180°,CD∥BE.吗?为什么?
解:CD∥BE.理由:
∵∠AOE+∠BEF=180°,
∠AOE+∠CDE=180°,
∴∠BEF=∠CDE,
∴CD∥BE(同位角相等,两直线平行).
6.如图,∠B=∠C,B、A、D三点在同一直线上,∠DAC=∠B+∠C,AE是∠DAC的平分线,AE∥BC吗?为什么?
解:AE∥BC.理由:
∵∠DAC=∠B+∠C,∠B=∠C,
∴∠DAC=2∠B.
∵AE是∠DAC的平分线,
∴∠DAC=2∠1,∴∠B=∠1,
∴AE∥BC.
7.已知DE平分∠BDF,AF平分∠BAC,且∠1=∠2,试说明DF//AC.
解:∵DE平分∠BDF,AF平分∠BAC,
∴∠BDF=2∠1,∠BAC=2∠2.
又∵∠1=∠2,
∴∠BDF=∠BAC,
∴DF//AC.
教学说明
进一步激发学生的探究兴趣,学会用所学知识解释和解决实际生活中的问题,提高能力.
【师生互动,课堂小结】
先小组内交流收获和感想,而后以小组为单位派代表进行总结.教师作以补充.
【课后作业】
1.布置作业:教材P91“练习”.
2.完成同步练习册中本课时的练习.
第2课时 平行线的判定方法2、3
【教学目标】
1.使学生掌握利用内错角、同旁内角判定两直线平行的判定方法.
2.能运用所学过的平行线的判定方法,进行简单的推理和计算.
【教学重难点】
重点:会用“内错角相等,两直线平行”和“同旁内角互补,两直线平行”的判定方法.
难点:会用“内错角相等,两直线平行”和“同旁内角互补,两直线平行”的判定方法.
【教学过程】
【情景导入,初步认识】
小明有一块小画板,他想知道它的上下边缘是否平行,于是他在两个边缘之间画了一条线段AB(如图所示).他只有一个量角器,他通过测量某些角的大小就能知道这个画板的上下边缘是否平行,你知道他是怎样做的吗?
教学说明
通过实际问题的引入,提高学生学习的兴趣.
【思考探究,获取新知】
1.通过合作学习,提出猜想.
如图中,直线AB与CD被直线EF所截,若∠2=∠3,则AB与CD平行吗?
你可以从以下几个方面考虑:
(1)我们已经有怎样的判定两直线平行的方法?
(2)有∠2=∠3,能得出有一对同位角相等吗?
(3)你能证明吗?
因为∠1与∠3是对顶角,
所以∠1=∠3,
因为∠2=∠3,所以∠1=∠2.
所以AB∥CD(同位角相等,两直线平行).
由此你又获得怎样的判定平行线的方法?
归纳结论
两条直线被第三条直线所截,如果内错角相等,则两条直线平行.简单的说,内错角相等,两条直线平行.
教师强调几何语言的表述方法:
∵∠2=∠3,
∴AB∥CD(内错角相等,两条直线平行).
2.如图中,直线AB与CD被直线EF所截,若∠1+∠2=180°,则AB与CD平行吗?
你可以从以下几个方面考虑:
(1)我们已经有怎样的判定两直线平行的方法?
(2)有∠1+∠2=180°,能得出有一对同位角相等吗?
(4)你能说明理由吗?
因为∠1+∠2=180°,且∠3+∠2=180°,
所以∠1=∠3.
所以AB∥CD(同位角相等,两直线平行).
由此你又获得怎样的判定平行线的方法?
归纳结论
两条直线被第三条直线所截,如果同旁内角互补,则两条直线平行.简单的说,同旁内角互补,两条直线平行.
教师强调几何语言的表述方法:
∵∠1+∠2=180°,
∴AB∥CD(同旁内角互补,两条直线平行).
教学说明
在学生交流的基础上,教师再利用课件展示,进一步验证结论,从而引导学生得出结论.
【运用新知,深化理解】
1.见教材P93例3、例4.
2.如图所示,下列条件中不能判定DE∥BC的是( C )
A.∠1=∠C B.∠2=∠3
C.∠1=∠2 D.∠2+∠4=180°
第2题图第3题图
3.如图,一个弯形管道ABCD的拐角∠ABC=120°,∠BCD=60°,这时说管道AB∥CD对吗?为什么?
解:说管道AB∥CD是对的.
理由:∵∠ABC=120°,∠BCD=60°,
∴∠ABC+∠BCD=180°,
∴AB∥CD(同旁内角互补,两直线平行).
4.如图所示,∠ABC=90°,∠BCD=90°,∠1=∠2,那么EB∥CF吗?为什么?
解:EB∥CF,理由如下:
∵∠ABC=∠BCD=90°,
∴∠1+∠3=∠2+∠4=90°,
∵∠1=∠2,∴∠3=∠4,
∴EB∥CF(内错角相等,两直线平行).
5.已知:如图,∠ABC=90°,∠1+∠2=90°,∠2=∠3.BE∥DF吗?为什么?
解:BE∥DF.理由:
∵∠1+∠2=90°,∠2=∠3,
∴∠1+∠3=90°,
又∵∠ABC=90°,
∴∠3+∠4=90°,
∴∠1=∠4,∴BE∥DF(同位角相等,两直线平行).
6.如图所示,BE是∠ABD的平分线,DE是∠BDC的平分线,且∠1+∠2=90°,那么直线AB,CD的位置关系如何?并说明理由.
解:AB∥CD.理由如下:
∵BE是∠ABD的平分线,DE是∠BDC的平分线,
∴∠ABD=2∠1,∠BDC=2∠2.
又∵∠1+∠2=90°,
∴∠ABD+∠BDC=180°,
∴AB∥CD(同旁内角互补,两直线平行).
教学说明
通过练习及时巩固所学知识,并学会灵活应用.
【师生互动,课堂小结】
先小组内交流收获和感想,而后以小组为单位派代表进行总结.教师作以补充.
【课后作业】
1.布置作业:教材“习题4.4”中第5、7、8题.
2.完成同步练习册中本课时的练习.
第1课时 平行线的判定方法1
【教学目标】
理解平行线的判定方法“同位角相等两直线平行”并学会运用这一判定方法进行简单的几何推理.
【教学重难点】
重点:同位角相等两直线平行.
难点:运用平行线的判定方法进行简单的推理.
【教学过程】
【情景导入,初步认识】
1.在同一平面内,两条直线的位置关系是________.
2.在同一平面内,________两条直线的是平行线.
3.如何判定两条直线是否平行呢?
教学说明
教师通过设置问题串,层层设疑,在引导学生思考、层层释疑的基础上,既复习旧知,做好新知学习的铺垫,同时也不断激活学生思维、生成新问题,引起认知冲突,从而自然引入新课.
【思考探究,获取新知】
1.动手操作移动活动木条,改变图中∠1的大小,使∠1=90°,那么∠2为多少度时,木条a与木条b平行?若∠1分别为60°、120°时,∠2为多少度,木条a与木条b平行?
按照上面的操作,∠1与∠2的大小满足什么关系时,木条a与木条b平行?小组内交流.
你能用几何推理的方法说明这个结论吗?
归纳结论
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.简称“同位角相等,两直线平行”.
2.想一想,观察教材第91页图428,
如何利用三角板画平行线?小明是这样做的,你认为他做得对不对?你能说明其中的原理吗?
3.如图,直线AB、CD被直线EF所截,∠1+∠2=180°,AB与CD平行吗?为什么?
解:∵∠1+∠2=180°,∠1+∠3=180°,
∴∠2=∠3,
∴AB∥CD(同位角相等,两直线平行).
教学说明
由浅入深,充分地让学生经历了解决问题的过程.动手操作,提高了学生的学习兴趣,较好的突出了重点,突破了难点.
【运用新知,深化理解】
1.见教材P91例2.
2.如图所示,∠CEF=90°,∠2=26°,当∠1=64°时,AB∥CD.
第2题图第3题图
3.如图,已知∠1=∠2,AB∥CD吗?为什么?
解:AB∥CD.理由:
∵∠1=∠2(已知),∠2=∠3(对顶角相等),
∴∠1=∠3(等量代换).
∴AB∥CD(同位角相等,两直线平行).
4.如图,若∠1=∠4,∠1+∠2=180°,则AB、CD、EF的位置关系如何?
解:∵∠1+∠2=180°,
∠2+∠3=180°,
∴∠1=∠3,
∴AB∥CD.
又∵∠1=∠4,
∴AB∥EF,
∴AB∥CD∥EF.
5.如图,已知:∠AOE+∠BEF=180°,∠AOE+
∠CDE=180°,CD∥BE.吗?为什么?
解:CD∥BE.理由:
∵∠AOE+∠BEF=180°,
∠AOE+∠CDE=180°,
∴∠BEF=∠CDE,
∴CD∥BE(同位角相等,两直线平行).
6.如图,∠B=∠C,B、A、D三点在同一直线上,∠DAC=∠B+∠C,AE是∠DAC的平分线,AE∥BC吗?为什么?
解:AE∥BC.理由:
∵∠DAC=∠B+∠C,∠B=∠C,
∴∠DAC=2∠B.
∵AE是∠DAC的平分线,
∴∠DAC=2∠1,∴∠B=∠1,
∴AE∥BC.
7.已知DE平分∠BDF,AF平分∠BAC,且∠1=∠2,试说明DF//AC.
解:∵DE平分∠BDF,AF平分∠BAC,
∴∠BDF=2∠1,∠BAC=2∠2.
又∵∠1=∠2,
∴∠BDF=∠BAC,
∴DF//AC.
教学说明
进一步激发学生的探究兴趣,学会用所学知识解释和解决实际生活中的问题,提高能力.
【师生互动,课堂小结】
先小组内交流收获和感想,而后以小组为单位派代表进行总结.教师作以补充.
【课后作业】
1.布置作业:教材P91“练习”.
2.完成同步练习册中本课时的练习.
第2课时 平行线的判定方法2、3
【教学目标】
1.使学生掌握利用内错角、同旁内角判定两直线平行的判定方法.
2.能运用所学过的平行线的判定方法,进行简单的推理和计算.
【教学重难点】
重点:会用“内错角相等,两直线平行”和“同旁内角互补,两直线平行”的判定方法.
难点:会用“内错角相等,两直线平行”和“同旁内角互补,两直线平行”的判定方法.
【教学过程】
【情景导入,初步认识】
小明有一块小画板,他想知道它的上下边缘是否平行,于是他在两个边缘之间画了一条线段AB(如图所示).他只有一个量角器,他通过测量某些角的大小就能知道这个画板的上下边缘是否平行,你知道他是怎样做的吗?
教学说明
通过实际问题的引入,提高学生学习的兴趣.
【思考探究,获取新知】
1.通过合作学习,提出猜想.
如图中,直线AB与CD被直线EF所截,若∠2=∠3,则AB与CD平行吗?
你可以从以下几个方面考虑:
(1)我们已经有怎样的判定两直线平行的方法?
(2)有∠2=∠3,能得出有一对同位角相等吗?
(3)你能证明吗?
因为∠1与∠3是对顶角,
所以∠1=∠3,
因为∠2=∠3,所以∠1=∠2.
所以AB∥CD(同位角相等,两直线平行).
由此你又获得怎样的判定平行线的方法?
归纳结论
两条直线被第三条直线所截,如果内错角相等,则两条直线平行.简单的说,内错角相等,两条直线平行.
教师强调几何语言的表述方法:
∵∠2=∠3,
∴AB∥CD(内错角相等,两条直线平行).
2.如图中,直线AB与CD被直线EF所截,若∠1+∠2=180°,则AB与CD平行吗?
你可以从以下几个方面考虑:
(1)我们已经有怎样的判定两直线平行的方法?
(2)有∠1+∠2=180°,能得出有一对同位角相等吗?
(4)你能说明理由吗?
因为∠1+∠2=180°,且∠3+∠2=180°,
所以∠1=∠3.
所以AB∥CD(同位角相等,两直线平行).
由此你又获得怎样的判定平行线的方法?
归纳结论
两条直线被第三条直线所截,如果同旁内角互补,则两条直线平行.简单的说,同旁内角互补,两条直线平行.
教师强调几何语言的表述方法:
∵∠1+∠2=180°,
∴AB∥CD(同旁内角互补,两条直线平行).
教学说明
在学生交流的基础上,教师再利用课件展示,进一步验证结论,从而引导学生得出结论.
【运用新知,深化理解】
1.见教材P93例3、例4.
2.如图所示,下列条件中不能判定DE∥BC的是( C )
A.∠1=∠C B.∠2=∠3
C.∠1=∠2 D.∠2+∠4=180°
第2题图第3题图
3.如图,一个弯形管道ABCD的拐角∠ABC=120°,∠BCD=60°,这时说管道AB∥CD对吗?为什么?
解:说管道AB∥CD是对的.
理由:∵∠ABC=120°,∠BCD=60°,
∴∠ABC+∠BCD=180°,
∴AB∥CD(同旁内角互补,两直线平行).
4.如图所示,∠ABC=90°,∠BCD=90°,∠1=∠2,那么EB∥CF吗?为什么?
解:EB∥CF,理由如下:
∵∠ABC=∠BCD=90°,
∴∠1+∠3=∠2+∠4=90°,
∵∠1=∠2,∴∠3=∠4,
∴EB∥CF(内错角相等,两直线平行).
5.已知:如图,∠ABC=90°,∠1+∠2=90°,∠2=∠3.BE∥DF吗?为什么?
解:BE∥DF.理由:
∵∠1+∠2=90°,∠2=∠3,
∴∠1+∠3=90°,
又∵∠ABC=90°,
∴∠3+∠4=90°,
∴∠1=∠4,∴BE∥DF(同位角相等,两直线平行).
6.如图所示,BE是∠ABD的平分线,DE是∠BDC的平分线,且∠1+∠2=90°,那么直线AB,CD的位置关系如何?并说明理由.
解:AB∥CD.理由如下:
∵BE是∠ABD的平分线,DE是∠BDC的平分线,
∴∠ABD=2∠1,∠BDC=2∠2.
又∵∠1+∠2=90°,
∴∠ABD+∠BDC=180°,
∴AB∥CD(同旁内角互补,两直线平行).
教学说明
通过练习及时巩固所学知识,并学会灵活应用.
【师生互动,课堂小结】
先小组内交流收获和感想,而后以小组为单位派代表进行总结.教师作以补充.
【课后作业】
1.布置作业:教材“习题4.4”中第5、7、8题.
2.完成同步练习册中本课时的练习.
