苏教版五年级下学期数学7解决问题的策略课件(共21张PPT)
文档属性
| 名称 | 苏教版五年级下学期数学7解决问题的策略课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 33.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-16 11:27:17 | ||
图片预览




文档简介
(共21张PPT)
7 解决问题的策略
讲授新课
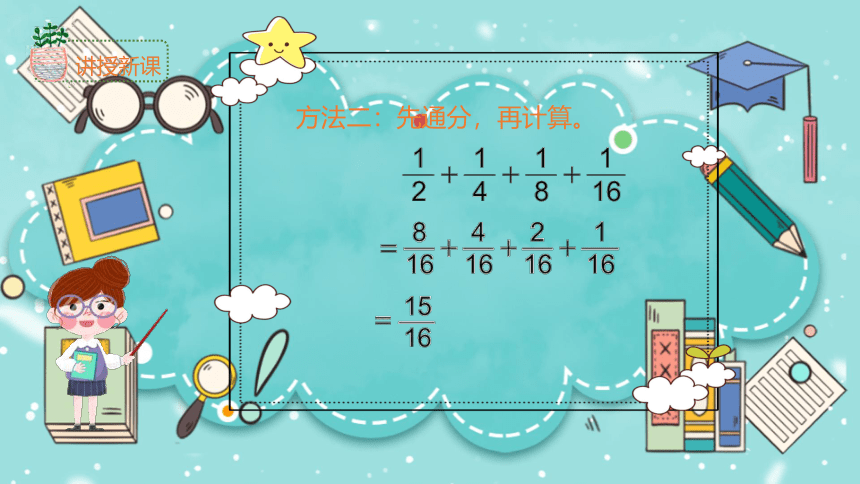
方法二:先通分,再计算。
情境导入
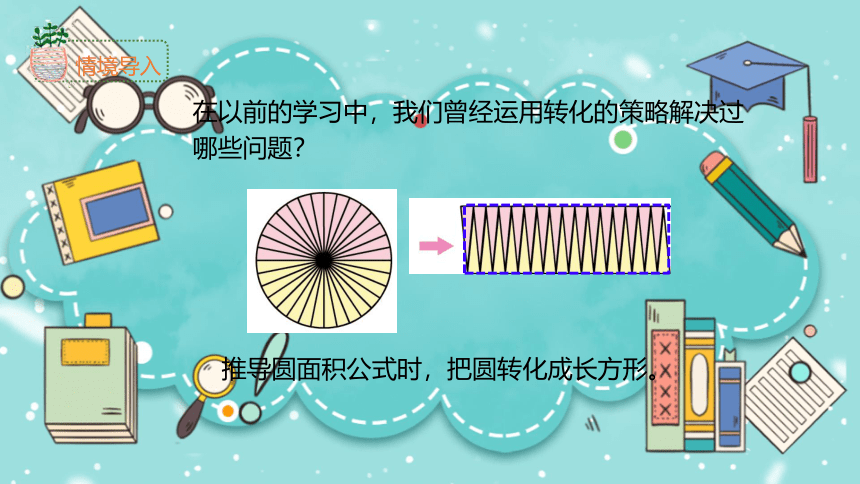
在以前的学习中,我们曾经运用转化的策略解决过哪些问题?
推导圆面积公式时,把圆转化成长方形。
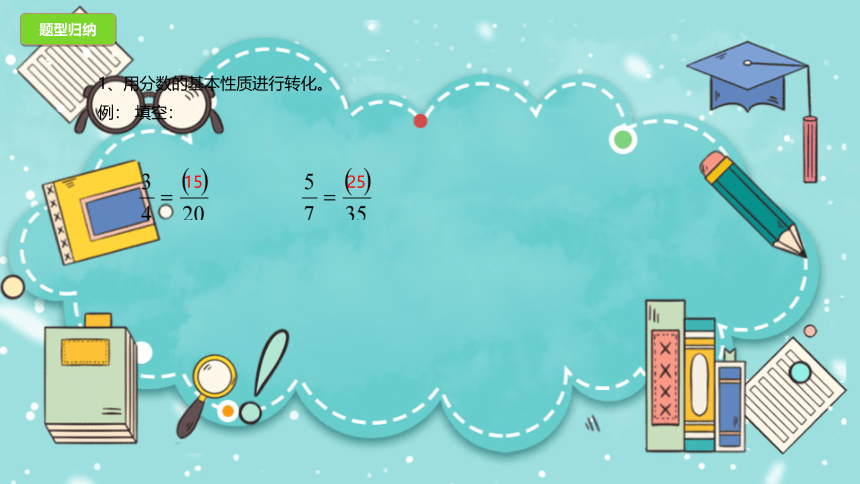
1、用分数的基本性质进行转化。
例: 填空:
题型归纳
15
25
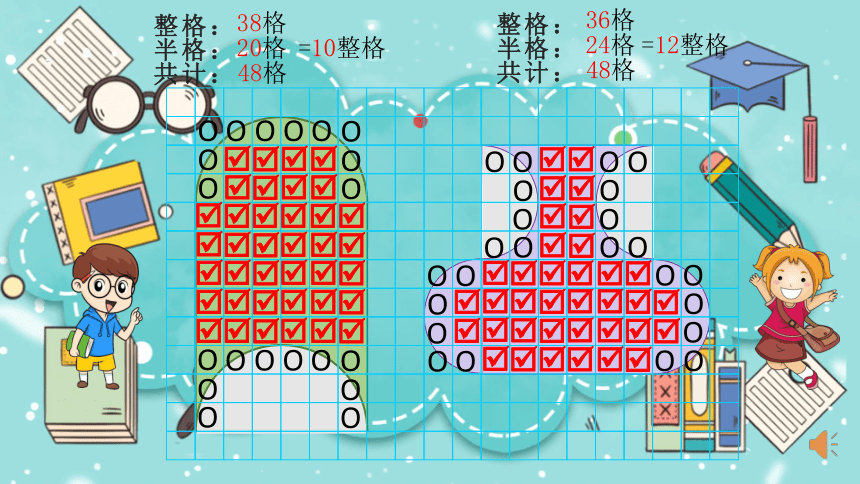
整格:
半格:
共计:
38格
20格
48格
36格
24格
48格
整格:
半格:
共计:
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
=10整格
=12整格
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
下面两个图形,哪个面积大一些
1.解决例1提出的问题,我们应用了什么策略?
平移,旋转
2.用什么方法把不规则图形转化成规则图形?
转化
3.转化后的图形和转化前比,什么变了?
什么没变?
形状变了,大小没变
讲授新课
随堂检测
2、计算下面图形的周长。
1×4=4(米)
答:这个图形的周长是4米。
操作回顾
回顾解决问题的过程,我们运用了什么策略?你有什么体会
当堂练习
2.下图是一个装满了铅笔的铅笔架。你能联系梯形面积公式,计算出铅笔的支数吗?
(15+6)×10÷2
=210÷2
=105(支)
答:总共有105支铅笔。
当堂练习
图中,4个扇形的半径相等,均为3厘米,求涂色部分的面积。
3.14×3 =28.26(平方厘米)
请同学们回顾一下,我们曾经运用转化的策略解决过哪些问题?
温故知新
当堂小结
运用转化的策略,借助数形结合从不同的角度灵活地分析问题,可以使复杂的计算简单化。。
3.84
÷
1.6
=2.4
)
3.8.4
1.6
2.4
6 4
3 2
6 4
0
除数是小数的除法转化成除数是整数的除法
38.4
÷
16
=2.4
)
38.4
16
2.4
6 4
32
6 4
0
温故知新
异分母分数加减法可以转化成什么?
2
1
+
3
1
=
6
3
6
2
+
=
6
5
2
1
4
1
=
4
2
4
1
=
4
1
转化转化
推导梯形的面积公式时,把梯形转化成平行四边形。
转化转化
2.用分数表示图中的涂色部分。
学以致用
( )
( )
1
2
课后作业
教材109页。
Goodbye~
感谢聆听,下期再会
7 解决问题的策略
讲授新课
方法二:先通分,再计算。
情境导入
在以前的学习中,我们曾经运用转化的策略解决过哪些问题?
推导圆面积公式时,把圆转化成长方形。
1、用分数的基本性质进行转化。
例: 填空:
题型归纳
15
25
整格:
半格:
共计:
38格
20格
48格
36格
24格
48格
整格:
半格:
共计:
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
=10整格
=12整格
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
下面两个图形,哪个面积大一些
1.解决例1提出的问题,我们应用了什么策略?
平移,旋转
2.用什么方法把不规则图形转化成规则图形?
转化
3.转化后的图形和转化前比,什么变了?
什么没变?
形状变了,大小没变
讲授新课
随堂检测
2、计算下面图形的周长。
1×4=4(米)
答:这个图形的周长是4米。
操作回顾
回顾解决问题的过程,我们运用了什么策略?你有什么体会
当堂练习
2.下图是一个装满了铅笔的铅笔架。你能联系梯形面积公式,计算出铅笔的支数吗?
(15+6)×10÷2
=210÷2
=105(支)
答:总共有105支铅笔。
当堂练习
图中,4个扇形的半径相等,均为3厘米,求涂色部分的面积。
3.14×3 =28.26(平方厘米)
请同学们回顾一下,我们曾经运用转化的策略解决过哪些问题?
温故知新
当堂小结
运用转化的策略,借助数形结合从不同的角度灵活地分析问题,可以使复杂的计算简单化。。
3.84
÷
1.6
=2.4
)
3.8.4
1.6
2.4
6 4
3 2
6 4
0
除数是小数的除法转化成除数是整数的除法
38.4
÷
16
=2.4
)
38.4
16
2.4
6 4
32
6 4
0
温故知新
异分母分数加减法可以转化成什么?
2
1
+
3
1
=
6
3
6
2
+
=
6
5
2
1
4
1
=
4
2
4
1
=
4
1
转化转化
推导梯形的面积公式时,把梯形转化成平行四边形。
转化转化
2.用分数表示图中的涂色部分。
学以致用
( )
( )
1
2
课后作业
教材109页。
Goodbye~
感谢聆听,下期再会
