2021-2022学年高二上学期物理人教版(2019)选择性必修第一册2.3简谐运动的回复力和能量同步练习(word版含答案)
文档属性
| 名称 | 2021-2022学年高二上学期物理人教版(2019)选择性必修第一册2.3简谐运动的回复力和能量同步练习(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 169.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-05-16 14:55:33 | ||
图片预览

文档简介
回复力与能量
一、多选题
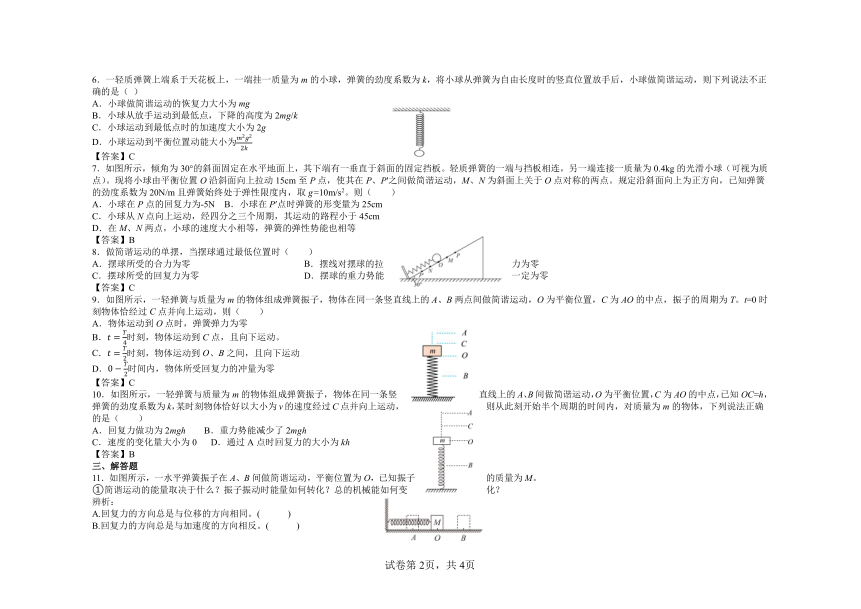
1.如图所示,物体A与滑块B一起在光滑水平面上做简谐运动,振动周期为T,A、B之间的的动摩擦因数为(己知最大静摩擦力等于滑动摩擦力),已知轻质弹簧的劲度系数为k,A、B的质量分别为m和M,下列说法正确的是( )
A.物体A受到重力、摩擦力、回复力作用
B.A、B间无相对滑动的最大振幅为
C.某时刻,B的速度为v,经过后,B的速度再次为v,则可能小于
D.当物体B相对平衡位置的位移为x时,A、B间摩擦力的大小等于
【答案】BC
2.如图所示,倾角为θ的光滑绝缘斜面顶端固定一劲度系数为k1的绝缘轻质弹簧,弹簧另外一端连接一质量为m、带电荷量为+Q的小球P,斜面底端固定一带电小球S,带电荷量为-q,当小球P静止时,两者相距r。现突然将小球S移走,小球P做简谐运动,已知静电力常量为k,弹簧的原长为x0,小球可视为质点,重力加速度为g,则( )
A.小球P受到的回复力满足F回=-kx,式中k为弹簧的劲度系数
B.小球P做简谐运动的振幅为
C.小球P做简谐运动的平衡位置距离斜面顶端+x0
D.若不撤去小球S,给小球P沿斜面向下的初速度,小球P仍做简谐运动
【答案】AB
二、单选题
3.把一个小球套在光滑细杆上,球与轻弹簧相连组成弹簧振子,小球沿杆在水平方向做简谐运动,它围绕平衡位置O在A、B间振动,如图所示,下列结论正确的是( )
A.小球在O位置时,动能最大,加速度最大
B.小球在A、B位置时,势能最大,加速度最小
C.小球从A经O到B的过程中,回复力先做正功后做负功
D.小球从B到O的过程中,振动的能量不断减小
【答案】C
4.如图所示,在粗细均匀的一根木筷下端绕几圈铁丝,竖直浮在较大的装有水的杯中。把木筷往上提起一段距离(木筷下端未离开水面)后放手,木筷就在水中上下振动。不考虑在振动过程中的能量损失,则( )
A.木筷的振动不是简谐运动
B.木筷振动的回复力为水对木筷的浮力
C.木筷在振动过程中所受的合力与振动位移成正比
D.木筷振动到最低点时底端距水面的距离为振幅
【答案】C
5.下列关于简谐运动所受回复力的说法中正确的是( )
A.回复力是由物体的弹性形变产生的 B.回复力的方向总是和速度的方向相反
C.回复力由物体受到的合外力提供 D.回复力的方向总是指向平衡位置
【答案】D
6.一轻质弹簧上端系于天花板上,一端挂一质量为m的小球,弹簧的劲度系数为k,将小球从弹簧为自由长度时的竖直位置放手后,小球做简谐运动,则下列说法不正确的是( )
A.小球做简谐运动的恢复力大小为mg
B.小球从放手运动到最低点,下降的高度为2mg/k
C.小球运动到最低点时的加速度大小为2g
D.小球运动到平衡位置动能大小为
【答案】C
7.如图所示,倾角为30°的斜面固定在水平地面上,其下端有一垂直于斜面的固定挡板。轻质弹簧的一端与挡板相连,另一端连接一质量为0.4kg的光滑小球(可视为质点)。现将小球由平衡位置O沿斜面向上拉动15cm至P点,使其在P、P′之间做简谐运动,M、N为斜面上关于O点对称的两点。规定沿斜面向上为正方向,已知弹簧的劲度系数为20N/m且弹簧始终处于弹性限度内,取g=10m/s2。则( )
A.小球在P点的回复力为-5N B.小球在P′点时弹簧的形变量为25cm
C.小球从N点向上运动,经四分之三个周期,其运动的路程小于45cm
D.在M、N两点,小球的速度大小相等,弹簧的弹性势能也相等
【答案】B
8.做简谐运动的单摆,当摆球通过最低位置时( )
A.摆球所受的合力为零 B.摆线对摆球的拉力为零
C.摆球所受的回复力为零 D.摆球的重力势能一定为零
【答案】C
9.如图所示,一轻弹簧与质量为m的物体组成弹簧振子,物体在同一条竖直线上的A、B两点间做简谐运动,O为平衡位置,C为AO的中点,振子的周期为T。t=0时刻物体恰经过C点并向上运动,则( )
A.物体运动到O点时,弹簧弹力为零
B.时刻,物体运动到C点,且向下运动。
C.时刻,物体运动到O、B之间,且向下运动
D.时间内,物体所受回复力的冲量为零
【答案】C
10.如图所示,一轻弹簧与质量为m的物体组成弹簧振子,物体在同一条竖直线上的A、B间做简谐运动,O为平衡位置,C为AO的中点,已知OC=h,弹簧的劲度系数为k,某时刻物体恰好以大小为v的速度经过C点并向上运动,则从此刻开始半个周期的时间内,对质量为m的物体,下列说法正确的是( )
A.回复力做功为2mgh B.重力势能减少了2mgh
C.速度的变化量大小为0 D.通过A点时回复力的大小为kh
【答案】B
解答题
11.如图所示,一水平弹簧振子在A、B间做简谐运动,平衡位置为O,已知振子的质量为M。
①简谐运动的能量取决于什么?振子振动时能量如何转化?总的机械能如何变化?
辨析:
A.回复力的方向总是与位移的方向相同。( )
B.回复力的方向总是与加速度的方向相反。( )
C.水平弹簧振子运动到平衡位置时,回复力不为零,能量为零。( )
D.回复力的大小与速度大小无关,速度增大时,回复力可能增大,也可能减小。( )
E.振子在平衡位置,动能最大,弹性势能最小
F.振子在最大位移处,弹性势能最大,动能最小
G.振子在向平衡位置运动时,由于振子振幅减小,故总机械能减小
H.在任意时刻,动能与弹性势能之和保持不变
(2)若振子运动到B处时将一质量为m的物体放到M的上面,且m和M无相对滑动而一起运动,振幅和最大动能如何变化?
12.物理学中,力与运动关系密切,而力的空间积累效果——做功,又是能量转化的量度。因此我们研究某些运动时,可以先分析研究对象的受力特点,进而分析其能量问题。已知重力加速度为,且在下列情境中,均不计空气阻力。
(1)劲度系数为的轻质弹簧上端固定,下端连一可视为质点的小物块,若以小物块的平衡位置为坐标原点,以竖直向下为正方向建立坐标轴,如图所示,用表示小物块由平衡位置向下发生的位移。求小物块的合力与的关系式,并据此说明小物块的运动是否为简谐运动;
(2)系统的总势能为重力势能与弹性势能之和。请你结合小物块的受力特点和求解变力功的基本方法,以平衡位置为系统总势能的零势能参考点,推到小物块振动位移为时系统总势能的表达式。
13.简谐运动是我们研究过的一种典型运动方式。一个质点做机械振动,如果它的回复力与偏离平衡位置的位移大小成正比,而且方向与位移方向相反,就能判定它是简谐运动。如图所示,将两个劲度系数分别为k1和k2的轻质弹簧套在光滑的水平杆上,弹簧的两端固定,中间接一质量为m的小球,此时两弹簧均处于原长。现将小球沿杆拉开一段距离后松开,小球以O为平衡位置往复运动。请你据此证明,小球所做的运动是简谐运动。
14.如图所示,轻弹簧上面固定一质量为m的小球,小球在竖直方向上做简谐运动,振幅为A,运动过程的最高点弹簧正好为原长,则小球在振动过程中,由哪些力提供回复力?平衡位置在哪里?
15.一根弹簧的上端固定,下端系一小球,将小球向下拉一点距离后放手,小球便上下振动起来。试证明这个小球在做简谐运动。(提示:使小球振动的回复力是小球所受到的重力和弹簧弹力的合力)
16.质量为m的小球被劲度系数分别是k1和k2的轻弹簧拴住,置于光滑水平面上,如图所示,此时两个弹簧均处于原长状态,记为位置O。
(1)证明:若将小球在水平方向上拉离位置O再释放,小球将做简谐运动。
(2)已知简谐运动的周期是:,其中k是回复力与位移的比例系数。求出此弹簧振子的周期。
(3)定义:振动物体出现在某区域的时间△t与观察时间t的比值,为振动物体在该区域出现的概率。那么在小球的振动过程中,当观察时间为振动周期的整数倍时,求:小球出现在位置O与右侧0.5A(A为振幅)的区域内的概率P。
试卷第1页,共3页
试卷第1页,共3页
一、多选题
1.如图所示,物体A与滑块B一起在光滑水平面上做简谐运动,振动周期为T,A、B之间的的动摩擦因数为(己知最大静摩擦力等于滑动摩擦力),已知轻质弹簧的劲度系数为k,A、B的质量分别为m和M,下列说法正确的是( )
A.物体A受到重力、摩擦力、回复力作用
B.A、B间无相对滑动的最大振幅为
C.某时刻,B的速度为v,经过后,B的速度再次为v,则可能小于
D.当物体B相对平衡位置的位移为x时,A、B间摩擦力的大小等于
【答案】BC
2.如图所示,倾角为θ的光滑绝缘斜面顶端固定一劲度系数为k1的绝缘轻质弹簧,弹簧另外一端连接一质量为m、带电荷量为+Q的小球P,斜面底端固定一带电小球S,带电荷量为-q,当小球P静止时,两者相距r。现突然将小球S移走,小球P做简谐运动,已知静电力常量为k,弹簧的原长为x0,小球可视为质点,重力加速度为g,则( )
A.小球P受到的回复力满足F回=-kx,式中k为弹簧的劲度系数
B.小球P做简谐运动的振幅为
C.小球P做简谐运动的平衡位置距离斜面顶端+x0
D.若不撤去小球S,给小球P沿斜面向下的初速度,小球P仍做简谐运动
【答案】AB
二、单选题
3.把一个小球套在光滑细杆上,球与轻弹簧相连组成弹簧振子,小球沿杆在水平方向做简谐运动,它围绕平衡位置O在A、B间振动,如图所示,下列结论正确的是( )
A.小球在O位置时,动能最大,加速度最大
B.小球在A、B位置时,势能最大,加速度最小
C.小球从A经O到B的过程中,回复力先做正功后做负功
D.小球从B到O的过程中,振动的能量不断减小
【答案】C
4.如图所示,在粗细均匀的一根木筷下端绕几圈铁丝,竖直浮在较大的装有水的杯中。把木筷往上提起一段距离(木筷下端未离开水面)后放手,木筷就在水中上下振动。不考虑在振动过程中的能量损失,则( )
A.木筷的振动不是简谐运动
B.木筷振动的回复力为水对木筷的浮力
C.木筷在振动过程中所受的合力与振动位移成正比
D.木筷振动到最低点时底端距水面的距离为振幅
【答案】C
5.下列关于简谐运动所受回复力的说法中正确的是( )
A.回复力是由物体的弹性形变产生的 B.回复力的方向总是和速度的方向相反
C.回复力由物体受到的合外力提供 D.回复力的方向总是指向平衡位置
【答案】D
6.一轻质弹簧上端系于天花板上,一端挂一质量为m的小球,弹簧的劲度系数为k,将小球从弹簧为自由长度时的竖直位置放手后,小球做简谐运动,则下列说法不正确的是( )
A.小球做简谐运动的恢复力大小为mg
B.小球从放手运动到最低点,下降的高度为2mg/k
C.小球运动到最低点时的加速度大小为2g
D.小球运动到平衡位置动能大小为
【答案】C
7.如图所示,倾角为30°的斜面固定在水平地面上,其下端有一垂直于斜面的固定挡板。轻质弹簧的一端与挡板相连,另一端连接一质量为0.4kg的光滑小球(可视为质点)。现将小球由平衡位置O沿斜面向上拉动15cm至P点,使其在P、P′之间做简谐运动,M、N为斜面上关于O点对称的两点。规定沿斜面向上为正方向,已知弹簧的劲度系数为20N/m且弹簧始终处于弹性限度内,取g=10m/s2。则( )
A.小球在P点的回复力为-5N B.小球在P′点时弹簧的形变量为25cm
C.小球从N点向上运动,经四分之三个周期,其运动的路程小于45cm
D.在M、N两点,小球的速度大小相等,弹簧的弹性势能也相等
【答案】B
8.做简谐运动的单摆,当摆球通过最低位置时( )
A.摆球所受的合力为零 B.摆线对摆球的拉力为零
C.摆球所受的回复力为零 D.摆球的重力势能一定为零
【答案】C
9.如图所示,一轻弹簧与质量为m的物体组成弹簧振子,物体在同一条竖直线上的A、B两点间做简谐运动,O为平衡位置,C为AO的中点,振子的周期为T。t=0时刻物体恰经过C点并向上运动,则( )
A.物体运动到O点时,弹簧弹力为零
B.时刻,物体运动到C点,且向下运动。
C.时刻,物体运动到O、B之间,且向下运动
D.时间内,物体所受回复力的冲量为零
【答案】C
10.如图所示,一轻弹簧与质量为m的物体组成弹簧振子,物体在同一条竖直线上的A、B间做简谐运动,O为平衡位置,C为AO的中点,已知OC=h,弹簧的劲度系数为k,某时刻物体恰好以大小为v的速度经过C点并向上运动,则从此刻开始半个周期的时间内,对质量为m的物体,下列说法正确的是( )
A.回复力做功为2mgh B.重力势能减少了2mgh
C.速度的变化量大小为0 D.通过A点时回复力的大小为kh
【答案】B
解答题
11.如图所示,一水平弹簧振子在A、B间做简谐运动,平衡位置为O,已知振子的质量为M。
①简谐运动的能量取决于什么?振子振动时能量如何转化?总的机械能如何变化?
辨析:
A.回复力的方向总是与位移的方向相同。( )
B.回复力的方向总是与加速度的方向相反。( )
C.水平弹簧振子运动到平衡位置时,回复力不为零,能量为零。( )
D.回复力的大小与速度大小无关,速度增大时,回复力可能增大,也可能减小。( )
E.振子在平衡位置,动能最大,弹性势能最小
F.振子在最大位移处,弹性势能最大,动能最小
G.振子在向平衡位置运动时,由于振子振幅减小,故总机械能减小
H.在任意时刻,动能与弹性势能之和保持不变
(2)若振子运动到B处时将一质量为m的物体放到M的上面,且m和M无相对滑动而一起运动,振幅和最大动能如何变化?
12.物理学中,力与运动关系密切,而力的空间积累效果——做功,又是能量转化的量度。因此我们研究某些运动时,可以先分析研究对象的受力特点,进而分析其能量问题。已知重力加速度为,且在下列情境中,均不计空气阻力。
(1)劲度系数为的轻质弹簧上端固定,下端连一可视为质点的小物块,若以小物块的平衡位置为坐标原点,以竖直向下为正方向建立坐标轴,如图所示,用表示小物块由平衡位置向下发生的位移。求小物块的合力与的关系式,并据此说明小物块的运动是否为简谐运动;
(2)系统的总势能为重力势能与弹性势能之和。请你结合小物块的受力特点和求解变力功的基本方法,以平衡位置为系统总势能的零势能参考点,推到小物块振动位移为时系统总势能的表达式。
13.简谐运动是我们研究过的一种典型运动方式。一个质点做机械振动,如果它的回复力与偏离平衡位置的位移大小成正比,而且方向与位移方向相反,就能判定它是简谐运动。如图所示,将两个劲度系数分别为k1和k2的轻质弹簧套在光滑的水平杆上,弹簧的两端固定,中间接一质量为m的小球,此时两弹簧均处于原长。现将小球沿杆拉开一段距离后松开,小球以O为平衡位置往复运动。请你据此证明,小球所做的运动是简谐运动。
14.如图所示,轻弹簧上面固定一质量为m的小球,小球在竖直方向上做简谐运动,振幅为A,运动过程的最高点弹簧正好为原长,则小球在振动过程中,由哪些力提供回复力?平衡位置在哪里?
15.一根弹簧的上端固定,下端系一小球,将小球向下拉一点距离后放手,小球便上下振动起来。试证明这个小球在做简谐运动。(提示:使小球振动的回复力是小球所受到的重力和弹簧弹力的合力)
16.质量为m的小球被劲度系数分别是k1和k2的轻弹簧拴住,置于光滑水平面上,如图所示,此时两个弹簧均处于原长状态,记为位置O。
(1)证明:若将小球在水平方向上拉离位置O再释放,小球将做简谐运动。
(2)已知简谐运动的周期是:,其中k是回复力与位移的比例系数。求出此弹簧振子的周期。
(3)定义:振动物体出现在某区域的时间△t与观察时间t的比值,为振动物体在该区域出现的概率。那么在小球的振动过程中,当观察时间为振动周期的整数倍时,求:小球出现在位置O与右侧0.5A(A为振幅)的区域内的概率P。
试卷第1页,共3页
试卷第1页,共3页
