北京版小学数学四下 7.2平均数 教案
文档属性
| 名称 | 北京版小学数学四下 7.2平均数 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 530.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-16 15:51:36 | ||
图片预览

文档简介
<平均数》教学设计
教学目标:
1.使学生理解平均数的含义,知道平均数的求法。
2.了解平均数在统计学上的意义。
3.学习学习解决生活中有关平均数的问题,增强应用数学知识解决问题的能力。
学习重点;理解平均数的意义,掌握求平均数的方法,
学习难点:理解平均数的意义。
教学准备:多媒体课件,学习单等。
教学过程:
一、创设情境,引入新课。
1.开门见山,板书课题平均数齐读课题,读了课题你有什么问题吗?随机板书:是什么 怎么算 干什么
学校开展了丰富的社团活动,男生和女生正在进行投篮比赛,对于比赛而言你最想知道什么?导入,同学们,我们在以前就学习了数据的收集和整理,学会了用统计图和统计表来表示收到的数据。
二、探究新知。
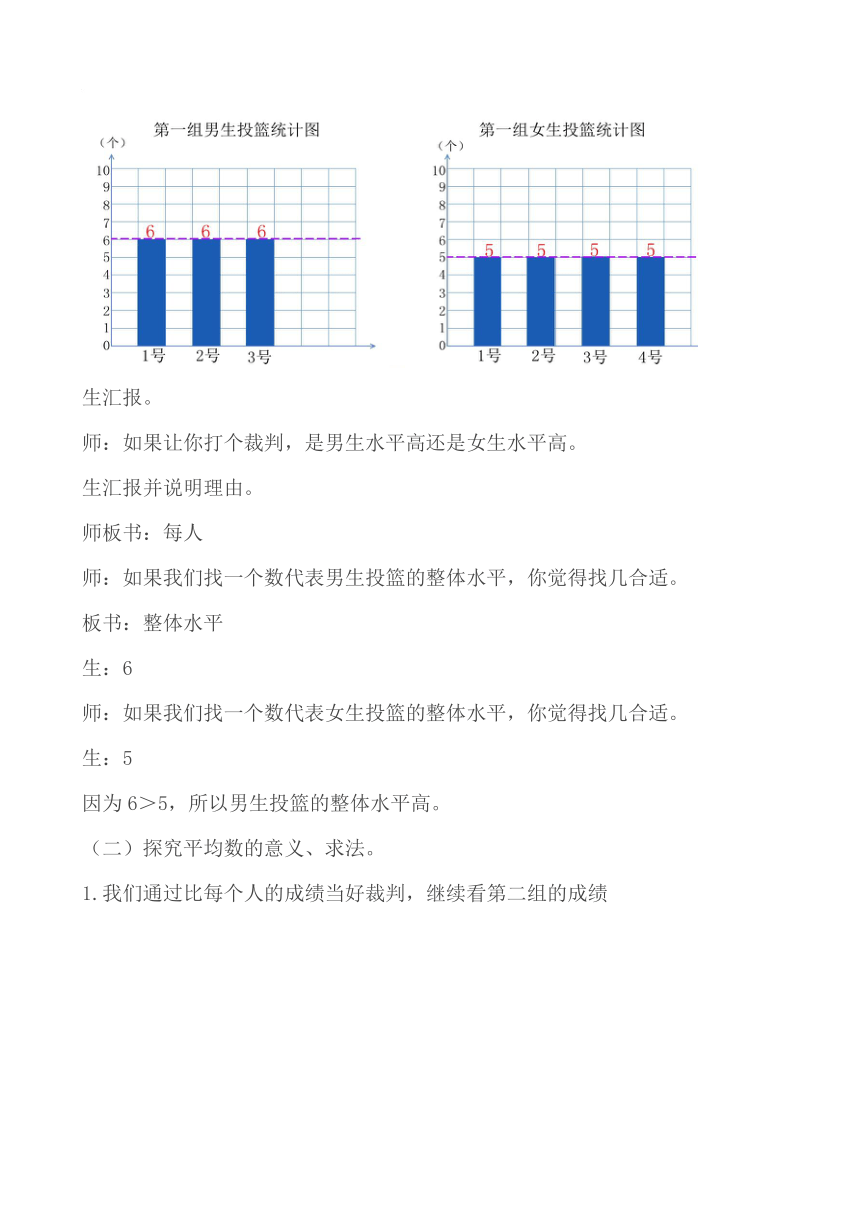
(一)观察这两幅统计图,你知道了什么?
生汇报。
师:如果让你打个裁判,是男生水平高还是女生水平高。
生汇报并说明理由。
师板书:每人
师:如果我们找一个数代表男生投篮的整体水平,你觉得找几合适。
板书:整体水平
生:6
师:如果我们找一个数代表女生投篮的整体水平,你觉得找几合适。
生:5
因为6>5,所以男生投篮的整体水平高。
(二)探究平均数的意义、求法。
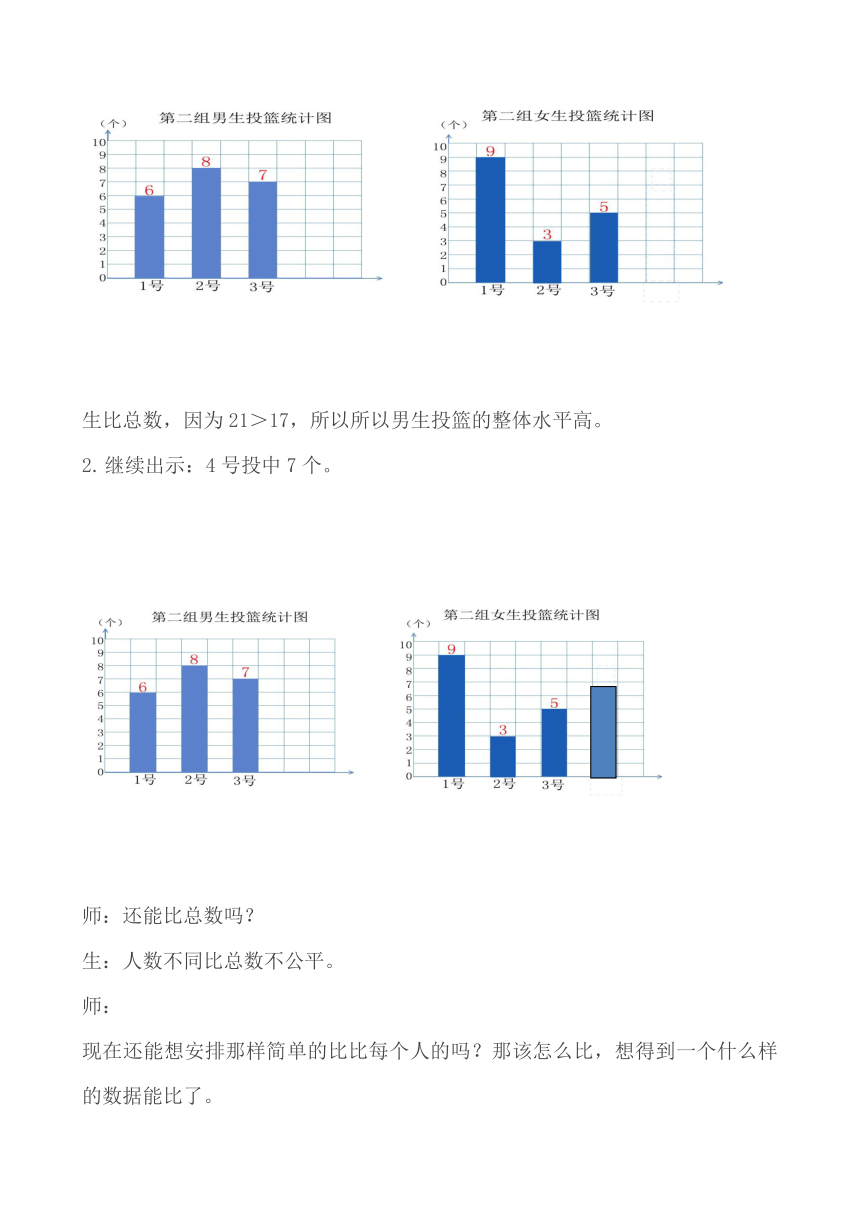
1.我们通过比每个人的成绩当好裁判,继续看第二组的成绩
生比总数,因为21>17,所以所以男生投篮的整体水平高。
继续出示:4号投中7个。
师:还能比总数吗?
生:人数不同比总数不公平。
师:
现在还能想安排那样简单的比比每个人的吗?那该怎么比,想得到一个什么样的数据能比了。
探究学习要求:
1.想一想画一画,或者算一算找出代表男生、女生投篮的整体水平的数。
2.把找出的数用虚线标出来。
3.注意留下思考的痕迹。
生汇报:方法一:移多补少。课件展示。
师:移的目的是什么。
生:把不一样的数变成一样,每人一样。
师:。同学们,想到了用多的补给少的这个方法。使每人投中个数同样多,这种方法在数学上叫做移多补少。
板书:移多补少
师:这里的“6”是他们真实投中的个数吗,那6代表的是什么?
生:代表第二组男生投篮的整体水平,
师:那“7”代表的是什么?
生:代表第二组女生投篮的整体水平,
因为七大于六,所以第二种男生投篮水平高。
还有不同的方法吗?
汇报计算的方法,生板演。并讲解。
其他学生提出问题。小老师解答。
师:给这种方法起名——先合再分。
小结,不管是有移多补少,还是计算的方法,目的是什么?
目的都是要找到一个数,代表他们的整体水平。
师:在数学上把原来几个不相同的数变得同样多,同样多的这个数就叫原来这几个数的平均数。板书:平均数
比如说7是6、8、7的平均数,6是9、3、5、7的平均数.
人数不同比平均数更公平,平均数是一个重要的统计量。
平均属于真实个数比较,。让学生感知平均数是一个虚拟数。
比较两种方法,明确:当数据相差不大,用移多补少方便,当数据相差大,移动麻烦可用计算的方法简便。
出示第三组比赛成绩。
快速猜猜第三组男生投篮成绩。
明确平均数在最小数和最大数之间。
那大家来算一算,这第三组男生投中的平均数。
生计算。
你们看这一号,二号,三号这三人成绩都挺好,怎么平均成绩比三个人都小,这是怎么回事?
生:四号成绩低造成了其他三人成绩有所下降。
明确:平均数受极端数据的影响。
拓展练习
1.在唱歌比赛时,评委打的分为什么要去掉最高分和最低分?你有什么疑问吗?
2.运动会,立定跳远成绩。
姓名成绩次数 1 2 3
聪聪 1.5米 1.8米 1.8米
明明 0.8米 1.9米 1.8米
能去掉最高分和最低分吗?
师:在实际生活中,立定跳远比赛是记录最高成绩的,不算平均数,所以看到一组数据不能全用平均数来表示,而是要根据实际情况灵活选择。
全课小结:说一说你有什么收获。
教学目标:
1.使学生理解平均数的含义,知道平均数的求法。
2.了解平均数在统计学上的意义。
3.学习学习解决生活中有关平均数的问题,增强应用数学知识解决问题的能力。
学习重点;理解平均数的意义,掌握求平均数的方法,
学习难点:理解平均数的意义。
教学准备:多媒体课件,学习单等。
教学过程:
一、创设情境,引入新课。
1.开门见山,板书课题平均数齐读课题,读了课题你有什么问题吗?随机板书:是什么 怎么算 干什么
学校开展了丰富的社团活动,男生和女生正在进行投篮比赛,对于比赛而言你最想知道什么?导入,同学们,我们在以前就学习了数据的收集和整理,学会了用统计图和统计表来表示收到的数据。
二、探究新知。
(一)观察这两幅统计图,你知道了什么?
生汇报。
师:如果让你打个裁判,是男生水平高还是女生水平高。
生汇报并说明理由。
师板书:每人
师:如果我们找一个数代表男生投篮的整体水平,你觉得找几合适。
板书:整体水平
生:6
师:如果我们找一个数代表女生投篮的整体水平,你觉得找几合适。
生:5
因为6>5,所以男生投篮的整体水平高。
(二)探究平均数的意义、求法。
1.我们通过比每个人的成绩当好裁判,继续看第二组的成绩
生比总数,因为21>17,所以所以男生投篮的整体水平高。
继续出示:4号投中7个。
师:还能比总数吗?
生:人数不同比总数不公平。
师:
现在还能想安排那样简单的比比每个人的吗?那该怎么比,想得到一个什么样的数据能比了。
探究学习要求:
1.想一想画一画,或者算一算找出代表男生、女生投篮的整体水平的数。
2.把找出的数用虚线标出来。
3.注意留下思考的痕迹。
生汇报:方法一:移多补少。课件展示。
师:移的目的是什么。
生:把不一样的数变成一样,每人一样。
师:。同学们,想到了用多的补给少的这个方法。使每人投中个数同样多,这种方法在数学上叫做移多补少。
板书:移多补少
师:这里的“6”是他们真实投中的个数吗,那6代表的是什么?
生:代表第二组男生投篮的整体水平,
师:那“7”代表的是什么?
生:代表第二组女生投篮的整体水平,
因为七大于六,所以第二种男生投篮水平高。
还有不同的方法吗?
汇报计算的方法,生板演。并讲解。
其他学生提出问题。小老师解答。
师:给这种方法起名——先合再分。
小结,不管是有移多补少,还是计算的方法,目的是什么?
目的都是要找到一个数,代表他们的整体水平。
师:在数学上把原来几个不相同的数变得同样多,同样多的这个数就叫原来这几个数的平均数。板书:平均数
比如说7是6、8、7的平均数,6是9、3、5、7的平均数.
人数不同比平均数更公平,平均数是一个重要的统计量。
平均属于真实个数比较,。让学生感知平均数是一个虚拟数。
比较两种方法,明确:当数据相差不大,用移多补少方便,当数据相差大,移动麻烦可用计算的方法简便。
出示第三组比赛成绩。
快速猜猜第三组男生投篮成绩。
明确平均数在最小数和最大数之间。
那大家来算一算,这第三组男生投中的平均数。
生计算。
你们看这一号,二号,三号这三人成绩都挺好,怎么平均成绩比三个人都小,这是怎么回事?
生:四号成绩低造成了其他三人成绩有所下降。
明确:平均数受极端数据的影响。
拓展练习
1.在唱歌比赛时,评委打的分为什么要去掉最高分和最低分?你有什么疑问吗?
2.运动会,立定跳远成绩。
姓名成绩次数 1 2 3
聪聪 1.5米 1.8米 1.8米
明明 0.8米 1.9米 1.8米
能去掉最高分和最低分吗?
师:在实际生活中,立定跳远比赛是记录最高成绩的,不算平均数,所以看到一组数据不能全用平均数来表示,而是要根据实际情况灵活选择。
全课小结:说一说你有什么收获。
