1.1.2空间向量的数量积运算 课件(共18张PPT)
文档属性
| 名称 | 1.1.2空间向量的数量积运算 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-17 08:20:22 | ||
图片预览



文档简介
(共18张PPT)
------------------------------------
第一章
空间向量与立体几何
1.2空间向量的数量积运算
空间向量的数量积运算
学习目标
1.掌握两个向量的数量积的概念、性质、计算方法及运算规律
2.能运用数量积求向量夹角和判断向量的共线与垂直.
新课程标准
1.逻辑推理:运用向量运算求距离、夹角;
学习重难点
重点:利用共线向量定理、共面向量定理可以证明一些平行、共面问题;
难点:利用数量积运算可以解决一些距离、夹角问题
知识点一 空间向量数量积的定义
思考1
类比平面向量数量积的定义,给出空间向量数量积的定义.
由于任意两个空间向量都可以通过平移转化为同一平面内的向量,因此,两个空间向量的夹角和数量积就可以像平面向量那样来定义.
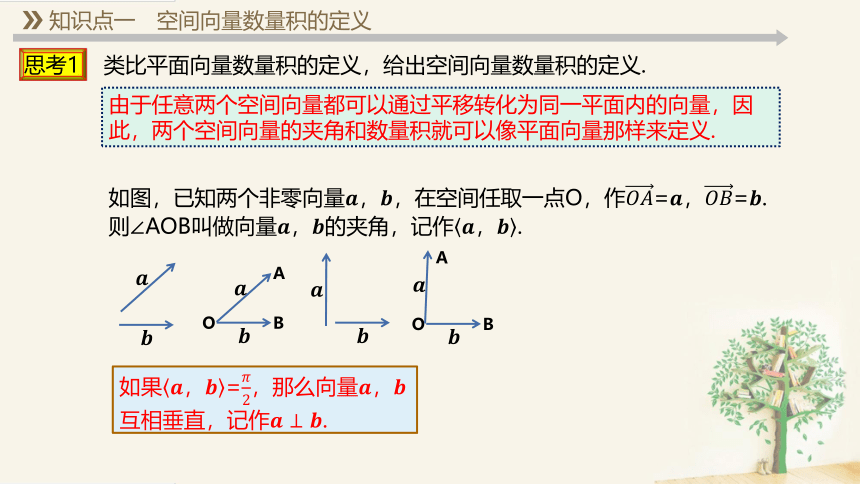
如图,已知两个非零向量,在空间任取一点O,作=,=.
则∠AOB叫做向量的夹角,记作.
O
B
A
O
B
A
如果=,那么向量互相垂直,记作.
知识点一 空间向量数量积的定义
思考1
类比平面向量数量积的定义,给出空间向量数量积的定义.
由于任意两个空间向量都可以通过平移转化为同一平面内的向量,因此,两个空间向量的夹角和数量积就可以像平面向量那样来定义.
已知两个非零向量,则||||cos叫做的数量积,记作. 即
=||||cos
特别地,零向量与任意向量的数量积为0.
由向量的数量积定义,可以得到:
=||||cos=
知识点一 空间向量的投影
思考2
在平面向量的学习中,我们学习了向量的投影.类似地,在空间,向量向向量的投影有什么意义?向量向直线的投影呢?向量向平面β的投影呢?
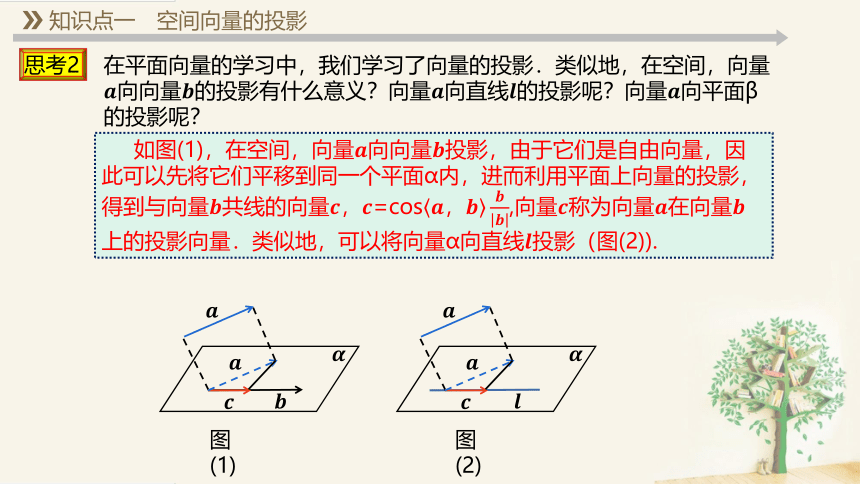
如图(1),在空间,向量向向量投影,由于它们是自由向量,因此可以先将它们平移到同一个平面α内,进而利用平面上向量的投影,得到与向量共线的向量,=cos,向量称为向量在向量上的投影向量.类似地,可以将向量α向直线投影(图(2)).
图(1)
图(2)
知识点一 空间向量的投影
思考2
在平面向量的学习中,我们学习了向量的投影.类似地,在空间,向量向向量的投影有什么意义?向量向直线的投影呢?向量向平面β的投影呢?
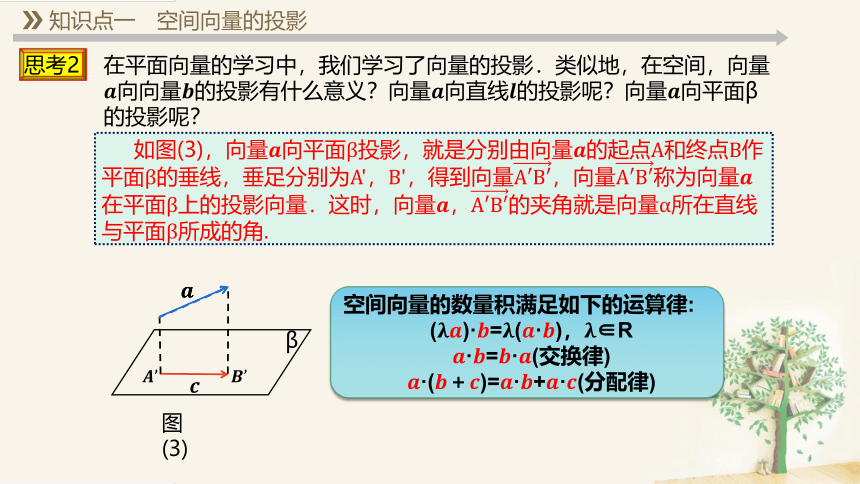
如图(3),向量向平面β投影,就是分别由向量的起点A和终点B作平面β的垂线,垂足分别为A',B',得到向量,向量称为向量在平面β上的投影向量.这时,向量,的夹角就是向量α所在直线与平面β所成的角.
β
图(3)
空间向量的数量积满足如下的运算律:
()·=(·),∈R
·=·(交换律)
·(+)=·+·(分配律)
知识点一 空间向量的投影
思考3
对于三个均不为0的数a,b,c,若ab=ac,则b=c.对于向量,,,由=,你能得到=吗 如果不能,请举出反例.
解析:不能得到=,即向量不能约分.
例:如图,在三棱锥S-ABC中,SC平面ABC, SCAC,SCBC,设=,=, =,则==0,但
思考4
对于三个均不为0的数a,b、c ,若ab=c,则a=(或b=).对于向量,,若=k,能不能写成(或)的形式
解析:=k,不能写成(或)的形式,即向量没有除法运算
知识点一 空间向量的投影
思考5
对于三个均不为0的数a,b,c,有(ab )c =a(bc).
对于向量,,,()=()成立吗 为什么
解析:对于向量,,,()=()不成立,也就是说,向量的数量积不满足结合律.
如:任意取三个不共面的向量,其中不共线,()是一个数与向量作数乘, (·)是一个数与向量作数乘,而向量,不共线所以(-) 与(·)不相等
例题精讲 ——例一
例1.已知平行六面体ABCD﹣A’B’C’D’中,AB=5,AD=3,AA′=7, ∠BAD=60°,∠BAA′=∠DAA′=45°,
(1)求的长;
(2)求AC’的长(精确到0.1).
例题精讲 ——例一
例1.已知平行六面体ABCD﹣A’B’C’D’中,AB=5,AD=3,AA′=7, ∠BAD=60°,∠BAA′=∠DAA′=45°,
(1)求的长;
(2)求AC’的长(精确到0.1).
解析:(1)·=||| cos
=5×3×cos 60°=7.5;
(2)=(++)
=+++2(·+·+·)
=+++2(5×3×cos 60°+5×7×cos45° +3×7×cos 45°)
=98+56,
所以AC'13.3.
由于空间向量的线性运算和数量积运算具有鲜明的几何背景,空间图形的许多性质可以由向量的线性运算及数量积运算表示出来,因此,立体几何中的许多问题可以用向量运算的方法加以解决.
例题精讲 ——变式练习1
已知平行六面体ABCD﹣A’B’C’D’中,AB=4,AD=3,AA′=5, ∠BAD=90°,∠BAA′=∠DAA′=60°,
(1);(2)求AB’的长;
(3)求AC’的长.
例题精讲 ——变式练习1
已知平行六面体ABCD﹣A’B’C’D’中,AB=4,AD=3,AA′=5, ∠BAD=90°,∠BAA′=∠DAA′=60°,
(1);(2)求AB’的长;
(3)求AC’的长.
解析:(1)·=||| cos<,>=5×4×cos 60°=10;
(2)因为=+
||===
(3)因为=5×3×cos 60°=,=3×4×cos 90°=0
所以=(++)
=+++2(·+·+·)
=+++2(0+10+)=85=.
例题精讲 ——例二
如图,m,n是平面α内的两条相交直线.如果,,求证:平面α.
分析:要证明平面α,就是要证明l垂直于α内的任意一条直线g(直线与平面垂直的定义).如果我们能在g和m,n之间建立某种联系,并由,,得到,那么就能解决此问题.
例题精讲 ——例二
如图,m,n是平面α内的两条相交直线.如果,,求证:平面α.
证明:在平面α内作任意一条直线,分别在直线
, , 上取非零向量,, , .
因为直线与相交,所以向量, ,不平行.由向量共面的充要条件可知,存在唯一的有序实效对(,),使
=.
将上式两边分别与向量作数量积运算,得
=,
因为=0,=0(为什么 ),所以 =0.所以.
这就证明了直线垂直于平面α内的任意一条直线,所以平面α.
课堂检测
1.如图,在正三棱柱ABC-A1B1C1中,若AB=BB1,则AB1与
BC1,所成角的大小为( ).
(A) 60° (B) 90° (C) 105° (D) 75°
解析:设 BB1= 1,则AB = ,
= ,
==,
= ()(+)
=2
= 1× ×cos 60° =0,
,AB1BC1.
AB1与BC1,所成角的大小为90,故选B.
B
课堂检测
2.如图,正方体 ABCD -A'B'CD'的棱长为1,设=a, =b,=c,求:
(1)a·(b+c);
(2) a·(a+b+c);
(3) (a+b)·(b+c).
解析:(1)a ·( b+c)= a · b+a · c =0.
(2)a · ( a+b+c)= a · a+a · b+a · c= 1.
(3)(a+b)·(b+c)= a · b+a · c+b · b+b· c= 1.
课堂检测
3.如图,线段AB,BD在平面α内,BDAB,AC,且 AB=a,BD=b,AC=c. 求C,D两点间的距离.
解析:=++
=+2+2+2
=
即C,D两点间的距离为
课堂小结
空间向量的数量积
已知两个非零向量,则||||cos叫做的数量积,记作. 即
=||||cos
------------------------------------
第一章
空间向量与立体几何
1.2空间向量的数量积运算
空间向量的数量积运算
学习目标
1.掌握两个向量的数量积的概念、性质、计算方法及运算规律
2.能运用数量积求向量夹角和判断向量的共线与垂直.
新课程标准
1.逻辑推理:运用向量运算求距离、夹角;
学习重难点
重点:利用共线向量定理、共面向量定理可以证明一些平行、共面问题;
难点:利用数量积运算可以解决一些距离、夹角问题
知识点一 空间向量数量积的定义
思考1
类比平面向量数量积的定义,给出空间向量数量积的定义.
由于任意两个空间向量都可以通过平移转化为同一平面内的向量,因此,两个空间向量的夹角和数量积就可以像平面向量那样来定义.
如图,已知两个非零向量,在空间任取一点O,作=,=.
则∠AOB叫做向量的夹角,记作.
O
B
A
O
B
A
如果=,那么向量互相垂直,记作.
知识点一 空间向量数量积的定义
思考1
类比平面向量数量积的定义,给出空间向量数量积的定义.
由于任意两个空间向量都可以通过平移转化为同一平面内的向量,因此,两个空间向量的夹角和数量积就可以像平面向量那样来定义.
已知两个非零向量,则||||cos叫做的数量积,记作. 即
=||||cos
特别地,零向量与任意向量的数量积为0.
由向量的数量积定义,可以得到:
=||||cos=
知识点一 空间向量的投影
思考2
在平面向量的学习中,我们学习了向量的投影.类似地,在空间,向量向向量的投影有什么意义?向量向直线的投影呢?向量向平面β的投影呢?
如图(1),在空间,向量向向量投影,由于它们是自由向量,因此可以先将它们平移到同一个平面α内,进而利用平面上向量的投影,得到与向量共线的向量,=cos,向量称为向量在向量上的投影向量.类似地,可以将向量α向直线投影(图(2)).
图(1)
图(2)
知识点一 空间向量的投影
思考2
在平面向量的学习中,我们学习了向量的投影.类似地,在空间,向量向向量的投影有什么意义?向量向直线的投影呢?向量向平面β的投影呢?
如图(3),向量向平面β投影,就是分别由向量的起点A和终点B作平面β的垂线,垂足分别为A',B',得到向量,向量称为向量在平面β上的投影向量.这时,向量,的夹角就是向量α所在直线与平面β所成的角.
β
图(3)
空间向量的数量积满足如下的运算律:
()·=(·),∈R
·=·(交换律)
·(+)=·+·(分配律)
知识点一 空间向量的投影
思考3
对于三个均不为0的数a,b,c,若ab=ac,则b=c.对于向量,,,由=,你能得到=吗 如果不能,请举出反例.
解析:不能得到=,即向量不能约分.
例:如图,在三棱锥S-ABC中,SC平面ABC, SCAC,SCBC,设=,=, =,则==0,但
思考4
对于三个均不为0的数a,b、c ,若ab=c,则a=(或b=).对于向量,,若=k,能不能写成(或)的形式
解析:=k,不能写成(或)的形式,即向量没有除法运算
知识点一 空间向量的投影
思考5
对于三个均不为0的数a,b,c,有(ab )c =a(bc).
对于向量,,,()=()成立吗 为什么
解析:对于向量,,,()=()不成立,也就是说,向量的数量积不满足结合律.
如:任意取三个不共面的向量,其中不共线,()是一个数与向量作数乘, (·)是一个数与向量作数乘,而向量,不共线所以(-) 与(·)不相等
例题精讲 ——例一
例1.已知平行六面体ABCD﹣A’B’C’D’中,AB=5,AD=3,AA′=7, ∠BAD=60°,∠BAA′=∠DAA′=45°,
(1)求的长;
(2)求AC’的长(精确到0.1).
例题精讲 ——例一
例1.已知平行六面体ABCD﹣A’B’C’D’中,AB=5,AD=3,AA′=7, ∠BAD=60°,∠BAA′=∠DAA′=45°,
(1)求的长;
(2)求AC’的长(精确到0.1).
解析:(1)·=||| cos
=5×3×cos 60°=7.5;
(2)=(++)
=+++2(·+·+·)
=+++2(5×3×cos 60°+5×7×cos45° +3×7×cos 45°)
=98+56,
所以AC'13.3.
由于空间向量的线性运算和数量积运算具有鲜明的几何背景,空间图形的许多性质可以由向量的线性运算及数量积运算表示出来,因此,立体几何中的许多问题可以用向量运算的方法加以解决.
例题精讲 ——变式练习1
已知平行六面体ABCD﹣A’B’C’D’中,AB=4,AD=3,AA′=5, ∠BAD=90°,∠BAA′=∠DAA′=60°,
(1);(2)求AB’的长;
(3)求AC’的长.
例题精讲 ——变式练习1
已知平行六面体ABCD﹣A’B’C’D’中,AB=4,AD=3,AA′=5, ∠BAD=90°,∠BAA′=∠DAA′=60°,
(1);(2)求AB’的长;
(3)求AC’的长.
解析:(1)·=||| cos<,>=5×4×cos 60°=10;
(2)因为=+
||===
(3)因为=5×3×cos 60°=,=3×4×cos 90°=0
所以=(++)
=+++2(·+·+·)
=+++2(0+10+)=85=.
例题精讲 ——例二
如图,m,n是平面α内的两条相交直线.如果,,求证:平面α.
分析:要证明平面α,就是要证明l垂直于α内的任意一条直线g(直线与平面垂直的定义).如果我们能在g和m,n之间建立某种联系,并由,,得到,那么就能解决此问题.
例题精讲 ——例二
如图,m,n是平面α内的两条相交直线.如果,,求证:平面α.
证明:在平面α内作任意一条直线,分别在直线
, , 上取非零向量,, , .
因为直线与相交,所以向量, ,不平行.由向量共面的充要条件可知,存在唯一的有序实效对(,),使
=.
将上式两边分别与向量作数量积运算,得
=,
因为=0,=0(为什么 ),所以 =0.所以.
这就证明了直线垂直于平面α内的任意一条直线,所以平面α.
课堂检测
1.如图,在正三棱柱ABC-A1B1C1中,若AB=BB1,则AB1与
BC1,所成角的大小为( ).
(A) 60° (B) 90° (C) 105° (D) 75°
解析:设 BB1= 1,则AB = ,
= ,
==,
= ()(+)
=2
= 1× ×cos 60° =0,
,AB1BC1.
AB1与BC1,所成角的大小为90,故选B.
B
课堂检测
2.如图,正方体 ABCD -A'B'CD'的棱长为1,设=a, =b,=c,求:
(1)a·(b+c);
(2) a·(a+b+c);
(3) (a+b)·(b+c).
解析:(1)a ·( b+c)= a · b+a · c =0.
(2)a · ( a+b+c)= a · a+a · b+a · c= 1.
(3)(a+b)·(b+c)= a · b+a · c+b · b+b· c= 1.
课堂检测
3.如图,线段AB,BD在平面α内,BDAB,AC,且 AB=a,BD=b,AC=c. 求C,D两点间的距离.
解析:=++
=+2+2+2
=
即C,D两点间的距离为
课堂小结
空间向量的数量积
已知两个非零向量,则||||cos叫做的数量积,记作. 即
=||||cos
