1.2空间向量基本定理 课件(共21张PPT)
文档属性
| 名称 | 1.2空间向量基本定理 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-17 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
------------------------------------
第一章
空间向量与立体几何
1.2空间向量基本定理
空间向量基本定理
学习目标
认识空间向量基本定理,理解空间向量正交分解。
学习重难点
重点:空间基底表示已知向量
难点:空间基底表示已知向量
知识点一 空间向量基本定理
我们所在的教室即是一个三维立体图,如果以教室的一个墙角为始点,沿着三条墙缝作向量可以得到三个空间向量.这三个空间向量是不共面的
那么能否用这三个向量表示空间中任意的向量呢?
空间中任意向量怎么表示?
向量
空间向量基本定理
如图, 设是空间中三个两两垂直的向量,且表示他们的有向线段有公共起点o,对于任意一个空间向量,设为在所确定的平面上的投影向量,则=+,又向量,共线,因此存在唯一实数z,使得,从而
=+z ,
而在所确定的平面上,由平面向量基本定理可知,存在唯一的有序实数对(x,y),使得
=x+y .
从而,=+z = x+y+z .
因此,如果是空间三个两两垂直的向量,那么对于任意一个空间向量存在唯一有序实数组(x,y,z),使得
=x+y+z .
我们称x,y,z分别为向量在上的分向量。
1
探究
在空间中,如果用任意三个不共面的向量,代替两两垂直的向量你能得出类似的结论吗
空间向量基本定理
定理:如果三个向量不共面,那么对任意一个空间向量,存在唯一的有序实数组(),使得=++.
我们把定理中的叫做空间的一个基底,都叫做基向量.空间任意三个不共面的向量都可以构成空间的一个基底.
如果空间的一个基底中的三个基向量两两垂直,且长度都为1,那么这个基底叫做单位正交基底,常用表示.
由空间向量基本定理可知,对空间中的任意向量,均可以分解为三个向量,使=,像这样,把一个空间向量分解为三个两两垂直的向量,叫做把空间向量进行正交分解.
空间向量基本定理
定理辨析
1.空间任意三个不共面的向量都可构成空间的一个基底.基底选定后,空间的所有向量均可由基底唯一表示;不同基底下,同一向量的表达式也有可能不同.
2.一个基底是一个向量组,一个基向量是指基底中的某一个向量,二者是相关联的不同概念.
3.由于零向量与任意一个非零向量共线,与任意两个不共线的非零向量共面,所以若三个向量不共面,就说明它们都不是零向量.
做一做
1.判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)空间向量的基底是唯一的.( )
(2)若是空间向量的一个基底,则均为非零向量.( )
(3)已知A,B,M,N是空间四点,若, , 不能构成空间的一个基底,则A,B,M,N共面.( )
(4)若{}是空间的一个基底,且存在实数x,y,z使得=0,则有x=y=z=0.( )
做一做
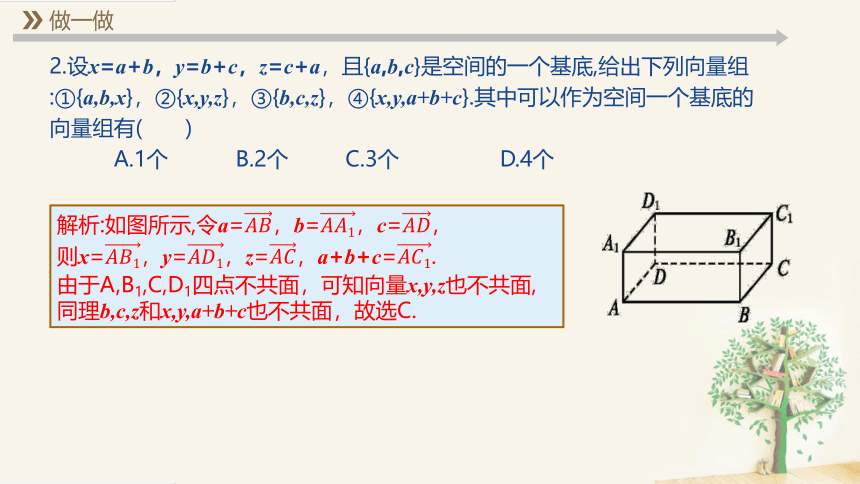
2.设x=a+b,y=b+c,z=c+a,且{a,b,c}是空间的一个基底,给出下列向量组:①{a,b,x},②{x,y,z},③{b,c,z},④{x,y,a+b+c}.其中可以作为空间一个基底的向量组有( )
A.1个 B.2个 C.3个 D.4个
解析:如图所示,令a=,b=,c=,
则x=,y=,z=,a+b+c=.
由于A,B1,C,D1四点不共面,可知向量x,y,z也不共面,
同理b,c,z和x,y,a+b+c也不共面,故选C.
例题精讲 ——例1
(1)设向量a,b,c不共面,则下列集合(集合中元素都是向量,手写体必须添加箭头)可作为空间的一个基底的是( )
A.{a-2b,3a-b,0} B.{a,b,a+b}
C.{3a+b,a+b,c} D.{a+b+c,a+b,c}
解析(1)基底满足三个向量不共面,即a + b +c= 0 ,当且仅当===0,
A.令(a-2b) + (3a - b)+0 =0,能推出a ,b,与0共面,故A不满足;
Ba+ b+(a+b)=0,能推出a ,b与a+b共线,故B不满足;
C.( 3a+b)+ (a+b)+c=0 ,,三个向量不共面,故C满足;
D.( a+b+c) +(a+b)+c=0,只需=或入=-,故D不满足.
故选C.
C
例题精讲 ——例1
(2)已知{e1,e2,e3}是空间的一个基底,且=e1+2e2-e3,=-3e1+e2+2e3,=e1+e2-e3,试判断{,,}能否作为空间的一个基底?
解析(2)假设,,共面,设=x+y
e1+2e2-e3=x(-3e1+e2+2e3)+y(e1+e2-e3)
=(-3x+y)e1+(x+y)e2+(2x-y)e3
{e1,e2,e3}是空间的一个基底,e1,e2,e3不共面
,方程无解,
故,,能作为空间的一个基底
例题精讲 ——变式练习1
已知向量{a,b,c}是空间的一个基底,从a,b,c中选哪一个向量,一定可以与向量p=ab,q=ab构成空间的另一个基底
解析:向量a, b ,c是空间的一个基底,
a, b ,c不共面.
ab,ab ,c也不共面,
p,q,c可做为空间的一个基底.
例题精讲 ——例2
如图,M是四面体(OABC的棱BC的中点,点N在线段OM上,点P在线段AN上,且MN=ON,AP=AN,用向量,,表示.
分析:,,,是三个不共面的向量,它们构成空间的一-个基底{,,},可以用基底{,,}表示出来.
解析:(1)
例题精讲 ——变式练习2
如图,已知平行六面体OABC-O'A'B'C',点G是侧面BB'C'C的中心,且=a,=b,=c.
(1) {a, b ,c}是否构成空间的一个基底
(2) 如果{a, b ,c}构成空间的一个基底,那么用它表示下列向量:,,,
解析:(1)因为a,b,c己不共面,所以{a,b,c}可以构成空间的一个基底;
(2)=+ = a+b
= += += cb
=++=++= ab+c
=+=+=+( +)
=+(+) =c
例题精讲 ——例3
已知平行六面体ABCD﹣A1B1C1D1中,AB=4,AD=4,AA1=5, ∠BAD=60°,∠BAA1=60°,∠DAA1=60°,M、 N分别为D1C1,C1B1的中点. 求证MNAC.
M
N
解析:要证MNAC,只需证明·=0.由已知,{,,}可构成空问的一个基底.把 和分别用基底表示,然后计算·即可.
例题精讲 ——例3
已知平行六面体ABCD﹣A1B1C1D1中,AB=4,AD=4,AA1=5, ∠BAD=60°,∠BAA1=60°,∠DAA1=60°,M、 N分别为D1C1,C1B1的中点. 求证MNAC.
解析:证明:设 这三个向量不共面,{, }构成空间的一个基底,我们用它们表示,则
所以
=
=
所以
M
N
例题精讲 ——例4
如图,正方体ABCD -A'B'C'D'的棱长为1,E,F,G分别为C'D',A'D',D'D的中点.
(1)求证:EF//AC;
(2)求CE与AG所成角的余弦值.
如图,正方体ABCD -A'B'C'D'的棱长为1,E,F,G分别为C'D',A'D',D'D的中点.
(1)求证:EF//AC;
(2)求CE与AG所成角的余弦值.
分析:(1)要证明EF//AC,只需证明与共线.设=,=, =,则{ ,, }构成空间的一个单位正交基底,把和分别用基向量表示,作相应的运算证明它们共线即可.
(2)要求CE与AG所成角的余弦值,只需求,所成角的余弦值即可.
例题精讲 ——例4
已知平行六面体ABCD﹣A1B1C1D1中,AB=4,AD=4,AA1=5, ∠BAD=60°,∠BAA1=60°,∠DAA1=60°,M、 N分别为D1C1,C1B1的中点. 求证MNAC.
解析:(1):设=,=,=,则{,,}构成空间的一个单位正交基底.所以
=-=-=(-),=-=-.
所以=.
所以EF//AC.
(2)因为=+=-+,
=+=-+
所以==
所以CE与AG所成角的余弦值为.
课堂检测
1.已知四面体OABC,OB=OC,AOB=AOC=.
求证OABC.
证明:因为OB = OC,所以
所以
所以,所以.
课堂检测
2.如图,在平行六面体 ABCD -A'B'C'D'中, AB=2, AD=2, AA'=3,BAD=BAA'=DAA'=60°
求BC'与CA'所成角的余弦值.
解析:设= a , =b , =c,因为这三个向量不共面,所以{a,b,c}构成空间的一个基底.
则=+ =+=b+c ,
=== ab+c ,
所以= (b+c)·(ab+c)= a·bb·bb·ca·c b·c + c·c
= 2×2× 22+2×3× 2×3× 2×3×+32=0
所以==0.
所以BC'与CA'所成角的余弦值为0.
课堂检测
3.如图,已知正方体 ABCD -A'B'C'D', CD'和DC'相交于点O,连接AO,求证AOCD'.
解析:设= a , =b , =c,则{a,b,c}可以构成空间的一个基底;所以
==a+b+c
=a+c
所以=(a+b+c)(a+c)
=aa+acab+bc-ac+c=0
所以AOCD
课堂小结
空间向量
1.利用向量的线性运算和空间向量基本定理表示向量是向量应用的基础.
2.利用共线向量定理、共面向量定理可以证明一些平行、共面问题;利用数量积运算可以解决一些距离、夹角问题.
3.利用向量解立体几何题的一般方法:把线段或角度转化为向量表示,用已知向量表示未知向量,然后通过向量的运算或证明去解决问题.其中合理选取基底是优化运算的关键.
1
2
3
------------------------------------
第一章
空间向量与立体几何
1.2空间向量基本定理
空间向量基本定理
学习目标
认识空间向量基本定理,理解空间向量正交分解。
学习重难点
重点:空间基底表示已知向量
难点:空间基底表示已知向量
知识点一 空间向量基本定理
我们所在的教室即是一个三维立体图,如果以教室的一个墙角为始点,沿着三条墙缝作向量可以得到三个空间向量.这三个空间向量是不共面的
那么能否用这三个向量表示空间中任意的向量呢?
空间中任意向量怎么表示?
向量
空间向量基本定理
如图, 设是空间中三个两两垂直的向量,且表示他们的有向线段有公共起点o,对于任意一个空间向量,设为在所确定的平面上的投影向量,则=+,又向量,共线,因此存在唯一实数z,使得,从而
=+z ,
而在所确定的平面上,由平面向量基本定理可知,存在唯一的有序实数对(x,y),使得
=x+y .
从而,=+z = x+y+z .
因此,如果是空间三个两两垂直的向量,那么对于任意一个空间向量存在唯一有序实数组(x,y,z),使得
=x+y+z .
我们称x,y,z分别为向量在上的分向量。
1
探究
在空间中,如果用任意三个不共面的向量,代替两两垂直的向量你能得出类似的结论吗
空间向量基本定理
定理:如果三个向量不共面,那么对任意一个空间向量,存在唯一的有序实数组(),使得=++.
我们把定理中的叫做空间的一个基底,都叫做基向量.空间任意三个不共面的向量都可以构成空间的一个基底.
如果空间的一个基底中的三个基向量两两垂直,且长度都为1,那么这个基底叫做单位正交基底,常用表示.
由空间向量基本定理可知,对空间中的任意向量,均可以分解为三个向量,使=,像这样,把一个空间向量分解为三个两两垂直的向量,叫做把空间向量进行正交分解.
空间向量基本定理
定理辨析
1.空间任意三个不共面的向量都可构成空间的一个基底.基底选定后,空间的所有向量均可由基底唯一表示;不同基底下,同一向量的表达式也有可能不同.
2.一个基底是一个向量组,一个基向量是指基底中的某一个向量,二者是相关联的不同概念.
3.由于零向量与任意一个非零向量共线,与任意两个不共线的非零向量共面,所以若三个向量不共面,就说明它们都不是零向量.
做一做
1.判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)空间向量的基底是唯一的.( )
(2)若是空间向量的一个基底,则均为非零向量.( )
(3)已知A,B,M,N是空间四点,若, , 不能构成空间的一个基底,则A,B,M,N共面.( )
(4)若{}是空间的一个基底,且存在实数x,y,z使得=0,则有x=y=z=0.( )
做一做
2.设x=a+b,y=b+c,z=c+a,且{a,b,c}是空间的一个基底,给出下列向量组:①{a,b,x},②{x,y,z},③{b,c,z},④{x,y,a+b+c}.其中可以作为空间一个基底的向量组有( )
A.1个 B.2个 C.3个 D.4个
解析:如图所示,令a=,b=,c=,
则x=,y=,z=,a+b+c=.
由于A,B1,C,D1四点不共面,可知向量x,y,z也不共面,
同理b,c,z和x,y,a+b+c也不共面,故选C.
例题精讲 ——例1
(1)设向量a,b,c不共面,则下列集合(集合中元素都是向量,手写体必须添加箭头)可作为空间的一个基底的是( )
A.{a-2b,3a-b,0} B.{a,b,a+b}
C.{3a+b,a+b,c} D.{a+b+c,a+b,c}
解析(1)基底满足三个向量不共面,即a + b +c= 0 ,当且仅当===0,
A.令(a-2b) + (3a - b)+0 =0,能推出a ,b,与0共面,故A不满足;
Ba+ b+(a+b)=0,能推出a ,b与a+b共线,故B不满足;
C.( 3a+b)+ (a+b)+c=0 ,,三个向量不共面,故C满足;
D.( a+b+c) +(a+b)+c=0,只需=或入=-,故D不满足.
故选C.
C
例题精讲 ——例1
(2)已知{e1,e2,e3}是空间的一个基底,且=e1+2e2-e3,=-3e1+e2+2e3,=e1+e2-e3,试判断{,,}能否作为空间的一个基底?
解析(2)假设,,共面,设=x+y
e1+2e2-e3=x(-3e1+e2+2e3)+y(e1+e2-e3)
=(-3x+y)e1+(x+y)e2+(2x-y)e3
{e1,e2,e3}是空间的一个基底,e1,e2,e3不共面
,方程无解,
故,,能作为空间的一个基底
例题精讲 ——变式练习1
已知向量{a,b,c}是空间的一个基底,从a,b,c中选哪一个向量,一定可以与向量p=ab,q=ab构成空间的另一个基底
解析:向量a, b ,c是空间的一个基底,
a, b ,c不共面.
ab,ab ,c也不共面,
p,q,c可做为空间的一个基底.
例题精讲 ——例2
如图,M是四面体(OABC的棱BC的中点,点N在线段OM上,点P在线段AN上,且MN=ON,AP=AN,用向量,,表示.
分析:,,,是三个不共面的向量,它们构成空间的一-个基底{,,},可以用基底{,,}表示出来.
解析:(1)
例题精讲 ——变式练习2
如图,已知平行六面体OABC-O'A'B'C',点G是侧面BB'C'C的中心,且=a,=b,=c.
(1) {a, b ,c}是否构成空间的一个基底
(2) 如果{a, b ,c}构成空间的一个基底,那么用它表示下列向量:,,,
解析:(1)因为a,b,c己不共面,所以{a,b,c}可以构成空间的一个基底;
(2)=+ = a+b
= += += cb
=++=++= ab+c
=+=+=+( +)
=+(+) =c
例题精讲 ——例3
已知平行六面体ABCD﹣A1B1C1D1中,AB=4,AD=4,AA1=5, ∠BAD=60°,∠BAA1=60°,∠DAA1=60°,M、 N分别为D1C1,C1B1的中点. 求证MNAC.
M
N
解析:要证MNAC,只需证明·=0.由已知,{,,}可构成空问的一个基底.把 和分别用基底表示,然后计算·即可.
例题精讲 ——例3
已知平行六面体ABCD﹣A1B1C1D1中,AB=4,AD=4,AA1=5, ∠BAD=60°,∠BAA1=60°,∠DAA1=60°,M、 N分别为D1C1,C1B1的中点. 求证MNAC.
解析:证明:设 这三个向量不共面,{, }构成空间的一个基底,我们用它们表示,则
所以
=
=
所以
M
N
例题精讲 ——例4
如图,正方体ABCD -A'B'C'D'的棱长为1,E,F,G分别为C'D',A'D',D'D的中点.
(1)求证:EF//AC;
(2)求CE与AG所成角的余弦值.
如图,正方体ABCD -A'B'C'D'的棱长为1,E,F,G分别为C'D',A'D',D'D的中点.
(1)求证:EF//AC;
(2)求CE与AG所成角的余弦值.
分析:(1)要证明EF//AC,只需证明与共线.设=,=, =,则{ ,, }构成空间的一个单位正交基底,把和分别用基向量表示,作相应的运算证明它们共线即可.
(2)要求CE与AG所成角的余弦值,只需求,所成角的余弦值即可.
例题精讲 ——例4
已知平行六面体ABCD﹣A1B1C1D1中,AB=4,AD=4,AA1=5, ∠BAD=60°,∠BAA1=60°,∠DAA1=60°,M、 N分别为D1C1,C1B1的中点. 求证MNAC.
解析:(1):设=,=,=,则{,,}构成空间的一个单位正交基底.所以
=-=-=(-),=-=-.
所以=.
所以EF//AC.
(2)因为=+=-+,
=+=-+
所以==
所以CE与AG所成角的余弦值为.
课堂检测
1.已知四面体OABC,OB=OC,AOB=AOC=.
求证OABC.
证明:因为OB = OC,所以
所以
所以,所以.
课堂检测
2.如图,在平行六面体 ABCD -A'B'C'D'中, AB=2, AD=2, AA'=3,BAD=BAA'=DAA'=60°
求BC'与CA'所成角的余弦值.
解析:设= a , =b , =c,因为这三个向量不共面,所以{a,b,c}构成空间的一个基底.
则=+ =+=b+c ,
=== ab+c ,
所以= (b+c)·(ab+c)= a·bb·bb·ca·c b·c + c·c
= 2×2× 22+2×3× 2×3× 2×3×+32=0
所以==0.
所以BC'与CA'所成角的余弦值为0.
课堂检测
3.如图,已知正方体 ABCD -A'B'C'D', CD'和DC'相交于点O,连接AO,求证AOCD'.
解析:设= a , =b , =c,则{a,b,c}可以构成空间的一个基底;所以
==a+b+c
=a+c
所以=(a+b+c)(a+c)
=aa+acab+bc-ac+c=0
所以AOCD
课堂小结
空间向量
1.利用向量的线性运算和空间向量基本定理表示向量是向量应用的基础.
2.利用共线向量定理、共面向量定理可以证明一些平行、共面问题;利用数量积运算可以解决一些距离、夹角问题.
3.利用向量解立体几何题的一般方法:把线段或角度转化为向量表示,用已知向量表示未知向量,然后通过向量的运算或证明去解决问题.其中合理选取基底是优化运算的关键.
1
2
3
