( 精品 )2022人教版小学数学六年级下册第4单元4.2正比例和反比例同步练习(含解析)
文档属性
| 名称 | ( 精品 )2022人教版小学数学六年级下册第4单元4.2正比例和反比例同步练习(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-16 22:03:17 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2022人教版小学数学六年级下册
第4单元 4.2正比例和反比例 同步练习
一、单选题
1.表示a、b成正比例关系的是( )
A.a+b= B.ab= C.a= b
2.下面所给例子中( )不成比例
A.速度一定时,路程和所用时间 B.单价一定时,数量和总价
C.长方形的面积和宽 D.圆锥底面积一定时,体积和高
3.全班人数一定,出勤人数和出勤率( )比例。
A.成正 B.成反 C.不成
4.今年妈妈的年龄是儿子的3倍,儿子年龄和妈妈的年龄( )
A.成正比例 B.成反比例 C.不成比例 D.无法判断
5.用比例解.
某厂原计划4月份生产化肥100吨,实际前5天就生产了23吨.照这样计算,这个月可以超额生产( )
A.28吨 B.38吨 C.83吨 D.50吨
二、判断题
6.小海跳高的高度和他的身高成正比例。( )
7.一个非零自然数与它的倒数成反比例关系。( )
8.圆的周长和面积成正比例。( )
9.两种量不成正比例就成反比例。( )
10.圆锥的高一定,圆锥的体积和底面积成正比例。( )
11.正方体的体积与棱长成正比例。( )
三、填空题
12.下表中,如果x和y成正比例,?"处填 ;如果x和y成反比例,“?“处填 。
x 4
y 12 24
13.一辆货车每次运煤的吨数一定,运煤的总量和运的次数 (成正比例、不成比例)
14.用数学的眼光来看成语“立竿见影”,是应用了本学期所学的 知识。即同一时间,同一地点,竿高和影长成 比例。
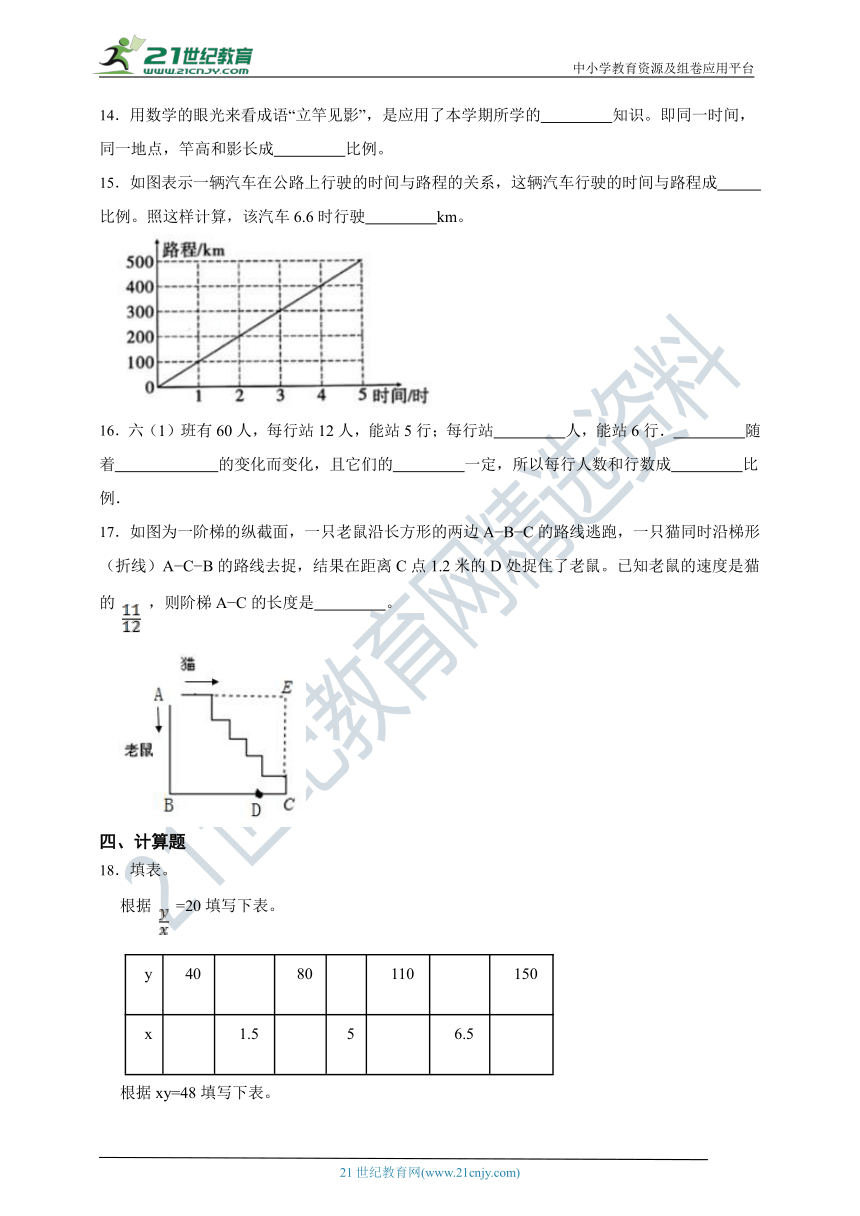
15.如图表示一辆汽车在公路上行驶的时间与路程的关系,这辆汽车行驶的时间与路程成 比例。照这样计算,该汽车6.6时行驶 km。
16.六(1)班有60人,每行站12人,能站5行;每行站 人,能站6行. 随着 的变化而变化,且它们的 一定,所以每行人数和行数成 比例.
17.如图为一阶梯的纵截面,一只老鼠沿长方形的两边A B C的路线逃跑,一只猫同时沿梯形(折线)A C B的路线去捉,结果在距离C点1.2米的D处捉住了老鼠。已知老鼠的速度是猫的 ,则阶梯A C的长度是 。
四、计算题
18.填表。
根据 =20填写下表。
y 40 80 110 150
x 1.5 5 6.5
根据xy=48填写下表。
y 12 0.5 120 240
x 6 7.5 8
五、解答题
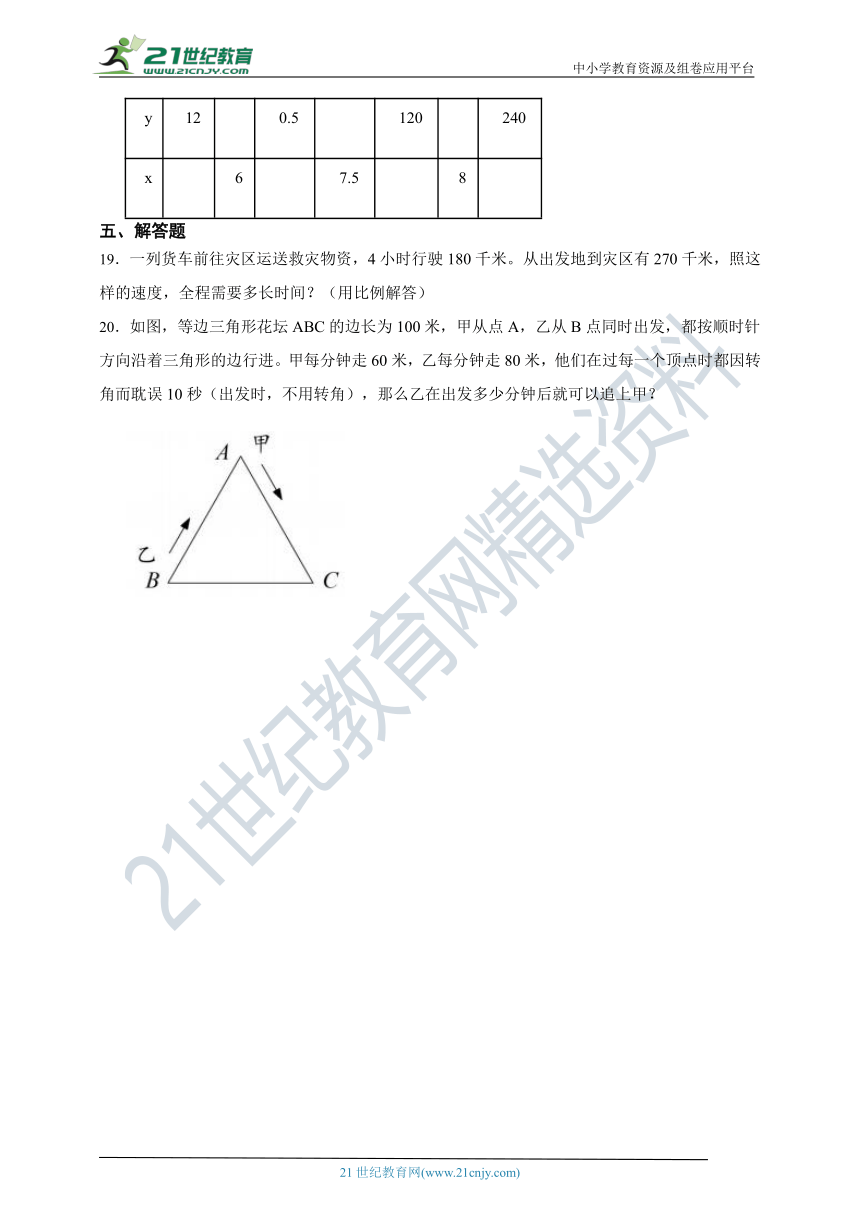
19.一列货车前往灾区运送救灾物资,4小时行驶180千米。从出发地到灾区有270千米,照这样的速度,全程需要多长时间?(用比例解答)
20.如图,等边三角形花坛ABC的边长为100米,甲从点A,乙从B点同时出发,都按顺时针方向沿着三角形的边行进。甲每分钟走60米,乙每分钟走80米,他们在过每一个顶点时都因转角而耽误10秒(出发时,不用转角),那么乙在出发多少分钟后就可以追上甲?
答案解析部分
1.【答案】C
【考点】成正比例的量及其意义
【解析】【解答】A、a与b的和一定,二者不成比例;
B、a与b的乘积一定,二者成反比例;
C、a÷b=,比值一定,二者成正比例。
故答案为:C.
【分析】根据数量关系判断a与b是乘积一定还是商(比值)一定,如果乘积一定就成反比例,如果商(比值)一定就成正比例,否则不成比例.
2.【答案】C
【考点】成正比例的量及其意义;成反比例的量及其意义
【解析】【解答】解:A:路程÷时间=速度(一定),路程和所用时间成正比例;
B:总价÷数量=单价(一定),数量和总价成正比例;
C: 长不是一定的,长方形的面积和宽不成比例;
D:圆锥的体积÷高=底面积÷3(一定),体积和高成正比例。
故答案为:C。
【分析】正比例的判断方法:相关联,能变化,商一定。
3.【答案】A
【考点】成正比例的量及其意义
【解析】【解答】解:出勤人数÷出勤率=全班人数,出勤人数和出勤率的商一定,二者成正比例。
故答案为:A。
【分析】根据出勤率的计算公式判断出出勤人数和出勤率的商一定还是乘积一定,如果商一定就成正比例,如果乘积一定就成反比例,否则不成比例。
4.【答案】C
【考点】成反比例的量及其意义
【解析】【解答】解:今年妈妈的年龄是儿子的3倍,明年就不是3倍了,比值不固定,不成比例。
故答案为:C。
【分析】正比例的判断方法:相关联,能变化,商一定;
反比例的判断方法:相关联,能变化,积一定。
5.【答案】B
【考点】正比例应用题
【解析】【解答】解:设这个月可以超额生产x吨,
23:5=(100+x):30
5(100+x)=23×30
500+5x=690
5x=690-500
x=190÷5
x=38
故答案为:B
【分析】生产的重量÷天数=每天生产的重量,每天生产的重量不变,生产的总重量与天数成正比例,先设出未知数,根据每天生产的重量不变列出比例解答即可.
6.【答案】(1)错误
【考点】成正比例的量及其意义
【解析】【解答】解:小海跳高的高度和他的身高的乘积和比值都不一定,所以小海跳高的高度和他的身高不成比例。
故答案为:错误。
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量。
7.【答案】(1)正
【考点】成反比例的量及其意义
【解析】【解答】解:乘积是1的两个数互为倒数,一个非零自然数×它的倒数=1(一定),积一定,一个非零自然数与它的倒数成反比例关系。
故答案为:正确。
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫做成反比例的量。
8.【答案】(1)错误
【考点】成正比例的量及其意义;成反比例的量及其意义
【解析】【解答】解:圆的周长和面积不成比例。
故答案为:错误。
【分析】圆的周长=2πr,圆的面积=πr ,因为圆的面积÷圆的周长=(非定值),所以,圆的周长和面积不成比例。
9.【答案】(1)错误
【考点】成正比例的量及其意义;成反比例的量及其意义
【解析】【解答】解:两种量不成正比例或者成反比例,或者不成比例。
故答案为:错误。
【分析】两种量可能成正比例、反比例、不成比例。
10.【答案】(1)正
【考点】成正比例的量及其意义
【解析】【解答】解:圆锥的高一定,圆锥的体积和底面积成正比例。原题说法正确。
故答案为:正确。
【分析】圆锥的体积÷底面积=高(一定),所以圆锥的体积和底面积成正比例。
11.【答案】(1)错误
【考点】成正比例的量及其意义
【解析】【解答】解:正方体的体积与棱长不成比例。
故答案为:错误。
【分析】棱长×棱长×棱长=正方体的体积,正方体的体积随着棱长的变化而变化,但是正方体的体积与棱长的比值(即=棱长×棱长)不固定,所以正方体的体积与棱长不成比例。
12.【答案】8;2
【考点】成正比例的量及其意义;成反比例的量及其意义
【解析】【解答】解:如果x和y成正比例,12÷4=3,24÷3=8,“?”处填8;
如果x和y成反比例,12×4=48,24÷48=2,“?”处填2。
故答案为:8;2。
【分析】如果成正比例,说明x和y的比值一定,先根据一组对应的数据求出比值,然后用24除以这个比值即可求出“?”处表示的数;如果成反比例,说明x和y的乘积一定,先根据一组对应的数据求出乘积,然后用乘积除以24即可求出“?”处表示的数。
13.【答案】成正比例
【考点】成正比例的量及其意义
【解析】【解答】解:运煤的总量÷运的次数=每次运煤的吨数(一定),运煤的总量和运的次数成正比例。
故答案为:成正比例。
【分析】正比例的判断方法:相关联,能变化,商一定。
14.【答案】比例;正
【考点】比例的认识及组成比例的判断;成正比例的量及其意义
【解析】【解答】 用数学的眼光来看成语“立竿见影”,是应用了本学期所学的比例知识。即同一时间,同一地点,竿高和影长成正比例。
故答案为:比例;正。
【分析】比例:表示两个比相等的式子叫比例;
即同一时间,同一地点,竿高和影长的比值相等,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
15.【答案】正;660
【考点】成正比例的量及其意义
【解析】【解答】解:这是一个正比例图像,这辆汽车行驶的时间与路程成正比例。6.6小时行驶100×6.6=660(km)。
故答案为:正;660。
【分析】路程÷时间=速度,速度不变,路程与时间成正比例,正比例图像是一条经过原点的射线。用每小时行驶的路程乘时间即可求出6.6小时行驶的路程。
16.【答案】10;行数;每行人数;乘积;反
【考点】成反比例的量及其意义
【解析】【解答】解:60=12×5=10×6,所以每行站10人,能站6行。行数随着每行人数的变化而变化,且它们的乘积一定,所以每行人数和行数成反比例。
故答案为:10;行数;每行人数;乘积;反。
【分析】用总人数除以行数求出每行站的人数。一个量变化,另一个量也随着变化,这两个相关联的量的乘积一定,这两个量就是成反比例的量。
17.【答案】27.6
【考点】正比例应用题
【解析】【解答】解:把楼梯的各条线段进行平移,可得AB+BC=楼梯A→C的总长;
设A→C的路程为x米,则猫行走的路程为x+1.2米,老鼠行走的路程为x 1.2米,
因为猫和老鼠行走的时间相同,且老鼠的速度是猫的 ,
根据时间一定时,路程与速度成正比的性质可得:
(x-1.2):(x+1.2)=
12(x 1.2)=11(x+1.2)
12x 14.4=11x+13.2
12x 11=14.4+13.2
x=27.6
所以阶梯A→C的长度是27.6米。
故答案为:27.6.
【分析】把楼梯的各条线段进行平移,可得AB+BC=楼梯A→C的总长,设楼梯的总长为x米,根据题中的信息可得猫行走的路程为x+1.2米,老鼠行走的路程为x 1.2米,由于猫和老鼠用的时间相同,根据时间一定,路程和速度成成比例可得出(x-1.2):(x+1.2)= ,根据比例的基本性质求解即可得出答案。
18.【答案】解:根据 =20填写下表
y 40 30 80 100 110 130 150
x 2 1.5 4 5 5.5 6.5 7.5
根据xy =48填写下表
y 12 8 0.5 6.4 120 6 240
x 4 6 96 7.5 0.4 8 0.2
【考点】正比例应用题;反比例应用题
【解析】【分析】第一个表格中:已知,所以得:,;
第二个表格中:已知,所以得:,。
19.【答案】解:设全程需要x小时。
270:x=180:4
180x=270×4
x=1080÷180
x=6
答:全程需要6小时。
【考点】正比例应用题
【解析】【分析】照这样的速度的意思就是速度不变,那么路程与时间成正比例关系,设出未知数,然后根据路程与时间的比不变列出比例解答即可。
20.【答案】解:甲的速度:60米/分=1米/秒,1×10=10(米),
追击路程:100+10=110(米),
不考虑转角情况下的追及时间:110÷(80-60) =5.5(分)=330秒,
乙走过路程是:80×5.5=440(米),440÷100=4......40,所以乙经过4个转弯,耽误10×4=40秒
因此乙出发330+40=370秒之后追上甲
370秒=6 分
因此乙出发后追上甲的总时间:6 。
答:乙在出发后6 分钟就可以追上甲。
【考点】追及问题
【解析】【分析】 等边三角形花坛 ABC 的边长为 100 米, 则乙在甲后面100米处,因此多转了一个弯,这10秒的时间甲又前进了10米,所以可计算出乙比甲多走的路程,根据追及问题计算方法,求出不考虑转角情况下的追及时间,再加上转角耽误的时间,进而求出乙追上甲所用的时间。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
2022人教版小学数学六年级下册
第4单元 4.2正比例和反比例 同步练习
一、单选题
1.表示a、b成正比例关系的是( )
A.a+b= B.ab= C.a= b
2.下面所给例子中( )不成比例
A.速度一定时,路程和所用时间 B.单价一定时,数量和总价
C.长方形的面积和宽 D.圆锥底面积一定时,体积和高
3.全班人数一定,出勤人数和出勤率( )比例。
A.成正 B.成反 C.不成
4.今年妈妈的年龄是儿子的3倍,儿子年龄和妈妈的年龄( )
A.成正比例 B.成反比例 C.不成比例 D.无法判断
5.用比例解.
某厂原计划4月份生产化肥100吨,实际前5天就生产了23吨.照这样计算,这个月可以超额生产( )
A.28吨 B.38吨 C.83吨 D.50吨
二、判断题
6.小海跳高的高度和他的身高成正比例。( )
7.一个非零自然数与它的倒数成反比例关系。( )
8.圆的周长和面积成正比例。( )
9.两种量不成正比例就成反比例。( )
10.圆锥的高一定,圆锥的体积和底面积成正比例。( )
11.正方体的体积与棱长成正比例。( )
三、填空题
12.下表中,如果x和y成正比例,?"处填 ;如果x和y成反比例,“?“处填 。
x 4
y 12 24
13.一辆货车每次运煤的吨数一定,运煤的总量和运的次数 (成正比例、不成比例)
14.用数学的眼光来看成语“立竿见影”,是应用了本学期所学的 知识。即同一时间,同一地点,竿高和影长成 比例。
15.如图表示一辆汽车在公路上行驶的时间与路程的关系,这辆汽车行驶的时间与路程成 比例。照这样计算,该汽车6.6时行驶 km。
16.六(1)班有60人,每行站12人,能站5行;每行站 人,能站6行. 随着 的变化而变化,且它们的 一定,所以每行人数和行数成 比例.
17.如图为一阶梯的纵截面,一只老鼠沿长方形的两边A B C的路线逃跑,一只猫同时沿梯形(折线)A C B的路线去捉,结果在距离C点1.2米的D处捉住了老鼠。已知老鼠的速度是猫的 ,则阶梯A C的长度是 。
四、计算题
18.填表。
根据 =20填写下表。
y 40 80 110 150
x 1.5 5 6.5
根据xy=48填写下表。
y 12 0.5 120 240
x 6 7.5 8
五、解答题
19.一列货车前往灾区运送救灾物资,4小时行驶180千米。从出发地到灾区有270千米,照这样的速度,全程需要多长时间?(用比例解答)
20.如图,等边三角形花坛ABC的边长为100米,甲从点A,乙从B点同时出发,都按顺时针方向沿着三角形的边行进。甲每分钟走60米,乙每分钟走80米,他们在过每一个顶点时都因转角而耽误10秒(出发时,不用转角),那么乙在出发多少分钟后就可以追上甲?
答案解析部分
1.【答案】C
【考点】成正比例的量及其意义
【解析】【解答】A、a与b的和一定,二者不成比例;
B、a与b的乘积一定,二者成反比例;
C、a÷b=,比值一定,二者成正比例。
故答案为:C.
【分析】根据数量关系判断a与b是乘积一定还是商(比值)一定,如果乘积一定就成反比例,如果商(比值)一定就成正比例,否则不成比例.
2.【答案】C
【考点】成正比例的量及其意义;成反比例的量及其意义
【解析】【解答】解:A:路程÷时间=速度(一定),路程和所用时间成正比例;
B:总价÷数量=单价(一定),数量和总价成正比例;
C: 长不是一定的,长方形的面积和宽不成比例;
D:圆锥的体积÷高=底面积÷3(一定),体积和高成正比例。
故答案为:C。
【分析】正比例的判断方法:相关联,能变化,商一定。
3.【答案】A
【考点】成正比例的量及其意义
【解析】【解答】解:出勤人数÷出勤率=全班人数,出勤人数和出勤率的商一定,二者成正比例。
故答案为:A。
【分析】根据出勤率的计算公式判断出出勤人数和出勤率的商一定还是乘积一定,如果商一定就成正比例,如果乘积一定就成反比例,否则不成比例。
4.【答案】C
【考点】成反比例的量及其意义
【解析】【解答】解:今年妈妈的年龄是儿子的3倍,明年就不是3倍了,比值不固定,不成比例。
故答案为:C。
【分析】正比例的判断方法:相关联,能变化,商一定;
反比例的判断方法:相关联,能变化,积一定。
5.【答案】B
【考点】正比例应用题
【解析】【解答】解:设这个月可以超额生产x吨,
23:5=(100+x):30
5(100+x)=23×30
500+5x=690
5x=690-500
x=190÷5
x=38
故答案为:B
【分析】生产的重量÷天数=每天生产的重量,每天生产的重量不变,生产的总重量与天数成正比例,先设出未知数,根据每天生产的重量不变列出比例解答即可.
6.【答案】(1)错误
【考点】成正比例的量及其意义
【解析】【解答】解:小海跳高的高度和他的身高的乘积和比值都不一定,所以小海跳高的高度和他的身高不成比例。
故答案为:错误。
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量。
7.【答案】(1)正
【考点】成反比例的量及其意义
【解析】【解答】解:乘积是1的两个数互为倒数,一个非零自然数×它的倒数=1(一定),积一定,一个非零自然数与它的倒数成反比例关系。
故答案为:正确。
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫做成反比例的量。
8.【答案】(1)错误
【考点】成正比例的量及其意义;成反比例的量及其意义
【解析】【解答】解:圆的周长和面积不成比例。
故答案为:错误。
【分析】圆的周长=2πr,圆的面积=πr ,因为圆的面积÷圆的周长=(非定值),所以,圆的周长和面积不成比例。
9.【答案】(1)错误
【考点】成正比例的量及其意义;成反比例的量及其意义
【解析】【解答】解:两种量不成正比例或者成反比例,或者不成比例。
故答案为:错误。
【分析】两种量可能成正比例、反比例、不成比例。
10.【答案】(1)正
【考点】成正比例的量及其意义
【解析】【解答】解:圆锥的高一定,圆锥的体积和底面积成正比例。原题说法正确。
故答案为:正确。
【分析】圆锥的体积÷底面积=高(一定),所以圆锥的体积和底面积成正比例。
11.【答案】(1)错误
【考点】成正比例的量及其意义
【解析】【解答】解:正方体的体积与棱长不成比例。
故答案为:错误。
【分析】棱长×棱长×棱长=正方体的体积,正方体的体积随着棱长的变化而变化,但是正方体的体积与棱长的比值(即=棱长×棱长)不固定,所以正方体的体积与棱长不成比例。
12.【答案】8;2
【考点】成正比例的量及其意义;成反比例的量及其意义
【解析】【解答】解:如果x和y成正比例,12÷4=3,24÷3=8,“?”处填8;
如果x和y成反比例,12×4=48,24÷48=2,“?”处填2。
故答案为:8;2。
【分析】如果成正比例,说明x和y的比值一定,先根据一组对应的数据求出比值,然后用24除以这个比值即可求出“?”处表示的数;如果成反比例,说明x和y的乘积一定,先根据一组对应的数据求出乘积,然后用乘积除以24即可求出“?”处表示的数。
13.【答案】成正比例
【考点】成正比例的量及其意义
【解析】【解答】解:运煤的总量÷运的次数=每次运煤的吨数(一定),运煤的总量和运的次数成正比例。
故答案为:成正比例。
【分析】正比例的判断方法:相关联,能变化,商一定。
14.【答案】比例;正
【考点】比例的认识及组成比例的判断;成正比例的量及其意义
【解析】【解答】 用数学的眼光来看成语“立竿见影”,是应用了本学期所学的比例知识。即同一时间,同一地点,竿高和影长成正比例。
故答案为:比例;正。
【分析】比例:表示两个比相等的式子叫比例;
即同一时间,同一地点,竿高和影长的比值相等,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
15.【答案】正;660
【考点】成正比例的量及其意义
【解析】【解答】解:这是一个正比例图像,这辆汽车行驶的时间与路程成正比例。6.6小时行驶100×6.6=660(km)。
故答案为:正;660。
【分析】路程÷时间=速度,速度不变,路程与时间成正比例,正比例图像是一条经过原点的射线。用每小时行驶的路程乘时间即可求出6.6小时行驶的路程。
16.【答案】10;行数;每行人数;乘积;反
【考点】成反比例的量及其意义
【解析】【解答】解:60=12×5=10×6,所以每行站10人,能站6行。行数随着每行人数的变化而变化,且它们的乘积一定,所以每行人数和行数成反比例。
故答案为:10;行数;每行人数;乘积;反。
【分析】用总人数除以行数求出每行站的人数。一个量变化,另一个量也随着变化,这两个相关联的量的乘积一定,这两个量就是成反比例的量。
17.【答案】27.6
【考点】正比例应用题
【解析】【解答】解:把楼梯的各条线段进行平移,可得AB+BC=楼梯A→C的总长;
设A→C的路程为x米,则猫行走的路程为x+1.2米,老鼠行走的路程为x 1.2米,
因为猫和老鼠行走的时间相同,且老鼠的速度是猫的 ,
根据时间一定时,路程与速度成正比的性质可得:
(x-1.2):(x+1.2)=
12(x 1.2)=11(x+1.2)
12x 14.4=11x+13.2
12x 11=14.4+13.2
x=27.6
所以阶梯A→C的长度是27.6米。
故答案为:27.6.
【分析】把楼梯的各条线段进行平移,可得AB+BC=楼梯A→C的总长,设楼梯的总长为x米,根据题中的信息可得猫行走的路程为x+1.2米,老鼠行走的路程为x 1.2米,由于猫和老鼠用的时间相同,根据时间一定,路程和速度成成比例可得出(x-1.2):(x+1.2)= ,根据比例的基本性质求解即可得出答案。
18.【答案】解:根据 =20填写下表
y 40 30 80 100 110 130 150
x 2 1.5 4 5 5.5 6.5 7.5
根据xy =48填写下表
y 12 8 0.5 6.4 120 6 240
x 4 6 96 7.5 0.4 8 0.2
【考点】正比例应用题;反比例应用题
【解析】【分析】第一个表格中:已知,所以得:,;
第二个表格中:已知,所以得:,。
19.【答案】解:设全程需要x小时。
270:x=180:4
180x=270×4
x=1080÷180
x=6
答:全程需要6小时。
【考点】正比例应用题
【解析】【分析】照这样的速度的意思就是速度不变,那么路程与时间成正比例关系,设出未知数,然后根据路程与时间的比不变列出比例解答即可。
20.【答案】解:甲的速度:60米/分=1米/秒,1×10=10(米),
追击路程:100+10=110(米),
不考虑转角情况下的追及时间:110÷(80-60) =5.5(分)=330秒,
乙走过路程是:80×5.5=440(米),440÷100=4......40,所以乙经过4个转弯,耽误10×4=40秒
因此乙出发330+40=370秒之后追上甲
370秒=6 分
因此乙出发后追上甲的总时间:6 。
答:乙在出发后6 分钟就可以追上甲。
【考点】追及问题
【解析】【分析】 等边三角形花坛 ABC 的边长为 100 米, 则乙在甲后面100米处,因此多转了一个弯,这10秒的时间甲又前进了10米,所以可计算出乙比甲多走的路程,根据追及问题计算方法,求出不考虑转角情况下的追及时间,再加上转角耽误的时间,进而求出乙追上甲所用的时间。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
