2.1.1倾斜角与斜率 学案(Word版无答案)
文档属性
| 名称 | 2.1.1倾斜角与斜率 学案(Word版无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 103.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-17 00:00:00 | ||
图片预览

文档简介
倾斜角与斜率
【学习目标】
知识目标:
1.在平面直角坐标系中,结合具体图形,探索确定直线位置的几何要素。
2.理解直线的倾斜角和斜率的概念,理解它们之间的关系。
3.掌握过两点的直线斜率的计算公式。
能力目标:
1.能用概念和公式解决有关问题。
2.培养学生观察、探索能力,运用数学语言表达能力,数学交流与评价能力.
【学习过程】
知识链接
1.三角函数的定义:在直角三角形中,内α为锐角, , ,
。
2.数轴上任意两点间的距离公式:
一、倾斜角的概念:
看一看:预习。
填一填:
1.当 时,我们取 作为基准, 与直线l 之间所成
的角α叫做直线l的倾斜角。当 时,我们规定它的倾斜角为。
2.直线倾斜角的范围是 。
想一想:对于平面直角坐标系内的一条直线,它的位置由哪些条件确定呢?(结合课件演示)
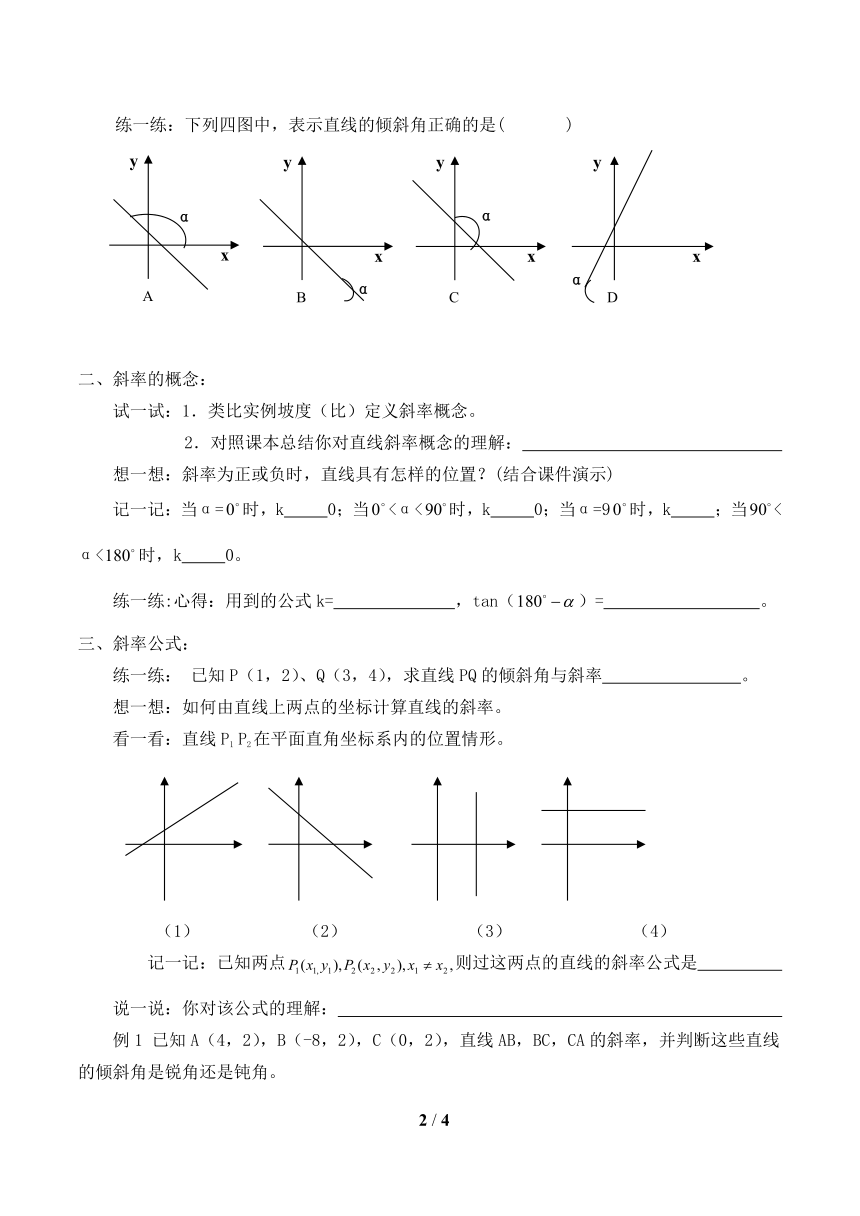
练一练:下列四图中,表示直线的倾斜角正确的是( )
二、斜率的概念:
试一试:1.类比实例坡度(比)定义斜率概念。
2.对照课本总结你对直线斜率概念的理解:
想一想:斜率为正或负时,直线具有怎样的位置?(结合课件演示)
记一记:当α=时,k 0;当<α<时,k 0;当α=9时,k ;当<α<时,k 0。
练一练:心得:用到的公式k= ,tan()= 。
三、斜率公式:
练一练: 已知P(1,2)、Q(3,4),求直线PQ的倾斜角与斜率 。
想一想:如何由直线上两点的坐标计算直线的斜率。
看一看:直线P1 P2在平面直角坐标系内的位置情形。
(1) (2) (3) (4)
记一记:已知两点则过这两点的直线的斜率公式是
说一说:你对该公式的理解:
例1 已知A(4,2),B(-8,2),C(0,2),直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角。
例2 在平面直角坐标系中,画出经过原点且斜率分别为1,-1,2及-3的直线l1,l2,l3及l4。
拓展例题:若三点A(4,5)、B(-2a,-3)、C(1,a)共线,则a =__________
练一练:求证:A(1,-1)、B(-2,-7)、C(0,-3)三点共线。
【达标检测】
1.若过点P(-2,m)和Q(m,4)的直线的斜率为1,则m的值为( )
A.1 B.4 C.1或3 D.1或4
2.直线l经过原点和(-1,1),则它的倾斜角是( )
A. B. C.或 D.-
3.若A(3,-2),B(-9,4),C(x,0)三点共线,则x的值为( )
A .1 B.-1 C.0 D.7
【学习小结】
1.直线的倾斜角定义及其范围:
2.直线的斜率定义:
3.斜率k与倾斜角之间的关系:
4.斜率公式:
【自我检测】
1.如图,若图中直线的倾斜角和斜率分别是和,则( )
(A) (B)
(C) (D)
2.已知直线斜率的绝对值等于1,则直线的倾斜角为 。
3.已知A(x,-2),B(3,0), 且 ,求x的值。
4.已知三点A(-2,3),B(3,-4m),C(,m)在同一条直线上,求实数m的值。
x
y
A
x
y
D
x
y
C
x
y
B
α
α
α
α
x
y
A
2 / 4
【学习目标】
知识目标:
1.在平面直角坐标系中,结合具体图形,探索确定直线位置的几何要素。
2.理解直线的倾斜角和斜率的概念,理解它们之间的关系。
3.掌握过两点的直线斜率的计算公式。
能力目标:
1.能用概念和公式解决有关问题。
2.培养学生观察、探索能力,运用数学语言表达能力,数学交流与评价能力.
【学习过程】
知识链接
1.三角函数的定义:在直角三角形中,内α为锐角, , ,
。
2.数轴上任意两点间的距离公式:
一、倾斜角的概念:
看一看:预习。
填一填:
1.当 时,我们取 作为基准, 与直线l 之间所成
的角α叫做直线l的倾斜角。当 时,我们规定它的倾斜角为。
2.直线倾斜角的范围是 。
想一想:对于平面直角坐标系内的一条直线,它的位置由哪些条件确定呢?(结合课件演示)
练一练:下列四图中,表示直线的倾斜角正确的是( )
二、斜率的概念:
试一试:1.类比实例坡度(比)定义斜率概念。
2.对照课本总结你对直线斜率概念的理解:
想一想:斜率为正或负时,直线具有怎样的位置?(结合课件演示)
记一记:当α=时,k 0;当<α<时,k 0;当α=9时,k ;当<α<时,k 0。
练一练:心得:用到的公式k= ,tan()= 。
三、斜率公式:
练一练: 已知P(1,2)、Q(3,4),求直线PQ的倾斜角与斜率 。
想一想:如何由直线上两点的坐标计算直线的斜率。
看一看:直线P1 P2在平面直角坐标系内的位置情形。
(1) (2) (3) (4)
记一记:已知两点则过这两点的直线的斜率公式是
说一说:你对该公式的理解:
例1 已知A(4,2),B(-8,2),C(0,2),直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角。
例2 在平面直角坐标系中,画出经过原点且斜率分别为1,-1,2及-3的直线l1,l2,l3及l4。
拓展例题:若三点A(4,5)、B(-2a,-3)、C(1,a)共线,则a =__________
练一练:求证:A(1,-1)、B(-2,-7)、C(0,-3)三点共线。
【达标检测】
1.若过点P(-2,m)和Q(m,4)的直线的斜率为1,则m的值为( )
A.1 B.4 C.1或3 D.1或4
2.直线l经过原点和(-1,1),则它的倾斜角是( )
A. B. C.或 D.-
3.若A(3,-2),B(-9,4),C(x,0)三点共线,则x的值为( )
A .1 B.-1 C.0 D.7
【学习小结】
1.直线的倾斜角定义及其范围:
2.直线的斜率定义:
3.斜率k与倾斜角之间的关系:
4.斜率公式:
【自我检测】
1.如图,若图中直线的倾斜角和斜率分别是和,则( )
(A) (B)
(C) (D)
2.已知直线斜率的绝对值等于1,则直线的倾斜角为 。
3.已知A(x,-2),B(3,0), 且 ,求x的值。
4.已知三点A(-2,3),B(3,-4m),C(,m)在同一条直线上,求实数m的值。
x
y
A
x
y
D
x
y
C
x
y
B
α
α
α
α
x
y
A
2 / 4
