1.4 充分条件与必要条件 课件(共17张PPT)
文档属性
| 名称 | 1.4 充分条件与必要条件 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1004.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-16 23:04:38 | ||
图片预览






文档简介
(共17张PPT)
第1章 集合与常用逻辑用语
1.4 充分条件与必要条件
人教A版2019高中数学必修第一册
B
A
什么是充分条件?什么是必要条件?
观察下面的例子,你能发现集合之间有什么关系吗?
(1)A={1,2},B={1,2,3}
(2)集合A={| 是奇数},集合B={| 是整数}
可以发现,在(1)(2)中,如果元素属于集合A,那么一定也属于B。
一般地,“若p,则q”为真命题,是指由p可以推导出q,记作:pq,
并且说p是q的充分条件;q是p的必要条件。反之,如果由p不能推导出q,那
么就说p不是q的充分条件,q不是p的必要条件,记作:pq
p
q
我是你的充分条件
我是你的必要条件
p q
什么是充分条件?什么是必要条件?
【对充分与必要条件的理解】
①p是q的充分条件说明pq,而q是p的必要
条件也说明了pq,所以:
“p是q的充分条件”和 “q是p的必要条
件”表述的是同一个逻辑关系。
而“p是q的充分条件”只能说明pq,
与q能否推导出p没有任何关系。
②注意右侧等价的表述方式:
【1】 pq
【2】 p是q的充分条件
【3】 q的充分条件是p
【4】 q是p的必要条件
【5】 p的必要条件是q
1.用符号“”与“”填空。
① ______ . ②都是偶数 ______ 是偶数.
2.下列说法是否正确?
①“”是“”的充分条件;
② “”是“”的必要条件
【解】① 或,所以填“”;
②偶数+偶数=偶数,所以填“”
【解】① 当时,左边不能推导出右边,则这种说法错误;
② ,所以,右边可以推导出左边,正确。
本资料分享自高中数学同步资源千人教师QQ群483122854 本群专注同步资源收集 期待你的加入与分享
什么是充要条件?
【逆命题】将命题“若p,则q”中的条件和结论互换,就得到一个新的命题:
“若q,则p”,这个就是原命题的逆命题。
【充要条件】
一般地,如果p可以推导出q,并且q也可以推导出p,即pq,且有
q p,则相当于pq或者q p,称作q是p的充分必要条件,q也是p的
充分必要条件,简称充要条件
【注意】充要条件是相互的,同时存在的, pq即p和q互为充要条件.
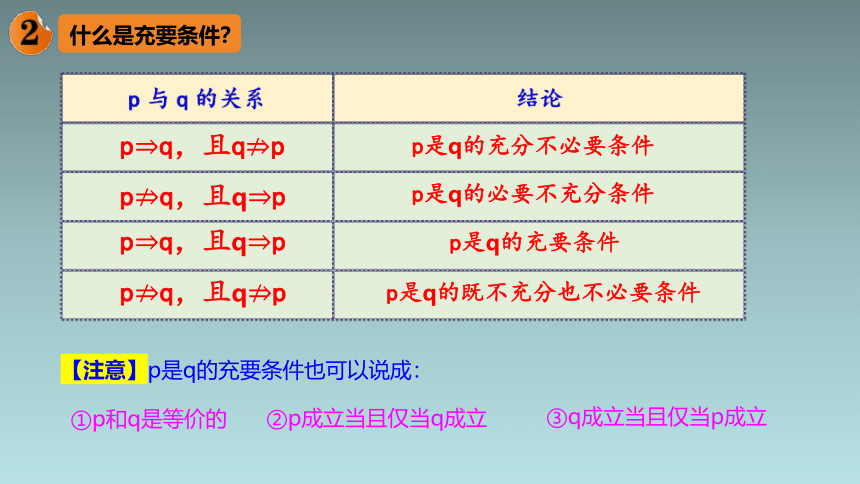
什么是充要条件?
【注意】p是q的充要条件也可以说成:
pq,且qp
pq,且qp
pq,且qp
pq,且qp
p是q的充分不必要条件
p是q的必要不充分条件
p是q的充要条件
p是q的既不充分也不必要条件
①p和q是等价的
②p成立当且仅当q成立
③q成立当且仅当p成立
1.指出下列各组中p是q的什么条件。
①p:两个三角形相似,q:两个三角形全等;
【解】相似不一定全等,pq;全等一定相似,qp,
所以p是q的必要要不充分条件
② p:一个四边形是矩形,q:四边形的对角线相等;
【解】矩形的对角线相等, pq ;对角线相等的四边形不一定是矩形,
也可能是等腰梯形等, qp ,所以p是q的充分不必要条件
2.设集合A={1,,-2} ,集合B={2,4},则“”是“”的
( )条件.
A.充分不必要 B.必要不充分 C.充要 D.既不充分也不必要
【解】若,则A={1,4,-2},,满足充分条件要求;
若或,不满足必要条件要求;
所以“”是“”的充分不必要条件,选A
A
怎么判断充要条件?有哪些方法?
【2】等价法
【1】定义法:
(1)分清命题的条件和结论
(2)找推式,判断的真假
(3)根据条件和推式得出结论
将命题转化成为另一个与之等价的且便于判断真假的命题
【3】赋值法
对于选择题,可以取一些特殊值或者特殊情况,用来说明
结论或者推导不成立,但不可用于证明题。
怎么判断充要条件?有哪些方法?
【3】集合法:
列出集合A={|p()}和集合B={|q()} ,利用集合的
包含关系来判断,如图:
A
B
A
B
B
B
A
A
A(B)
A B
p是q的充分不必要条件
B A
p是q的必要不充分条件
A=B
p是q的充要条件
AB且BA
p是q的既不充分也不必要条件
1.指出下列各组中p是q的什么条件。
①p:;q:
【解】化简,p:∈{2,3};q:,则q代表的集合Q是p代表的集合P
的真子集,即Q P,所以p是q的必要不充分条件
②p:四边形的对角线相等;q:四边形是矩形
【解】对角线相等的四边形不一定是矩形,pq;
矩形的对角线相等,qp,所以p是q的必要不充分条件
充分条件与必要条件的传递性
①若pq,qs则有ps,即p是s的充分条件;
(1)充分条件与必要条件都有传递性,具体如下:
②若sq,qp则有sp,即p是s的必要条件;
③若pq,qs,则有ps,即p是s的充要条件;
(2)给定命题“若p,则q”,对于p是q的什么条件的证明:
①证明充分性,则需证明pq;
②证明必要性,则需证明qp;
充分条件与必要条件的传递性
【问题】已知p,q都是r的充分条件,s是r的必要条件,q是s的必要条件,那么:
①s是q的什么条件? ②r是q的什么条件? ③p是q的什么条件?
【解】利用图示,表示出p,q,s,r之间的关系如下:
①因为qr,rs,所以qs;又有sq,所以s是q的充要条件
②因为rs,sq,所以rq;又有qr,所以r是q的充要条件
③因为pr,rs,sq,所以pq;又有qp,所以p是q的充分不必要条件
1.下列各组题中, 哪些p是q的充要条件?为什么?
①p:三角形为等腰三角形,q:三角形存在两角相等;
【解】因为p和q代表的都是等腰三角形,所以p=q,
即pq,p是q的充要条件;
②p:圆O内两条弦相等,q:圆O内两条弦所对的圆周角相等;
【解】圆O内两条弦相等,则它们所对的圆周角相等或互补,因此pq,
所以p不是q的充要条件;
本节考试常考什么?
【充分条件,必要条件,充要条件的判断】
【题1·定义法】判断下列各题中p是q的什么条件?
①p:,q:;
【解】因为 ,但 ,
所以p是q的充分不必要条件;
②p:两个三角形相似,q:两个三角形全等;
【解】因为相似不一定全等,但全等一定相似,即pq,qp,
所以p是q的必要不充分条件;
③p:,q:;
【解】因为由p推导到q和由q推导到p都是等式的基本性质,所以pq且qp,
所以p是q的充要条件.
本节考试常考什么?
【充分条件,必要条件,充要条件的判断】
【题2·集合法】判断下列各图中A是B的什么条件?
①
【解】因为B A,所以A是B的充分不必要条件
②
③
B
A
A(B)
A
B
【解】因为A=B,所以A是B的充要条件
【解】因为AB且BA,所以A是B的
既不充分也不必要条件
本节考试常考什么?
【充分条件,必要条件,充要条件的判断】
【题3·传递法】已知p是r的充分不必要条件,q是r的充分条件,s是r的必要条件,q是s
的必要条件,则p是q的什么条件?
【解】由题意有pr,rp,qr,rs,sq,所以prsq,
而, qrp,即p是q的充分不必要条件.
【注意】本题也可以用图形法,列出p,q,r,s的关系图:
在图中路径prsq可以走通,但 qrp走不通,同样可以得出结论.
第1章 集合与常用逻辑用语
1.4 充分条件与必要条件
人教A版2019高中数学必修第一册
B
A
什么是充分条件?什么是必要条件?
观察下面的例子,你能发现集合之间有什么关系吗?
(1)A={1,2},B={1,2,3}
(2)集合A={| 是奇数},集合B={| 是整数}
可以发现,在(1)(2)中,如果元素属于集合A,那么一定也属于B。
一般地,“若p,则q”为真命题,是指由p可以推导出q,记作:pq,
并且说p是q的充分条件;q是p的必要条件。反之,如果由p不能推导出q,那
么就说p不是q的充分条件,q不是p的必要条件,记作:pq
p
q
我是你的充分条件
我是你的必要条件
p q
什么是充分条件?什么是必要条件?
【对充分与必要条件的理解】
①p是q的充分条件说明pq,而q是p的必要
条件也说明了pq,所以:
“p是q的充分条件”和 “q是p的必要条
件”表述的是同一个逻辑关系。
而“p是q的充分条件”只能说明pq,
与q能否推导出p没有任何关系。
②注意右侧等价的表述方式:
【1】 pq
【2】 p是q的充分条件
【3】 q的充分条件是p
【4】 q是p的必要条件
【5】 p的必要条件是q
1.用符号“”与“”填空。
① ______ . ②都是偶数 ______ 是偶数.
2.下列说法是否正确?
①“”是“”的充分条件;
② “”是“”的必要条件
【解】① 或,所以填“”;
②偶数+偶数=偶数,所以填“”
【解】① 当时,左边不能推导出右边,则这种说法错误;
② ,所以,右边可以推导出左边,正确。
本资料分享自高中数学同步资源千人教师QQ群483122854 本群专注同步资源收集 期待你的加入与分享
什么是充要条件?
【逆命题】将命题“若p,则q”中的条件和结论互换,就得到一个新的命题:
“若q,则p”,这个就是原命题的逆命题。
【充要条件】
一般地,如果p可以推导出q,并且q也可以推导出p,即pq,且有
q p,则相当于pq或者q p,称作q是p的充分必要条件,q也是p的
充分必要条件,简称充要条件
【注意】充要条件是相互的,同时存在的, pq即p和q互为充要条件.
什么是充要条件?
【注意】p是q的充要条件也可以说成:
pq,且qp
pq,且qp
pq,且qp
pq,且qp
p是q的充分不必要条件
p是q的必要不充分条件
p是q的充要条件
p是q的既不充分也不必要条件
①p和q是等价的
②p成立当且仅当q成立
③q成立当且仅当p成立
1.指出下列各组中p是q的什么条件。
①p:两个三角形相似,q:两个三角形全等;
【解】相似不一定全等,pq;全等一定相似,qp,
所以p是q的必要要不充分条件
② p:一个四边形是矩形,q:四边形的对角线相等;
【解】矩形的对角线相等, pq ;对角线相等的四边形不一定是矩形,
也可能是等腰梯形等, qp ,所以p是q的充分不必要条件
2.设集合A={1,,-2} ,集合B={2,4},则“”是“”的
( )条件.
A.充分不必要 B.必要不充分 C.充要 D.既不充分也不必要
【解】若,则A={1,4,-2},,满足充分条件要求;
若或,不满足必要条件要求;
所以“”是“”的充分不必要条件,选A
A
怎么判断充要条件?有哪些方法?
【2】等价法
【1】定义法:
(1)分清命题的条件和结论
(2)找推式,判断的真假
(3)根据条件和推式得出结论
将命题转化成为另一个与之等价的且便于判断真假的命题
【3】赋值法
对于选择题,可以取一些特殊值或者特殊情况,用来说明
结论或者推导不成立,但不可用于证明题。
怎么判断充要条件?有哪些方法?
【3】集合法:
列出集合A={|p()}和集合B={|q()} ,利用集合的
包含关系来判断,如图:
A
B
A
B
B
B
A
A
A(B)
A B
p是q的充分不必要条件
B A
p是q的必要不充分条件
A=B
p是q的充要条件
AB且BA
p是q的既不充分也不必要条件
1.指出下列各组中p是q的什么条件。
①p:;q:
【解】化简,p:∈{2,3};q:,则q代表的集合Q是p代表的集合P
的真子集,即Q P,所以p是q的必要不充分条件
②p:四边形的对角线相等;q:四边形是矩形
【解】对角线相等的四边形不一定是矩形,pq;
矩形的对角线相等,qp,所以p是q的必要不充分条件
充分条件与必要条件的传递性
①若pq,qs则有ps,即p是s的充分条件;
(1)充分条件与必要条件都有传递性,具体如下:
②若sq,qp则有sp,即p是s的必要条件;
③若pq,qs,则有ps,即p是s的充要条件;
(2)给定命题“若p,则q”,对于p是q的什么条件的证明:
①证明充分性,则需证明pq;
②证明必要性,则需证明qp;
充分条件与必要条件的传递性
【问题】已知p,q都是r的充分条件,s是r的必要条件,q是s的必要条件,那么:
①s是q的什么条件? ②r是q的什么条件? ③p是q的什么条件?
【解】利用图示,表示出p,q,s,r之间的关系如下:
①因为qr,rs,所以qs;又有sq,所以s是q的充要条件
②因为rs,sq,所以rq;又有qr,所以r是q的充要条件
③因为pr,rs,sq,所以pq;又有qp,所以p是q的充分不必要条件
1.下列各组题中, 哪些p是q的充要条件?为什么?
①p:三角形为等腰三角形,q:三角形存在两角相等;
【解】因为p和q代表的都是等腰三角形,所以p=q,
即pq,p是q的充要条件;
②p:圆O内两条弦相等,q:圆O内两条弦所对的圆周角相等;
【解】圆O内两条弦相等,则它们所对的圆周角相等或互补,因此pq,
所以p不是q的充要条件;
本节考试常考什么?
【充分条件,必要条件,充要条件的判断】
【题1·定义法】判断下列各题中p是q的什么条件?
①p:,q:;
【解】因为 ,但 ,
所以p是q的充分不必要条件;
②p:两个三角形相似,q:两个三角形全等;
【解】因为相似不一定全等,但全等一定相似,即pq,qp,
所以p是q的必要不充分条件;
③p:,q:;
【解】因为由p推导到q和由q推导到p都是等式的基本性质,所以pq且qp,
所以p是q的充要条件.
本节考试常考什么?
【充分条件,必要条件,充要条件的判断】
【题2·集合法】判断下列各图中A是B的什么条件?
①
【解】因为B A,所以A是B的充分不必要条件
②
③
B
A
A(B)
A
B
【解】因为A=B,所以A是B的充要条件
【解】因为AB且BA,所以A是B的
既不充分也不必要条件
本节考试常考什么?
【充分条件,必要条件,充要条件的判断】
【题3·传递法】已知p是r的充分不必要条件,q是r的充分条件,s是r的必要条件,q是s
的必要条件,则p是q的什么条件?
【解】由题意有pr,rp,qr,rs,sq,所以prsq,
而, qrp,即p是q的充分不必要条件.
【注意】本题也可以用图形法,列出p,q,r,s的关系图:
在图中路径prsq可以走通,但 qrp走不通,同样可以得出结论.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
