华东师大版数学八年级下册第17章 函数及其图像同步练习试卷(含解析)
文档属性
| 名称 | 华东师大版数学八年级下册第17章 函数及其图像同步练习试卷(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 305.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-16 22:02:17 | ||
图片预览


文档简介
华东师大版数学八年级下册第17章 函数及其图像同步练习
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、已知点和都在反比例函数的图象上,如果,那么与的大小关系是( )
A. B. C. D.无法判断
2、下列函数中,y是x的一次函数的是( )
A.y= B.y=﹣3x+1 C.y=2 D.y=x2+1
3、如果点P(﹣5,b)在第二象限,那么b的取值范围是( )
A.b≥0 B.b≤0 C.b<0 D.b>0
4、已知点与点都在反比例函数的图象上,那么m与n的关系是( )
A. B. C. D.不能确定
5、下列各点中,在第二象限的点是( )
A. B. C. D.
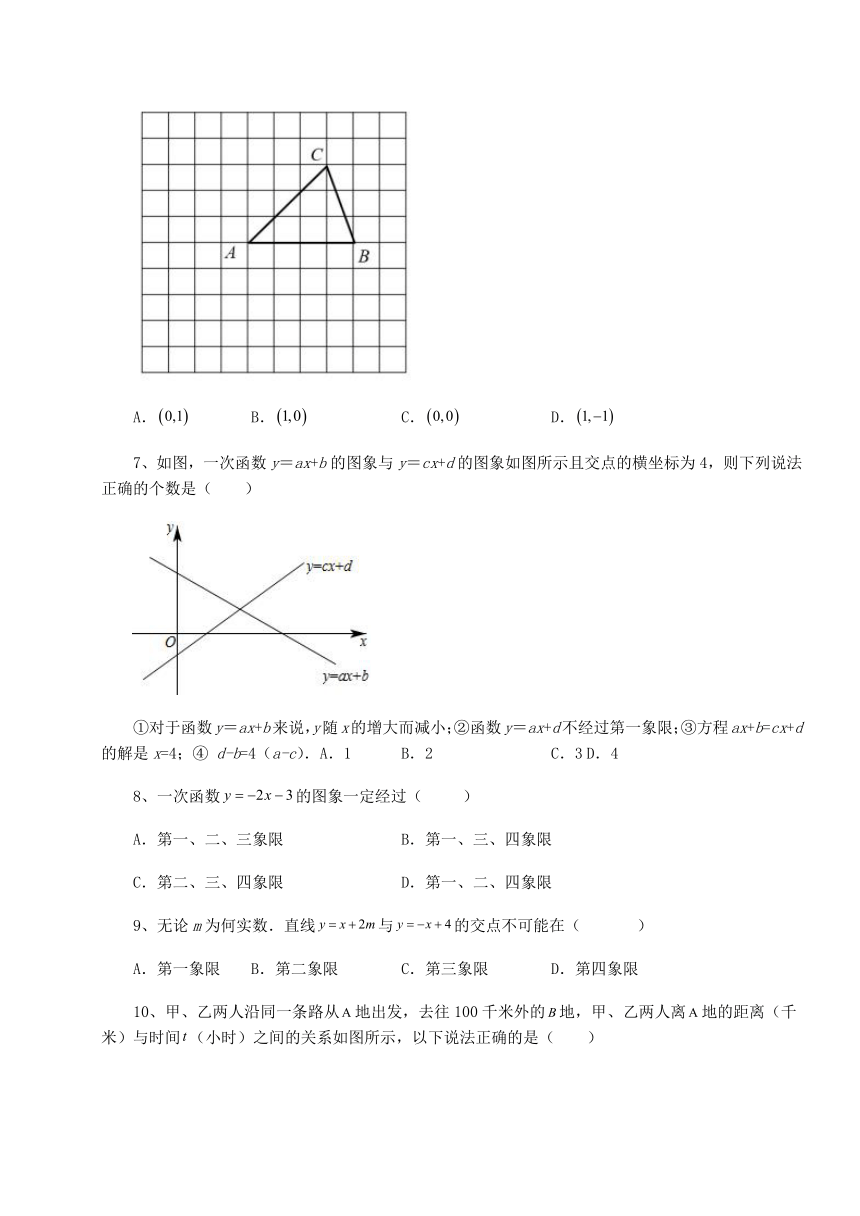
6、如图,网格中的每个小正方形边长均为1,的顶点均落在格点上,若点A的坐标为,则到三个顶点距离相等的点的坐标为( )
A. B. C. D.
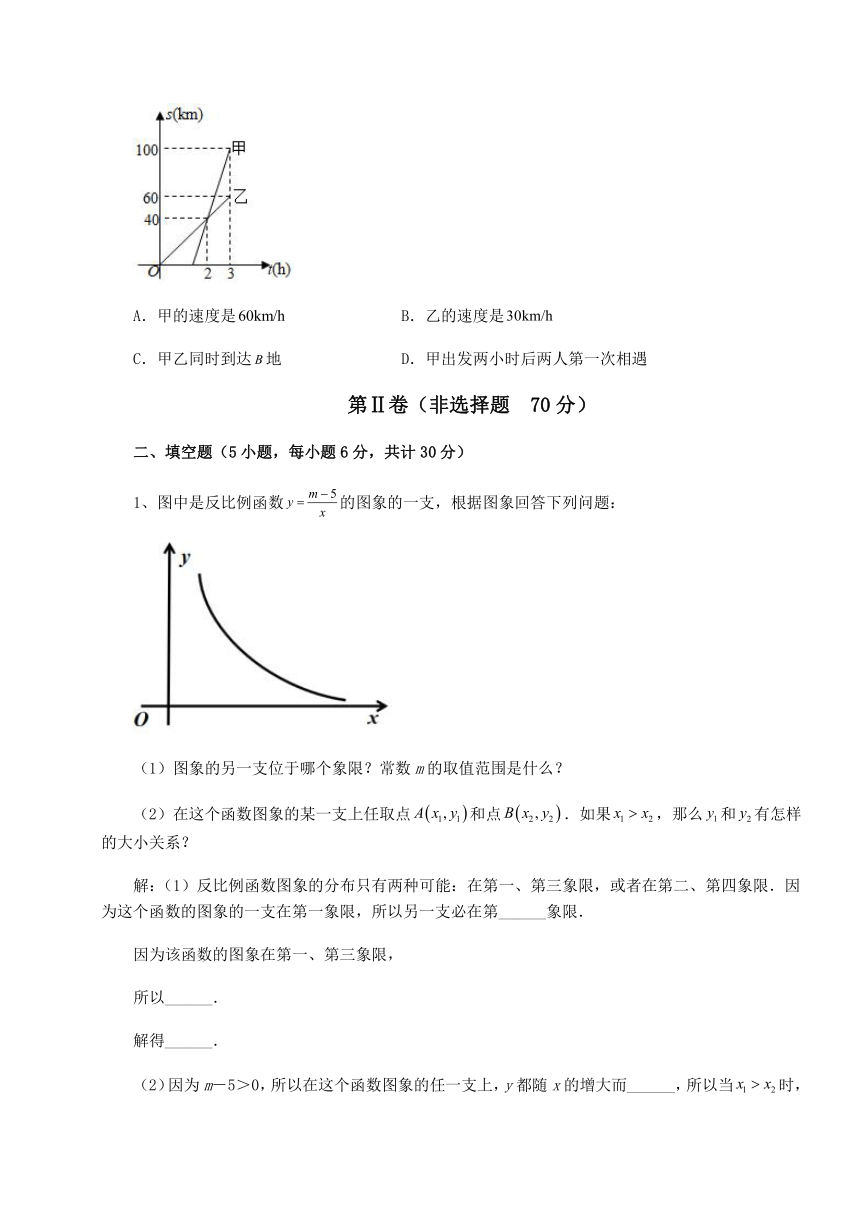
7、如图,一次函数y=ax+b的图象与y=cx+d的图象如图所示且交点的横坐标为4,则下列说法正确的个数是( )
①对于函数y=ax+b来说,y随x的增大而减小;②函数y=ax+d不经过第一象限;③方程ax+b=cx+d的解是x=4;④ d-b=4(a-c).A.1 B.2 C.3 D.4
8、一次函数的图象一定经过( )
A.第一、二、三象限 B.第一、三、四象限
C.第二、三、四象限 D.第一、二、四象限
9、无论m为何实数.直线与的交点不可能在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
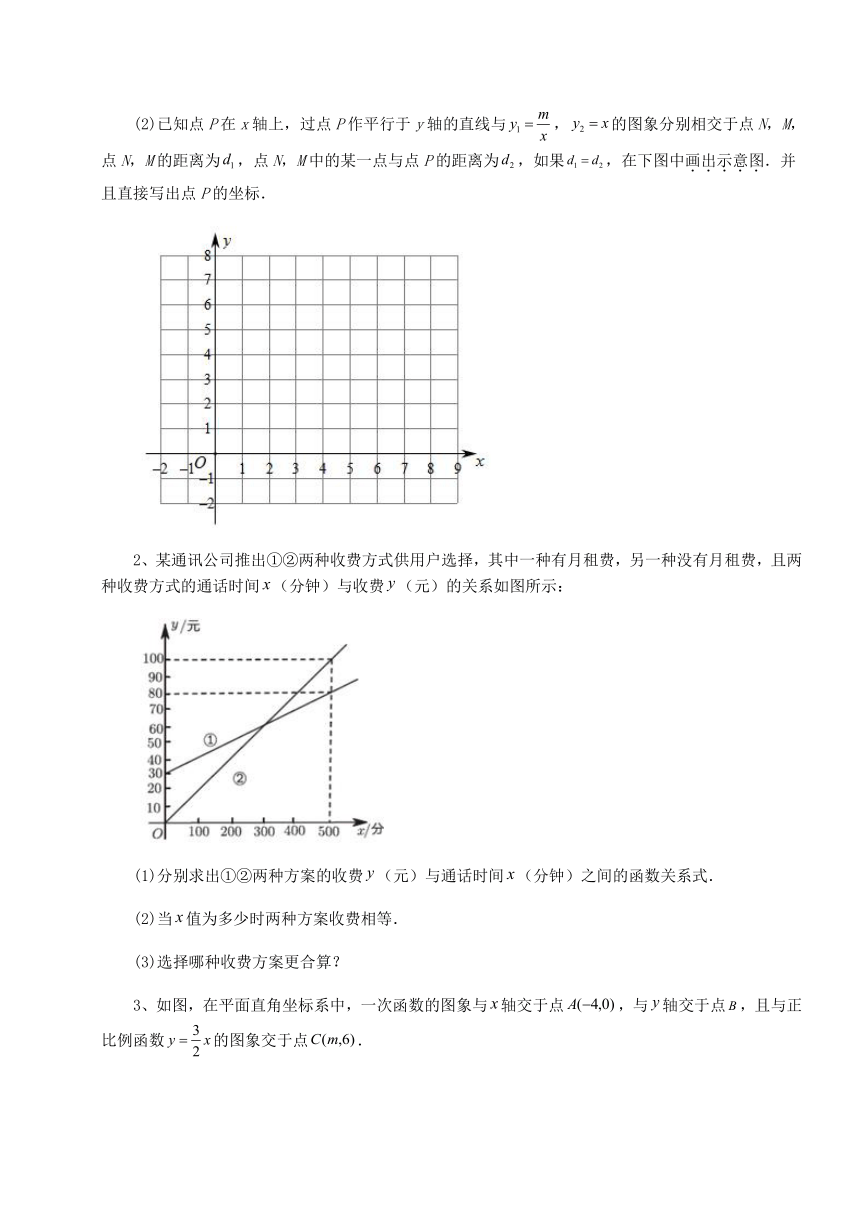
10、甲、乙两人沿同一条路从地出发,去往100千米外的地,甲、乙两人离地的距离(千米)与时间(小时)之间的关系如图所示,以下说法正确的是( )
A.甲的速度是 B.乙的速度是
C.甲乙同时到达地 D.甲出发两小时后两人第一次相遇
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题6分,共计30分)
1、图中是反比例函数的图象的一支,根据图象回答下列问题:
(1)图象的另一支位于哪个象限?常数m的取值范围是什么?
(2)在这个函数图象的某一支上任取点和点.如果,那么和有怎样的大小关系?
解:(1)反比例函数图象的分布只有两种可能:在第一、第三象限,或者在第二、第四象限.因为这个函数的图象的一支在第一象限,所以另一支必在第______象限.
因为该函数的图象在第一、第三象限,
所以______.
解得______.
(2)因为m-5>0,所以在这个函数图象的任一支上,y都随x的增大而______,所以当时,______.
2、已知f(x)=,那么f()=___.
3、在平面直角坐标系xOy中,过点A(5,3)作y轴的平行线,与x轴交于点B,直线y=kx+b(k,b为常数,k≠0)经过点A且与x轴交于点C(9,0).我们称横、纵坐标都是整数的点为整点.
(1)记线段AB,BC,CA围成的区域(不含边界)为W.请你结合函数图象,则区域W内的整点个数为______;
(2)将直线y=kx+b向下平移n个单位(n≥0),若平移后的直线与线段AB,BC围成的区域(不含边界)存在整点,请结合图象写出n的取值范围______.
4、用函数观点解决实际问题:
(1)搞清题目中的基本数量关系,将实际问题抽象成数学问题,看看各变量间应满足什么样的关系式(包括已学过的基本公式),这一步很重要;
(2)分清______和______,并注意自变量的______.
5、求kx+b>0(或<0)(k≠0)的解集
从函数值看:y=kx+b的值大于(或小于)0时,_____的取值范围
从函数图象看:直线y=kx+b在_____上方(或下方)的x取值范围
三、解答题(4小题,每小题10分,共计40分)
1、在平面直角坐标系xOy中的第一象限内,点在双曲线上.
(1)求m的值;
(2)已知点P在x轴上,过点P作平行于y轴的直线与,的图象分别相交于点N,M,点N,M的距离为,点N,M中的某一点与点P的距离为,如果,在下图中画出示意图.并且直接写出点P的坐标.
2、某通讯公司推出①②两种收费方式供用户选择,其中一种有月租费,另一种没有月租费,且两种收费方式的通话时间(分钟)与收费(元)的关系如图所示:
(1)分别求出①②两种方案的收费(元)与通话时间(分钟)之间的函数关系式.
(2)当值为多少时两种方案收费相等.
(3)选择哪种收费方案更合算?
3、如图,在平面直角坐标系中,一次函数的图象与轴交于点,与轴交于点,且与正比例函数的图象交于点.
(1)求的值与一次函数解析式;
(2)在轴上是否存在点,使得是以为腰的等腰三角形?若存在,请求出符合条件的所有点的坐标;若不存在,请说明理由.
4、下列式子,哪些y是x的正比例函数?如果是,请你指出正比例系数k的值.
(1)y=-0.1x
(2)y =
(3)y=2x2
(4)y2=4x
(5)y=-4x+3
(6)y=2(x-x2 )+2x2
-参考答案-
一、单选题
1、D
【解析】
【分析】
分两种情况讨论:先画出反比例函数的图象,再在图象上描出点和,从而可得答案.
【详解】
解:如图,当时,则
同理:当时,
如图,当时,
则
故的大小无法判断,
故选D
【点睛】
本题考查的是反比例函数的图象与性质,利用“数形结合的方法比较函数值的大小”是解本题的关键.
2、B
【解析】
【分析】
利用一般地,形如y=kx+b(k≠0,k、b是常数)的函数,叫做一次函数,进而判断得出答案.
【详解】
解:∵y=不符合一次函数的形式,故不是一次函数,
∴选项A不符合题意;
∵形如y=kx+b(k,b为常数).
∴y=﹣3x+1中,y是x的一次函数.
故选项B符合题意;
∵y=2是常数函数,
∴选项C不符合题意;
∵y=x2+1不符合一次函数的形式,故不是一次函数,
∴选项D不符合题意;
综上,y是x的一次函数的是选项B.
故选:B.
【点睛】
本题主要考查了一次函数的定义,正确把握一次函数的定义是解题关键.
3、D
【解析】
【分析】
点在第二象限的条件是:横坐标是负数,纵坐标是正数,据此可得到b的取值范围.
【详解】
解:∵点P(﹣5,b)在第二象限,
∴b>0,
故选D.
【点睛】
本题考查了平面直角坐标系中点的坐标特征,正确掌握各象限内点的坐标特点是解题关键.第一象限内点的坐标特征为(+,+),第二象限内点的坐标特征为(-,+),第三象限内点的坐标特征为(-,-),第四象限内点的坐标特征为(+,-),x轴上的点纵坐标为0,y轴上的点横坐标为0.
4、A
【解析】
【分析】
判断出反比例函数的图象在第一、三象限,从而可得出,,由此即可得出答案.
【详解】
解:,
反比例函数的图象在第一、三象限,
,
在第三象限的图象上,在第一象限的图象上,
,
,
故选:A.
【点睛】
本题考查了反比例函数的图象,熟练掌握反比例函数的图象的特点是解题关键.
5、D
【解析】
【分析】
根据第二象限内的点的横坐标为负,纵坐标为正判断即可.
【详解】
解:∵第二象限内的点的横坐标为负,纵坐标为正,
∴在第二象限,
故选:D.
【点睛】
本题考查了象限内点的坐标的特征,解题关键是熟记第二象限内点的横坐标为负,纵坐标为正.
6、C
【解析】
【分析】
到△ABC三个顶点距离相等的点是AB与AC的垂直平分线的交点,画出交点,进而得出其坐标即可.
【详解】
解:平面直角坐标系如图所示,AB与AC的垂直平分线的交点为点O,
∴到△ABC三个顶点距离相等的点的坐标为(0,0),
故选:C.
【点睛】
本题主要考查了线段垂直平分线的性质,线段垂直平分线上任意一点,到线段两端点的距离相等.
7、C
【解析】
【分析】
仔细观察图象:①观察函数图象可以直接得到答案;
②观察函数图象可以直接得到答案;
③根据函数y=ax+b的图象与y=cx+d的图象如图所示且交点的横坐标为4可以得到答案;
④根据函数y=ax+b的图象与y=cx+d的图象如图所示且交点的横坐标为4可以得到答案.
【详解】
解:由图象可得,对于函数y=ax+b来说,y随x的增大而减小故①正确;
函数y=ax+d图象经过第一,三,四象限,即不经过第二象限,故②不正确,
一次函数y=ax+b的图象与y=cx+d的图象如图所示且交点的横坐标为4,所以方程ax+b=cx+d的解是x=4;故③正确;
∵一次函数y=ax+b的图象与y=cx+d的图象如图所示且交点的横坐标为4,
∴4a+b=4c+d
∴d-b=4(a-c),故④正确.
综上所述,正确的结论有3个.
故选:C.
【点睛】
本题主要考查了一次函数的图象与性质,利用数形结合是解题的关键.
8、C
【解析】
【分析】
k<0,函数一定经过第二,四象限,b<0,直线与y轴交于负半轴,所以函数图象过第三象限.
【详解】
解:∵k=-2<0,b=-3<0,
∴函数的图象经过第二、三、四象限,
故选:C.
【点睛】
本题考查了一次函数的性质,k>0,函数一定经过第一,三象限,k<0,函数一定经过第二,四象限,再根据直线与y轴的交点即可得出函数所过的象限,这是解题的关键.
9、C
【解析】
【分析】
根据一次函数的图象与系数的关系即可得出结论.
【详解】
解:∵一次函数y=-x+4中,k=-1<0,b=4>0,
∴函数图象经过一二四象限,
∴无论m为何实数,直线y=x+2m与y=-x+4的交点不可能在第三象限.
故选:C.
【点睛】
本题考查的是两条直线相交或平行问题,熟知一次函数的图象与系数的关系是解答此题的关键.
10、A
【解析】
【分析】
根据函数图象中的数据,可以计算出各个选项中的说法是否正确,然后即可判断哪个选项中的说法是否正确.
【详解】
解:由图象可得,
甲的速度是,故选项符合题意;
乙的速度为:,故选项不符合题意;
甲先到达地,故选项不符合题意;
甲出发小时后两人第一次相遇,故选项不符合题意;
故选:A.
【点睛】
本题考查一次函数的应用,解题的关键是利用数形结合的思想解答.
二、填空题
1、 三 m-5>0 m>5 减小
【解析】
略
2、
【解析】
【分析】
把代入函数解析式进行计算即可.
【点睛】
本题考查的是已知自变量的值求解函数值,理解的含义是解本题的关键.
3、 3 ≤n<
【解析】
【分析】
(1)根据题意和图象,可以得到区域W内的整点个数;
(2)根据直线y=kx+b过点A和点C,从而可以得到直线的表达式是y=-x+,设平移后的直线解析式是y=-x+m,分别代入(6,2)、(6,1)求得m的值,结合图象即可求得.
【详解】
解:(1)由图象可得,
区域W内的整点的坐标分别为(6,1),(6,2),(7,1),
即区域W内的整点个数是3个,
故答案为:3;
(2)∵直线y=kx+b过点A(5,3),点C(9,0),
∴,
∴,
即直线y=kx+b的表达式是y=﹣x+,
设平移后的直线解析式是y=﹣x+m,
把(6,2)代入得,2=﹣+m,解得m=,则﹣=,
把(6,1)代入得,1=﹣+m,解得m=,则﹣=,
由图象可知,将直线y=kx+b向下平移n个单位(n≥0),若平移后的直线与线段AB,BC围成的区域(不含边界)存在整点,请结合图象写出n的取值范围≤n<.
故答案为:≤n<.
【点睛】
本题考查了一次函数图象与几何变换、待定系数法求一次函数解析式,解答本题的关键是明确题意,利用数形结合的思想解答.
4、 自变量 函数 取值范围
【解析】
略
5、 x x轴
【解析】
略
三、解答题
1、 (1)8
(2)点P的坐标为(2,0)或(4,0)或(-2,0)或(-4,0).
【解析】
【分析】
(1)根据待定系数法即可求得;
(2)画出函数的图象,根据图象即可求得.
(1)
解:∵点A(2,4)在双曲线(m≠0)上,
∴m=2×4=8,
∴m的值为8;
(2)
解:如图:
由图象可知,点P的坐标为(2,0)或(4,0)或(-2,0)或(-4,0).
【点睛】
本题考查了待定系数法求反比例函数的解析式,反比例函数图象上点的坐标特征,数形结合是解题的关键.
2、 (1)①:y=0.1x+30;②:y=0.2x
(2)当x值为300时两种方案收费相等
(3)当0<x<300时,选择②种方案;当x=300时,两种方案一样;当x>300时,选择①种方案.
【解析】
【分析】
(1)根据函数图象中的数据,用待定系数法可以分别求得①②两种方案的收费y(元)与通话时间x(分钟)之间的函数关系式;
(2)令(1)中的两个函数值相等,即可求出当x值为多少时两种方案收费相等;
(3)根据(2)中的结果和函数图象,可以写出当x何值时,选择哪种收费方案更合算.
(1)
解:设①种方案的收费y(元)与通话时间x(分钟)之间的函数关系式是y=kx+b,
∵点(0,30),(500,80)在此函数图象上,
∴,
解得
,
即①种方案的收费y(元)与通话时间x(分钟)之间的函数关系式是y=0.1x+30;
设②种方案的收费y(元)与通话时间x(分钟)之间的函数关系式是y=ax,
∵点(500,100)在此函数图象上,
∴100=500a,得a=0.2,
即②种方案的收费y(元)与通话时间x(分钟)之间的函数关系式是y=0.2x;
(2)
解:令0.1x+30=0.2x,
解得x=300,
答:当x值为300时两种方案收费相等;
(3)
解:由(2)中的结果和图象可得,
当0<x<300时,选择②种方案;
当x=300时,两种方案一样;
当x>300时,选择①种方案.
【点睛】
本题考查一次函数的应用,解答本题的关键是明确题意,求出相应的函数解析式,利用数形结合的思想解答.
3、 (1),
(2)存在,,,
【解析】
【分析】
(1)根据正比例函数过,可得,设一次函数解析式为(k≠0).把,代入,即可求解;
(2)先求出AB=5,然后分两种情况:或,即可求解.
(1)
解:∵正比例函数过,
,
,
∴点,
设一次函数解析式为(k≠0).
将,代入,得
,
,
∴一次函数解析式为.
(2)
(2),,
,
是以为腰的等腰三角形,
或,
①若,
设,则,
解得:或-1,
,;
②若,则,
,
综上,,,.
【点睛】
本题主要考查了一次函数的性质和图象,待定系数法求一次函数解析式,等腰三角形的性质,熟练掌握一次函数的性质和图象,并利用数形结合和分论讨论思想思想解答是解题的关键.
4、 (1)是正比例函数,正比例系数是-0.1
(2)是正比例函数,正比例系数是
(3)不是正比例函数
(4)不是正比例函数
(5)不是正比例函数
(6)是正比例函数,正比例系数是2
【解析】
略
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、已知点和都在反比例函数的图象上,如果,那么与的大小关系是( )
A. B. C. D.无法判断
2、下列函数中,y是x的一次函数的是( )
A.y= B.y=﹣3x+1 C.y=2 D.y=x2+1
3、如果点P(﹣5,b)在第二象限,那么b的取值范围是( )
A.b≥0 B.b≤0 C.b<0 D.b>0
4、已知点与点都在反比例函数的图象上,那么m与n的关系是( )
A. B. C. D.不能确定
5、下列各点中,在第二象限的点是( )
A. B. C. D.
6、如图,网格中的每个小正方形边长均为1,的顶点均落在格点上,若点A的坐标为,则到三个顶点距离相等的点的坐标为( )
A. B. C. D.
7、如图,一次函数y=ax+b的图象与y=cx+d的图象如图所示且交点的横坐标为4,则下列说法正确的个数是( )
①对于函数y=ax+b来说,y随x的增大而减小;②函数y=ax+d不经过第一象限;③方程ax+b=cx+d的解是x=4;④ d-b=4(a-c).A.1 B.2 C.3 D.4
8、一次函数的图象一定经过( )
A.第一、二、三象限 B.第一、三、四象限
C.第二、三、四象限 D.第一、二、四象限
9、无论m为何实数.直线与的交点不可能在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10、甲、乙两人沿同一条路从地出发,去往100千米外的地,甲、乙两人离地的距离(千米)与时间(小时)之间的关系如图所示,以下说法正确的是( )
A.甲的速度是 B.乙的速度是
C.甲乙同时到达地 D.甲出发两小时后两人第一次相遇
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题6分,共计30分)
1、图中是反比例函数的图象的一支,根据图象回答下列问题:
(1)图象的另一支位于哪个象限?常数m的取值范围是什么?
(2)在这个函数图象的某一支上任取点和点.如果,那么和有怎样的大小关系?
解:(1)反比例函数图象的分布只有两种可能:在第一、第三象限,或者在第二、第四象限.因为这个函数的图象的一支在第一象限,所以另一支必在第______象限.
因为该函数的图象在第一、第三象限,
所以______.
解得______.
(2)因为m-5>0,所以在这个函数图象的任一支上,y都随x的增大而______,所以当时,______.
2、已知f(x)=,那么f()=___.
3、在平面直角坐标系xOy中,过点A(5,3)作y轴的平行线,与x轴交于点B,直线y=kx+b(k,b为常数,k≠0)经过点A且与x轴交于点C(9,0).我们称横、纵坐标都是整数的点为整点.
(1)记线段AB,BC,CA围成的区域(不含边界)为W.请你结合函数图象,则区域W内的整点个数为______;
(2)将直线y=kx+b向下平移n个单位(n≥0),若平移后的直线与线段AB,BC围成的区域(不含边界)存在整点,请结合图象写出n的取值范围______.
4、用函数观点解决实际问题:
(1)搞清题目中的基本数量关系,将实际问题抽象成数学问题,看看各变量间应满足什么样的关系式(包括已学过的基本公式),这一步很重要;
(2)分清______和______,并注意自变量的______.
5、求kx+b>0(或<0)(k≠0)的解集
从函数值看:y=kx+b的值大于(或小于)0时,_____的取值范围
从函数图象看:直线y=kx+b在_____上方(或下方)的x取值范围
三、解答题(4小题,每小题10分,共计40分)
1、在平面直角坐标系xOy中的第一象限内,点在双曲线上.
(1)求m的值;
(2)已知点P在x轴上,过点P作平行于y轴的直线与,的图象分别相交于点N,M,点N,M的距离为,点N,M中的某一点与点P的距离为,如果,在下图中画出示意图.并且直接写出点P的坐标.
2、某通讯公司推出①②两种收费方式供用户选择,其中一种有月租费,另一种没有月租费,且两种收费方式的通话时间(分钟)与收费(元)的关系如图所示:
(1)分别求出①②两种方案的收费(元)与通话时间(分钟)之间的函数关系式.
(2)当值为多少时两种方案收费相等.
(3)选择哪种收费方案更合算?
3、如图,在平面直角坐标系中,一次函数的图象与轴交于点,与轴交于点,且与正比例函数的图象交于点.
(1)求的值与一次函数解析式;
(2)在轴上是否存在点,使得是以为腰的等腰三角形?若存在,请求出符合条件的所有点的坐标;若不存在,请说明理由.
4、下列式子,哪些y是x的正比例函数?如果是,请你指出正比例系数k的值.
(1)y=-0.1x
(2)y =
(3)y=2x2
(4)y2=4x
(5)y=-4x+3
(6)y=2(x-x2 )+2x2
-参考答案-
一、单选题
1、D
【解析】
【分析】
分两种情况讨论:先画出反比例函数的图象,再在图象上描出点和,从而可得答案.
【详解】
解:如图,当时,则
同理:当时,
如图,当时,
则
故的大小无法判断,
故选D
【点睛】
本题考查的是反比例函数的图象与性质,利用“数形结合的方法比较函数值的大小”是解本题的关键.
2、B
【解析】
【分析】
利用一般地,形如y=kx+b(k≠0,k、b是常数)的函数,叫做一次函数,进而判断得出答案.
【详解】
解:∵y=不符合一次函数的形式,故不是一次函数,
∴选项A不符合题意;
∵形如y=kx+b(k,b为常数).
∴y=﹣3x+1中,y是x的一次函数.
故选项B符合题意;
∵y=2是常数函数,
∴选项C不符合题意;
∵y=x2+1不符合一次函数的形式,故不是一次函数,
∴选项D不符合题意;
综上,y是x的一次函数的是选项B.
故选:B.
【点睛】
本题主要考查了一次函数的定义,正确把握一次函数的定义是解题关键.
3、D
【解析】
【分析】
点在第二象限的条件是:横坐标是负数,纵坐标是正数,据此可得到b的取值范围.
【详解】
解:∵点P(﹣5,b)在第二象限,
∴b>0,
故选D.
【点睛】
本题考查了平面直角坐标系中点的坐标特征,正确掌握各象限内点的坐标特点是解题关键.第一象限内点的坐标特征为(+,+),第二象限内点的坐标特征为(-,+),第三象限内点的坐标特征为(-,-),第四象限内点的坐标特征为(+,-),x轴上的点纵坐标为0,y轴上的点横坐标为0.
4、A
【解析】
【分析】
判断出反比例函数的图象在第一、三象限,从而可得出,,由此即可得出答案.
【详解】
解:,
反比例函数的图象在第一、三象限,
,
在第三象限的图象上,在第一象限的图象上,
,
,
故选:A.
【点睛】
本题考查了反比例函数的图象,熟练掌握反比例函数的图象的特点是解题关键.
5、D
【解析】
【分析】
根据第二象限内的点的横坐标为负,纵坐标为正判断即可.
【详解】
解:∵第二象限内的点的横坐标为负,纵坐标为正,
∴在第二象限,
故选:D.
【点睛】
本题考查了象限内点的坐标的特征,解题关键是熟记第二象限内点的横坐标为负,纵坐标为正.
6、C
【解析】
【分析】
到△ABC三个顶点距离相等的点是AB与AC的垂直平分线的交点,画出交点,进而得出其坐标即可.
【详解】
解:平面直角坐标系如图所示,AB与AC的垂直平分线的交点为点O,
∴到△ABC三个顶点距离相等的点的坐标为(0,0),
故选:C.
【点睛】
本题主要考查了线段垂直平分线的性质,线段垂直平分线上任意一点,到线段两端点的距离相等.
7、C
【解析】
【分析】
仔细观察图象:①观察函数图象可以直接得到答案;
②观察函数图象可以直接得到答案;
③根据函数y=ax+b的图象与y=cx+d的图象如图所示且交点的横坐标为4可以得到答案;
④根据函数y=ax+b的图象与y=cx+d的图象如图所示且交点的横坐标为4可以得到答案.
【详解】
解:由图象可得,对于函数y=ax+b来说,y随x的增大而减小故①正确;
函数y=ax+d图象经过第一,三,四象限,即不经过第二象限,故②不正确,
一次函数y=ax+b的图象与y=cx+d的图象如图所示且交点的横坐标为4,所以方程ax+b=cx+d的解是x=4;故③正确;
∵一次函数y=ax+b的图象与y=cx+d的图象如图所示且交点的横坐标为4,
∴4a+b=4c+d
∴d-b=4(a-c),故④正确.
综上所述,正确的结论有3个.
故选:C.
【点睛】
本题主要考查了一次函数的图象与性质,利用数形结合是解题的关键.
8、C
【解析】
【分析】
k<0,函数一定经过第二,四象限,b<0,直线与y轴交于负半轴,所以函数图象过第三象限.
【详解】
解:∵k=-2<0,b=-3<0,
∴函数的图象经过第二、三、四象限,
故选:C.
【点睛】
本题考查了一次函数的性质,k>0,函数一定经过第一,三象限,k<0,函数一定经过第二,四象限,再根据直线与y轴的交点即可得出函数所过的象限,这是解题的关键.
9、C
【解析】
【分析】
根据一次函数的图象与系数的关系即可得出结论.
【详解】
解:∵一次函数y=-x+4中,k=-1<0,b=4>0,
∴函数图象经过一二四象限,
∴无论m为何实数,直线y=x+2m与y=-x+4的交点不可能在第三象限.
故选:C.
【点睛】
本题考查的是两条直线相交或平行问题,熟知一次函数的图象与系数的关系是解答此题的关键.
10、A
【解析】
【分析】
根据函数图象中的数据,可以计算出各个选项中的说法是否正确,然后即可判断哪个选项中的说法是否正确.
【详解】
解:由图象可得,
甲的速度是,故选项符合题意;
乙的速度为:,故选项不符合题意;
甲先到达地,故选项不符合题意;
甲出发小时后两人第一次相遇,故选项不符合题意;
故选:A.
【点睛】
本题考查一次函数的应用,解题的关键是利用数形结合的思想解答.
二、填空题
1、 三 m-5>0 m>5 减小
【解析】
略
2、
【解析】
【分析】
把代入函数解析式进行计算即可.
【点睛】
本题考查的是已知自变量的值求解函数值,理解的含义是解本题的关键.
3、 3 ≤n<
【解析】
【分析】
(1)根据题意和图象,可以得到区域W内的整点个数;
(2)根据直线y=kx+b过点A和点C,从而可以得到直线的表达式是y=-x+,设平移后的直线解析式是y=-x+m,分别代入(6,2)、(6,1)求得m的值,结合图象即可求得.
【详解】
解:(1)由图象可得,
区域W内的整点的坐标分别为(6,1),(6,2),(7,1),
即区域W内的整点个数是3个,
故答案为:3;
(2)∵直线y=kx+b过点A(5,3),点C(9,0),
∴,
∴,
即直线y=kx+b的表达式是y=﹣x+,
设平移后的直线解析式是y=﹣x+m,
把(6,2)代入得,2=﹣+m,解得m=,则﹣=,
把(6,1)代入得,1=﹣+m,解得m=,则﹣=,
由图象可知,将直线y=kx+b向下平移n个单位(n≥0),若平移后的直线与线段AB,BC围成的区域(不含边界)存在整点,请结合图象写出n的取值范围≤n<.
故答案为:≤n<.
【点睛】
本题考查了一次函数图象与几何变换、待定系数法求一次函数解析式,解答本题的关键是明确题意,利用数形结合的思想解答.
4、 自变量 函数 取值范围
【解析】
略
5、 x x轴
【解析】
略
三、解答题
1、 (1)8
(2)点P的坐标为(2,0)或(4,0)或(-2,0)或(-4,0).
【解析】
【分析】
(1)根据待定系数法即可求得;
(2)画出函数的图象,根据图象即可求得.
(1)
解:∵点A(2,4)在双曲线(m≠0)上,
∴m=2×4=8,
∴m的值为8;
(2)
解:如图:
由图象可知,点P的坐标为(2,0)或(4,0)或(-2,0)或(-4,0).
【点睛】
本题考查了待定系数法求反比例函数的解析式,反比例函数图象上点的坐标特征,数形结合是解题的关键.
2、 (1)①:y=0.1x+30;②:y=0.2x
(2)当x值为300时两种方案收费相等
(3)当0<x<300时,选择②种方案;当x=300时,两种方案一样;当x>300时,选择①种方案.
【解析】
【分析】
(1)根据函数图象中的数据,用待定系数法可以分别求得①②两种方案的收费y(元)与通话时间x(分钟)之间的函数关系式;
(2)令(1)中的两个函数值相等,即可求出当x值为多少时两种方案收费相等;
(3)根据(2)中的结果和函数图象,可以写出当x何值时,选择哪种收费方案更合算.
(1)
解:设①种方案的收费y(元)与通话时间x(分钟)之间的函数关系式是y=kx+b,
∵点(0,30),(500,80)在此函数图象上,
∴,
解得
,
即①种方案的收费y(元)与通话时间x(分钟)之间的函数关系式是y=0.1x+30;
设②种方案的收费y(元)与通话时间x(分钟)之间的函数关系式是y=ax,
∵点(500,100)在此函数图象上,
∴100=500a,得a=0.2,
即②种方案的收费y(元)与通话时间x(分钟)之间的函数关系式是y=0.2x;
(2)
解:令0.1x+30=0.2x,
解得x=300,
答:当x值为300时两种方案收费相等;
(3)
解:由(2)中的结果和图象可得,
当0<x<300时,选择②种方案;
当x=300时,两种方案一样;
当x>300时,选择①种方案.
【点睛】
本题考查一次函数的应用,解答本题的关键是明确题意,求出相应的函数解析式,利用数形结合的思想解答.
3、 (1),
(2)存在,,,
【解析】
【分析】
(1)根据正比例函数过,可得,设一次函数解析式为(k≠0).把,代入,即可求解;
(2)先求出AB=5,然后分两种情况:或,即可求解.
(1)
解:∵正比例函数过,
,
,
∴点,
设一次函数解析式为(k≠0).
将,代入,得
,
,
∴一次函数解析式为.
(2)
(2),,
,
是以为腰的等腰三角形,
或,
①若,
设,则,
解得:或-1,
,;
②若,则,
,
综上,,,.
【点睛】
本题主要考查了一次函数的性质和图象,待定系数法求一次函数解析式,等腰三角形的性质,熟练掌握一次函数的性质和图象,并利用数形结合和分论讨论思想思想解答是解题的关键.
4、 (1)是正比例函数,正比例系数是-0.1
(2)是正比例函数,正比例系数是
(3)不是正比例函数
(4)不是正比例函数
(5)不是正比例函数
(6)是正比例函数,正比例系数是2
【解析】
略
