华东师大版七年级下册10.2.2 平移的特征 课件(共18张PPT)
文档属性
| 名称 | 华东师大版七年级下册10.2.2 平移的特征 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 415.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-17 22:30:35 | ||
图片预览




文档简介
(共18张PPT)
第10章 轴对称、平移与旋转
10.2.2 平移的特征
在平面内,将一个图形沿着某个方向移动一定的距离,这样的图形运动叫做图形的平移。
说明
(1)图形的平移是由移动的方向和距离决定的;
(2)图形上每个点都沿同一方向移动相同的距离;
(3)平移不改变图形的大小与形状,只改变图形的位置。
温故夯基
平移的定义:
平移的方向:是一组对应点所连的射线的方向。
平移的距离:是一组对应点所连的线段的长度。
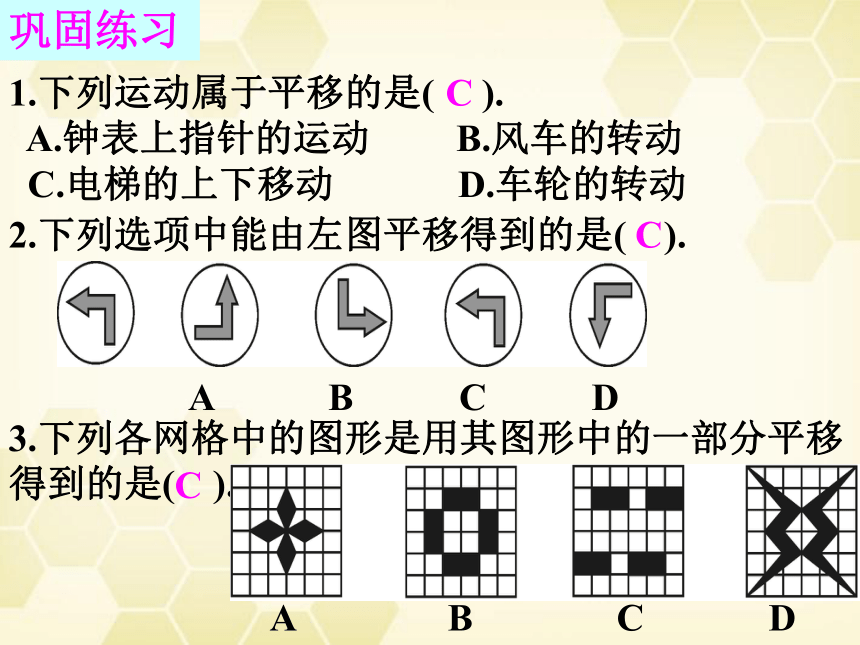
1.下列运动属于平移的是( ).
A.钟表上指针的运动 B.风车的转动
C.电梯的上下移动 D.车轮的转动
巩固练习
C
2.下列选项中能由左图平移得到的是( ).
A B C D
C
3.下列各网格中的图形是用其图形中的一部分平移
得到的是( ).
A B C D
C
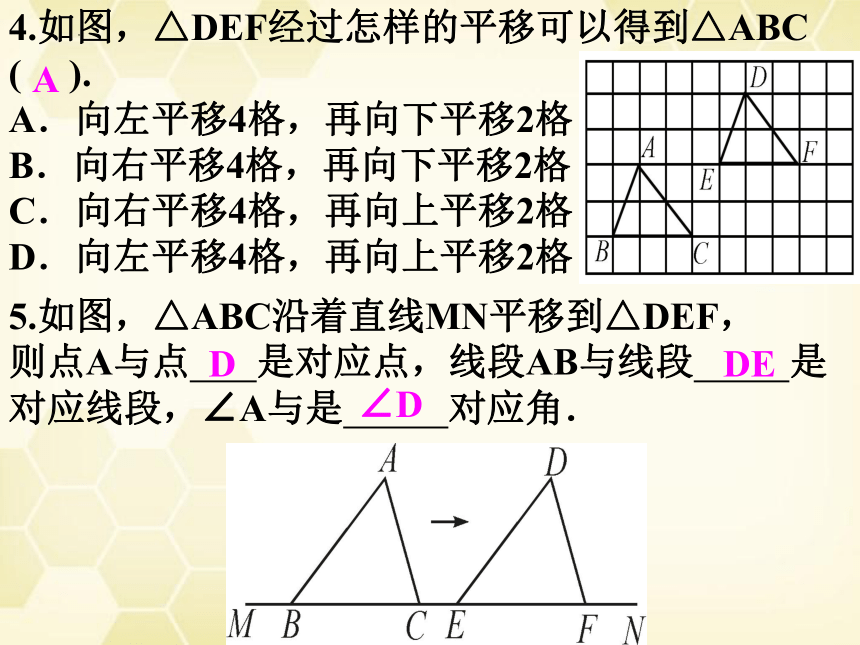
4.如图,△DEF经过怎样的平移可以得到△ABC
( ).
A.向左平移4格,再向下平移2格
B.向右平移4格,再向下平移2格
C.向右平移4格,再向上平移2格
D.向左平移4格,再向上平移2格
A
5.如图,△ABC沿着直线MN平移到△DEF,
则点A与点 是对应点,线段AB与线段 是
对应线段,∠A与是 对应角.
D
DE
∠D
动手做一做:用三角板、直尺画平行线.
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
A
B
C
0
2
1
3
4
5
6
7
8
9
10
P
Q
A
B
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
C
观察:线段AB与 A′B′ 的位置关系与数量关系,∠B与∠ B′的关系呢?
A′B′//AB
A′B′=AB
∠B′ =∠B
观察:线段AC与 A′C′ 的位置关系与数量关系,∠C与∠C′的关系呢?
A′C′//AC
A′C′ =AC
∠C′=∠C
做一做
注意:在平移过程中,对应
线段也可能在一条直线上
(如:BC与B′C′)
思考:
BC与B′C′的位置关系
与数量关系呢?
(1)平移后图形是否发生变化?
(2)平移后的图形与原来图形的对应线段、对应角有什么关系?
平移后图形的形状与大小都没有变化;
A
P
C
C′
B′
A′
B
Q
平移后的图形与原来的图形的对应线段平行(或在一条直线上,简称共线)且相等;
平移后的图形与原来的图形的对应角
相等;
平移的方向是点A到点A′的方向,
平移的距离是线段 B′B′的长度。
平移的特征
向义初中学生专用尺
0
1
2
3
4
5
6
7
8
9
10
11
Cm
学习新知
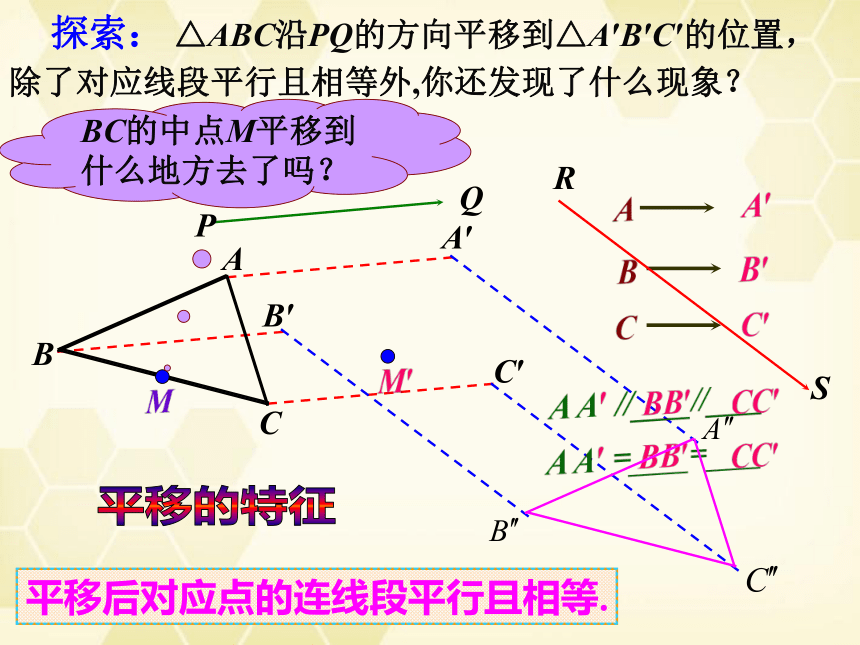
探索: △ABC沿PQ的方向平移到△A′B′C′的位置,除了对应线段平行且相等外,你还发现了什么现象?
B
A
C
P
Q
A
A′
B
B′
C
C′
A A′ //____//____
A A′ =____=____
BB′
CC′
CC′
BB′
M
M′
R
S
A′
B′
C′
BC的中点M平移到什么地方去了吗?
平移后对应点的连线段平行且相等.
平移的特征
A
P
C
C′
B′
A′
B
向义初中学生专用尺
0
1
2
3
4
5
6
7
8
9
10
11
Cm
注意:在平移过程中,对应点所连的线段也可能 在同一条直线上。如BB′与CC′。
平移的特征
Q
平移后对应点所连的线段平行
(或共线)且相等.
平移的特征
(2)平移后的图形与原来的图形的对应线段
平行(或共线)且相等;
(3)平移后的图形与原来的图形的对应角
相等;
(4)平移后对应点所连的线段平行(或共线)且相等。
(1)平移后的图形与原来的图形的形状与大小不变;
归纳总结
A
B
C
解:由于点A与点A 是一对对应点,因此,如图,连结AA ,平移的方向就是点A到点A′的方向,且平移的距离就是线段AA′的长度,约6.6厘米。
B′
C′
A′
向义初中学生专用尺
0
1
2
3
4
5
6
7
8
9
10
11
cm
例题精析
例1 如图,将△ABC平移到△A′B′C′的位置.
指出平移的方向,并量出平移的距离.(精确到mm)
1.在如图的方格纸中,画出将图中的△ABC向右平移5格后的△A B C ,然后再画出将△A B C 向上平移2格后的△A B C . △A B C 是否可以看成是△ABC 经过一次平移而得到的呢 如果是,那么平移的方向和距离分别是什么呢
A
B
C
A
B
C
A
B
C
是平移,方向为射线AA 的方向,距离约为5.39cm.
随堂练习
A
B
C
D
E
F
R
S
2.将△ABC沿RS方向平移到△DEF的位置,其平移
的距离为线段RS的长度。
例2 如图,在纸上画△ABC和两条平行的对称轴m、 n.
(1)画出△ABC关于直线m对称的△A B C ;
(2)再画出△A B C 关于直线n对称的△A B C .
C
A
B
C
m
n
A
B
A
B
C
(3)观察△ABC和△A B C ,你能发现这两个三角形
有什么关系吗
例题精析
两次翻折(对称轴要互相平行)相当于一次平移.
1.先将方格纸中的图形向左平移5格,然后再向下平移3格.
随堂练习
2.如图,在长方形ABCD中,对角线AC与BD相交于点O,画出△AOB平移后的三角形,其平移方向为射线AD的方向,平移的距离为线段AD的长。
A
B
C
D
O
(A )
(B )
(O )
3.将所给图形沿着PQ方向平移,平移的距离为
线段PQ的长度。画出平移后的新图形.
P
Q
平移的特征
(2)平移后的图形与原来的图形的对应线段
平行(或共线)且相等;
(3)平移后的图形与原来的图形的对应角
相等;
(4)平移后对应点所连的线段平行(或共线)且相等。
(1)平移后的图形与原来的图形的形状与大小不变;
课堂小结
作业与课外学习任务
1.练习作业:课本P117 习题10.2 1、3、4题
2.课外学习任务:
预习P118 10.3.1 图形的旋转
第10章 轴对称、平移与旋转
10.2.2 平移的特征
在平面内,将一个图形沿着某个方向移动一定的距离,这样的图形运动叫做图形的平移。
说明
(1)图形的平移是由移动的方向和距离决定的;
(2)图形上每个点都沿同一方向移动相同的距离;
(3)平移不改变图形的大小与形状,只改变图形的位置。
温故夯基
平移的定义:
平移的方向:是一组对应点所连的射线的方向。
平移的距离:是一组对应点所连的线段的长度。
1.下列运动属于平移的是( ).
A.钟表上指针的运动 B.风车的转动
C.电梯的上下移动 D.车轮的转动
巩固练习
C
2.下列选项中能由左图平移得到的是( ).
A B C D
C
3.下列各网格中的图形是用其图形中的一部分平移
得到的是( ).
A B C D
C
4.如图,△DEF经过怎样的平移可以得到△ABC
( ).
A.向左平移4格,再向下平移2格
B.向右平移4格,再向下平移2格
C.向右平移4格,再向上平移2格
D.向左平移4格,再向上平移2格
A
5.如图,△ABC沿着直线MN平移到△DEF,
则点A与点 是对应点,线段AB与线段 是
对应线段,∠A与是 对应角.
D
DE
∠D
动手做一做:用三角板、直尺画平行线.
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
A
B
C
0
2
1
3
4
5
6
7
8
9
10
P
Q
A
B
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
C
观察:线段AB与 A′B′ 的位置关系与数量关系,∠B与∠ B′的关系呢?
A′B′//AB
A′B′=AB
∠B′ =∠B
观察:线段AC与 A′C′ 的位置关系与数量关系,∠C与∠C′的关系呢?
A′C′//AC
A′C′ =AC
∠C′=∠C
做一做
注意:在平移过程中,对应
线段也可能在一条直线上
(如:BC与B′C′)
思考:
BC与B′C′的位置关系
与数量关系呢?
(1)平移后图形是否发生变化?
(2)平移后的图形与原来图形的对应线段、对应角有什么关系?
平移后图形的形状与大小都没有变化;
A
P
C
C′
B′
A′
B
Q
平移后的图形与原来的图形的对应线段平行(或在一条直线上,简称共线)且相等;
平移后的图形与原来的图形的对应角
相等;
平移的方向是点A到点A′的方向,
平移的距离是线段 B′B′的长度。
平移的特征
向义初中学生专用尺
0
1
2
3
4
5
6
7
8
9
10
11
Cm
学习新知
探索: △ABC沿PQ的方向平移到△A′B′C′的位置,除了对应线段平行且相等外,你还发现了什么现象?
B
A
C
P
Q
A
A′
B
B′
C
C′
A A′ //____//____
A A′ =____=____
BB′
CC′
CC′
BB′
M
M′
R
S
A′
B′
C′
BC的中点M平移到什么地方去了吗?
平移后对应点的连线段平行且相等.
平移的特征
A
P
C
C′
B′
A′
B
向义初中学生专用尺
0
1
2
3
4
5
6
7
8
9
10
11
Cm
注意:在平移过程中,对应点所连的线段也可能 在同一条直线上。如BB′与CC′。
平移的特征
Q
平移后对应点所连的线段平行
(或共线)且相等.
平移的特征
(2)平移后的图形与原来的图形的对应线段
平行(或共线)且相等;
(3)平移后的图形与原来的图形的对应角
相等;
(4)平移后对应点所连的线段平行(或共线)且相等。
(1)平移后的图形与原来的图形的形状与大小不变;
归纳总结
A
B
C
解:由于点A与点A 是一对对应点,因此,如图,连结AA ,平移的方向就是点A到点A′的方向,且平移的距离就是线段AA′的长度,约6.6厘米。
B′
C′
A′
向义初中学生专用尺
0
1
2
3
4
5
6
7
8
9
10
11
cm
例题精析
例1 如图,将△ABC平移到△A′B′C′的位置.
指出平移的方向,并量出平移的距离.(精确到mm)
1.在如图的方格纸中,画出将图中的△ABC向右平移5格后的△A B C ,然后再画出将△A B C 向上平移2格后的△A B C . △A B C 是否可以看成是△ABC 经过一次平移而得到的呢 如果是,那么平移的方向和距离分别是什么呢
A
B
C
A
B
C
A
B
C
是平移,方向为射线AA 的方向,距离约为5.39cm.
随堂练习
A
B
C
D
E
F
R
S
2.将△ABC沿RS方向平移到△DEF的位置,其平移
的距离为线段RS的长度。
例2 如图,在纸上画△ABC和两条平行的对称轴m、 n.
(1)画出△ABC关于直线m对称的△A B C ;
(2)再画出△A B C 关于直线n对称的△A B C .
C
A
B
C
m
n
A
B
A
B
C
(3)观察△ABC和△A B C ,你能发现这两个三角形
有什么关系吗
例题精析
两次翻折(对称轴要互相平行)相当于一次平移.
1.先将方格纸中的图形向左平移5格,然后再向下平移3格.
随堂练习
2.如图,在长方形ABCD中,对角线AC与BD相交于点O,画出△AOB平移后的三角形,其平移方向为射线AD的方向,平移的距离为线段AD的长。
A
B
C
D
O
(A )
(B )
(O )
3.将所给图形沿着PQ方向平移,平移的距离为
线段PQ的长度。画出平移后的新图形.
P
Q
平移的特征
(2)平移后的图形与原来的图形的对应线段
平行(或共线)且相等;
(3)平移后的图形与原来的图形的对应角
相等;
(4)平移后对应点所连的线段平行(或共线)且相等。
(1)平移后的图形与原来的图形的形状与大小不变;
课堂小结
作业与课外学习任务
1.练习作业:课本P117 习题10.2 1、3、4题
2.课外学习任务:
预习P118 10.3.1 图形的旋转
