华东师大版七年级下册10.4.2 中心对称 课件(共19张PPT)
文档属性
| 名称 | 华东师大版七年级下册10.4.2 中心对称 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 338.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-17 22:33:06 | ||
图片预览




文档简介
第10章 轴对称、平移与旋转
10.4.2 中心对称
一.中心对称图形
(1)中心对称图形首先是旋转对称图形,而且是特殊的旋转对称图形,特殊在于它必须旋转180°后才能与自身重合;
(2)旋转对称图形不一定是中心对称图形,只用当其旋转某一角度恰是180°与自身重合时,此时这个图形才是中心对称图形。
在平面内,一个图形绕某个点旋转180°后能与自身
完全重合,那么这个图形叫做中心对称图形,这个点
叫做它的对称中心。
温故夯基
二.中心对称图形的性质
中心对称图形上的每一对对应点所连成的
线段都被对称中心平分。
巩固练习
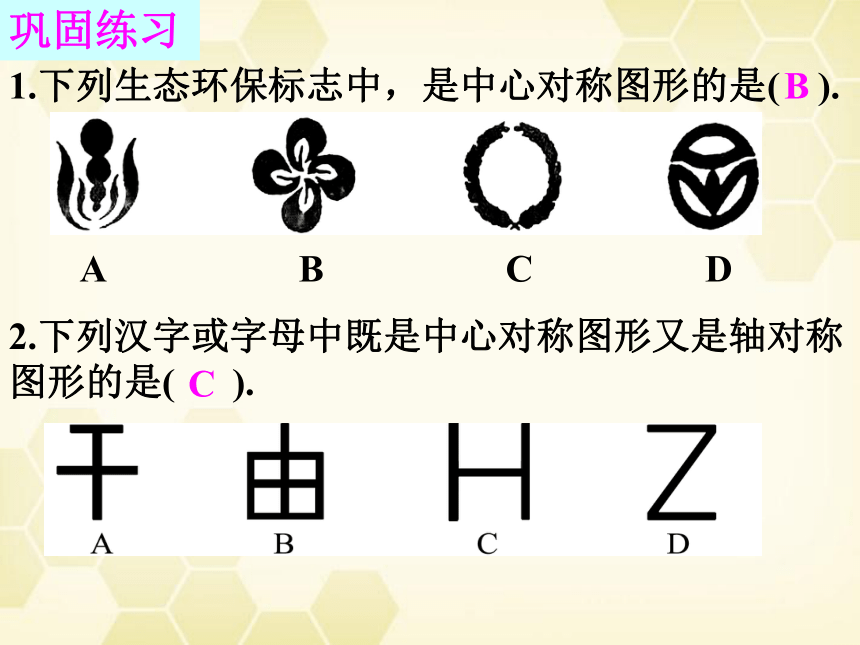
1.下列生态环保标志中,是中心对称图形的是( ).
A B C D
B
2.下列汉字或字母中既是中心对称图形又是轴对称
图形的是( ).
C
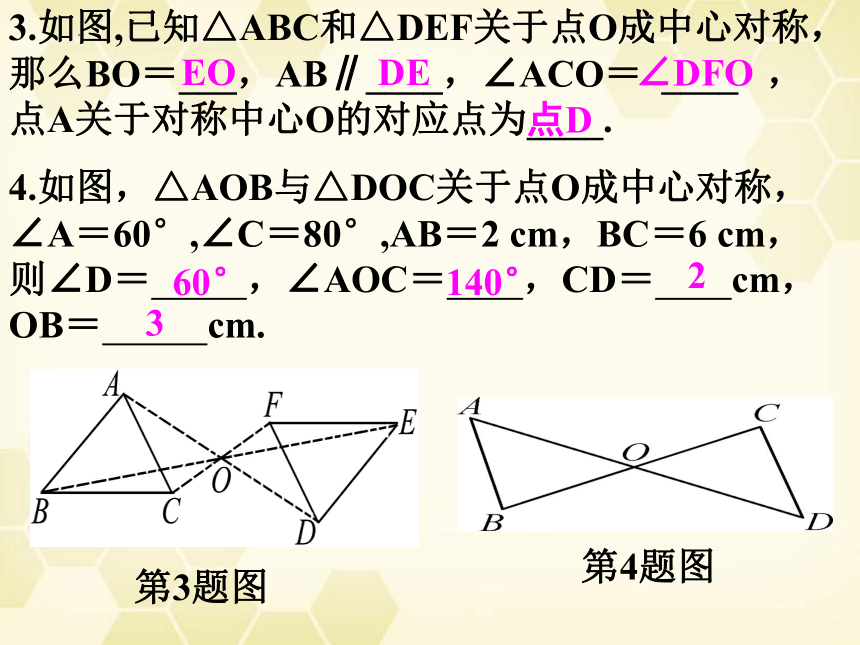
3.如图,已知△ABC和△DEF关于点O成中心对称,
那么BO=___,AB∥____,∠ACO= ____ ,
点A关于对称中心O的对应点为____.
4.如图,△AOB与△DOC关于点O成中心对称,∠A=60°,∠C=80°,AB=2 cm,BC=6 cm,
则∠D= ,∠AOC= ,CD= cm,OB= cm.
第3题图
第4题图
EO
DE
∠DFO
点D
60°
140°
2
3
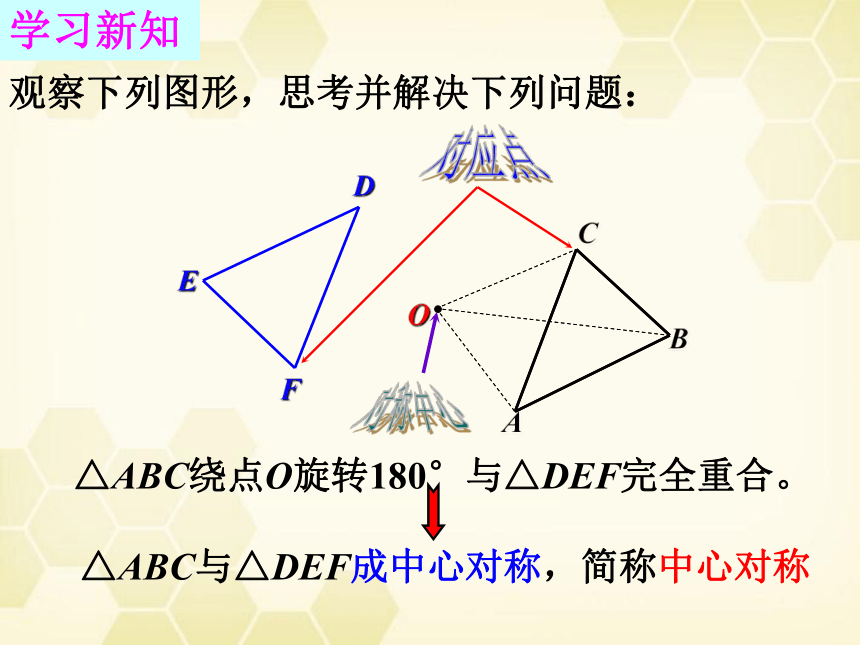
观察下列图形,思考并解决下列问题:
A
B
C
D
E
F
O
△ABC绕点O旋转180°与△DEF完全重合。
△ABC与△DEF成中心对称,简称中心对称
对应点
对称中心
学习新知
中心对称
说明:
(1)中心对称图形是指一个图形自身的对称关系,中心对称是指两个图形的对称关系;它们都要旋转180度,不同的是中心对称图形与自身重合,中心对称是与另一个图形重合。
(2)若把中心对称图形的两部分分别看作两个图形,则它们成中心对称,若把中心对称的两个图形看作一个整体,则成为中心对称图形。
在平面内,把一个图形绕着某个点旋转180°后,能和另一个图形完全重合,那么我们就说这两个图形成中心对称,这个点叫做它的对称中心,这两个图形中的对应点,叫做关于对称中心的对称点。
思考
A
B
C
O
D
E
F
△ABC和△DEF关于点O对称。
(1)A、O、D三点的位置关系怎样?线段AO、DO的大小关系呢?
A、O、D三点共线且OA=OD
(2)B、O、E三点的位置关系怎样?线段BO、EO的大小关系呢?
B、O、E三点共线且OB=OE
C、O、F三点共线且OC=OF
(3)C、O、F三点的位置关系怎样?线段CO、FO的大小关系呢?
探究发现
中心对称的性质
在成中心对称的两个图形中,连结对称点的
线段都经过对称中心,并且被对称中心平分。
反之
如果两个图形的对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形一定关于这一点成中心对称.
中心对称作图
1.点的中心对称点的作法:
A
O
A′
则点A′即为所求的点.
(1)作射线AO;
画法
(2)以点O为圆心,以OA为半径画弧,交射线AO于
点A′;
中心对称作图
2.线段的中心对称线段的作法:
A
A′
B′
B
O
则线段A′B′即为所求的线段.
D
F
E
O
A
B
C
画法
∴△DEF即为所求的三角形.
(1)连接AO并延长到D,使OD=OA,得到点A的对称点D.
(2)同样画B、C的对称点 E、F.
(3)顺次连接DE、EF、DF.
例1 如图,已知△ABC和点O,画出△DEF,使得△DEF和△ABC关于点O成中心对称。
例题精析
B
D
C
A
O
A′
B′
C′
D′
说说你的
画法吧!
B
D
C
A
O
B
D
C
A
O
例2 已知四边形ABCD和点O,画四边形
A′B′C′D′使它与已知四边形关于这一点对称.
A
B
C
A′
B′
C′
O
A
B
C
A′
B′
C′
O
例3 如图,已知△ABC与△A′B′C′中心对称,
求对称中心O.
将两个大小相等的圆部分重合,其中重叠的部分(如图(1)中的阴影部分)我们称之为一个“花瓣”,由一个“花瓣”及圆组成的图形称之为花瓣图形,图(2)是一些由“花瓣”和圆组成的图形.
随堂练习
(1)图(2)中的5个图形中是轴对称图形的有 ,是中心对称图形的有 .
(分别用图形的代号A,B,C,D,E填空)?
(2)若“花瓣”在圆中是均匀分布的,试根据上题的结果总结“花瓣”的个数与花瓣图形的对称性(轴对称或中心对称)
之间的规律 .
A,B,C,D,E
A,C,E
当花瓣是偶数个时,它既是中心对称图形也是轴对称图形;
当花瓣是奇数个时,它是轴对称图形.
(3)根据上面的结论,试判断下列花瓣图形的对称性.
①九瓣图形是 ;
②十二瓣图形是 ;
③十五瓣图形是 ;
④二十六瓣图形是 .?
(4)你还能举出类似的例子吗?
轴对称图形
轴对称图形也是中心对称图形
轴对称图形
轴对称图形也是中心对称图形
答案不唯一,合理即可.
比如正多边形,
当边数为奇数时,它只是轴对称图形;
当边数为偶数时,它既是轴对称图形,又是中心对称图形.
一.中心对称
说明:
(1)中心对称图形是指一个图形自身的对称关系,中心对称是指两个图形的对称关系;它们都要旋转180度,不同的是中心对称图形与自身重合,中心对称是与另一个图形重合。
(2)若把中心对称图形的两部分分别看作两个图形,则它们成中心对称,若把中心对称的两个图形看作一个整体,则成为中心对称图形。
在平面内,把一个图形绕着某个点旋转180°后,能和另一个图形完全重合,那么我们就说这两个图形成中心对称,这个点叫做它的对称中心,这两个图形中的对应点,叫做关于对称中心的对称点。
课堂小结
二.中心对称的性质
如果两个图形的对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形一定关于这一点成中心对称.
在成中心对称的两个图形中,连结对称点的线段都经过对称中心,并且被对称中心平分。
作业与课外学习任务
1.练习作业:书面课本P131 练习 1-2
书面课本P132 习题10.4 4,5
2.课外学习任务:
预习P133 10.5 图形的全等
教学反馈:
作业存在的主要问题:
10.4.2 中心对称
一.中心对称图形
(1)中心对称图形首先是旋转对称图形,而且是特殊的旋转对称图形,特殊在于它必须旋转180°后才能与自身重合;
(2)旋转对称图形不一定是中心对称图形,只用当其旋转某一角度恰是180°与自身重合时,此时这个图形才是中心对称图形。
在平面内,一个图形绕某个点旋转180°后能与自身
完全重合,那么这个图形叫做中心对称图形,这个点
叫做它的对称中心。
温故夯基
二.中心对称图形的性质
中心对称图形上的每一对对应点所连成的
线段都被对称中心平分。
巩固练习
1.下列生态环保标志中,是中心对称图形的是( ).
A B C D
B
2.下列汉字或字母中既是中心对称图形又是轴对称
图形的是( ).
C
3.如图,已知△ABC和△DEF关于点O成中心对称,
那么BO=___,AB∥____,∠ACO= ____ ,
点A关于对称中心O的对应点为____.
4.如图,△AOB与△DOC关于点O成中心对称,∠A=60°,∠C=80°,AB=2 cm,BC=6 cm,
则∠D= ,∠AOC= ,CD= cm,OB= cm.
第3题图
第4题图
EO
DE
∠DFO
点D
60°
140°
2
3
观察下列图形,思考并解决下列问题:
A
B
C
D
E
F
O
△ABC绕点O旋转180°与△DEF完全重合。
△ABC与△DEF成中心对称,简称中心对称
对应点
对称中心
学习新知
中心对称
说明:
(1)中心对称图形是指一个图形自身的对称关系,中心对称是指两个图形的对称关系;它们都要旋转180度,不同的是中心对称图形与自身重合,中心对称是与另一个图形重合。
(2)若把中心对称图形的两部分分别看作两个图形,则它们成中心对称,若把中心对称的两个图形看作一个整体,则成为中心对称图形。
在平面内,把一个图形绕着某个点旋转180°后,能和另一个图形完全重合,那么我们就说这两个图形成中心对称,这个点叫做它的对称中心,这两个图形中的对应点,叫做关于对称中心的对称点。
思考
A
B
C
O
D
E
F
△ABC和△DEF关于点O对称。
(1)A、O、D三点的位置关系怎样?线段AO、DO的大小关系呢?
A、O、D三点共线且OA=OD
(2)B、O、E三点的位置关系怎样?线段BO、EO的大小关系呢?
B、O、E三点共线且OB=OE
C、O、F三点共线且OC=OF
(3)C、O、F三点的位置关系怎样?线段CO、FO的大小关系呢?
探究发现
中心对称的性质
在成中心对称的两个图形中,连结对称点的
线段都经过对称中心,并且被对称中心平分。
反之
如果两个图形的对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形一定关于这一点成中心对称.
中心对称作图
1.点的中心对称点的作法:
A
O
A′
则点A′即为所求的点.
(1)作射线AO;
画法
(2)以点O为圆心,以OA为半径画弧,交射线AO于
点A′;
中心对称作图
2.线段的中心对称线段的作法:
A
A′
B′
B
O
则线段A′B′即为所求的线段.
D
F
E
O
A
B
C
画法
∴△DEF即为所求的三角形.
(1)连接AO并延长到D,使OD=OA,得到点A的对称点D.
(2)同样画B、C的对称点 E、F.
(3)顺次连接DE、EF、DF.
例1 如图,已知△ABC和点O,画出△DEF,使得△DEF和△ABC关于点O成中心对称。
例题精析
B
D
C
A
O
A′
B′
C′
D′
说说你的
画法吧!
B
D
C
A
O
B
D
C
A
O
例2 已知四边形ABCD和点O,画四边形
A′B′C′D′使它与已知四边形关于这一点对称.
A
B
C
A′
B′
C′
O
A
B
C
A′
B′
C′
O
例3 如图,已知△ABC与△A′B′C′中心对称,
求对称中心O.
将两个大小相等的圆部分重合,其中重叠的部分(如图(1)中的阴影部分)我们称之为一个“花瓣”,由一个“花瓣”及圆组成的图形称之为花瓣图形,图(2)是一些由“花瓣”和圆组成的图形.
随堂练习
(1)图(2)中的5个图形中是轴对称图形的有 ,是中心对称图形的有 .
(分别用图形的代号A,B,C,D,E填空)?
(2)若“花瓣”在圆中是均匀分布的,试根据上题的结果总结“花瓣”的个数与花瓣图形的对称性(轴对称或中心对称)
之间的规律 .
A,B,C,D,E
A,C,E
当花瓣是偶数个时,它既是中心对称图形也是轴对称图形;
当花瓣是奇数个时,它是轴对称图形.
(3)根据上面的结论,试判断下列花瓣图形的对称性.
①九瓣图形是 ;
②十二瓣图形是 ;
③十五瓣图形是 ;
④二十六瓣图形是 .?
(4)你还能举出类似的例子吗?
轴对称图形
轴对称图形也是中心对称图形
轴对称图形
轴对称图形也是中心对称图形
答案不唯一,合理即可.
比如正多边形,
当边数为奇数时,它只是轴对称图形;
当边数为偶数时,它既是轴对称图形,又是中心对称图形.
一.中心对称
说明:
(1)中心对称图形是指一个图形自身的对称关系,中心对称是指两个图形的对称关系;它们都要旋转180度,不同的是中心对称图形与自身重合,中心对称是与另一个图形重合。
(2)若把中心对称图形的两部分分别看作两个图形,则它们成中心对称,若把中心对称的两个图形看作一个整体,则成为中心对称图形。
在平面内,把一个图形绕着某个点旋转180°后,能和另一个图形完全重合,那么我们就说这两个图形成中心对称,这个点叫做它的对称中心,这两个图形中的对应点,叫做关于对称中心的对称点。
课堂小结
二.中心对称的性质
如果两个图形的对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形一定关于这一点成中心对称.
在成中心对称的两个图形中,连结对称点的线段都经过对称中心,并且被对称中心平分。
作业与课外学习任务
1.练习作业:书面课本P131 练习 1-2
书面课本P132 习题10.4 4,5
2.课外学习任务:
预习P133 10.5 图形的全等
教学反馈:
作业存在的主要问题:
