2.3.1两条直线的交点坐标 课件(共16张PPT)
文档属性
| 名称 | 2.3.1两条直线的交点坐标 课件(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 756.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-17 10:11:47 | ||
图片预览






文档简介
(共16张PPT)
两条直线的交点坐标
复习提出
当——≠ —— 时,两条直线相交;
A1
A2
B1
B2
当 —— = —— ≠ —— 时,两直线平行;
A1 B1 C1
A2 B2 C2
当 —— = —— = —— 时,两条直线重合。
A1 B1 C1
A2 B2 C2
两条直线A1x+B1y+C1=0和A2x+B2y+C2=0的位置关系与系数的关系?
知识探究(一):两条直线的交点坐标
思考1:若点P在直线l上,则点P的坐标(x0,y0)与直线l的方程Ax+By+C=0有什么关系?
Ax0+By0+C=0
思考2:直线2x+y-1=0与直线2x+y+1=0,直线3x+4y-2=0与直线2x+y+2=0的位置关系分别如何?
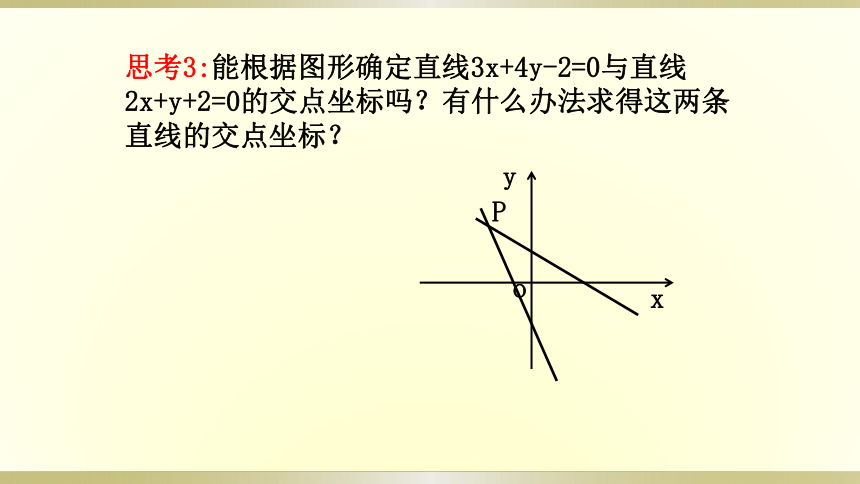
思考3:能根据图形确定直线3x+4y-2=0与直线2x+y+2=0的交点坐标吗?有什么办法求得这两条直线的交点坐标?
x
y
o
P
思考4:一般地,若直线l1:A1x+B1y+C1=0和l2:A2x+B2y+C2=0相交,如何求其交点坐标?
几何元素及关系 代数表示
点A A (a, b)
直线l L:Ax+By+C=0
点A在直线l上
直线l1与l2的交点是A
点A的坐标是方程组的解
Aa+Bb+C=0
(二)讲解新课:
两条直线的交点:
如果两条直线A1x+B1y+C1=0和A2x+B2y+C2=0相交,由于交点同时在两条直线上,交点坐标一定
是它们的方程组成的方程组
的解;反之,如果方程组
只有一个解,那么以这个解为坐标的点就是直线A1x+B1y+C1=0和A2x+B2y+C2=0的交点。
A1x+B1y+C1=0
A2x+B2y+C2=0
A1x+B1y+C1=0
A2x+B2y+C2=0
思考5:对于两条直线 和 ,若方程组
有惟一解,有无数组解,无解,则两直线的位置关系如何?
直线l1、l2联立得方程组
(代数问题) (几何问题)
一般地,对于直线l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0(A1B1C1≠0,A2B2C2≠0),有 方程组
例1:求下列两条直线的交点:
l1:3x+4y-2=0; l2:2x+y+2=0.
解:解方程组
3x+4y-2 =0
2x+y+2 = 0
∴l1与l2的交点是M(- 2,2)
x= -2
y=2
得
例2 判断下列各对直线的位置关系,如果相交,求出其交点的坐标.
(1)
(2)
(3)
例3:求直线3x+2y-1=0和2x-3y-5=0的交点M的坐标,并证明方程3x+2y-1+y(2x-3y-5)=0(y为任意常数)表示过M点的所有直线(不包括直线2x-3y-5=0)。
证明:联立方程
3x+2y-1=0
2x-3y-5=0
o
x
y
(1, - 1)
M
解得:
x=1
y= - 1
代入:x+2y-1+y(2x-3y-5)= 0
得 0+y·0=0
∴M点在直线上
A1x+B1y+C1+y( A2x+B2y+C2)=0是过直A1x+B1y+C1=0和A2x+B2y+C2=0的交点的直线系方程。
M(1,- 1)
即
知识探究(二):过交点的直线系
思考1:经过直线l1:3x+4y-2=0与直线l2:2x+y+2=0的交点可作无数条直线,你能将这些直线的方程统一表示吗?
k存在: y-2=k(x+2);k不存在: x=-2 思考2:上述直线l1与直线l2的交点M(-2,2)在这条直线上吗?当m,n为何值时,方程
分别表示直线l1和l2?
n=0,m=o分别表示直线l1和l2
表示一些直线
思考4:方程 表示的直线包括过交点M(-2,2)的所有直线吗?
思考3:方程 (m,n不同时为0)表示什么图形?
不表示2x+y+2=0这条直线
思考5:方程 表示经过直线l1和l2的交点的直线系,一般地,经过两相交直线l1:A1x+B1y+C1=0和l2:A2x+B2y+C2=0的交点的直线系方程可怎样表示?
m(A1x+B1y+C1)+n(A2x+B2y+C2)=0
或A1x+B1y+C1+y( A2x+B2y+C2)=0
例4:求经过两条直线x+2y-1=0和2x-y-7=0的交点,
且垂直于直线x+3y-5=0的直线方程。
解法一:解方程组
x+2y-1=0,
2x-y-7=0
得
x=3
y= -1
∴这两条直线的交点坐标为(3,-1)
又∵直线x+2y-5=0的斜率是-1/3
∴所求直线的斜率是3
所求直线方程为y+1=3(x-3)即 3x-y-10=0
解法二:所求直线在直线系2x-y-7+y(x+2y-1)=0中
经整理,可得(2+y)x+(2λ-1)y-yλ-7=0
∴ - ———— =3
2+y
2y-1
解得 y= 1/7
因此,所求直线方程为3x-y-10=0
例5:
求证:不论m取何实数,直线(2m-1)x-(m+3)y-(m-11)=0恒过一个定点,并求出此定点的坐标.
1)对于直线l1:A1x+B1y+C1=0 , l2:A2x+B2y+C2=0
(A1B1C1≠0,A2B2C2≠0),有方程组
小结:
2)过交点的直线系经过两相交直线l1:A1x+B1y+C1=0和l2:A2x+B2y+C2=0的交点的直线系方程可表示
m(A1x+B1y+C1)+n(A2x+B2y+C2)=0
或A1x+B1y+C1+y( A2x+B2y+C2)=0
两条直线的交点坐标
复习提出
当——≠ —— 时,两条直线相交;
A1
A2
B1
B2
当 —— = —— ≠ —— 时,两直线平行;
A1 B1 C1
A2 B2 C2
当 —— = —— = —— 时,两条直线重合。
A1 B1 C1
A2 B2 C2
两条直线A1x+B1y+C1=0和A2x+B2y+C2=0的位置关系与系数的关系?
知识探究(一):两条直线的交点坐标
思考1:若点P在直线l上,则点P的坐标(x0,y0)与直线l的方程Ax+By+C=0有什么关系?
Ax0+By0+C=0
思考2:直线2x+y-1=0与直线2x+y+1=0,直线3x+4y-2=0与直线2x+y+2=0的位置关系分别如何?
思考3:能根据图形确定直线3x+4y-2=0与直线2x+y+2=0的交点坐标吗?有什么办法求得这两条直线的交点坐标?
x
y
o
P
思考4:一般地,若直线l1:A1x+B1y+C1=0和l2:A2x+B2y+C2=0相交,如何求其交点坐标?
几何元素及关系 代数表示
点A A (a, b)
直线l L:Ax+By+C=0
点A在直线l上
直线l1与l2的交点是A
点A的坐标是方程组的解
Aa+Bb+C=0
(二)讲解新课:
两条直线的交点:
如果两条直线A1x+B1y+C1=0和A2x+B2y+C2=0相交,由于交点同时在两条直线上,交点坐标一定
是它们的方程组成的方程组
的解;反之,如果方程组
只有一个解,那么以这个解为坐标的点就是直线A1x+B1y+C1=0和A2x+B2y+C2=0的交点。
A1x+B1y+C1=0
A2x+B2y+C2=0
A1x+B1y+C1=0
A2x+B2y+C2=0
思考5:对于两条直线 和 ,若方程组
有惟一解,有无数组解,无解,则两直线的位置关系如何?
直线l1、l2联立得方程组
(代数问题) (几何问题)
一般地,对于直线l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0(A1B1C1≠0,A2B2C2≠0),有 方程组
例1:求下列两条直线的交点:
l1:3x+4y-2=0; l2:2x+y+2=0.
解:解方程组
3x+4y-2 =0
2x+y+2 = 0
∴l1与l2的交点是M(- 2,2)
x= -2
y=2
得
例2 判断下列各对直线的位置关系,如果相交,求出其交点的坐标.
(1)
(2)
(3)
例3:求直线3x+2y-1=0和2x-3y-5=0的交点M的坐标,并证明方程3x+2y-1+y(2x-3y-5)=0(y为任意常数)表示过M点的所有直线(不包括直线2x-3y-5=0)。
证明:联立方程
3x+2y-1=0
2x-3y-5=0
o
x
y
(1, - 1)
M
解得:
x=1
y= - 1
代入:x+2y-1+y(2x-3y-5)= 0
得 0+y·0=0
∴M点在直线上
A1x+B1y+C1+y( A2x+B2y+C2)=0是过直A1x+B1y+C1=0和A2x+B2y+C2=0的交点的直线系方程。
M(1,- 1)
即
知识探究(二):过交点的直线系
思考1:经过直线l1:3x+4y-2=0与直线l2:2x+y+2=0的交点可作无数条直线,你能将这些直线的方程统一表示吗?
k存在: y-2=k(x+2);k不存在: x=-2 思考2:上述直线l1与直线l2的交点M(-2,2)在这条直线上吗?当m,n为何值时,方程
分别表示直线l1和l2?
n=0,m=o分别表示直线l1和l2
表示一些直线
思考4:方程 表示的直线包括过交点M(-2,2)的所有直线吗?
思考3:方程 (m,n不同时为0)表示什么图形?
不表示2x+y+2=0这条直线
思考5:方程 表示经过直线l1和l2的交点的直线系,一般地,经过两相交直线l1:A1x+B1y+C1=0和l2:A2x+B2y+C2=0的交点的直线系方程可怎样表示?
m(A1x+B1y+C1)+n(A2x+B2y+C2)=0
或A1x+B1y+C1+y( A2x+B2y+C2)=0
例4:求经过两条直线x+2y-1=0和2x-y-7=0的交点,
且垂直于直线x+3y-5=0的直线方程。
解法一:解方程组
x+2y-1=0,
2x-y-7=0
得
x=3
y= -1
∴这两条直线的交点坐标为(3,-1)
又∵直线x+2y-5=0的斜率是-1/3
∴所求直线的斜率是3
所求直线方程为y+1=3(x-3)即 3x-y-10=0
解法二:所求直线在直线系2x-y-7+y(x+2y-1)=0中
经整理,可得(2+y)x+(2λ-1)y-yλ-7=0
∴ - ———— =3
2+y
2y-1
解得 y= 1/7
因此,所求直线方程为3x-y-10=0
例5:
求证:不论m取何实数,直线(2m-1)x-(m+3)y-(m-11)=0恒过一个定点,并求出此定点的坐标.
1)对于直线l1:A1x+B1y+C1=0 , l2:A2x+B2y+C2=0
(A1B1C1≠0,A2B2C2≠0),有方程组
小结:
2)过交点的直线系经过两相交直线l1:A1x+B1y+C1=0和l2:A2x+B2y+C2=0的交点的直线系方程可表示
m(A1x+B1y+C1)+n(A2x+B2y+C2)=0
或A1x+B1y+C1+y( A2x+B2y+C2)=0
