人教版七年级下册 6.1 方根 课件(共26张PPT)
文档属性
| 名称 | 人教版七年级下册 6.1 方根 课件(共26张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 938.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-18 00:00:00 | ||
图片预览







文档简介
(共26张PPT)
第2课时
6.1 平方根
1.什么叫做算术平方根?
2.判断下列各数有没有算术平方根,如果有请求出它们的算术平方根.
100; 1; 0; -0.0025; (-3)2 ; -25;
一般地,如果一个正数 x 的平方等于a,即x2=a,那么这个正数x叫做a的算术平方根. a的算术平方根记为 ,读作“ 根号 a” .
10; 1; 0; 无; 3 ; 无;
(1)32= ,(-3)2= ;
(2) , ;
(3)0.82= (-0.8)2= .
9
0.64
0.64
3. 填空
9
思考:反过来,如果已知一个数的平方,怎样求这个数?
1.掌握平方根的概念,明确平方根和算术平方根之间的联系和区别.
2.能用符号正确地表示一个数的平方根,理解开平方运算和乘方运算之间的互逆关系.
问题 如果一个数的平方等于9,这个数是多少?
想一想:3和-3有什么特征?
由于 ,
所以这个数是3或-3.
3和-3互为相反数,会不会是巧合呢
根据上面的研究过程填表:
如果我们把 分别叫做
的平方根,你能给出平方根的概念吗?
根据上述问题,即要找出一个数,使它的平方等于给定的数.由此我们抽象出下述概念:
如果有一个数x,使得x2=a,那么我们把x叫作a的一个平方根,也叫作二次方根.
如果x是正数a的一个平方根,那么a的平方根有且只有两个:x与-x.即平方根互为相反数.
平方根的性质:
例如: (±1)2=1,1的平方根为±1.
平方根的概念
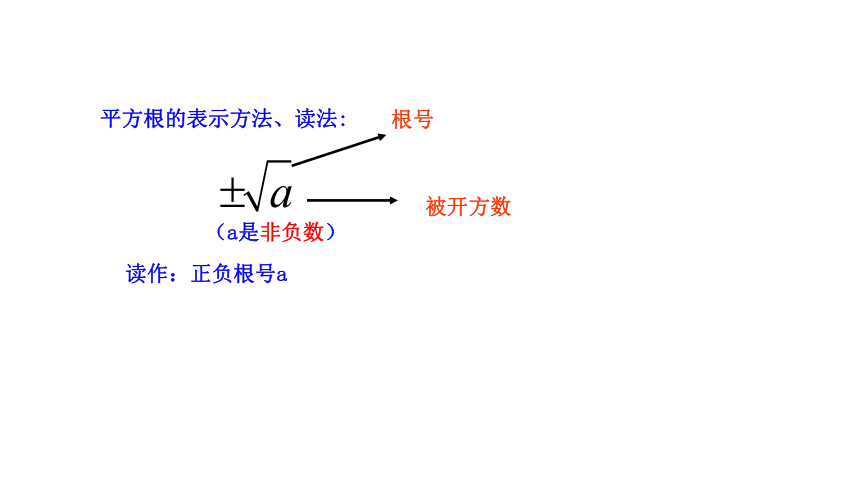
平方根的表示方法、读法:
根号
被开方数
(a是非负数)
读作:正负根号a
由于02=0,而非零数的平方不等于0,因此零的平方根就是0本身.
由于同号两数相乘得正数,所以任何一个数的平方都不会是负数,因此-9没有平方根,进一步的,所有的负数都没有平方根.
在上面的问题中,我们求平方根的数都是正数.
1.零有平方根吗?如果有,它的平方根是多少?
2.-9有平方根吗?负数有平方根吗
1.一个正数有两个平方根,它们互为相反数;
2.零的平方根是0;
3.负数没有平方根.
平方根的性质:
【例1】求下列各数的平方根:
(1)25 (2)0.81 (3)15
(4)(-2) (5)0 (6)-3
【例题】
【解析】(1)因为 ,所以25的平方根是±5,即
(2)因为 ,所以0.81的平方根是±0.9,即
(3)15的平方根是±
(4)因为 ,所以 的平方根是±2,即
(5)0的平方根是0.
(6)-3没有平方根.
求下列各数的平方根:
(1)81; (2) ; (3)0.49.
解:(1)∵(±9)2=81,
(3)∵(±0.7)2=0.49,
∴0.49的平方根为±0.7,
∴81的平方根为±9,
即 .
(2)
的平方根是 ,
即 .
即 .
【跟踪训练】
+1
-1
+2
-2
+3
-3
1
4
9
平方
已知一个数,求它的平方的运算,叫作平方运算.
平方与开方的关系
+1
-1
+2
-2
+3
-3
1
4
9
?运算
反之,已知一个数的平方,求这个数的运算是什么?
求一个数的平方根的运算叫作开平方.
开平方与平方是什么关系?
a的平方根
底数
幂
被开方数
互为
逆运算
指数
根号
已知底数和指数求幂
已知幂和指数求底数
开平方运算
平方运算
开平方与平方的对比填空
正数与零
任何数
幂
平方根
开方
平方
运算符号
适用范围
运算结果名称
性质
正数有 个平方根,它们 ,
零的平方根是 ,
负数 .
正数的平方是 数; 零的平方是 ; 负数的平方是 数.
正
正
0
2
互为相反数
0
没有平方根
1.包含关系:平方根包含算术平方根,算术平方根是平方根的一种.
平方根与算术平方根的联系与区别:
2.只有非负数才有平方根和算术平方根.
3. 0的平方根是0,算术平方根也是0.
区别:
1.个数不同:一个正数有两个平方根,
但只有一个算术平方根.
联系:
2.表示法不同:平方根表示为:
而算术平方根表示为 .
例2 求下列各式的值:
解:(1) ;
(2) ;
(3) .
(1)
(2)
(3)
【例题】
1.下列各式有意义吗?
±
(3) ;
2.求下列各式的值.
(4) .
(1) ;
(2) ;
有意义
有意义
有意义
无意义
【跟踪训练】
1.掌握平方根的概念,明确平方根和算术平方根之间的联系和区别.
2.能用符号正确地表示一个数的平方根,理解开平方运算和乘方运算之间的互逆关系.
1.(杭州·中考)4的平方根是( )
A.2 B. 2 C.16 D. 16
【解析】4的平方根是 .
B
2.(黄冈·中考)2的平方根是_________.
【解析】根据平方根的定义得出2的平方根是± .
±
3.一个数x的平方根等于m+1和m-3,则m= ,x= .
【解析】根据一个正数的平方根互为相反数得,m+1和
m-3互为相反数,即m+1+m-3=0,解得m=1,则m+1=2,
m-3=-2,所以x=4.
1 4
4.若|a-9|+(b-4) =0,则 的平方根是____.
【解析】因为|a-9|和(b-4) 都是非负数,且|a-9|+
(b-4) =0,所以|a-9|=0,(b-4) =0,所以a=9,b=4,
,其平方根为
5. 你能求出下列各式中的未知数x吗?
(1)x2=49.
(2)(x-1)2=25.
【解析】(1)x=±7.
(2)x=6或x=-4.
第2课时
6.1 平方根
1.什么叫做算术平方根?
2.判断下列各数有没有算术平方根,如果有请求出它们的算术平方根.
100; 1; 0; -0.0025; (-3)2 ; -25;
一般地,如果一个正数 x 的平方等于a,即x2=a,那么这个正数x叫做a的算术平方根. a的算术平方根记为 ,读作“ 根号 a” .
10; 1; 0; 无; 3 ; 无;
(1)32= ,(-3)2= ;
(2) , ;
(3)0.82= (-0.8)2= .
9
0.64
0.64
3. 填空
9
思考:反过来,如果已知一个数的平方,怎样求这个数?
1.掌握平方根的概念,明确平方根和算术平方根之间的联系和区别.
2.能用符号正确地表示一个数的平方根,理解开平方运算和乘方运算之间的互逆关系.
问题 如果一个数的平方等于9,这个数是多少?
想一想:3和-3有什么特征?
由于 ,
所以这个数是3或-3.
3和-3互为相反数,会不会是巧合呢
根据上面的研究过程填表:
如果我们把 分别叫做
的平方根,你能给出平方根的概念吗?
根据上述问题,即要找出一个数,使它的平方等于给定的数.由此我们抽象出下述概念:
如果有一个数x,使得x2=a,那么我们把x叫作a的一个平方根,也叫作二次方根.
如果x是正数a的一个平方根,那么a的平方根有且只有两个:x与-x.即平方根互为相反数.
平方根的性质:
例如: (±1)2=1,1的平方根为±1.
平方根的概念
平方根的表示方法、读法:
根号
被开方数
(a是非负数)
读作:正负根号a
由于02=0,而非零数的平方不等于0,因此零的平方根就是0本身.
由于同号两数相乘得正数,所以任何一个数的平方都不会是负数,因此-9没有平方根,进一步的,所有的负数都没有平方根.
在上面的问题中,我们求平方根的数都是正数.
1.零有平方根吗?如果有,它的平方根是多少?
2.-9有平方根吗?负数有平方根吗
1.一个正数有两个平方根,它们互为相反数;
2.零的平方根是0;
3.负数没有平方根.
平方根的性质:
【例1】求下列各数的平方根:
(1)25 (2)0.81 (3)15
(4)(-2) (5)0 (6)-3
【例题】
【解析】(1)因为 ,所以25的平方根是±5,即
(2)因为 ,所以0.81的平方根是±0.9,即
(3)15的平方根是±
(4)因为 ,所以 的平方根是±2,即
(5)0的平方根是0.
(6)-3没有平方根.
求下列各数的平方根:
(1)81; (2) ; (3)0.49.
解:(1)∵(±9)2=81,
(3)∵(±0.7)2=0.49,
∴0.49的平方根为±0.7,
∴81的平方根为±9,
即 .
(2)
的平方根是 ,
即 .
即 .
【跟踪训练】
+1
-1
+2
-2
+3
-3
1
4
9
平方
已知一个数,求它的平方的运算,叫作平方运算.
平方与开方的关系
+1
-1
+2
-2
+3
-3
1
4
9
?运算
反之,已知一个数的平方,求这个数的运算是什么?
求一个数的平方根的运算叫作开平方.
开平方与平方是什么关系?
a的平方根
底数
幂
被开方数
互为
逆运算
指数
根号
已知底数和指数求幂
已知幂和指数求底数
开平方运算
平方运算
开平方与平方的对比填空
正数与零
任何数
幂
平方根
开方
平方
运算符号
适用范围
运算结果名称
性质
正数有 个平方根,它们 ,
零的平方根是 ,
负数 .
正数的平方是 数; 零的平方是 ; 负数的平方是 数.
正
正
0
2
互为相反数
0
没有平方根
1.包含关系:平方根包含算术平方根,算术平方根是平方根的一种.
平方根与算术平方根的联系与区别:
2.只有非负数才有平方根和算术平方根.
3. 0的平方根是0,算术平方根也是0.
区别:
1.个数不同:一个正数有两个平方根,
但只有一个算术平方根.
联系:
2.表示法不同:平方根表示为:
而算术平方根表示为 .
例2 求下列各式的值:
解:(1) ;
(2) ;
(3) .
(1)
(2)
(3)
【例题】
1.下列各式有意义吗?
±
(3) ;
2.求下列各式的值.
(4) .
(1) ;
(2) ;
有意义
有意义
有意义
无意义
【跟踪训练】
1.掌握平方根的概念,明确平方根和算术平方根之间的联系和区别.
2.能用符号正确地表示一个数的平方根,理解开平方运算和乘方运算之间的互逆关系.
1.(杭州·中考)4的平方根是( )
A.2 B. 2 C.16 D. 16
【解析】4的平方根是 .
B
2.(黄冈·中考)2的平方根是_________.
【解析】根据平方根的定义得出2的平方根是± .
±
3.一个数x的平方根等于m+1和m-3,则m= ,x= .
【解析】根据一个正数的平方根互为相反数得,m+1和
m-3互为相反数,即m+1+m-3=0,解得m=1,则m+1=2,
m-3=-2,所以x=4.
1 4
4.若|a-9|+(b-4) =0,则 的平方根是____.
【解析】因为|a-9|和(b-4) 都是非负数,且|a-9|+
(b-4) =0,所以|a-9|=0,(b-4) =0,所以a=9,b=4,
,其平方根为
5. 你能求出下列各式中的未知数x吗?
(1)x2=49.
(2)(x-1)2=25.
【解析】(1)x=±7.
(2)x=6或x=-4.
