人教版七年级下册 10.2 直方图 课件(共31张PPT)
文档属性
| 名称 | 人教版七年级下册 10.2 直方图 课件(共31张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-18 00:00:00 | ||
图片预览










文档简介
(共31张PPT)
10.2 直方图
身高/㎝
7
6
5
4
3
2
1
0
149 152 155 158 161 164 167 170 173
频数/组距
1.了解频数、直方图的概念。
2.明确频数直方图制作的步骤,会绘制频数直方图。
3.能从频数分布表和频数直方图中获取有关信息,作出合理的判断和预测。
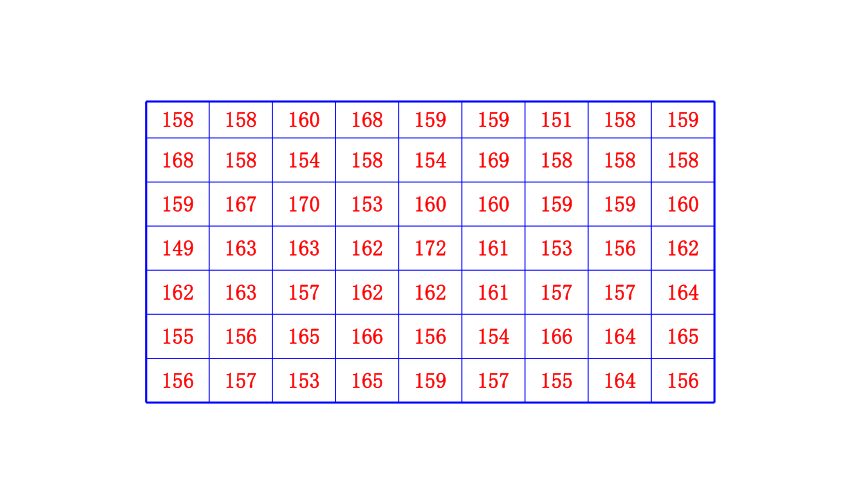
为了参加全校各个年级之间的广播操比赛,七年级准备从63名同学中挑出身高相差不多的40名同学参加比赛.为此收集到这63名同学的身高(单位:cm)如下:
158 158 160 168 159 159 151 158 159
168 158 154 158 154 169 158 158 158
159 167 170 153 160 160 159 159 160
149 163 163 162 172 161 153 156 162
162 163 157 162 162 161 157 157 164
155 156 165 166 156 154 166 164 165
156 157 153 165 159 157 155 164 156
为了使选取的参赛选手身高比较整齐,需要知道数据(身高)的分布情况,即在哪些身高范围内的学生人数比较多,哪些身高范围内的学生人数比较少.为此可以通过对这些数据适当分组来进行整理.
选择身高在哪个范围内的学生参加呢?
1.计算最大值和最小值的差
在上面的数据中,最小值是149,最大值是172,它们的差是23,说明身高的变化范围是0~23 cm.
2.决定组距和组数
把所有数据分成若干组,每个小组的两个端点之间的距离(组内数据的取值范围)称为组距.
所以要将数据分成8组:149≤x<152,152≤x<155,… 170≤x<173.这里组数和组距分别为8和3.
3.列频数分布表
对落在各个小组内的数据进行累计,得到各个小组内的数据的个数(叫做频数).整理可以得到频数分布表,见教材146页表10-3.
从表中可以看出,身高在155≤x<158,158≤x<161,161≤x<164三个组的人数最多,一共有41人,因此可以从身高在155 cm~164 cm(不含164 cm)的学生中选队员.
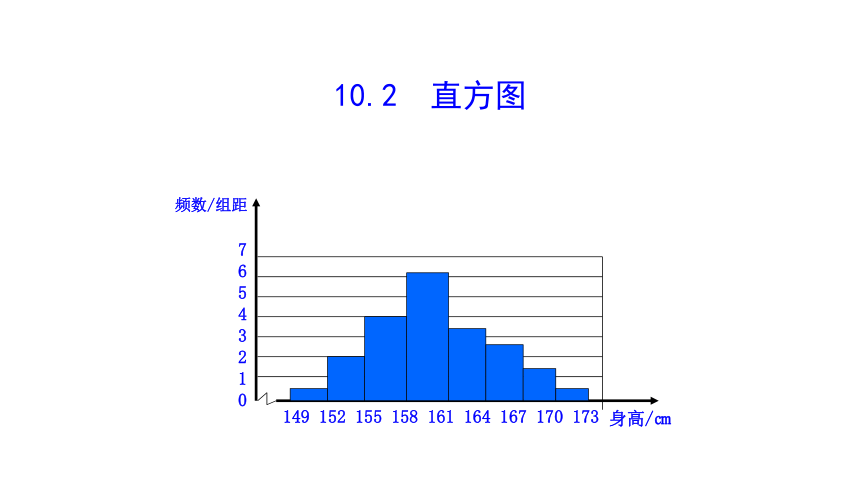
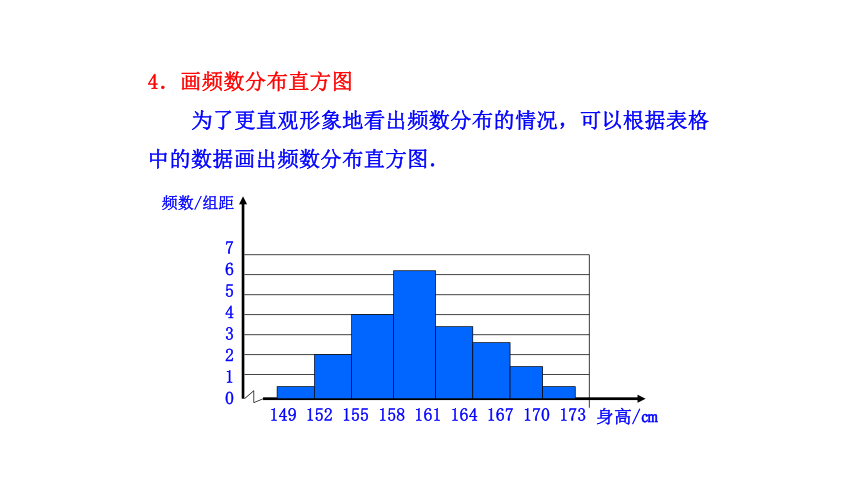
4.画频数分布直方图
为了更直观形象地看出频数分布的情况,可以根据表格中的数据画出频数分布直方图.
身高/㎝
7
6
5
4
3
2
1
0
149 152 155 158 161 164 167 170 173
频数/组距
条形统计图与频数直方图有什么区别和联系?
(1)联系——用途都是可以直观地表示出具体数量.频数直方图是特殊的条形统计图.
(3)绘制的形式不同——条形统计图各条形分开;频数直方图的条形连在一起.
(2)区别——条形统计图是直观地显示出具体数据;频数直方图是表现频数的分布情况.
制作频数直方图的大致步骤:
(1)找出所给数据中的最大值和最小值,求最大值与最小值的差确定统计量的范围.
(4)根据分组和频数,绘制频数直方图.
(3)统计每组中数据的频数.
(2)确定组数和组距并进行分组.(数据个数在100以内,一般分5至12组)
频数分布直方图是以小长方形的面积来反映数据落在各个小组内的频数的大小.小长方形的高是频数与组距的比值.
等距分组时,各小长方形的面积(频数)与高的比是常数(组距).因此,画等距分组的频数分布直方图时,为画图与看图方便,通常直接用小长方形的高表示频数.
【概念学习】
例1 某校一学生社团参加数学实践活动,和交警一起在金山大道入口用移动测速仪监测一组汽车通过的时速(千米/时),在数据整理统计绘制频数直方图的过程中,不小心墨汁将表中的部分数据污染(见下表),请根据下面不完整的频数分布表和频数直方图,解答问题:(注:50~60指时速大于等于50千米/时而小于60千米/时,其他类同)
【例题】
(1)请用你所学的数学统计知识,补全频数直方图;
39
数据段 “正”字记录 频数
50~60 正正正正正正
60~70 正正正正正正正
70~80 正正正正正正正正正正正正正正 74
80~90 正正正
90~100 正正正正
合计 185
社会实践调查记载表
(2)如果此地汽车时速不低于80千米/时即为违章,求这组汽车的违章频数;
(3)如果请你根据调查数据绘制扇形统计图,那么时速在70~80范围内的车辆数所对应的扇形圆心角的度数是________.
解:18+22=40.
144°
为了解某校九年级男生的身高情况,该校从九年级随机找来50名男生进行了身高测量,根据测量结果(均取整数,单位:cm)列出了下表.
根据表中提供的信息回答下列问题:
(1)数据在161~165范围内的频数是_____;
(2)频数最大的一组数据的范围是________;
(3)估计该校九年级男生身高在176cm(包括176cm)以上的约占____%.
12
166~170
12
分组 频数
151~155 3
156~160 4
161~165 12
166~170 13
171~175 12
176~180 4
181以上 2
合计 50
【跟踪训练】
例2 为了了解某地区新生儿体重状况,某医院随机调取了该地区60名新生儿出生体重,结果(单位:克)如下:
3850 3900 3300 3500 3315 3800 2550 3800 4150 2500 2700 2850 3800 3500 2900 2850 3300 3650 4000 3300 2800 2150 3700 3465 3680 2900 3050 3850 3610 3800 3280 3100 3000 2800 3500 4050 3300 3450 3100 3400 4160 3300 2750 3250 2350 3520 3850 2850 3450 3800 3500 3100 1900 3200 3400 3400 3400 3120 3600 2900
【例题】
将数据适当分组,并绘制相应的频数直方图,从图中反映出该地区新生儿体重状况怎样?
解:(1)确定所给数据的最大值和最小值:上述数据中最
小值是1900,最大值是4160;
(2)将数据适当分组:最大值和最小值相差
4160-1900=2260,考虑以250为组距,
2260÷250=9.04,可以考虑分成10组;
(3)统计每组中数据出现的次数(频数)
分组 人数 分组 人数
1750~2000 3000~3250
2000~2250 3250~3500
2250~2500 3500~3750
2500~2750 3750~4000
2750~3000 4000~4250
1
1
1
3
9
7
14
11
9
4
(4)绘制频数直方图
从图中可以看出该地区新生儿体重在3250~3500g的人数最多.
4250
银行在某储蓄所抽样调查了50名顾客,他们的等待时间(进入银行到接受受理的时间间隔,单位:min)如下:
15 20 18 3 25 34 6 0 17 24 23 30 35 42 37 24 21 1 14 12 34 22 13 34 8 22 31 24 17 33 4 14 23 32 33 28 42 25 14 22 31 42 34 26 14 25 40 14 24 11
将数据适当分组,并绘制相应的频数直方图.
解:(1)最大值与最小值的差:42-0=42;(2)组距是7时,42÷7=6,则分成6组;
等待时间:min 划记 频数
0≤x<7 4
7≤x<14 4
14≤x<21 正正
21≤x<28 正正 12
28≤x<35 正正 11
35≤x≤42 正 9
合计 50
表1
(3)如表1所示;
(4)如图1所示.
图1
12
10
8
6
4
2
10
频数直方图
用频数直方图表示数据
制作频数直方图
1.计算最大值与最小值的差
2.确定组数和组距并进行分组
3.统计每组中数据的频数
4.绘制频数直方图
从频数直方图获取信息
1.如图所示的是某校初一学生到校方式的条形统计图, 根据图形可得出骑自行车人数占初一总人数的_______%.
【解析】
30
2.(湖州·中考)某校欲举办“校园吉尼斯挑战赛”,为此该校在三个年级中各随机抽取一个班级进行了一次“你最喜欢的挑战项目”的问卷调查,每名学生都选了一项.已知被调查的三个年级的学生人数均为50人,根据收集到的数据,绘制成如下统计图表(不完整):
根据统计图表中的信息,解答下列问题:
(1)在本次随机调查中,七年级抽查班级中喜欢“跳绳”项目的学生有_________ 人,九年级抽查班级中喜欢“乒乓球”项目的学生人数占本班人数的百分比为_________.
(2)请将条形统计图补充完整.
(3)若该校共有900名学生(三个年级的学生人数都相等),请你估计该校喜欢“羽毛球”项目的学生总人数.
【解析】(1)七年级抽查班级中喜欢“跳绳”项目的学生为:
50-14-10-8-6=12(人).九年级抽查班级中喜欢“乒乓球”项目
的学生人数占本班人数的百分比为1-20%-16%-28%-18%=18%.
(2)八年级最喜欢“踢毽子”项目的人数为50-18-9-9-7=7.
(3)900× =162,该校喜欢“羽毛球”项目的学生总人数
约为162人.
【答案】
(1)12 18%
(2)如图所示
(3)该校喜欢“羽毛球”项目的学生总人数约为162人
3.学习了统计知识后,小刚就本班同学的上学方式进行了一次调查统计,图①和图②是他通过采集数据后,绘制的两幅不完整的统计图.请你根据图中提供的信息,解答以下问题:
(1)求该班共有多少名学生?
图①
图②
【解析】(1)看条形统计图知乘车上学的有20人,这20人占全班总人数的百分比是50% (由扇形统计图可以知道),所以全班总人数是:20÷50%=40(人) .
3.学习了统计知识后,小刚就本班同学的上学方式进行了一次调查统计,图①和图②是他通过采集数据后,绘制的两幅不完整的统计图.请你根据图中提供的信息,解答以下问题:
(2)在图①中,将表示“步行”的部分补充完整.
图①
图②
(2)看扇形统计图可知,步行上学的人占总人数的20%,总人数为40人,所以步行上学的人数是:40×20%=8(人) ;补全的图形如上:
3.学习了统计知识后,小刚就本班同学的上学方式进行了一次调查统计,图①和图②是他通过采集数据后,绘制的两幅不完整的统计图.请你根据图中提供的信息,解答以下问题:
(3)在扇形统计图中,计算出“骑车”部分所对应的圆心角的度数.
图①
图②
(3)看扇形统计图知,“骑车”部分的百分比是:
1-50%-20%=30%,“骑车”部分所对应的圆心角的度数为360°×30%=108°.
3.学习了统计知识后,小刚就本班同学的上学方式进行了一次调查统计,图①和图②是他通过采集数据后,绘制的两幅不完整的统计图.请你根据图中提供的信息,解答以下问题:
(4)如果全年级共500名同学,请你估算全年级步行上学的学生人数.
图①
图②
(4)步行上学的人数占的百分比是20%,全年级500人,所以,估算全年级步行上学的人数是500×20%=100(人).
10.2 直方图
身高/㎝
7
6
5
4
3
2
1
0
149 152 155 158 161 164 167 170 173
频数/组距
1.了解频数、直方图的概念。
2.明确频数直方图制作的步骤,会绘制频数直方图。
3.能从频数分布表和频数直方图中获取有关信息,作出合理的判断和预测。
为了参加全校各个年级之间的广播操比赛,七年级准备从63名同学中挑出身高相差不多的40名同学参加比赛.为此收集到这63名同学的身高(单位:cm)如下:
158 158 160 168 159 159 151 158 159
168 158 154 158 154 169 158 158 158
159 167 170 153 160 160 159 159 160
149 163 163 162 172 161 153 156 162
162 163 157 162 162 161 157 157 164
155 156 165 166 156 154 166 164 165
156 157 153 165 159 157 155 164 156
为了使选取的参赛选手身高比较整齐,需要知道数据(身高)的分布情况,即在哪些身高范围内的学生人数比较多,哪些身高范围内的学生人数比较少.为此可以通过对这些数据适当分组来进行整理.
选择身高在哪个范围内的学生参加呢?
1.计算最大值和最小值的差
在上面的数据中,最小值是149,最大值是172,它们的差是23,说明身高的变化范围是0~23 cm.
2.决定组距和组数
把所有数据分成若干组,每个小组的两个端点之间的距离(组内数据的取值范围)称为组距.
所以要将数据分成8组:149≤x<152,152≤x<155,… 170≤x<173.这里组数和组距分别为8和3.
3.列频数分布表
对落在各个小组内的数据进行累计,得到各个小组内的数据的个数(叫做频数).整理可以得到频数分布表,见教材146页表10-3.
从表中可以看出,身高在155≤x<158,158≤x<161,161≤x<164三个组的人数最多,一共有41人,因此可以从身高在155 cm~164 cm(不含164 cm)的学生中选队员.
4.画频数分布直方图
为了更直观形象地看出频数分布的情况,可以根据表格中的数据画出频数分布直方图.
身高/㎝
7
6
5
4
3
2
1
0
149 152 155 158 161 164 167 170 173
频数/组距
条形统计图与频数直方图有什么区别和联系?
(1)联系——用途都是可以直观地表示出具体数量.频数直方图是特殊的条形统计图.
(3)绘制的形式不同——条形统计图各条形分开;频数直方图的条形连在一起.
(2)区别——条形统计图是直观地显示出具体数据;频数直方图是表现频数的分布情况.
制作频数直方图的大致步骤:
(1)找出所给数据中的最大值和最小值,求最大值与最小值的差确定统计量的范围.
(4)根据分组和频数,绘制频数直方图.
(3)统计每组中数据的频数.
(2)确定组数和组距并进行分组.(数据个数在100以内,一般分5至12组)
频数分布直方图是以小长方形的面积来反映数据落在各个小组内的频数的大小.小长方形的高是频数与组距的比值.
等距分组时,各小长方形的面积(频数)与高的比是常数(组距).因此,画等距分组的频数分布直方图时,为画图与看图方便,通常直接用小长方形的高表示频数.
【概念学习】
例1 某校一学生社团参加数学实践活动,和交警一起在金山大道入口用移动测速仪监测一组汽车通过的时速(千米/时),在数据整理统计绘制频数直方图的过程中,不小心墨汁将表中的部分数据污染(见下表),请根据下面不完整的频数分布表和频数直方图,解答问题:(注:50~60指时速大于等于50千米/时而小于60千米/时,其他类同)
【例题】
(1)请用你所学的数学统计知识,补全频数直方图;
39
数据段 “正”字记录 频数
50~60 正正正正正正
60~70 正正正正正正正
70~80 正正正正正正正正正正正正正正 74
80~90 正正正
90~100 正正正正
合计 185
社会实践调查记载表
(2)如果此地汽车时速不低于80千米/时即为违章,求这组汽车的违章频数;
(3)如果请你根据调查数据绘制扇形统计图,那么时速在70~80范围内的车辆数所对应的扇形圆心角的度数是________.
解:18+22=40.
144°
为了解某校九年级男生的身高情况,该校从九年级随机找来50名男生进行了身高测量,根据测量结果(均取整数,单位:cm)列出了下表.
根据表中提供的信息回答下列问题:
(1)数据在161~165范围内的频数是_____;
(2)频数最大的一组数据的范围是________;
(3)估计该校九年级男生身高在176cm(包括176cm)以上的约占____%.
12
166~170
12
分组 频数
151~155 3
156~160 4
161~165 12
166~170 13
171~175 12
176~180 4
181以上 2
合计 50
【跟踪训练】
例2 为了了解某地区新生儿体重状况,某医院随机调取了该地区60名新生儿出生体重,结果(单位:克)如下:
3850 3900 3300 3500 3315 3800 2550 3800 4150 2500 2700 2850 3800 3500 2900 2850 3300 3650 4000 3300 2800 2150 3700 3465 3680 2900 3050 3850 3610 3800 3280 3100 3000 2800 3500 4050 3300 3450 3100 3400 4160 3300 2750 3250 2350 3520 3850 2850 3450 3800 3500 3100 1900 3200 3400 3400 3400 3120 3600 2900
【例题】
将数据适当分组,并绘制相应的频数直方图,从图中反映出该地区新生儿体重状况怎样?
解:(1)确定所给数据的最大值和最小值:上述数据中最
小值是1900,最大值是4160;
(2)将数据适当分组:最大值和最小值相差
4160-1900=2260,考虑以250为组距,
2260÷250=9.04,可以考虑分成10组;
(3)统计每组中数据出现的次数(频数)
分组 人数 分组 人数
1750~2000 3000~3250
2000~2250 3250~3500
2250~2500 3500~3750
2500~2750 3750~4000
2750~3000 4000~4250
1
1
1
3
9
7
14
11
9
4
(4)绘制频数直方图
从图中可以看出该地区新生儿体重在3250~3500g的人数最多.
4250
银行在某储蓄所抽样调查了50名顾客,他们的等待时间(进入银行到接受受理的时间间隔,单位:min)如下:
15 20 18 3 25 34 6 0 17 24 23 30 35 42 37 24 21 1 14 12 34 22 13 34 8 22 31 24 17 33 4 14 23 32 33 28 42 25 14 22 31 42 34 26 14 25 40 14 24 11
将数据适当分组,并绘制相应的频数直方图.
解:(1)最大值与最小值的差:42-0=42;(2)组距是7时,42÷7=6,则分成6组;
等待时间:min 划记 频数
0≤x<7 4
7≤x<14 4
14≤x<21 正正
21≤x<28 正正 12
28≤x<35 正正 11
35≤x≤42 正 9
合计 50
表1
(3)如表1所示;
(4)如图1所示.
图1
12
10
8
6
4
2
10
频数直方图
用频数直方图表示数据
制作频数直方图
1.计算最大值与最小值的差
2.确定组数和组距并进行分组
3.统计每组中数据的频数
4.绘制频数直方图
从频数直方图获取信息
1.如图所示的是某校初一学生到校方式的条形统计图, 根据图形可得出骑自行车人数占初一总人数的_______%.
【解析】
30
2.(湖州·中考)某校欲举办“校园吉尼斯挑战赛”,为此该校在三个年级中各随机抽取一个班级进行了一次“你最喜欢的挑战项目”的问卷调查,每名学生都选了一项.已知被调查的三个年级的学生人数均为50人,根据收集到的数据,绘制成如下统计图表(不完整):
根据统计图表中的信息,解答下列问题:
(1)在本次随机调查中,七年级抽查班级中喜欢“跳绳”项目的学生有_________ 人,九年级抽查班级中喜欢“乒乓球”项目的学生人数占本班人数的百分比为_________.
(2)请将条形统计图补充完整.
(3)若该校共有900名学生(三个年级的学生人数都相等),请你估计该校喜欢“羽毛球”项目的学生总人数.
【解析】(1)七年级抽查班级中喜欢“跳绳”项目的学生为:
50-14-10-8-6=12(人).九年级抽查班级中喜欢“乒乓球”项目
的学生人数占本班人数的百分比为1-20%-16%-28%-18%=18%.
(2)八年级最喜欢“踢毽子”项目的人数为50-18-9-9-7=7.
(3)900× =162,该校喜欢“羽毛球”项目的学生总人数
约为162人.
【答案】
(1)12 18%
(2)如图所示
(3)该校喜欢“羽毛球”项目的学生总人数约为162人
3.学习了统计知识后,小刚就本班同学的上学方式进行了一次调查统计,图①和图②是他通过采集数据后,绘制的两幅不完整的统计图.请你根据图中提供的信息,解答以下问题:
(1)求该班共有多少名学生?
图①
图②
【解析】(1)看条形统计图知乘车上学的有20人,这20人占全班总人数的百分比是50% (由扇形统计图可以知道),所以全班总人数是:20÷50%=40(人) .
3.学习了统计知识后,小刚就本班同学的上学方式进行了一次调查统计,图①和图②是他通过采集数据后,绘制的两幅不完整的统计图.请你根据图中提供的信息,解答以下问题:
(2)在图①中,将表示“步行”的部分补充完整.
图①
图②
(2)看扇形统计图可知,步行上学的人占总人数的20%,总人数为40人,所以步行上学的人数是:40×20%=8(人) ;补全的图形如上:
3.学习了统计知识后,小刚就本班同学的上学方式进行了一次调查统计,图①和图②是他通过采集数据后,绘制的两幅不完整的统计图.请你根据图中提供的信息,解答以下问题:
(3)在扇形统计图中,计算出“骑车”部分所对应的圆心角的度数.
图①
图②
(3)看扇形统计图知,“骑车”部分的百分比是:
1-50%-20%=30%,“骑车”部分所对应的圆心角的度数为360°×30%=108°.
3.学习了统计知识后,小刚就本班同学的上学方式进行了一次调查统计,图①和图②是他通过采集数据后,绘制的两幅不完整的统计图.请你根据图中提供的信息,解答以下问题:
(4)如果全年级共500名同学,请你估算全年级步行上学的学生人数.
图①
图②
(4)步行上学的人数占的百分比是20%,全年级500人,所以,估算全年级步行上学的人数是500×20%=100(人).
