广东省汕头市潮师高级中学2012-2013学年高二3月月考数学(文)试题
文档属性
| 名称 | 广东省汕头市潮师高级中学2012-2013学年高二3月月考数学(文)试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 145.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-08 00:00:00 | ||
图片预览



文档简介
汕头市潮师高级中学2012-2013学年高二3月月考数学文试题
一、选择题(每小题5分,共50分)
1.已知圆心为C(6,5),且过点B(3,6)的圆的方程为( )
A. B.
C. D.
2.若直线与直线垂直,则的值是( )
A.1 B.2 C.3 D.4
3、长、宽、高分别为4、3、的长方体的外接球的体积为 ( )
A. 3 B. C. D. 9
4.在同一直角坐标系中,表示直线与正确的是( )
A B C D
5.点关于直线的对称点( )
A. B. C. D.
6.给定下列四个命题:
①若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;
②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;
③垂直于同一直线的两条直线相互平行;
④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直。 其中,为真命题的是
A.①和② B.②和③ C.③和④ D.②和④
7、线段AB的长等于它在平面上射影的2倍,则AB所在的直线和平面所成的角为( ).
A. B. C. D.
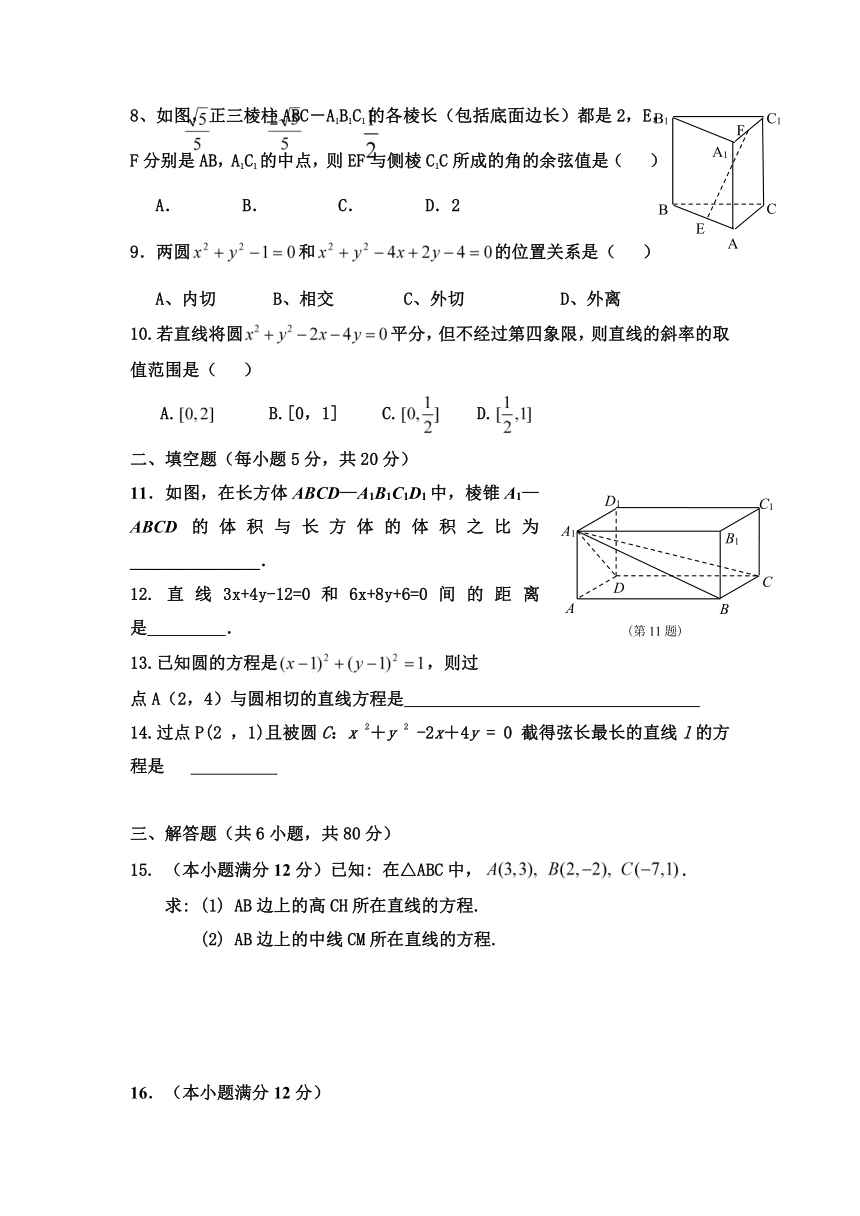
8、如图,正三棱柱ABC-A1B1C1的各棱长(包括底面边长)都是2,E,F分别是AB,A1C1的中点,则EF与侧棱C1C所成的角的余弦值是( )
A. B. C. D.2
9.两圆和的位置关系是( )
A、内切 B、相交 C、外切 D、外离
10.若直线将圆平分,但不经过第四象限,则直线的斜率的取值范围是( )
A. B.[0,1] C. D.
二、填空题(每小题5分,共20分)
11.如图,在长方体ABCD—A1B1C1D1中,棱锥A1—ABCD的体积与长方体的体积之比为_______________.
12.直线3x+4y-12=0和6x+8y+6=0间的距离是 .
13.已知圆的方程是,则过
点A(2,4)与圆相切的直线方程是
14.过点P(2 ,1)且被圆C:x 2+y 2 -2x+4y = 0 截得弦长最长的直线l的方程是
三、解答题(共6小题,共80分)
15. (本小题满分12分)已知: 在△ABC中,.
求: (1) AB边上的高CH所在直线的方程.
(2) AB边上的中线CM所在直线的方程.
16.(本小题满分12分)
已知某几何体的俯视图是如图1所示的矩形,正视图(或称主视图)是一个底边长为8,高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6,高为4的等腰三角形.
(1)求该几何体的体积;
(2)求该几何体的侧面积.
17.( 满分14分)如图所示的四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD, E为PC的中点,求证:
(1)PA∥平面BDE;
(2)平面PAC⊥平面PBD.
18. ( 满分14分)已知圆C的半径为,圆心在直线上,且被直线截得的弦长为,求圆C的方程.
19.( 满分14分)已知为圆上任一点,且点.
(Ⅰ)若在圆上,求线段的长及直线的斜率;
(Ⅱ)求的最大值和最小值;
(Ⅲ)若,求的最大值和最小值.
20.已知半径为5的圆C的圆心在x轴上,圆心的横坐标是整数,且与直线4x+3y-29=0相切.
(1)求圆C的方程;
(2)设直线ax-y+5=0与圆C相交于A,B两点,求实数a的取值范围;
(3) 在(2)的条件下,是否存在实数a,使得过点P(-2,4)的直线l垂直平分弦AB?若存在,求出实数a的值;若不存在,请说明理由.
参考答案
一、选择题:
题号
1
2
3
4
5
6
7
8
9
10
答案
A
A
B
C
D
D
B
A
B
A
二、填空题:
11. 1:3 12. 3
13. x=2或 4x-3y+4=0 14。 3x–y–5 = 0
三、解答题
15【解析】 (1)由已知可求得AB所在直线的斜率,
因为AB⊥CH, 所以,
所以直线CH的方程为: , 整理得:
(2) AB边 的中点M坐标为即为
所以直线CM的方程为: ,
整理得:
17【证明】(1)连接AC交BD于点O,连接OE.
∵四边形ABCD是菱形,∴AO=CO.
∵E为PC的中点,∴EO∥PA.
∵PA平面BDE,EO?平面BDE,
∴PA∥平面BDE.
(2)∵PA⊥平面ABCD,BD?平面ABCD,∴PA⊥BD,
∵四边形ABCD是菱形,∴BD⊥AC.
∵AC∩PA=A,∴BD⊥平面PAC.
∵BD?平面PBD,
∴平面PAC⊥平面PBD.
19【解析】Ⅰ)由点在圆上,
可得,所以.
所以, .
(Ⅱ)由可得.
所以圆心坐标为,半径.
可得,
因此 ,.
(Ⅲ)可知表示直线的斜率,
设直线的方程为:,则.
由直线与圆有交点, 所以 .可得,
所以的最大值为,最小值为.
一、选择题(每小题5分,共50分)
1.已知圆心为C(6,5),且过点B(3,6)的圆的方程为( )
A. B.
C. D.
2.若直线与直线垂直,则的值是( )
A.1 B.2 C.3 D.4
3、长、宽、高分别为4、3、的长方体的外接球的体积为 ( )
A. 3 B. C. D. 9
4.在同一直角坐标系中,表示直线与正确的是( )
A B C D
5.点关于直线的对称点( )
A. B. C. D.
6.给定下列四个命题:
①若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;
②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;
③垂直于同一直线的两条直线相互平行;
④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直。 其中,为真命题的是
A.①和② B.②和③ C.③和④ D.②和④
7、线段AB的长等于它在平面上射影的2倍,则AB所在的直线和平面所成的角为( ).
A. B. C. D.
8、如图,正三棱柱ABC-A1B1C1的各棱长(包括底面边长)都是2,E,F分别是AB,A1C1的中点,则EF与侧棱C1C所成的角的余弦值是( )
A. B. C. D.2
9.两圆和的位置关系是( )
A、内切 B、相交 C、外切 D、外离
10.若直线将圆平分,但不经过第四象限,则直线的斜率的取值范围是( )
A. B.[0,1] C. D.
二、填空题(每小题5分,共20分)
11.如图,在长方体ABCD—A1B1C1D1中,棱锥A1—ABCD的体积与长方体的体积之比为_______________.
12.直线3x+4y-12=0和6x+8y+6=0间的距离是 .
13.已知圆的方程是,则过
点A(2,4)与圆相切的直线方程是
14.过点P(2 ,1)且被圆C:x 2+y 2 -2x+4y = 0 截得弦长最长的直线l的方程是
三、解答题(共6小题,共80分)
15. (本小题满分12分)已知: 在△ABC中,.
求: (1) AB边上的高CH所在直线的方程.
(2) AB边上的中线CM所在直线的方程.
16.(本小题满分12分)
已知某几何体的俯视图是如图1所示的矩形,正视图(或称主视图)是一个底边长为8,高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6,高为4的等腰三角形.
(1)求该几何体的体积;
(2)求该几何体的侧面积.
17.( 满分14分)如图所示的四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD, E为PC的中点,求证:
(1)PA∥平面BDE;
(2)平面PAC⊥平面PBD.
18. ( 满分14分)已知圆C的半径为,圆心在直线上,且被直线截得的弦长为,求圆C的方程.
19.( 满分14分)已知为圆上任一点,且点.
(Ⅰ)若在圆上,求线段的长及直线的斜率;
(Ⅱ)求的最大值和最小值;
(Ⅲ)若,求的最大值和最小值.
20.已知半径为5的圆C的圆心在x轴上,圆心的横坐标是整数,且与直线4x+3y-29=0相切.
(1)求圆C的方程;
(2)设直线ax-y+5=0与圆C相交于A,B两点,求实数a的取值范围;
(3) 在(2)的条件下,是否存在实数a,使得过点P(-2,4)的直线l垂直平分弦AB?若存在,求出实数a的值;若不存在,请说明理由.
参考答案
一、选择题:
题号
1
2
3
4
5
6
7
8
9
10
答案
A
A
B
C
D
D
B
A
B
A
二、填空题:
11. 1:3 12. 3
13. x=2或 4x-3y+4=0 14。 3x–y–5 = 0
三、解答题
15【解析】 (1)由已知可求得AB所在直线的斜率,
因为AB⊥CH, 所以,
所以直线CH的方程为: , 整理得:
(2) AB边 的中点M坐标为即为
所以直线CM的方程为: ,
整理得:
17【证明】(1)连接AC交BD于点O,连接OE.
∵四边形ABCD是菱形,∴AO=CO.
∵E为PC的中点,∴EO∥PA.
∵PA平面BDE,EO?平面BDE,
∴PA∥平面BDE.
(2)∵PA⊥平面ABCD,BD?平面ABCD,∴PA⊥BD,
∵四边形ABCD是菱形,∴BD⊥AC.
∵AC∩PA=A,∴BD⊥平面PAC.
∵BD?平面PBD,
∴平面PAC⊥平面PBD.
19【解析】Ⅰ)由点在圆上,
可得,所以.
所以, .
(Ⅱ)由可得.
所以圆心坐标为,半径.
可得,
因此 ,.
(Ⅲ)可知表示直线的斜率,
设直线的方程为:,则.
由直线与圆有交点, 所以 .可得,
所以的最大值为,最小值为.
同课章节目录
