7.1.2 弧度制 教案

第七章　三角函数
第7.1.2节　弧度制
学生在初中已经学过角的度量单位“度”，并且上节课学了任意角的概念,将角的概念推广到了任意角;本节课作为三角函数的第二课时,实质上还是为后继学习任意角的三角函数作准备,尤其是三角函数的图象，只有把角度转化为弧度，弧度是一个实数，才能在数轴上作出相应的点。因此本节课还起着启下的作用。通过本节弧度制的学习,我们建立起实数与角之间一一对应，而且在弧度制下的弧长公式与扇形面积公式有了更为简单形式。
课程目标 学科素养
1.理解角度制与弧度制的概念，能对弧度和角度进行正确的转换. 2.体会引入弧度制的必要性，建立角的集合与实数集一一对应关系. 3.掌握并能应用弧度制下的扇形弧长公式和面积公式． a数学抽象: 理解角度制与弧度制的概念. b逻辑推理: 能对弧度和角度进行正确的转换. c数学运算: 扇形弧长公式和面积公式的应用.
1.教学重点：能对弧度和角度进行正确的转换.
2.教学难点：扇形弧长公式和面积公式的应用.
1．下列命题正确的是____________(填序号)．
①－30°是第一象限角；
②750°是第四象限角；
③终边相同的角一定相等；
④－950°12′是第二象限的角．
答案：④
2．－1 120°角所在象限是____________．
答案：第四象限
3．与405°角终边相同的角的集合是____________．
答案：{α|α＝k·360°＋45°，k∈Z}
4．在－180°到360°范围内，与2 000°角终边相同的角为____________．
答案：－160°，200°
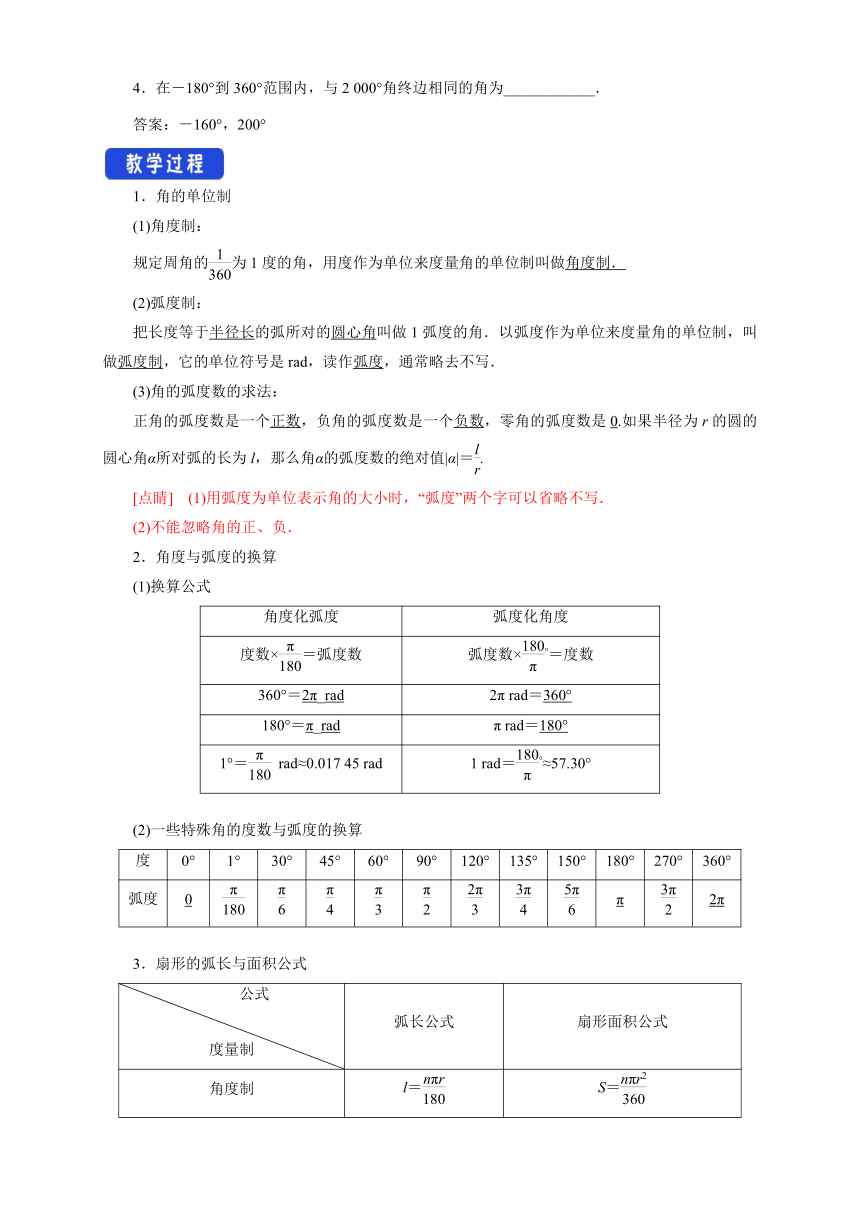
1．角的单位制
(1)角度制：
规定周角的为1度的角，用度作为单位来度量角的单位制叫做角度制．
(2)弧度制：
把长度等于半径长的弧所对的圆心角叫做1弧度的角．以弧度作为单位来度量角的单位制，叫做弧度制，它的单位符号是rad，读作弧度，通常略去不写．
(3)角的弧度数的求法：
正角的弧度数是一个正数，负角的弧度数是一个负数，零角的弧度数是0.如果半径为r的圆的圆心角α所对弧的长为l，那么角α的弧度数的绝对值|α|＝.
[点睛]　(1)用弧度为单位表示角的大小时，“弧度”两个字可以省略不写．
(2)不能忽略角的正、负．
2．角度与弧度的换算
(1)换算公式
角度化弧度 弧度化角度
度数×＝弧度数 弧度数×°＝度数
360°＝2π_rad 2π rad＝360°
180°＝π_rad π rad＝180°
1°＝ rad≈0.017 45 rad 1 rad＝°≈57.30°
(2)一些特殊角的度数与弧度的换算
度 0° 1° 30° 45° 60° 90° 120° 135° 150° 180° 270° 360°
弧度 0 π 2π
3．扇形的弧长与面积公式
　　　公式 度量制　　　 弧长公式 扇形面积公式
角度制 l＝ S＝
弧度制 l＝α·r (0<α<2π) S＝lr＝αr2 (0<α<2π)
[点睛]　(1)由扇形的弧长及面积公式可知，对于α，r，l，S可以“知二求二”．
(2)弧度制下的弧长公式和扇形面积公式有很多优越性，但要注意角必须化为弧度后再计算．
典型例题
类型一　角度与弧度的互化
例1　将下列角度与弧度进行互化．
(1)20°；(2)－15°；(3)；(4)－.
解　(1)20°＝＝.
(2)－15°＝－＝－.
(3)＝×180°＝105°.
(4)－＝－×180°＝－396°.
总结：　将角度转化为弧度时，要把带有分、秒的部分化为度之后，牢记π rad＝180°即可求解．把弧度转化为角度时，直接用弧度数乘以°即可．
类型二　用弧度制表示终边相同的角
例2　把下列各角化成2kπ＋α(0≤α<2π，k∈Z)的形式，并指出是第几象限角．
(1)－1 500°；(2)；(3)－4.
解　(1)∵－1 500°＝－1 800°＋300°＝－5×360°＋300°.
∴－1 500°可化成－10π＋，是第四象限角．
(2)∵＝2π＋，
∴与终边相同，是第四象限角．
(3)∵－4＝－2π＋(2π－4)，＜2π－4＜π.
∴－4与2π－4终边相同，是第二象限角．
总结：　用弧度制表示终边相同的角2kπ＋α(k∈Z)时，其中2kπ是π的偶数倍，而不是整数倍，还要注意角度制与弧度制不能混用．
跟踪训练　(1)把－1 480°写成α＋2kπ(k∈Z)的形式，其中0≤α≤2π；
(2)在[0°，720°]内找出与角终边相同的角．
解　(1)∵－1 480°＝－1 480×＝－，
而－＝－10π＋，且0≤α≤2π，∴α＝.
∴－1 480°＝＋2×(－5)π.
(2)∵＝×°＝72°，
∴终边与角相同的角为θ＝72°＋k·360°(k∈Z)，
当k＝0时，θ＝72°；当k＝1时，θ＝432°.
∴在[0°，720°]内与角终边相同的角为72°，432°.
类型三　扇形的弧长及面积公式的应用
例3　(1)若扇形的中心角为120°，半径为，则此扇形的面积为(　　)
A．π B. C. D.
(2)如果2弧度的圆心角所对的弦长为4，那么这个圆心角所对的弧长为(　　)
A．2 B. C．2sin 1 D.
答案　(1)A　(2)D
解析　(1)扇形的中心角为120°＝，半径为，
所以S扇形＝|α|r2＝××()2＝π.
(2)连接圆心与弦的中点，则以弦心距、弦长的一半、半径长为长度的线段构成一个直角三角形，半弦长为2，其所对的圆心角也为2，故半径长为.这个圆心角所对的弧长为2×＝.
总结：　联系半径、弧长和圆心角的有两个公式：一是S＝lr＝|α|r2，二是l＝|α|r，如果已知其中两个，就可以求出另一个．求解时应注意先把度化为弧度，再计算．
跟踪训练3　一个扇形的面积为1，周长为4，求圆心角的弧度数．
解　设扇形的半径为R，弧长为l，则2R＋l＝4，
∴l＝4－2R，根据扇形面积公式S＝lR，
得1＝(4－2R)·R，
∴R＝1，∴l＝2，∴α＝＝＝2，
即扇形的圆心角为2 rad.
由于弧度制是一个新的角单位制的概念,主要是让学生理解弧度制的意义,重点是让学生能正确进行弧度制与角度制的换算,并理解任意角的集合与实数集之间建立一一对应的关系,关键是让学生学会类比思想,并让学生学会在弧度制下的弧长公式,及扇形的面积公式。