北师大版七年级下册 4.3 探索三角形全等的条件课件(共15张PPT)
文档属性
| 名称 | 北师大版七年级下册 4.3 探索三角形全等的条件课件(共15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 276.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-18 11:30:21 | ||
图片预览





文档简介
(共16张PPT)
第2课时 角边角与角角边
北师大版 七年级下册
三角形包含几个元素?
想证明两个三角形全等,至少需要
几组元素分别对应相等?
情境导入
刘星把一块三角形的玻璃打碎成了两块,现在要去玻璃店配一块完全一样的玻璃,那么最省事的办法是带哪块去?为什么?
两角和它们的夹边分别对应相等的两个三角形全等,简写成“角边角”或“A.S.A”
判定方法
探索新知
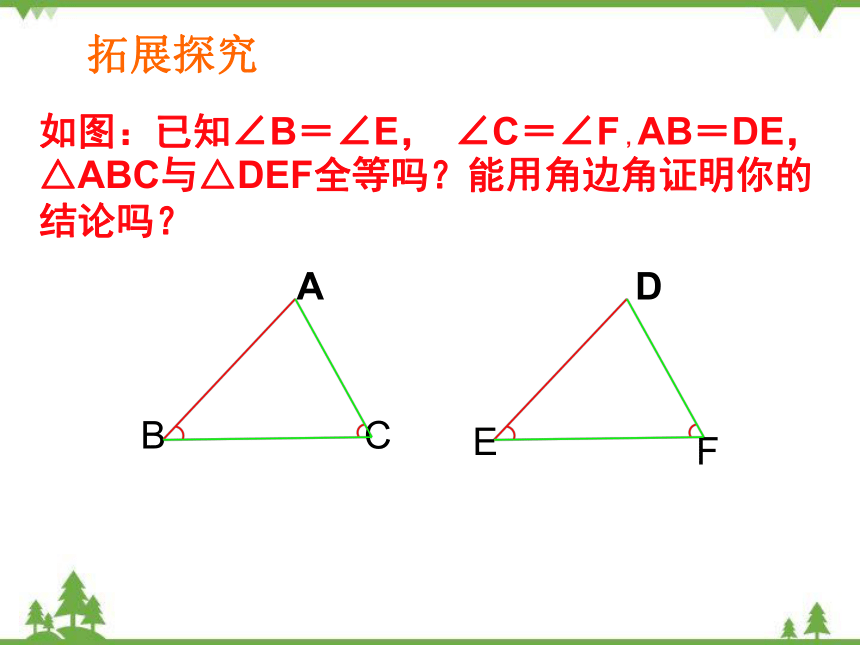
如图:已知∠B=∠E, ∠C=∠F , AB=DE, △ABC与△DEF全等吗?能用角边角证明你的结论吗?
A
B
C
D
E
F
拓展探究
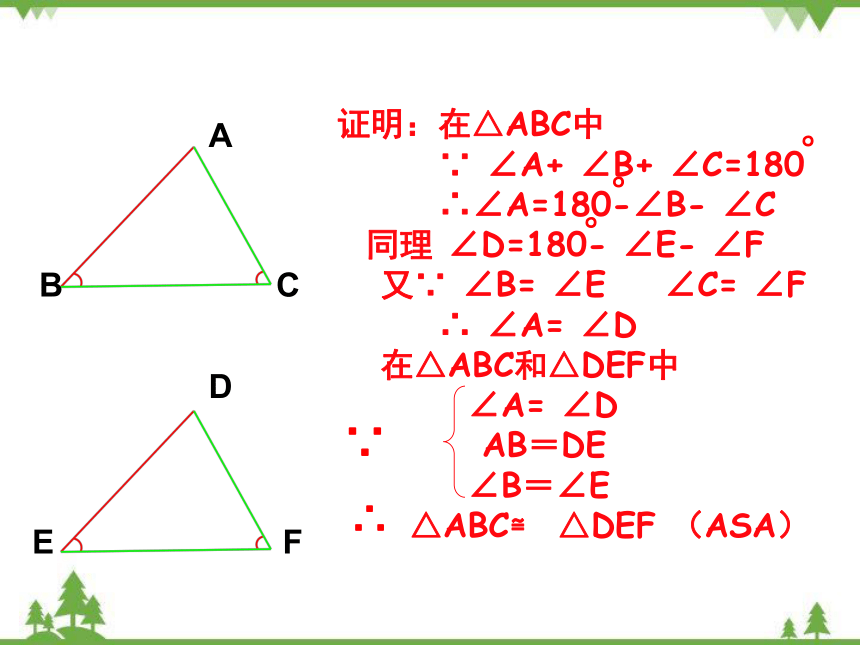
证明:在△ABC中
∵ ∠A+ ∠B+ ∠C=180
∴∠A=180-∠B- ∠C
同理 ∠D=180- ∠E- ∠F
又∵ ∠B= ∠E ∠C= ∠F
∴ ∠A= ∠D
在△ABC和△DEF中
∠A= ∠D
AB=DE
∠B=∠E
△ABC≌ △DEF (ASA)
∴
∵
°
°
°
A
B
C
E
D
F
两角和其中一角的对边分别对应相等的两个三角形全等,简写成“角角边”或“A.A.S.”
判定方法
两角和它们的夹边分别对应相等的两个三角形全等,简写成“角边角”或“A.S.A.”
两角和其中一角的对边分别对应相等的两个三角形全等,简写成“角角边”或“A.A.S.”
角边角
角角边
练一练:
如图∠ACB=∠DFE,BC=EF,根据A.S.A.或A.A.S.,那么应补充一个直接条件 --------------------------,才能使△ABC≌△DEF
A
B
C
D
E
F
∠B=∠E
⌒
⌒
或∠A=∠D
随堂演练
如图:已知AD = AE ,∠B=∠C,
△ABD与△ACE全等吗?为什么?
∴△ABD≌△ACE( A.A.S. )
A
D
E
C
B
⌒
⌒
如图要测量河两岸相对的两点A、B的距离,先在AB 的垂线BF上取两点C、D,使BC = DC,再定出BF的垂线DE,使E与A,C在一条直线上,这时测得DE的长就是AB的长。为什么?
B
A
●
●
D
C
E
F
能力提升
证明:在△ABC和△EDC中
∠ABC= ∠EDC=90 ° (已知)
BC=DC(已知)
∠ACB=∠ECD(对顶角)
△ABC和△EDC中(A.S.A.)
AB = ED
∵
∴
∴
⌒
⌒
通过这节课的学习活动,你有什么收获?
课堂小结
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
学习这件事不在乎有没有人教你,最重要的是在于你自己有没有觉悟和恒心。 —— 法布尔
第2课时 角边角与角角边
北师大版 七年级下册
三角形包含几个元素?
想证明两个三角形全等,至少需要
几组元素分别对应相等?
情境导入
刘星把一块三角形的玻璃打碎成了两块,现在要去玻璃店配一块完全一样的玻璃,那么最省事的办法是带哪块去?为什么?
两角和它们的夹边分别对应相等的两个三角形全等,简写成“角边角”或“A.S.A”
判定方法
探索新知
如图:已知∠B=∠E, ∠C=∠F , AB=DE, △ABC与△DEF全等吗?能用角边角证明你的结论吗?
A
B
C
D
E
F
拓展探究
证明:在△ABC中
∵ ∠A+ ∠B+ ∠C=180
∴∠A=180-∠B- ∠C
同理 ∠D=180- ∠E- ∠F
又∵ ∠B= ∠E ∠C= ∠F
∴ ∠A= ∠D
在△ABC和△DEF中
∠A= ∠D
AB=DE
∠B=∠E
△ABC≌ △DEF (ASA)
∴
∵
°
°
°
A
B
C
E
D
F
两角和其中一角的对边分别对应相等的两个三角形全等,简写成“角角边”或“A.A.S.”
判定方法
两角和它们的夹边分别对应相等的两个三角形全等,简写成“角边角”或“A.S.A.”
两角和其中一角的对边分别对应相等的两个三角形全等,简写成“角角边”或“A.A.S.”
角边角
角角边
练一练:
如图∠ACB=∠DFE,BC=EF,根据A.S.A.或A.A.S.,那么应补充一个直接条件 --------------------------,才能使△ABC≌△DEF
A
B
C
D
E
F
∠B=∠E
⌒
⌒
或∠A=∠D
随堂演练
如图:已知AD = AE ,∠B=∠C,
△ABD与△ACE全等吗?为什么?
∴△ABD≌△ACE( A.A.S. )
A
D
E
C
B
⌒
⌒
如图要测量河两岸相对的两点A、B的距离,先在AB 的垂线BF上取两点C、D,使BC = DC,再定出BF的垂线DE,使E与A,C在一条直线上,这时测得DE的长就是AB的长。为什么?
B
A
●
●
D
C
E
F
能力提升
证明:在△ABC和△EDC中
∠ABC= ∠EDC=90 ° (已知)
BC=DC(已知)
∠ACB=∠ECD(对顶角)
△ABC和△EDC中(A.S.A.)
AB = ED
∵
∴
∴
⌒
⌒
通过这节课的学习活动,你有什么收获?
课堂小结
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
学习这件事不在乎有没有人教你,最重要的是在于你自己有没有觉悟和恒心。 —— 法布尔
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
