北师大版数学七年级下册 2.3.1平行线的性质(平行线的性质)-课件 (共14张PPT)
文档属性
| 名称 | 北师大版数学七年级下册 2.3.1平行线的性质(平行线的性质)-课件 (共14张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 346.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-17 12:16:34 | ||
图片预览


文档简介
(共14张PPT)
第二章 平行线与相交线
2.3 平行线的性质
知识回顾
独学2分钟 对学1分钟
独学:2分钟
要求:
对学:1分钟
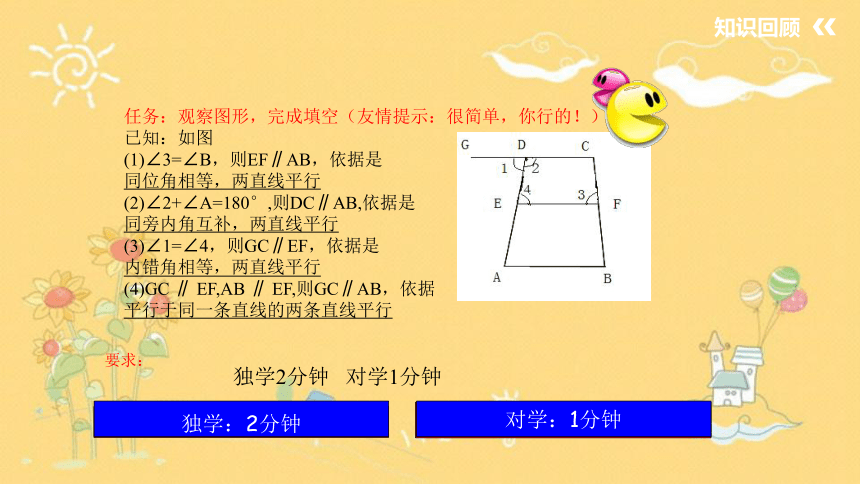
任务:观察图形,完成填空(友情提示:很简单,你行的!)
已知:如图
(1)∠3=∠B,则EF∥AB,依据是
同位角相等,两直线平行
(2)∠2+∠A=180°,则DC∥AB,依据是
同旁内角互补,两直线平行
(3)∠1=∠4,则GC∥EF,依据是
内错角相等,两直线平行
(4)GC ∥ EF,AB ∥ EF,则GC∥AB,依据
平行于同一条直线的两条直线平行
情景导入
根据同位角相等可以判定两直线平行,反过来如果两直线平行同位角之间有什么关系呢? 内错角,同旁内角之间又有什么关系呢?猜想一下?然后完成下面的探究:
(一)1探究1(独学两分钟,完成填空)
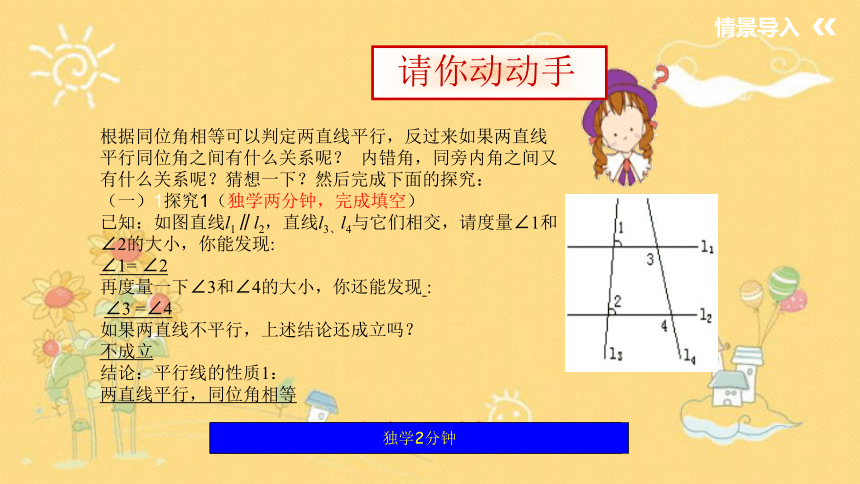
已知:如图直线l1∥l2,直线l3、l4与它们相交,请度量∠1和∠2的大小,你能发现:
∠1= ∠2
再度量一下∠3和∠4的大小,你还能发现 :
∠3 =∠4
如果两直线不平行,上述结论还成立吗?
不成立
结论:平行线的性质1:
两直线平行,同位角相等
独学2分钟
独学2分钟
请你动动手
情景导入
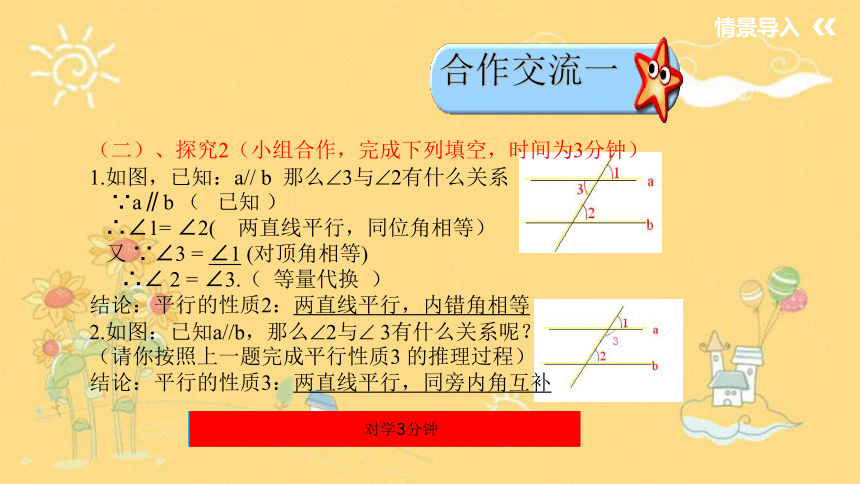
(二)、探究2(小组合作,完成下列填空,时间为3分钟)
1.如图,已知:a// b 那么 3与 2有什么关系
∵a∥b ( 已知 )
∴∠1= ∠2( 两直线平行,同位角相等)
又 ∵∠3 = ∠1 (对顶角相等)
∴∠ 2 = ∠3.( 等量代换 )
结论:平行的性质2:两直线平行,内错角相等
2.如图:已知a//b,那么 2与 3有什么关系呢?
(请你按照上一题完成平行性质3 的推理过程)
结论:平行的性质3:两直线平行,同旁内角互补
对学3分钟
合作交流一
对学对学3分钟
归纳整理
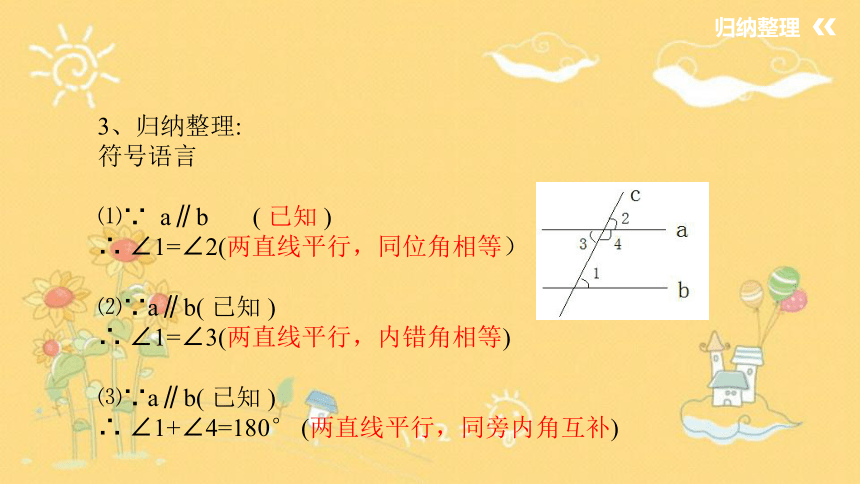
3、归纳整理:
符号语言
⑴∵ a∥b ( 已知 )
∴ ∠1=∠2(两直线平行,同位角相等)
⑵∵a∥b( 已知 )
∴ ∠1=∠3(两直线平行,内错角相等)
⑶∵a∥b( 已知 )
∴ ∠1+∠4=180° (两直线平行,同旁内角互补)
新知探索1
要求:
独学2分钟
对学1分钟
对学:1分钟
独学:2分钟
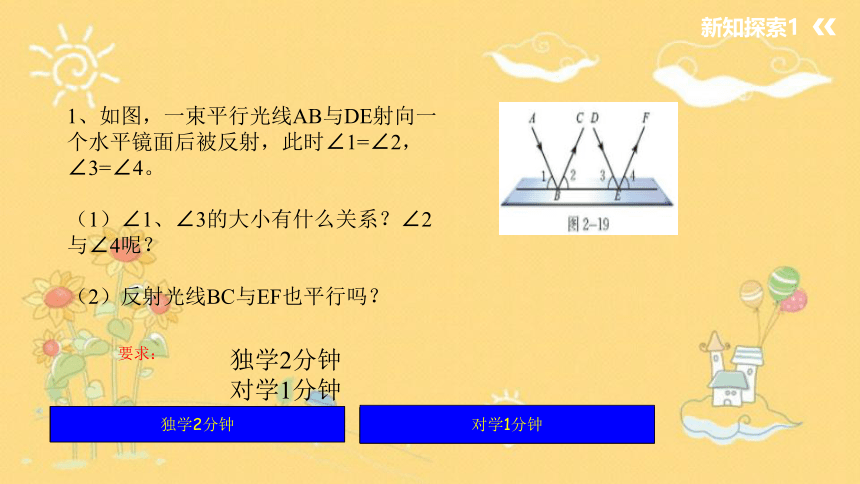
1、如图,一束平行光线AB与DE射向一个水平镜面后被反射,此时∠1=∠2,∠3=∠4。
(1)∠1、∠3的大小有什么关系?∠2与∠4呢?
(2)反射光线BC与EF也平行吗?
独学2分钟
对学1分钟
目标检测1
独学:1分钟
对学:1分钟
1、 如图,已知AD∥BE,AC∥DE, 可推出(1) ∠3= ∠4 (2)AB∥CD。填出推理理由。
证明 :(1)∵AD ∥BE( )
∴ ∠3= ∠5 ( )
又∵AC∥DE( )
∴ ∠5= ∠4 ( )
∴ ∠3= ∠4 ( )
(2)∵AD∥BE( )
∴ ∠1= ∠6 ( )
又∵ ∠1= ∠2 ( )
∴ ∠2= ∠6 ( )
∴AB∥CD ( )
#k#b#1#新#课#
目标检测1
2、如图,下列推理所注理由正确的是( )
A、∵DE∥BC ∴ ∠1= ∠C (同位角相等,两直线平行)
B、∵ ∠2= ∠3 ∴ DE∥BC(内错角相等,两直线平行)
C、∵DE∥BC ∴ ∠2= ∠3 (两直线平行,内错角相等)
D、∵ ∠1= ∠C ∴DE∥BC(两直线平行,同位角相等)
独学1分钟
独学1分钟
新知探索2
例:如图,AE∥CD,若∠1=37° , ∠D=54° ,求∠2和∠BAE的度数.
师生互动,典例示范
目标检测2
1、∠1和∠2是直线AB、CD被直线EF所截而成的内错角,那么∠1和∠2 的大小关系是( )
A.∠1=∠2 B.∠1>∠2; C.∠1<∠2 D.无法确定
2(2015山东临沂)如图,直线a//b,∠1=60°,∠2=40°,则∠3等于 ( )
A. 40° B. 60° C. 80° D. 100°
3、一辆汽车在笔直的公路上行驶,在两次转弯后,仍在原来的方向上平行前进,那么这两次转弯的角度可以是( )
A、先右转80o,再左转100 o B、先左转80 o ,再右转80 o
C、先左转80 o ,再左转100 o D、先右转80 o,再右转80
目标检测2
图4
4、(2015湖南省益阳市)如图4,直线AB∥CD,BC平分∠ABD, ∠1=65 ,求∠2的度数
独学5分钟
独学5分钟
目标检测2
D
C
E
F
G
G
1
2
小明在纸上画了一个角∠A,准备用量角器测量它的度数时,因不小心将纸片撕破,只剩下如图的一部分,如果不能延长DC、FE的话,你能帮他设计出多少种方法可以测出∠A的度数?
小结
两直线平行
同位角相等
内错角相等
同旁内角互补
线的关系
角的关系
判定
性质
平行线的性质和平行线的判定方法的 区 别 与 联 系
作业布置
1、完成数学作业本
2、完成一课一练的训练案
3、完成导学案课后学习
第二章 平行线与相交线
2.3 平行线的性质
知识回顾
独学2分钟 对学1分钟
独学:2分钟
要求:
对学:1分钟
任务:观察图形,完成填空(友情提示:很简单,你行的!)
已知:如图
(1)∠3=∠B,则EF∥AB,依据是
同位角相等,两直线平行
(2)∠2+∠A=180°,则DC∥AB,依据是
同旁内角互补,两直线平行
(3)∠1=∠4,则GC∥EF,依据是
内错角相等,两直线平行
(4)GC ∥ EF,AB ∥ EF,则GC∥AB,依据
平行于同一条直线的两条直线平行
情景导入
根据同位角相等可以判定两直线平行,反过来如果两直线平行同位角之间有什么关系呢? 内错角,同旁内角之间又有什么关系呢?猜想一下?然后完成下面的探究:
(一)1探究1(独学两分钟,完成填空)
已知:如图直线l1∥l2,直线l3、l4与它们相交,请度量∠1和∠2的大小,你能发现:
∠1= ∠2
再度量一下∠3和∠4的大小,你还能发现 :
∠3 =∠4
如果两直线不平行,上述结论还成立吗?
不成立
结论:平行线的性质1:
两直线平行,同位角相等
独学2分钟
独学2分钟
请你动动手
情景导入
(二)、探究2(小组合作,完成下列填空,时间为3分钟)
1.如图,已知:a// b 那么 3与 2有什么关系
∵a∥b ( 已知 )
∴∠1= ∠2( 两直线平行,同位角相等)
又 ∵∠3 = ∠1 (对顶角相等)
∴∠ 2 = ∠3.( 等量代换 )
结论:平行的性质2:两直线平行,内错角相等
2.如图:已知a//b,那么 2与 3有什么关系呢?
(请你按照上一题完成平行性质3 的推理过程)
结论:平行的性质3:两直线平行,同旁内角互补
对学3分钟
合作交流一
对学对学3分钟
归纳整理
3、归纳整理:
符号语言
⑴∵ a∥b ( 已知 )
∴ ∠1=∠2(两直线平行,同位角相等)
⑵∵a∥b( 已知 )
∴ ∠1=∠3(两直线平行,内错角相等)
⑶∵a∥b( 已知 )
∴ ∠1+∠4=180° (两直线平行,同旁内角互补)
新知探索1
要求:
独学2分钟
对学1分钟
对学:1分钟
独学:2分钟
1、如图,一束平行光线AB与DE射向一个水平镜面后被反射,此时∠1=∠2,∠3=∠4。
(1)∠1、∠3的大小有什么关系?∠2与∠4呢?
(2)反射光线BC与EF也平行吗?
独学2分钟
对学1分钟
目标检测1
独学:1分钟
对学:1分钟
1、 如图,已知AD∥BE,AC∥DE, 可推出(1) ∠3= ∠4 (2)AB∥CD。填出推理理由。
证明 :(1)∵AD ∥BE( )
∴ ∠3= ∠5 ( )
又∵AC∥DE( )
∴ ∠5= ∠4 ( )
∴ ∠3= ∠4 ( )
(2)∵AD∥BE( )
∴ ∠1= ∠6 ( )
又∵ ∠1= ∠2 ( )
∴ ∠2= ∠6 ( )
∴AB∥CD ( )
#k#b#1#新#课#
目标检测1
2、如图,下列推理所注理由正确的是( )
A、∵DE∥BC ∴ ∠1= ∠C (同位角相等,两直线平行)
B、∵ ∠2= ∠3 ∴ DE∥BC(内错角相等,两直线平行)
C、∵DE∥BC ∴ ∠2= ∠3 (两直线平行,内错角相等)
D、∵ ∠1= ∠C ∴DE∥BC(两直线平行,同位角相等)
独学1分钟
独学1分钟
新知探索2
例:如图,AE∥CD,若∠1=37° , ∠D=54° ,求∠2和∠BAE的度数.
师生互动,典例示范
目标检测2
1、∠1和∠2是直线AB、CD被直线EF所截而成的内错角,那么∠1和∠2 的大小关系是( )
A.∠1=∠2 B.∠1>∠2; C.∠1<∠2 D.无法确定
2(2015山东临沂)如图,直线a//b,∠1=60°,∠2=40°,则∠3等于 ( )
A. 40° B. 60° C. 80° D. 100°
3、一辆汽车在笔直的公路上行驶,在两次转弯后,仍在原来的方向上平行前进,那么这两次转弯的角度可以是( )
A、先右转80o,再左转100 o B、先左转80 o ,再右转80 o
C、先左转80 o ,再左转100 o D、先右转80 o,再右转80
目标检测2
图4
4、(2015湖南省益阳市)如图4,直线AB∥CD,BC平分∠ABD, ∠1=65 ,求∠2的度数
独学5分钟
独学5分钟
目标检测2
D
C
E
F
G
G
1
2
小明在纸上画了一个角∠A,准备用量角器测量它的度数时,因不小心将纸片撕破,只剩下如图的一部分,如果不能延长DC、FE的话,你能帮他设计出多少种方法可以测出∠A的度数?
小结
两直线平行
同位角相等
内错角相等
同旁内角互补
线的关系
角的关系
判定
性质
平行线的性质和平行线的判定方法的 区 别 与 联 系
作业布置
1、完成数学作业本
2、完成一课一练的训练案
3、完成导学案课后学习
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
