山东省德州市某中学2012-2013学年高二4月月考 数文
文档属性
| 名称 | 山东省德州市某中学2012-2013学年高二4月月考 数文 |  | |
| 格式 | zip | ||
| 文件大小 | 104.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-08 20:41:12 | ||
图片预览


文档简介
高二月考数学文科试题
第I卷(满分60分)(时间120分钟,总分150分)
选择题(本题共12小题,每题5分,共60分)
1、若事件A与B相互独立,则下列不相互独立的是 ( )
A. A与 B. C. D.
2.化简( )
A. B. C. D.
3.用反证法证明:“若a,b两数之积为0,则a,b至少有一个为0”,应假设( ).
A.a,b没有一个为0 B.a,b只有一个为0
C.a,b至多有一个为0 D.a,b两个都为0
4.如果女大学生身高x(cm)与体重y(kg)的关系满足线性回归模型y=0.85x-88+e,
其中|e|≤4,如果已知某女大学生身高160 cm,则体重预计不会低于( ).
A.44 kg B.46 kg C.50 kg D.54 kg
5.“函数在一点的导数值为0”是“函数在这点取极值”的( )
A、充分不必要条件 B、必要不充分条件
C、充要条件 D、既不充分也不必要条件
6. 有一段演绎推理是这样的:“直线平行于平面,则平行于平面内所有直线;已知直线平面,直线平面,直线∥平面,则直线∥直线”的结论显然是错误的,这是因为
A.大前提错误 B.小前提错误 C.推理形式错误 D.非以上错误
7.函数的导数是 ( )
A.??? B. C.?????? D.
8. 曲线3x2-y+6=0在x=-处的切线的倾斜角是
A. B.- C.π D.-π
9、满足条件的复数在复平面上对应点的轨迹是 ( )
A. 一条直线 B. 两条直线 C. 圆 D. 椭圆
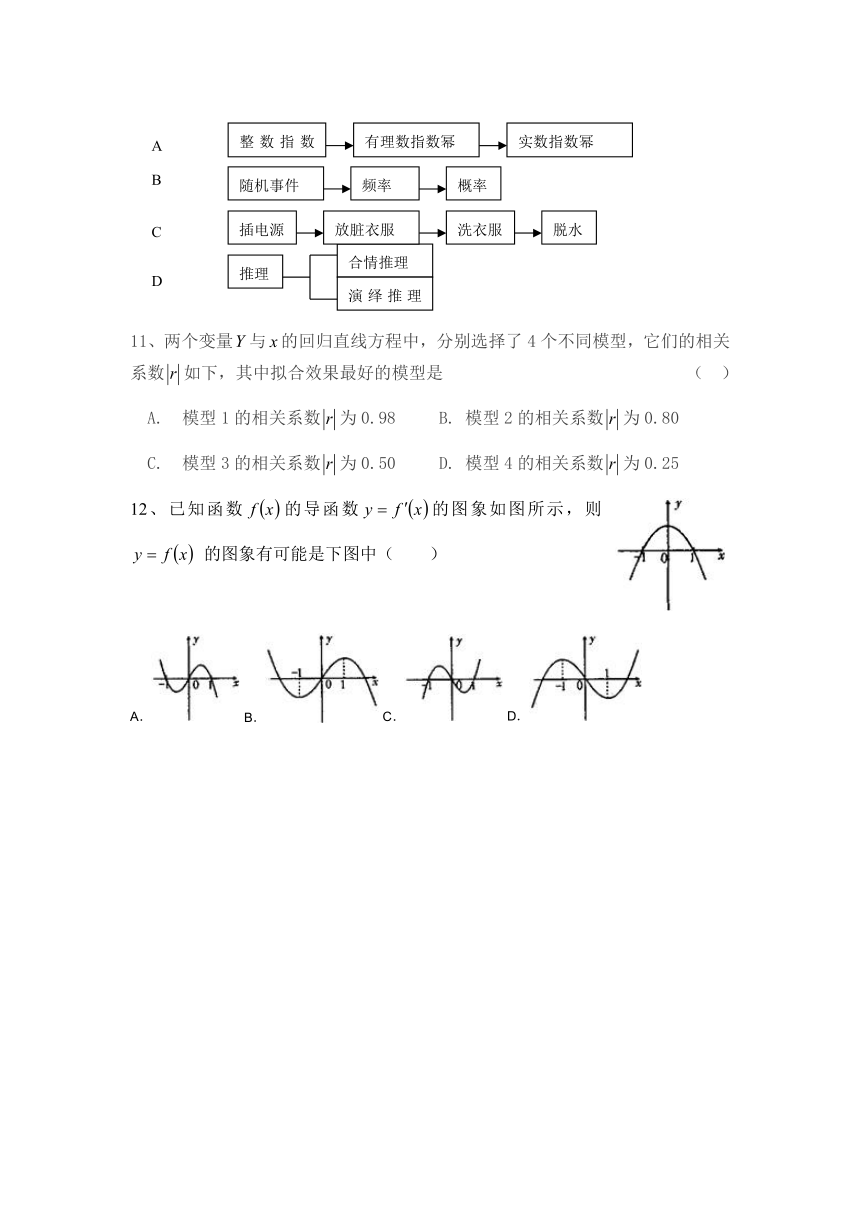
10 下列框图中,属于工序流程图的是
11、两个变量与的回归直线方程中,分别选择了4个不同模型,它们的相关系数如下,其中拟合效果最好的模型是 ( )
A. 模型1的相关系数为0.98 B. 模型2的相关系数为0.80
C. 模型3的相关系数为0.50 D. 模型4的相关系数为0.25
12、已知函数的导函数的图象如图所示,则 的图象有可能是下图中( )
A.
B.
C.
D.
第II卷(满分90分)
二、填空题(本题共4个小题.每小题4分,共16分)
13、如右图所示的程序输出的结果是 _________
14、已知复数与都是纯虚数,则=____________.
15.曲线在点处的切线方程是_____________
16.下面给出了关于复数的三种类比推理:
①复数的乘法运算法则可以类比多项式的乘法运算法则;
②由向量的性质可以类比复数的性质;
③由向量加法的几何意义可以类比得到复数加法的几何意义.
其中类比错误的是____________.
三、解答题(本题共6个小题,前5题每题12分,第6题14分,共74分,解答题应有必要的文字说明和步骤)
17、(本题满分12分)
已知复数,求.
18、(本题满分12分)设f(x)=x3+ 求函数f(x)的单调区间及其极值;
19、(本题满分12分)
在对人们休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人,女性中有43人重要的休闲方式是看电视,另外27人的休闲方式重要是运动;男性中有21人重要休闲方式是看电视,另外33人的重要休闲方式是运动。
(1)根据以上数据建立一个2×2列联表
(2)试问休闲方式和性别是否有关()
20、(本题满分12分)
设为坐标原点,已知向量分别对应复数且,(其中),若可以与任意实数比较大小,求的值.
21、(本题满分12分)
某工厂生产某种产品,已知该产品的月产量(吨)与每吨产品的销售价格(元/吨)之间的关系式为且生产吨的成本为元.问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入-成本)
22、(本题满分14分)
已知函数
⑴设,求函数的极值; ⑵在⑴的条件下,若函数 (其中为的导数)
在区间(1,3)上不是单调函数,求实数m的取值范围.
高二月考数学文科试题答案
选择题
C 2. A 3. A 4. A 5. D 6A 7. B 8. C 9. C 10. C 11.A 12.B
填空题
13. 1023 14. 15. 16. ②
三、解答题
17、解: ……(5分)
…… (12分)
18、解:(1)
解得 …………(4分)
+
0
-
-
0
+
↗
极大值
↙
↙
极小值
↗
…………(8分)
和
单调减区间为和 …………….(10分)
极大值为,极小值为……………(12分)
19解:(1)列联表如下:--------------------------------------------------4分
看电视
运动
合计
女性
43
27
70
男性
21
33
54
合计
64
60
124
(2) 提出假设:“休闲方式与性别无关”,------------------6分
由公式算得k=≈6.201,----------------9分
即我们有95%的把握认为“休闲方式与性别有关”.------------------------------12分
20、解:可以与任意实数比较大小, ……(2分)
= …… (8分)
解得 ……(10分)
…… (12分
21、解:由题意知
利润
…… (3分)
…… (5分)
解 …… (7分)
…… (9分)
是定义域内的唯一极值点
是函数的最大值点,此时 …… (11分)
答:当每月生产200吨时利润有最大值,最大值为3150000元. …… (12分)
22、解:(1) …… (2分)
……(3分)
解,得 …… (4分)
-
0
+
↙
极小值
↗
…… (6分)
由表可知,,无极大值 …… (7分)
(2)由(1)知
…… (8分)
…… (9分)
在区间(1,3)上不是单调函数,所以在区间(1,3)内有极值点……(10分)
满足 …… (12分)
即 解得 …… (14分)
第I卷(满分60分)(时间120分钟,总分150分)
选择题(本题共12小题,每题5分,共60分)
1、若事件A与B相互独立,则下列不相互独立的是 ( )
A. A与 B. C. D.
2.化简( )
A. B. C. D.
3.用反证法证明:“若a,b两数之积为0,则a,b至少有一个为0”,应假设( ).
A.a,b没有一个为0 B.a,b只有一个为0
C.a,b至多有一个为0 D.a,b两个都为0
4.如果女大学生身高x(cm)与体重y(kg)的关系满足线性回归模型y=0.85x-88+e,
其中|e|≤4,如果已知某女大学生身高160 cm,则体重预计不会低于( ).
A.44 kg B.46 kg C.50 kg D.54 kg
5.“函数在一点的导数值为0”是“函数在这点取极值”的( )
A、充分不必要条件 B、必要不充分条件
C、充要条件 D、既不充分也不必要条件
6. 有一段演绎推理是这样的:“直线平行于平面,则平行于平面内所有直线;已知直线平面,直线平面,直线∥平面,则直线∥直线”的结论显然是错误的,这是因为
A.大前提错误 B.小前提错误 C.推理形式错误 D.非以上错误
7.函数的导数是 ( )
A.??? B. C.?????? D.
8. 曲线3x2-y+6=0在x=-处的切线的倾斜角是
A. B.- C.π D.-π
9、满足条件的复数在复平面上对应点的轨迹是 ( )
A. 一条直线 B. 两条直线 C. 圆 D. 椭圆
10 下列框图中,属于工序流程图的是
11、两个变量与的回归直线方程中,分别选择了4个不同模型,它们的相关系数如下,其中拟合效果最好的模型是 ( )
A. 模型1的相关系数为0.98 B. 模型2的相关系数为0.80
C. 模型3的相关系数为0.50 D. 模型4的相关系数为0.25
12、已知函数的导函数的图象如图所示,则 的图象有可能是下图中( )
A.
B.
C.
D.
第II卷(满分90分)
二、填空题(本题共4个小题.每小题4分,共16分)
13、如右图所示的程序输出的结果是 _________
14、已知复数与都是纯虚数,则=____________.
15.曲线在点处的切线方程是_____________
16.下面给出了关于复数的三种类比推理:
①复数的乘法运算法则可以类比多项式的乘法运算法则;
②由向量的性质可以类比复数的性质;
③由向量加法的几何意义可以类比得到复数加法的几何意义.
其中类比错误的是____________.
三、解答题(本题共6个小题,前5题每题12分,第6题14分,共74分,解答题应有必要的文字说明和步骤)
17、(本题满分12分)
已知复数,求.
18、(本题满分12分)设f(x)=x3+ 求函数f(x)的单调区间及其极值;
19、(本题满分12分)
在对人们休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人,女性中有43人重要的休闲方式是看电视,另外27人的休闲方式重要是运动;男性中有21人重要休闲方式是看电视,另外33人的重要休闲方式是运动。
(1)根据以上数据建立一个2×2列联表
(2)试问休闲方式和性别是否有关()
20、(本题满分12分)
设为坐标原点,已知向量分别对应复数且,(其中),若可以与任意实数比较大小,求的值.
21、(本题满分12分)
某工厂生产某种产品,已知该产品的月产量(吨)与每吨产品的销售价格(元/吨)之间的关系式为且生产吨的成本为元.问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入-成本)
22、(本题满分14分)
已知函数
⑴设,求函数的极值; ⑵在⑴的条件下,若函数 (其中为的导数)
在区间(1,3)上不是单调函数,求实数m的取值范围.
高二月考数学文科试题答案
选择题
C 2. A 3. A 4. A 5. D 6A 7. B 8. C 9. C 10. C 11.A 12.B
填空题
13. 1023 14. 15. 16. ②
三、解答题
17、解: ……(5分)
…… (12分)
18、解:(1)
解得 …………(4分)
+
0
-
-
0
+
↗
极大值
↙
↙
极小值
↗
…………(8分)
和
单调减区间为和 …………….(10分)
极大值为,极小值为……………(12分)
19解:(1)列联表如下:--------------------------------------------------4分
看电视
运动
合计
女性
43
27
70
男性
21
33
54
合计
64
60
124
(2) 提出假设:“休闲方式与性别无关”,------------------6分
由公式算得k=≈6.201,----------------9分
即我们有95%的把握认为“休闲方式与性别有关”.------------------------------12分
20、解:可以与任意实数比较大小, ……(2分)
= …… (8分)
解得 ……(10分)
…… (12分
21、解:由题意知
利润
…… (3分)
…… (5分)
解 …… (7分)
…… (9分)
是定义域内的唯一极值点
是函数的最大值点,此时 …… (11分)
答:当每月生产200吨时利润有最大值,最大值为3150000元. …… (12分)
22、解:(1) …… (2分)
……(3分)
解,得 …… (4分)
-
0
+
↙
极小值
↗
…… (6分)
由表可知,,无极大值 …… (7分)
(2)由(1)知
…… (8分)
…… (9分)
在区间(1,3)上不是单调函数,所以在区间(1,3)内有极值点……(10分)
满足 …… (12分)
即 解得 …… (14分)
同课章节目录
