山东省德州市某中学2012-2013学年高二4月月考 数理
文档属性
| 名称 | 山东省德州市某中学2012-2013学年高二4月月考 数理 |  | |
| 格式 | zip | ||
| 文件大小 | 164.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-08 20:41:12 | ||
图片预览

文档简介
高二月考数学(理科)试题
第I卷
选择题(每小题5分,共60分)
1.已知向量的夹角为 ( )
A.0° B.45° C.90° D.180°
2.已知向量a=(1,1,0),b=(-1,0,2),且a+b与2 a-b互相垂直,则的值是( )
A. 1 B. C. D.
3.曲线在点处的切线方程为( ).
A. B. C. D.
4.已知 ( )
A. B.5,2 C. D.-5,-2
5.函数的定义域为开区间,导函数
在内的图象如图所示,
则函数在开区间内有极小值点
( )
A. 1个 B.2个 C.3个 D. 4个
6.已知A、B、C三点不共线,对平面ABC外的任一点O,下列条件中能确定点M与点A、B、C一定共面的是 ( )
A. B.
C. D.
7.由抛物线与直线所围成的图形的面积是( ).
A. B. C. D.
8. 已知函数在处可导,则等于 ( )
A. B.2 C.-2 D.0
9.函数,则导数=( )
A. B.
C. D.
10.已知对任意实数,有,且时,,则时( )
A. B.
C. D.
11.在棱长为1的正方体ABCD—A1B1C1D1中,M和N分别为A1B1和BB1的中点,那么直线AM与CN所成角的余弦值是 ( )
A. B. C. D.
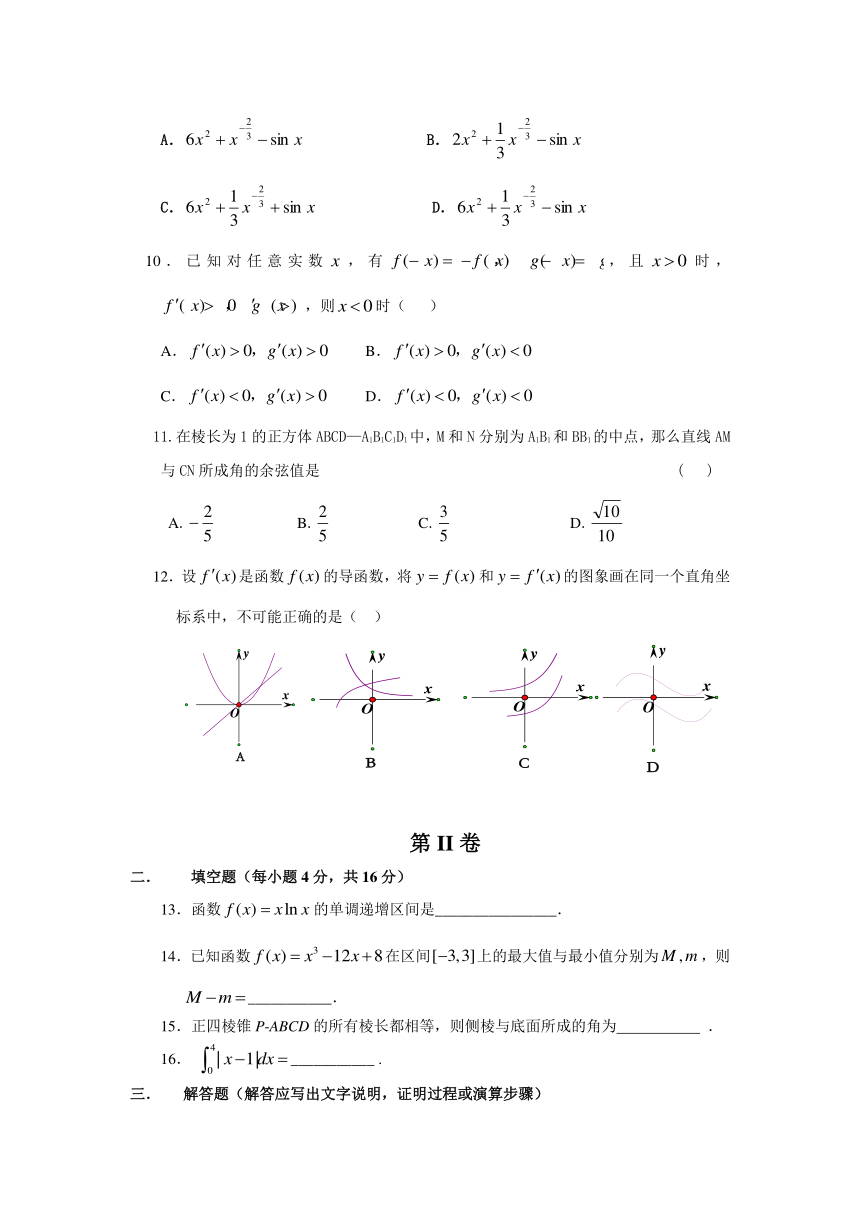
12.设是函数的导函数,将和的图象画在同一个直角坐标系中,不可能正确的是( )
第II卷
填空题(每小题4分,共16分)
13.函数的单调递增区间是________________.
14.已知函数在区间上的最大值与最小值分别为,则___________.
15.正四棱锥P-ABCD的所有棱长都相等,则侧棱与底面所成的角为 .
16. ___________ .
三. 解答题(解答应写出文字说明,证明过程或演算步骤)
17.(本小题12分)
已知,求的值.
18.(本小题12分)
已知函数在处取得极值.
(1)讨论和是函数的极大值还是极小值;
(2)过点作曲线的切线,求此切线方程.
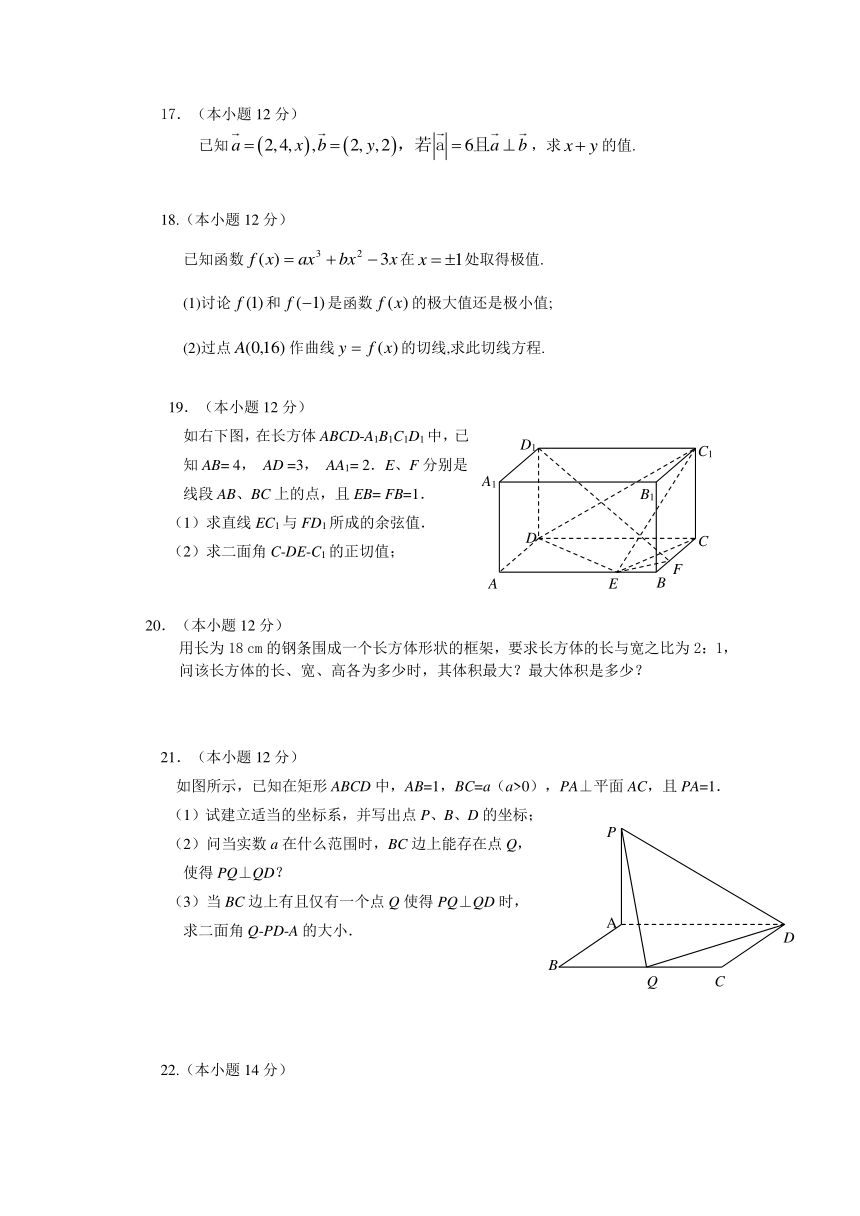
19.(本小题12分)
如右下图,在长方体ABCD-A1B1C1D1中,已知AB= 4, AD =3, AA1= 2.E、F分别是线段AB、BC上的点,且EB= FB=1.
(1)求直线EC1与FD1所成的余弦值.
(2)求二面角C-DE-C1的正切值;
20.(本小题12分)
用长为18 cm的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2:1,问该长方体的长、宽、高各为多少时,其体积最大?最大体积是多少?
21.(本小题12分)
如图所示,已知在矩形ABCD中,AB=1,BC=a(a>0),PA⊥平面AC,且PA=1.
(1)试建立适当的坐标系,并写出点P、B、D的坐标;
(2)问当实数a在什么范围时,BC边上能存在点Q,
使得PQ⊥QD?
(3)当BC边上有且仅有一个点Q使得PQ⊥QD时,
求二面角Q-PD-A的大小.
22.(本小题14分)
已知
(1)当时,求函数的单调区间。
(2)当时,讨论函数的单调增区间。
(3)是否存在负实数,使,函数有最小值-3?
高二月考数学(理科)答案
一.选择题 CDBAA DAADB BD
二.填空 13. 14. 32 15. 16. 5
17.解:由………………………………3分
又即
………………………………………………6分
由①②有: ………………10分
…………………………………………12分
18.解:(1),依题意,
,即 解得 ┅┅ (3分)
∴,∴
令,得
若,则
故在上是增函数;
若,则
故在上是减函数;
所以是极大值,是极小值。 ┅┅┅┅┅┅┅┅ (6分)
(2)曲线方程为,点不在曲线上。
设切点为,则
由知,切线方程为
┅┅┅┅┅┅┅┅┅┅ (9分)
又点在切线上,有
化简得 ,解得
所以切点为,切线方程为 ┅┅┅┅┅┅ (12分)
19.(1)如图,以A为原点,分别为x轴,y轴,z轴的正向建立空间直角坐标系 A-xyz,则有D(0,3,0)、D1(0,3,2)、E(3,0,0)、F(4,1,0)、C1(4, 3,2).
于是,,
. 设EC1与FD1所成角为(,则
. ………4分
(2)设向量与平面C1DE垂直,则有
.
∴其中z>0.
取n0=(-1,-1,2),则n0是一个与平面C1DE垂直的向量.
∵向量=(0,0,2)与平面CDE垂直,
∴n0与所成的角θ为二面角C-DE-C1的平面角.
∵, ………………10分
∴. ………………………………………………12分
20.解:设长方体的宽为x(m),则长为2x(m),
则高为. ………2分
故长方体的体积为
………………4分
从而
令V′(x)=0,解得x=0(舍去)或x=1,因此x=1. ……………8分
当0<x<1时,V′(x)>0;当1<x<时,V′(x)<0,
故在x=1处V(x)取得极大值,并且这个极大值就是V(x)的最大值。 ………10分
从而最大体积V=9×12-6×13(m3),此时长方体的长为2 m,高为1.5 m. ┅11分
答:当长方体的长为2 m时,宽为1 m,高为1.5 m时,体积最大,最大体积为3 m3。 12分
21.(1)以A为坐标原点,AB、AD、AP分
别为x、y、z轴建立坐标系如图所示.
∵PA=AB=1,BC=a,
∴P(0,0,1),B(1,1,0),
D(0,a,0). …………2分
(2)设点Q(1,x,0),则
.
由,得x2-ax+1=0.
显然当该方程有实数解时,BC边上才存在点Q,使得PQ⊥QD,故⊿=a2-4≥0.
因a>0,故a的取值范围为a≥0. ……………6分
(3)易见,当a=2时,BC上仅有一点满足题意,此时x=1,即Q为BC的中点.
取AD的中点M,过M作MN⊥PD,垂足为N,连结QM、QN.则M(0,1,0),P(0,0,1),D(0,2,0).
∵D、N、P三点共线,
∴.
又,且,
故.
于是.
故.
∵,
∴.
∴∠MNQ为所求二面角的平面角.
∵,
∴所求二面角为. …………………………12分
22.(1)当a=1时,
或递减; 递增; ……3分
(2)
①当递增;
②当递增;
③当或递增;
④当递增;
⑤当或递增; …………8分
(3)因由②分两类(依据:单调性,极小值点是否在区间[-1,0]上是分类“契机”:
①当 递增,,解得
②当由单调性知:,化简得:,解得
不合要求;
综上,为所求。 ………………………………14分
第I卷
选择题(每小题5分,共60分)
1.已知向量的夹角为 ( )
A.0° B.45° C.90° D.180°
2.已知向量a=(1,1,0),b=(-1,0,2),且a+b与2 a-b互相垂直,则的值是( )
A. 1 B. C. D.
3.曲线在点处的切线方程为( ).
A. B. C. D.
4.已知 ( )
A. B.5,2 C. D.-5,-2
5.函数的定义域为开区间,导函数
在内的图象如图所示,
则函数在开区间内有极小值点
( )
A. 1个 B.2个 C.3个 D. 4个
6.已知A、B、C三点不共线,对平面ABC外的任一点O,下列条件中能确定点M与点A、B、C一定共面的是 ( )
A. B.
C. D.
7.由抛物线与直线所围成的图形的面积是( ).
A. B. C. D.
8. 已知函数在处可导,则等于 ( )
A. B.2 C.-2 D.0
9.函数,则导数=( )
A. B.
C. D.
10.已知对任意实数,有,且时,,则时( )
A. B.
C. D.
11.在棱长为1的正方体ABCD—A1B1C1D1中,M和N分别为A1B1和BB1的中点,那么直线AM与CN所成角的余弦值是 ( )
A. B. C. D.
12.设是函数的导函数,将和的图象画在同一个直角坐标系中,不可能正确的是( )
第II卷
填空题(每小题4分,共16分)
13.函数的单调递增区间是________________.
14.已知函数在区间上的最大值与最小值分别为,则___________.
15.正四棱锥P-ABCD的所有棱长都相等,则侧棱与底面所成的角为 .
16. ___________ .
三. 解答题(解答应写出文字说明,证明过程或演算步骤)
17.(本小题12分)
已知,求的值.
18.(本小题12分)
已知函数在处取得极值.
(1)讨论和是函数的极大值还是极小值;
(2)过点作曲线的切线,求此切线方程.
19.(本小题12分)
如右下图,在长方体ABCD-A1B1C1D1中,已知AB= 4, AD =3, AA1= 2.E、F分别是线段AB、BC上的点,且EB= FB=1.
(1)求直线EC1与FD1所成的余弦值.
(2)求二面角C-DE-C1的正切值;
20.(本小题12分)
用长为18 cm的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2:1,问该长方体的长、宽、高各为多少时,其体积最大?最大体积是多少?
21.(本小题12分)
如图所示,已知在矩形ABCD中,AB=1,BC=a(a>0),PA⊥平面AC,且PA=1.
(1)试建立适当的坐标系,并写出点P、B、D的坐标;
(2)问当实数a在什么范围时,BC边上能存在点Q,
使得PQ⊥QD?
(3)当BC边上有且仅有一个点Q使得PQ⊥QD时,
求二面角Q-PD-A的大小.
22.(本小题14分)
已知
(1)当时,求函数的单调区间。
(2)当时,讨论函数的单调增区间。
(3)是否存在负实数,使,函数有最小值-3?
高二月考数学(理科)答案
一.选择题 CDBAA DAADB BD
二.填空 13. 14. 32 15. 16. 5
17.解:由………………………………3分
又即
………………………………………………6分
由①②有: ………………10分
…………………………………………12分
18.解:(1),依题意,
,即 解得 ┅┅ (3分)
∴,∴
令,得
若,则
故在上是增函数;
若,则
故在上是减函数;
所以是极大值,是极小值。 ┅┅┅┅┅┅┅┅ (6分)
(2)曲线方程为,点不在曲线上。
设切点为,则
由知,切线方程为
┅┅┅┅┅┅┅┅┅┅ (9分)
又点在切线上,有
化简得 ,解得
所以切点为,切线方程为 ┅┅┅┅┅┅ (12分)
19.(1)如图,以A为原点,分别为x轴,y轴,z轴的正向建立空间直角坐标系 A-xyz,则有D(0,3,0)、D1(0,3,2)、E(3,0,0)、F(4,1,0)、C1(4, 3,2).
于是,,
. 设EC1与FD1所成角为(,则
. ………4分
(2)设向量与平面C1DE垂直,则有
.
∴其中z>0.
取n0=(-1,-1,2),则n0是一个与平面C1DE垂直的向量.
∵向量=(0,0,2)与平面CDE垂直,
∴n0与所成的角θ为二面角C-DE-C1的平面角.
∵, ………………10分
∴. ………………………………………………12分
20.解:设长方体的宽为x(m),则长为2x(m),
则高为. ………2分
故长方体的体积为
………………4分
从而
令V′(x)=0,解得x=0(舍去)或x=1,因此x=1. ……………8分
当0<x<1时,V′(x)>0;当1<x<时,V′(x)<0,
故在x=1处V(x)取得极大值,并且这个极大值就是V(x)的最大值。 ………10分
从而最大体积V=9×12-6×13(m3),此时长方体的长为2 m,高为1.5 m. ┅11分
答:当长方体的长为2 m时,宽为1 m,高为1.5 m时,体积最大,最大体积为3 m3。 12分
21.(1)以A为坐标原点,AB、AD、AP分
别为x、y、z轴建立坐标系如图所示.
∵PA=AB=1,BC=a,
∴P(0,0,1),B(1,1,0),
D(0,a,0). …………2分
(2)设点Q(1,x,0),则
.
由,得x2-ax+1=0.
显然当该方程有实数解时,BC边上才存在点Q,使得PQ⊥QD,故⊿=a2-4≥0.
因a>0,故a的取值范围为a≥0. ……………6分
(3)易见,当a=2时,BC上仅有一点满足题意,此时x=1,即Q为BC的中点.
取AD的中点M,过M作MN⊥PD,垂足为N,连结QM、QN.则M(0,1,0),P(0,0,1),D(0,2,0).
∵D、N、P三点共线,
∴.
又,且,
故.
于是.
故.
∵,
∴.
∴∠MNQ为所求二面角的平面角.
∵,
∴所求二面角为. …………………………12分
22.(1)当a=1时,
或递减; 递增; ……3分
(2)
①当递增;
②当递增;
③当或递增;
④当递增;
⑤当或递增; …………8分
(3)因由②分两类(依据:单调性,极小值点是否在区间[-1,0]上是分类“契机”:
①当 递增,,解得
②当由单调性知:,化简得:,解得
不合要求;
综上,为所求。 ………………………………14分
同课章节目录
