人教版六年级下学期数学6.1.4比和比例课件(共21张PPT)
文档属性
| 名称 | 人教版六年级下学期数学6.1.4比和比例课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-17 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
比和比例
比
比例
意义:两个数相除也叫做两个数的比。
如:5÷4=5∶4
性质:比的前项与后项同时乘或除以相同的数,比值不变。
意义:表示两个比相等的式子叫做比例。
如:6∶12=1∶2
性质:在比例里,两内项之积等于两外项之积。
0.6 ∶ 0.4
前项 后项
比
意义
各部分名称
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
基本性质
两个数的比表示两个数相除。
新课讲解
1.关于比和比例的知识,你知道什么?它们有什么区别和联系?
比
意义 两个数相除又叫做这两个数的比。比表示两个数相除。
各部分名称 比由两项组成,比号前面的数叫做比的前项,比号后面的数叫做比的后项。
基本 性质 比的前项和后项同时乘或除以相同的数(0除外),比值不变。利用比的基本性质可以化简比。
化简比并求比值。
2.8 :3.5
朵朵
选一选。(将正确答案的序号填在括号里)[★★★]
(1)两个正方体的棱长比是2∶3,它的表面积之比是( )。
A.2∶3 B.4∶9 C.8∶27 D.4∶27
正方体的表面积=棱长×棱长×6
正方体表面积之比是棱长平方之比
表面积之比是(2×2):(3×3)
B
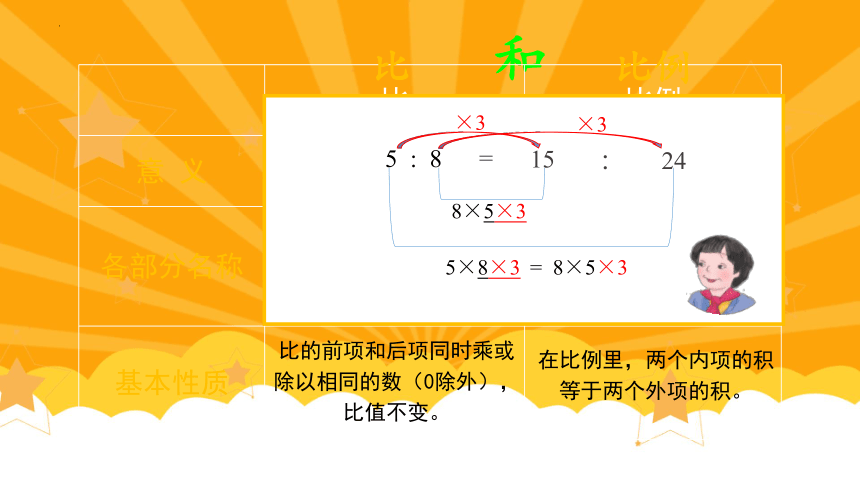
和
比 比例
意 义
各部分名称
基本性质
两个数的比表示两个数相 。
表示两个 相等的式子叫做比例。
0.6 ∶ 0.4
前项 后项
外项
内项
3: 2
0.6 : 0.4
=
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
在比例里,两个内项的积等于两个外项的积。
比
比例
除
比
5 : 8
5×8×3
8×5×3
= 8×5×3
×3
×3
15
: 24
=
新课讲解
你怎样判断两种相关联的量是成正比例关系还是成反比例关系?
正比例:两种相关联的量,其中一种量增加,另一种量也随着增加,一种量减少,另一种量也随着减少;两种量的比值一定。
反比例:两种相关联的量,其中一种量增加,另一种量反而减少,一种量减少,另一种量反而增加;两种量的积一定。
反比例:
xy=k(一定)
y
x
正比例:
=k(一定)
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做( )。它们的关系叫做( )。
如果用x和y表示两种相关联的量,用k表示它们的积,反比例关系可以用下面的式子表示:( )。
反比例
反比例关系
xy=k(一定)
把下面的比化成最简整数比,并求比值。[★★★]
∶ 0.25∶1.5 ∶ kg∶125 g
=2∶3
=1∶6
=11∶8
=8∶5
正、反比例的意义分别是什么?
正比例:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定。
反比例:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定。
课堂练习
植树节前夕,六年级同学来到山坡植树,原计划每人植树14棵,需要25人。实际每人植树10棵,还要增加多少人?
解:设还要增加x人。
14×25=10×(25+x)
x=10
答:还要增加10人。
A
两个数相除又叫做两个数的比。比的前项和后项同时乘(或除)相同的数(0除外)比值不变,这叫做基本性质。
B
表示两个比相等的式子叫作比例。在比例里,两个内项的积等于两个外项的积,这叫做比例的基本性质。
比和比例
C
正比例:
反比例:
x×y=k(一定)
水果超市原有苹果与梨的质量比是8∶3,苹果卖了 ,梨卖了50 kg后,苹果比梨多220 kg。水果超市原有苹果和梨共多少千克?[★★★★]
6.4-3
(220-50)÷( )
=50(kg)
50×(8+3)=550(kg)
答:水果超市原有苹果和梨共550kg。
水是由氢和氧按1 : 8 的质量比化合而成的。5.4 kg 的水含氢和氧各多少?
(教材第85页第3题)
判断每张表中的两种量是成正比例、反比例,还是不成比例,并说明理由。
成正比例, 因为比的前项和后项的比值一定。
成正比例, 因为小麦的质量和磨面粉质量的比值一定。
成反比例, 因为三角形的底和高的乘积一定。
不成比例,园的半径和面积的比值不一定。
总页数不变,即每天读的页数与天数的乘积一定
(教材第64页第8题)
小林读一本文学名著,如果每天读30页,8天可以读完,小林想6天读完,那么平均每天要读多少页?
每天读页数×天数 = 总页数(一定)
解:设平均每天要读x页。
6x=30×8
6x=240
x =40
答:平均每天要读40页。
解:设甲、乙两地之间的实际距离为x厘米。
1:25000 = 15:x
x = 15×25000
x = 375000
在比例尺是1:25000的地图上量得甲、乙两地之间的距离是15厘米,如果把它改画在比例尺为1:20000的地图上,甲、乙两地的图上距离应画多长?
同学们再见
比和比例
比
比例
意义:两个数相除也叫做两个数的比。
如:5÷4=5∶4
性质:比的前项与后项同时乘或除以相同的数,比值不变。
意义:表示两个比相等的式子叫做比例。
如:6∶12=1∶2
性质:在比例里,两内项之积等于两外项之积。
0.6 ∶ 0.4
前项 后项
比
意义
各部分名称
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
基本性质
两个数的比表示两个数相除。
新课讲解
1.关于比和比例的知识,你知道什么?它们有什么区别和联系?
比
意义 两个数相除又叫做这两个数的比。比表示两个数相除。
各部分名称 比由两项组成,比号前面的数叫做比的前项,比号后面的数叫做比的后项。
基本 性质 比的前项和后项同时乘或除以相同的数(0除外),比值不变。利用比的基本性质可以化简比。
化简比并求比值。
2.8 :3.5
朵朵
选一选。(将正确答案的序号填在括号里)[★★★]
(1)两个正方体的棱长比是2∶3,它的表面积之比是( )。
A.2∶3 B.4∶9 C.8∶27 D.4∶27
正方体的表面积=棱长×棱长×6
正方体表面积之比是棱长平方之比
表面积之比是(2×2):(3×3)
B
和
比 比例
意 义
各部分名称
基本性质
两个数的比表示两个数相 。
表示两个 相等的式子叫做比例。
0.6 ∶ 0.4
前项 后项
外项
内项
3: 2
0.6 : 0.4
=
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
在比例里,两个内项的积等于两个外项的积。
比
比例
除
比
5 : 8
5×8×3
8×5×3
= 8×5×3
×3
×3
15
: 24
=
新课讲解
你怎样判断两种相关联的量是成正比例关系还是成反比例关系?
正比例:两种相关联的量,其中一种量增加,另一种量也随着增加,一种量减少,另一种量也随着减少;两种量的比值一定。
反比例:两种相关联的量,其中一种量增加,另一种量反而减少,一种量减少,另一种量反而增加;两种量的积一定。
反比例:
xy=k(一定)
y
x
正比例:
=k(一定)
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做( )。它们的关系叫做( )。
如果用x和y表示两种相关联的量,用k表示它们的积,反比例关系可以用下面的式子表示:( )。
反比例
反比例关系
xy=k(一定)
把下面的比化成最简整数比,并求比值。[★★★]
∶ 0.25∶1.5 ∶ kg∶125 g
=2∶3
=1∶6
=11∶8
=8∶5
正、反比例的意义分别是什么?
正比例:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定。
反比例:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定。
课堂练习
植树节前夕,六年级同学来到山坡植树,原计划每人植树14棵,需要25人。实际每人植树10棵,还要增加多少人?
解:设还要增加x人。
14×25=10×(25+x)
x=10
答:还要增加10人。
A
两个数相除又叫做两个数的比。比的前项和后项同时乘(或除)相同的数(0除外)比值不变,这叫做基本性质。
B
表示两个比相等的式子叫作比例。在比例里,两个内项的积等于两个外项的积,这叫做比例的基本性质。
比和比例
C
正比例:
反比例:
x×y=k(一定)
水果超市原有苹果与梨的质量比是8∶3,苹果卖了 ,梨卖了50 kg后,苹果比梨多220 kg。水果超市原有苹果和梨共多少千克?[★★★★]
6.4-3
(220-50)÷( )
=50(kg)
50×(8+3)=550(kg)
答:水果超市原有苹果和梨共550kg。
水是由氢和氧按1 : 8 的质量比化合而成的。5.4 kg 的水含氢和氧各多少?
(教材第85页第3题)
判断每张表中的两种量是成正比例、反比例,还是不成比例,并说明理由。
成正比例, 因为比的前项和后项的比值一定。
成正比例, 因为小麦的质量和磨面粉质量的比值一定。
成反比例, 因为三角形的底和高的乘积一定。
不成比例,园的半径和面积的比值不一定。
总页数不变,即每天读的页数与天数的乘积一定
(教材第64页第8题)
小林读一本文学名著,如果每天读30页,8天可以读完,小林想6天读完,那么平均每天要读多少页?
每天读页数×天数 = 总页数(一定)
解:设平均每天要读x页。
6x=30×8
6x=240
x =40
答:平均每天要读40页。
解:设甲、乙两地之间的实际距离为x厘米。
1:25000 = 15:x
x = 15×25000
x = 375000
在比例尺是1:25000的地图上量得甲、乙两地之间的距离是15厘米,如果把它改画在比例尺为1:20000的地图上,甲、乙两地的图上距离应画多长?
同学们再见
