北师大版七下数学 第四章全等三角形解答题专练 (word版含答案)
文档属性
| 名称 | 北师大版七下数学 第四章全等三角形解答题专练 (word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 354.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-18 18:02:42 | ||
图片预览


文档简介
登录二一教育在线组卷平台 助您教考全无忧
全等三角形解答题专练
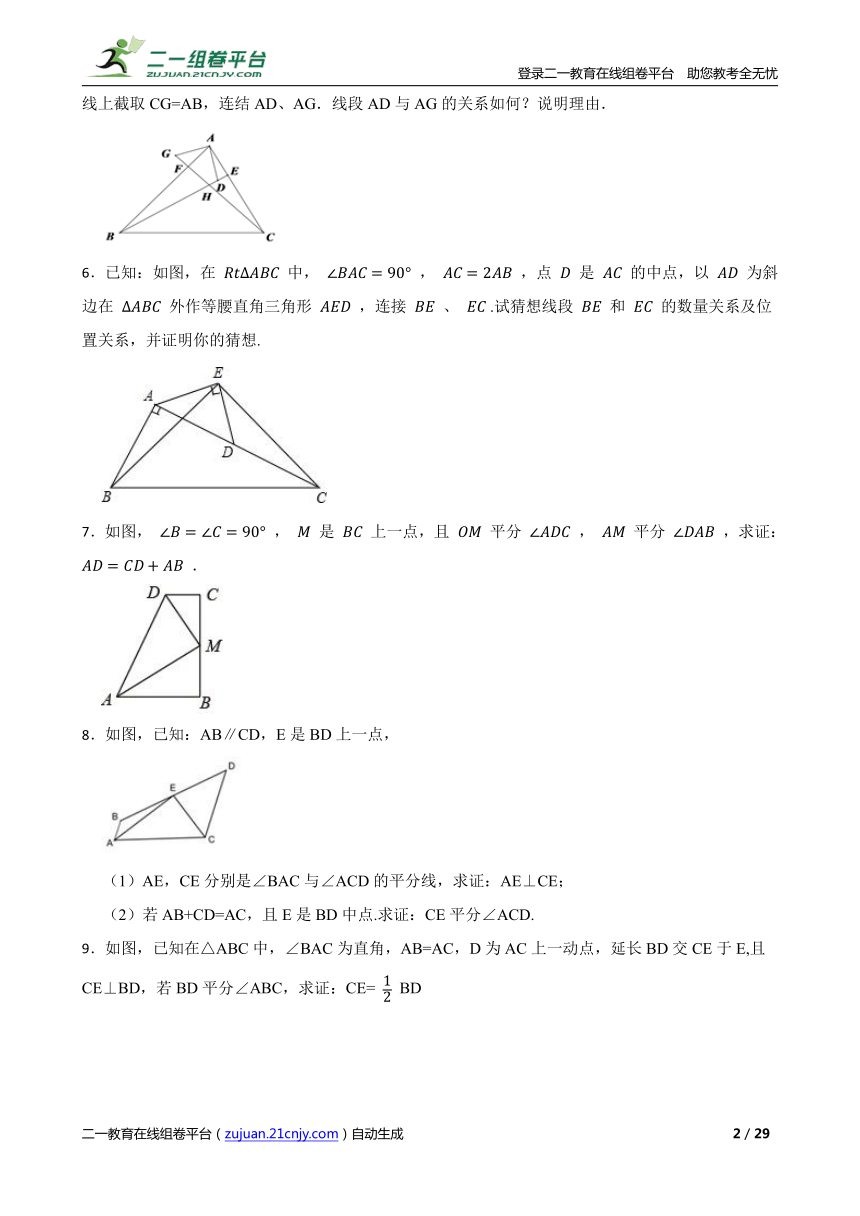
1.已知:Rt ABC中,∠B=90°,D是BC上一点,DF⊥BC交AC于点H,且DF=BC,FG⊥AC交BC于点E.求证:AB=DE.
2.如图,点D为锐角∠ABC的平分线上一点,点M在边BA上,点N在边BC上,∠BMD+∠BND=180°.试说明:DM=DN.
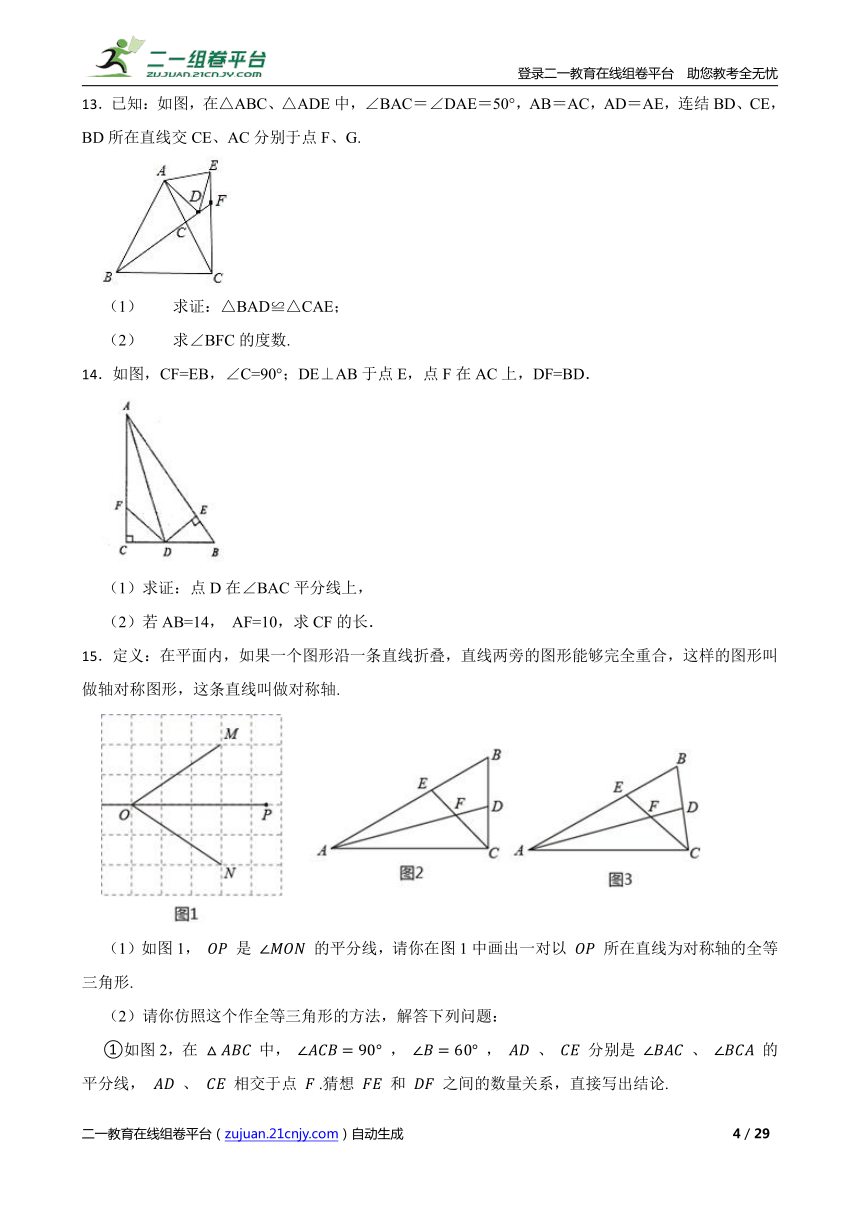
3.如图所示,点E在 外部,点D在BC边上,DE交AC于F,若 ,AD=AB,求证:AC=AE.
4.如图,已知 , ,求证 .
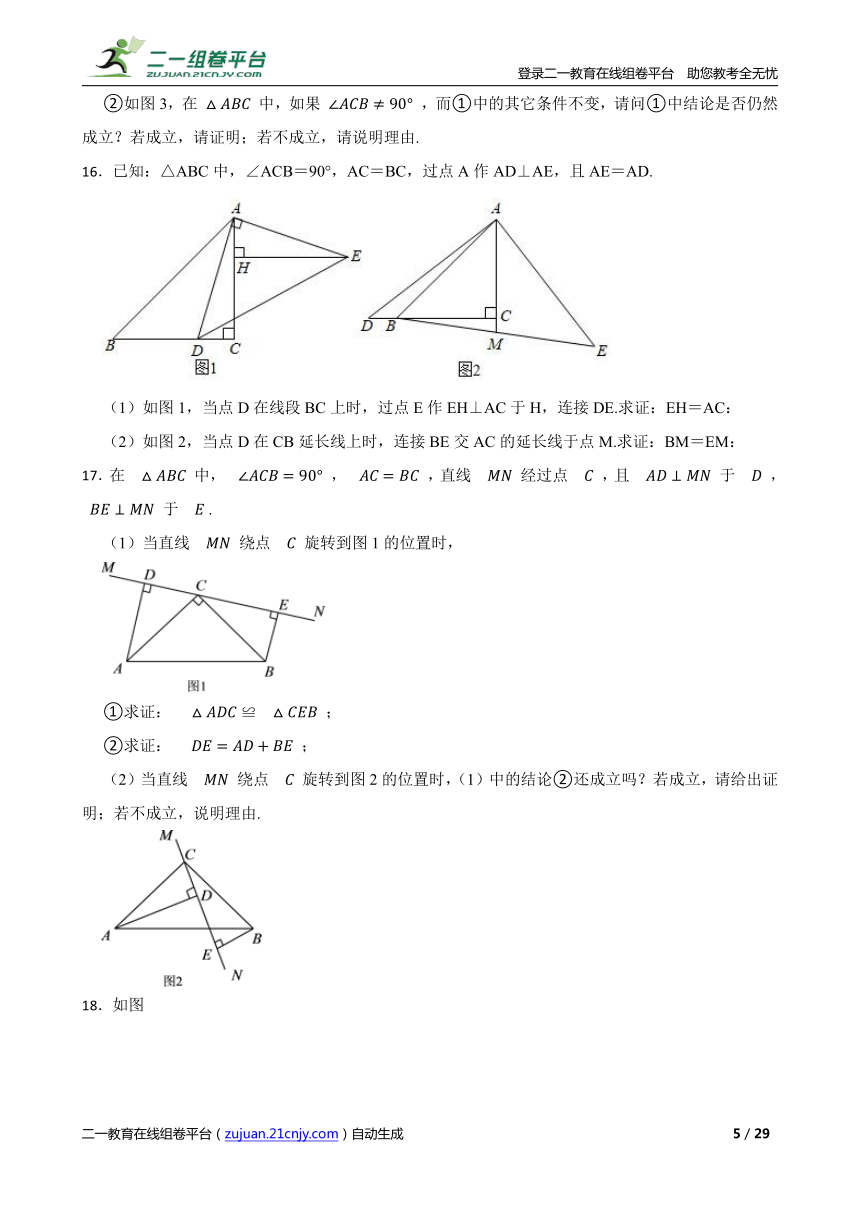
5.如图,在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连结AD、AG.线段AD与AG的关系如何?说明理由.
6.已知:如图,在 中, , ,点 是 的中点,以 为斜边在 外作等腰直角三角形 ,连接 、 .试猜想线段 和 的数量关系及位置关系,并证明你的猜想.
7.如图, , 是 上一点,且 平分 , 平分 ,求证: .
8.如图,已知:AB∥CD,E是BD上一点,
(1)AE,CE分别是∠BAC与∠ACD的平分线,求证:AE⊥CE;
(2)若AB+CD=AC,且E是BD中点.求证:CE平分∠ACD.
9.如图,已知在△ABC中,∠BAC为直角,AB=AC,D为AC上一动点,延长BD交CE于E,且CE⊥BD,若BD平分∠ABC,求证:CE= BD
10.如图,四边形 中, , , ,M、N分别为AB、AD上的动点,且 .求证: .
11.如图,在△ABC 和△DBC 中,∠ACB=∠DBC=90°,点 E 是 BC 的中点,DE⊥AB 于点F,且 AB=DE.
(1)求证:△ACB≌△EBD;
(2)若 DB=12,求 AC 的长.
12.如图,已知AD∥BC,点E是CD上一点,AE平分∠BAD,BF平分∠ABC,延长BE交AD的延长线于点F
(1)求证:△ABE≌△AFE;
(2)若AD=2,BC=6,求AB的长.
13.已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=50°,AB=AC,AD=AE,连结BD、CE,BD所在直线交CE、AC分别于点F、G.
(1)
求证:△BAD≌△CAE;
(2)
求∠BFC的度数.
14.如图,CF=EB,∠C=90°;DE⊥AB于点E,点F在AC上,DF=BD.
(1)求证:点D在∠BAC平分线上,
(2)若AB=14, AF=10,求CF的长.
15.定义:在平面内,如果一个图形沿一条直线折叠,直线两旁的图形能够完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴.
(1)如图1, 是 的平分线,请你在图1中画出一对以 所在直线为对称轴的全等三角形.
(2)请你仿照这个作全等三角形的方法,解答下列问题:
①如图2,在 中, , , 、 分别是 、 的平分线, 、 相交于点 .猜想 和 之间的数量关系,直接写出结论.
②如图3,在 中,如果 ,而①中的其它条件不变,请问①中结论是否仍然成立?若成立,请证明;若不成立,请说明理由.
16.已知:△ABC中,∠ACB=90°,AC=BC,过点A作AD⊥AE,且AE=AD.
(1)如图1,当点D在线段BC上时,过点E作EH⊥AC于H,连接DE.求证:EH=AC:
(2)如图2,当点D在CB延长线上时,连接BE交AC的延长线于点M.求证:BM=EM:
17.在
中,
,
,直线
经过点
,且
于
,
于
.
(1)当直线
绕点
旋转到图1的位置时,
①求证:
≌
;
②求证:
;
(2)当直线
绕点
旋转到图2的位置时,(1)中的结论②还成立吗?若成立,请给出证明;若不成立,说明理由.
18.如图
(1)如图1,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD,线段EF、BE、FD之间的关系是 ;(不需要证明)
(2)如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD,(1)中的结论是否仍然成立?若成立,请证明.若不成立,请写出它们之间的数量关系,并证明.
(3)如图3,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD延长线上的点,且∠EAF=∠BAD,(1)中的结论是否仍然成立?若成立,请证明.若不成立,请写出它们之间的数量关系,并证明.
19.(问题背景)
在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且∠EAF=60°,试探究图1中线段BE、EF、FD之间的数量关系。
(1)(初步探索)
小晨同学认为:延长FD到点G,使DG=BE,连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,则可得到BE、EF 、FD之间的数量关系是
(2)(探索延伸)
在四边形ABCD中如图2,AB=AD,∠B+∠D=180°,E、F分别是BC、CD上的
点,∠EAF= ∠BAD,上述结论是否仍然成立?说明理由。
(3)(结论运用)
如图3,在某次南海海域军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以80海里/小时的速度前进,舰艇乙沿北偏东50°的方向以100海里/小时的速度前进1.2小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角(∠EOF)为70°,试求此时两舰艇之间的距离。
20.八年级一班数学兴趣小组在一次活动中进行了探究试验活动,请你和他们一起活动吧.
(1)(探究与发现)
如图1,是的中线,延长至点,使,连接,写出图中全等的两个三角形
(2)(理解与应用)
填空:如图2,是的中线,若,,设,则的取值范围是 .
(3)已知:如图3,是的中线,,点在的延长线上,,求证:.
21.如图1,在△ABC中,若AB=10,BC=8,求AC边上的中线BD的取值范围.
(1)小聪同学是这样思考的:延长BD至E,使DE=BD,连接CE,可证得△CED≌△ABD.
①请证明△CED≌△ABD;
②中线BD的取值范围是
▲ .
(2)问题拓展:如图2,在△ABC中,点D是AC的中点,分别以AB,BC为直角边向△ABC外作等腰直角三角形ABM和等腰直角三角形BCN,其中,AB=BM,BC=BN,∠ABM=∠NBC=∠90°,连接MN.请写出BD与MN的数量关系,并说明理由.
22.如图
(1)如图1,∠MAN=90°,射线AE在这个角的内部,点B、C在∠MAN的边AM,AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.求证: .
(2)如图2,点B、C在∠MAN的边AM、AN上,点E、F在∠MAN内部射线AD上,∠1,∠2分别是 , 的外角,已知AB=AC,∠1=∠2=∠BAC,求证: ;
(3)如图3,在 中,AB=AC,AB>BC,点D在边BC上,CD=2BD,点E、F在线段AD上, ,若 的面积是15,则 与 的面积之和是 .
23.已知CD是经过∠BCA顶点C的一条直线,CA=CB.E、F分别是直线CD上两点,且∠BEC=∠CFA=∠ .
(1)若直线CD经过∠BCA的内部,且E、F在射线CD上,请解决下面问题:
①如图1若∠BCA=90°,∠ =90°、探索三条线段EF、BE、AF的数量关系并证明你的结论.
②如图2,若0°<∠BCA<180°, 请添加一个关于∠ 与∠BCA关系的条件,使①中的结论仍然成立;
(2)如图3,若直线CD经过∠BCA的外部,∠ =∠BCA,请写出三条线段EF、BE、AF的数量关系并证明你的结论.
24.综合与探究:问题情景:如图1所示,已知,在△ABC中,AC=BA,∠ACB=90°,AD是△ABC的中线,过点C作CE⊥AD,垂足为M,且交AB于点E.
(1)(探究一)小虎通过度量发现∠BCE=∠CAD,请你帮他说明理由;
(2)(探究二)小明在图中添加了一条线段CN,且CN平分∠ACB交AD于点N,如图2所示,即可得CN=BE,符合题意吗?请说明理由;
(3)(探究三)小刚在(2)的基础上,连接DE,如图3所示,又发现了一组全等三角形,你能发现吗?请找出来,并说明理由.
答案与解析
1.【答案】证明: DF⊥BC,FG⊥AC,
又∵
在 与 中
(ASA)
AB=DE.
2.【答案】解:过点D作DE⊥AB于点E,DF⊥BC于点F.
∴∠DEB=∠DFB=90°.
又∵BD平分∠ABC,
∴DE=DF.
∵∠BMD+∠DME=180°,∠BMD+∠BND=180°,
∴∠DME=∠BND.
在△EMD和△FND中,
,
∴△EMD≌△FND(AAS).
∴DM=DN.
3.【答案】证明: ,
,即 ,
由对顶角相等得: ,
又 ,
,
在 和 中, ,
,
.
4.【答案】证明: ,
,
即 ,
在 和 中,
,
,
.
5.【答案】解: BE、CF分别是AC、AB两边上的高,
,
在 与 中,
,
,
, ,
, ,
,
,
且 .
6.【答案】解: , .
证明: ,点 是 的中点,
,
,
,
在 和 中,
,
,
, ,
,
, .
7.【答案】证明:如图:
过 作 于 ,
, 平分 , 平分 ,
, , , , , ,
在 和 中,
,
,
,
同理:AE=AB,
.
8.【答案】(1)证明:∵AB//CD
∴∠BAC+∠DCA=180°
∵AE,CE分别是∠BAC与∠ACD的平分线,
∴∠EAC= ∠BAC,∠ECA= ∠DCA,
∴∠EAC+∠ECA= ∠BAC+ ∠DCA= (∠BAC+∠DCA)=90°.
∴∠AEC=180°-(∠EAC+∠ECA)=90°,
∴AE⊥BE
(2)解:延长CD交AE的延长线于点F,
∵AB//CD
∴∠FDB=∠B,∠F=∠BAF,
∵E是BD中点.
∴BE=ED,
∴△ABE≌△FDE,
∴AB=DF,AE=EF
∵AB+CD=AC,
∴CF=DF+CD=AB+CD=AC,
∵CE=CE,
∴△AEC≌△CFE,
∴∠ACE=∠FCE,
即CE平分∠ACD.
9.【答案】证明:延长CE、BA交于点F.
∵CE⊥BD于E,∠BAC=90°,
∴∠ABD=∠ACF.
在△ABD与△ACF中,
∵ ,
∴△ABD≌△ACF(ASA),
∴BD=CF.
∵BD平分∠ABC,
∴∠CBE=∠FBE.
在△BCE与△BFE中,
∵ ,
∴△BCE≌△BFE(ASA),
∴CE=EF,
即CE= CF,
∴CE= BD.
10.【答案】证明:延长 至点 ,使得 ,连接 ,
四边形 中, , ,
,
在 和 中,
,
,
, ,
, ,
,
,
在 和 中,
,
,
.
11.【答案】(1)解:,,
,
,
在和中,,
;
(2)解:由(1)已证:,
,
点是的中点,
,
.
12.【答案】(1)证明:∵AE、BE分别平分∠DAB、∠CBA,
∴∠BAE=∠EAF,∠ABF=∠EBC,
∵AD∥BC,
∴∠EBC=∠F,∠ABF=∠F,
在△ABE和△AFE中,
,
∴△ABE≌△AFE(AAS);
(2)解:∵△ABE≌△AFE,
∴BE=EF,
在△BCE和△FDE中,
,
∴△BCE≌△FDE(ASA),
∴BC=DF,
∴AD+BC=AD+DF=AF=AB,
即AD+BC=AB.
∵AD=2,BC=6,
∴AB=8.
13.【答案】(1) 证明:∵∠BAC=∠DAE,
∴∠BAC+∠CAD=∠EAD+∠CAD,
即∠BAD=∠EAC,
在△BAD与△CAE中,
,
∴△BAD≌△CAE(SAS),
(2) 解:∵△BAD≌△CAE,
∴∠ABD=∠ACE,
∵∠AGB=∠CGF,
∴∠BFC=∠BAC=50°
14.【答案】(1)证明:∵∠C=90°,DE⊥AB,
∴∠C=∠DEB=90°
在Rt△CDF与Rt△EDB中,
∴Rt△CDF≌Rt△EDB(HL),
∴DE=DC
∵∠C=90°,DE⊥AB,DE=DC
∴AD平分∠BAC
(2)解:设CF=BE=x,则AE=14-x,AC=10+x
在Rt△ACD与Rt△AED中,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,
∴10+x=14-x,解得x=2,
∴CF=2
15.【答案】(1)解:如图,△OQM与△OQN即为所求作,
∵OP是∠MON的平分线,
∴∠MOP=∠NOP,
∵OM=ON,OP= OP,
∴△OQM≌△OQN;
(2)解:①FE=FD.
如图,在AC上截取AG=AE,连接FG.
∵AD是∠BAC的平分线,
∴∠EAF=∠GAF,
在△EAF和△GAF中,
∵ ,
∴△EAF≌△GAF(SAS),
∴FE=FG,
∵∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,
∴∠FAC= ∠BAC,∠FCA= ∠ACB,且∠EAF=∠GAF,
∴∠FAC+∠FCA= (∠BAC+∠ACB)= (180°-∠B)=60°,
∴∠AFC=120°,
∴∠CFD=60°=∠CFG,
∴∠AFG=60°,
又∵∠EFA =∠CFD=60°,
∴∠EFA=∠GFA =60°,
在△FDC和△FGC中,
∵ ,
∴△FDC≌△FGC(ASA),
∴FD=FG.
∴FE=FD.
②结论FE=FD仍然成立.
在AC上截取 如图:
同①可得△EAF≌△HAF,
∴FE=FH,∠EFA=∠HFA.
∵∠FAC= ∠BAC,∠FCA= ∠ACB,
∴∠FAC+∠FCA= (∠BAC+∠ACB)= (180°-∠B)=60°.
∴∠AFC=180°-(∠FAC+∠FCA)=120°.
∴∠EFA=∠HFA=180°-120°=60°.
同①可得△FDC≌△FHC,
∴FD=FH.
∴FE=FD.
16.【答案】(1)证明:∵AD⊥AE,EH⊥AC,
∴∠AHE=∠EAD=∠ACB=90°,
∴∠DAC+∠ADC=90°,∠DAC+∠EAH=90°,
∴∠EAH=∠ADC,
又∵AD=AE,∠ACD=∠AHE=90°,
∴△AHE≌△DCA(AAS),
∴EH=AC;
(2)解:如图2,过点E作EN⊥AM,交AM的延长线于N,
∵AD⊥AE,EN⊥AM,
∴∠ANE=∠EAD=∠ACB=90°,
∴∠DAC+∠ADC=90°,∠DAC+∠EAN=90°,
∴∠EAN=∠ADC,
又∵AD=AE,∠ACD=∠ANE=90°,
∴△ANE≌△DCA(AAS),
∴EN=AC,
∵BC=AC,
∴BC=NE,
又∵∠BMC=∠EMN,∠BCM=∠ENM=90°,
∴△BCM≌△ENM(AAS),
∴BM=EM.
17.【答案】(1)证明:①∵AD⊥MN,BE⊥MN,
∴∠ADC=∠BEC=90°,
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,
∴∠DAC=∠BCE,
又∵AC=BC,
∴ ≌ ;
②∵ ≌ ,
∴CD=BE,AD=CE,
∵DE=CE+CD,
∴DE=AD+BE;
(2)解:DE=AD+BE不成立,此时应有DE=AD-BE,理由如下:
∵BE⊥MN,AD⊥MN,
∴∠ADC=∠BEC=90°,
∴∠EBC+∠ECB=90°,
∵∠ACB=90°,
∴∠ECB+∠ACE=90°,
∴∠ACD=∠EBC,
又∵AC=BC,
∴ ≌ ,
∴AD=CE,CD=BE,
∵DE=CE-CD,
∴DE=AD-BE.
18.【答案】(1)EF=BE+FD
(2)解:(1)中的结论仍然成立,
理由如下:如图2,延长CB至M,使BM=DF,连接AM,
∵∠ABC+∠D=180°,∠ABC+∠1=180°,
∴∠1=∠D,
在△ABM和△ADF中,
,
∴△ABM≌△ADF(SAS),
∴AM=AF,∠3=∠2,
∵∠EAF=∠BAD,
∴∠2+∠4=∠EAF,
∴∠EAM=∠3+∠4=∠2+∠4=∠EAF,
在△MAE和△FAE中,
,
∴△MAE≌△FAE(SAS),
∴EF=EM,
∵EM=BM+BE=BE+DF,
∴EF=BE+FD;
(3)解:(1)中的结论不成立,EF=BE﹣FD,
理由如下:如图3,在EB上截取BH=DF,连接AH,
同(2)中证法可得,△ABH≌△ADF,
∴AH=AF,∠BAH=∠DAF,
∴∠HAE=∠FAE,
在△HAE和△FAE中,
,
∴△HAE≌△FAE(SAS),
∵EH=BE﹣BH=BE﹣DF,
∴EF=BE﹣FD.
19.【答案】(1)
(2)结论仍然成立
证明:如图2,延长 到 ,使 ,连接 ,
∵ , ,
∴ ,
在 和 中, ,
∴ ,
∴ , ,
∵ ,
∴ ,
∴ ,
在 和 中, ,
∴ ,
∴ ,
∴ ,
∴ ;
(3)解:如图3,连接 ,延长 、 交于点 ,
∵ , ,
∴ ,
∵ , ,
∴符合探索延伸中的条件,
∴结论 成立,即 海里.
答:此时两舰艇之间的距离是216海里.
20.【答案】(1)
(2)
(3)证明:如图3,延长到,使,连接,
,
是的中线,
,
在与中,
,
,
,,
,
,,
,,
,
,
,
在与中,
,
,
.
21.【答案】(1)解:①∵BD是三角形ABC的中线,
∴AD=CD,
又∵∠ABD=∠CDE,BD=ED,
∴△CED≌△ABD(SAS);
②∵△CED≌△ABD,
∴AB=CE,
∵ ,
∴ 即 ,
又∵ ,
∴ ;
故答案为: ;
(2)MN=2BD,理由如下:
如图所示,延长BD到E使得DE=BD,
同(1)原理可证△ADE≌△CDB(SAS),
∴∠DAE=∠DCB,AE=CB,
∵BC=BN,
∴AE=BN,
∵∠ABM=∠NBC=90°,
∴∠MBN+∠ABC=360°-∠ABM-∠NBC=180°,
∵∠ABC+∠BAC+∠ACB=180°,
∴∠ABC+∠BAC+∠DAE=180°,
∴∠BAE+∠ABC=180°,
∴∠BAE=∠MBN,
又∵AB=BM,
∴△BAE≌△MBN(SAS),
∴MN=BE,
∵BE=BD+ED=2BD,
∴MN=2BD.
22.【答案】(1)证明:∵BD⊥AE,CF⊥AE
∴
∵
∴∠BAD+∠FAC=90°
∵∠FAC+∠ACF=90°
∴∠BAD=∠ACF
在△ABD与△CAF中
(2)证明:∵∠1=∠2,
∴∠AEB=∠CFA,
∵∠1=∠ABE+∠EAB,∠1=∠BAC,
∴∠ABE=∠CAF,
在△ABE与△CAF中
所以
(3)5
23.【答案】(1)①如图1中,.
.
E点在F点的左侧,.
∵BE⊥CD,AF⊥CD,∠ACB=90°,.
∴∠BEC=∠AFC=90°,.
∴∠BCE+∠ACF=90°,∠CBE+∠BCE=90°,.
∴∠CBE=∠ACF,.
在△BCE和△CAF中,.
,.
∴△BCE≌△CAF(AAS),.
∴BE=CF,CE=AF,.
∴EF=CF-CE=BE-AF,.
当E在F的右侧时,同理可证EF=AF-BE,.
∴EF=|BE-AF|;
②∠α+∠ACB=180°时,①中两个结论仍然成立;.
证明:如图2中,.
.
∵∠BEC=∠CFA=∠a,∠α+∠ACB=180°,.
∴∠CBE=∠ACF,.
在△BCE和△CAF中,.
,.
∴△BCE≌△CAF(AAS),.
∴BE=CF,CE=AF,.
∴EF=CF-CE=BE-AF,.
当E在F的右侧时,同理可证EF=AF-BE,.
∴EF=|BE-AF|;
(2)EF=BE+AF..
理由是:如图3中,.
.
∵∠BEC=∠CFA=∠a,∠a=∠BCA,.
又∵∠EBC+∠BCE+∠BEC=180°,∠BCE+∠ACF+∠ACB=180°,.
∴∠EBC+∠BCE=∠BCE+∠ACF,.
∴∠EBC=∠ACF,.
在△BEC和△CFA中,.
,.
∴△BEC≌△CFA(AAS),.
∴AF=CE,BE=CF,.
∵EF=CE+CF,.
∴EF=BE+AF.
24.【答案】(1)证明:如图1中,
,
,
,
, ,
.
(2)结论: 符合题意.
理由:如图2中,
平分 , ,
,
,
,
,
在 和 中,
,
,
.
(3)结论: .
理由: 是 的中点,
,
在 和 中,
,
.
二一教育在线组卷平台(zujuan.21cnjy.com)自动生成 1 / 1
全等三角形解答题专练
1.已知:Rt ABC中,∠B=90°,D是BC上一点,DF⊥BC交AC于点H,且DF=BC,FG⊥AC交BC于点E.求证:AB=DE.
2.如图,点D为锐角∠ABC的平分线上一点,点M在边BA上,点N在边BC上,∠BMD+∠BND=180°.试说明:DM=DN.
3.如图所示,点E在 外部,点D在BC边上,DE交AC于F,若 ,AD=AB,求证:AC=AE.
4.如图,已知 , ,求证 .
5.如图,在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连结AD、AG.线段AD与AG的关系如何?说明理由.
6.已知:如图,在 中, , ,点 是 的中点,以 为斜边在 外作等腰直角三角形 ,连接 、 .试猜想线段 和 的数量关系及位置关系,并证明你的猜想.
7.如图, , 是 上一点,且 平分 , 平分 ,求证: .
8.如图,已知:AB∥CD,E是BD上一点,
(1)AE,CE分别是∠BAC与∠ACD的平分线,求证:AE⊥CE;
(2)若AB+CD=AC,且E是BD中点.求证:CE平分∠ACD.
9.如图,已知在△ABC中,∠BAC为直角,AB=AC,D为AC上一动点,延长BD交CE于E,且CE⊥BD,若BD平分∠ABC,求证:CE= BD
10.如图,四边形 中, , , ,M、N分别为AB、AD上的动点,且 .求证: .
11.如图,在△ABC 和△DBC 中,∠ACB=∠DBC=90°,点 E 是 BC 的中点,DE⊥AB 于点F,且 AB=DE.
(1)求证:△ACB≌△EBD;
(2)若 DB=12,求 AC 的长.
12.如图,已知AD∥BC,点E是CD上一点,AE平分∠BAD,BF平分∠ABC,延长BE交AD的延长线于点F
(1)求证:△ABE≌△AFE;
(2)若AD=2,BC=6,求AB的长.
13.已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=50°,AB=AC,AD=AE,连结BD、CE,BD所在直线交CE、AC分别于点F、G.
(1)
求证:△BAD≌△CAE;
(2)
求∠BFC的度数.
14.如图,CF=EB,∠C=90°;DE⊥AB于点E,点F在AC上,DF=BD.
(1)求证:点D在∠BAC平分线上,
(2)若AB=14, AF=10,求CF的长.
15.定义:在平面内,如果一个图形沿一条直线折叠,直线两旁的图形能够完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴.
(1)如图1, 是 的平分线,请你在图1中画出一对以 所在直线为对称轴的全等三角形.
(2)请你仿照这个作全等三角形的方法,解答下列问题:
①如图2,在 中, , , 、 分别是 、 的平分线, 、 相交于点 .猜想 和 之间的数量关系,直接写出结论.
②如图3,在 中,如果 ,而①中的其它条件不变,请问①中结论是否仍然成立?若成立,请证明;若不成立,请说明理由.
16.已知:△ABC中,∠ACB=90°,AC=BC,过点A作AD⊥AE,且AE=AD.
(1)如图1,当点D在线段BC上时,过点E作EH⊥AC于H,连接DE.求证:EH=AC:
(2)如图2,当点D在CB延长线上时,连接BE交AC的延长线于点M.求证:BM=EM:
17.在
中,
,
,直线
经过点
,且
于
,
于
.
(1)当直线
绕点
旋转到图1的位置时,
①求证:
≌
;
②求证:
;
(2)当直线
绕点
旋转到图2的位置时,(1)中的结论②还成立吗?若成立,请给出证明;若不成立,说明理由.
18.如图
(1)如图1,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD,线段EF、BE、FD之间的关系是 ;(不需要证明)
(2)如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD,(1)中的结论是否仍然成立?若成立,请证明.若不成立,请写出它们之间的数量关系,并证明.
(3)如图3,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD延长线上的点,且∠EAF=∠BAD,(1)中的结论是否仍然成立?若成立,请证明.若不成立,请写出它们之间的数量关系,并证明.
19.(问题背景)
在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且∠EAF=60°,试探究图1中线段BE、EF、FD之间的数量关系。
(1)(初步探索)
小晨同学认为:延长FD到点G,使DG=BE,连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,则可得到BE、EF 、FD之间的数量关系是
(2)(探索延伸)
在四边形ABCD中如图2,AB=AD,∠B+∠D=180°,E、F分别是BC、CD上的
点,∠EAF= ∠BAD,上述结论是否仍然成立?说明理由。
(3)(结论运用)
如图3,在某次南海海域军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以80海里/小时的速度前进,舰艇乙沿北偏东50°的方向以100海里/小时的速度前进1.2小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角(∠EOF)为70°,试求此时两舰艇之间的距离。
20.八年级一班数学兴趣小组在一次活动中进行了探究试验活动,请你和他们一起活动吧.
(1)(探究与发现)
如图1,是的中线,延长至点,使,连接,写出图中全等的两个三角形
(2)(理解与应用)
填空:如图2,是的中线,若,,设,则的取值范围是 .
(3)已知:如图3,是的中线,,点在的延长线上,,求证:.
21.如图1,在△ABC中,若AB=10,BC=8,求AC边上的中线BD的取值范围.
(1)小聪同学是这样思考的:延长BD至E,使DE=BD,连接CE,可证得△CED≌△ABD.
①请证明△CED≌△ABD;
②中线BD的取值范围是
▲ .
(2)问题拓展:如图2,在△ABC中,点D是AC的中点,分别以AB,BC为直角边向△ABC外作等腰直角三角形ABM和等腰直角三角形BCN,其中,AB=BM,BC=BN,∠ABM=∠NBC=∠90°,连接MN.请写出BD与MN的数量关系,并说明理由.
22.如图
(1)如图1,∠MAN=90°,射线AE在这个角的内部,点B、C在∠MAN的边AM,AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.求证: .
(2)如图2,点B、C在∠MAN的边AM、AN上,点E、F在∠MAN内部射线AD上,∠1,∠2分别是 , 的外角,已知AB=AC,∠1=∠2=∠BAC,求证: ;
(3)如图3,在 中,AB=AC,AB>BC,点D在边BC上,CD=2BD,点E、F在线段AD上, ,若 的面积是15,则 与 的面积之和是 .
23.已知CD是经过∠BCA顶点C的一条直线,CA=CB.E、F分别是直线CD上两点,且∠BEC=∠CFA=∠ .
(1)若直线CD经过∠BCA的内部,且E、F在射线CD上,请解决下面问题:
①如图1若∠BCA=90°,∠ =90°、探索三条线段EF、BE、AF的数量关系并证明你的结论.
②如图2,若0°<∠BCA<180°, 请添加一个关于∠ 与∠BCA关系的条件,使①中的结论仍然成立;
(2)如图3,若直线CD经过∠BCA的外部,∠ =∠BCA,请写出三条线段EF、BE、AF的数量关系并证明你的结论.
24.综合与探究:问题情景:如图1所示,已知,在△ABC中,AC=BA,∠ACB=90°,AD是△ABC的中线,过点C作CE⊥AD,垂足为M,且交AB于点E.
(1)(探究一)小虎通过度量发现∠BCE=∠CAD,请你帮他说明理由;
(2)(探究二)小明在图中添加了一条线段CN,且CN平分∠ACB交AD于点N,如图2所示,即可得CN=BE,符合题意吗?请说明理由;
(3)(探究三)小刚在(2)的基础上,连接DE,如图3所示,又发现了一组全等三角形,你能发现吗?请找出来,并说明理由.
答案与解析
1.【答案】证明: DF⊥BC,FG⊥AC,
又∵
在 与 中
(ASA)
AB=DE.
2.【答案】解:过点D作DE⊥AB于点E,DF⊥BC于点F.
∴∠DEB=∠DFB=90°.
又∵BD平分∠ABC,
∴DE=DF.
∵∠BMD+∠DME=180°,∠BMD+∠BND=180°,
∴∠DME=∠BND.
在△EMD和△FND中,
,
∴△EMD≌△FND(AAS).
∴DM=DN.
3.【答案】证明: ,
,即 ,
由对顶角相等得: ,
又 ,
,
在 和 中, ,
,
.
4.【答案】证明: ,
,
即 ,
在 和 中,
,
,
.
5.【答案】解: BE、CF分别是AC、AB两边上的高,
,
在 与 中,
,
,
, ,
, ,
,
,
且 .
6.【答案】解: , .
证明: ,点 是 的中点,
,
,
,
在 和 中,
,
,
, ,
,
, .
7.【答案】证明:如图:
过 作 于 ,
, 平分 , 平分 ,
, , , , , ,
在 和 中,
,
,
,
同理:AE=AB,
.
8.【答案】(1)证明:∵AB//CD
∴∠BAC+∠DCA=180°
∵AE,CE分别是∠BAC与∠ACD的平分线,
∴∠EAC= ∠BAC,∠ECA= ∠DCA,
∴∠EAC+∠ECA= ∠BAC+ ∠DCA= (∠BAC+∠DCA)=90°.
∴∠AEC=180°-(∠EAC+∠ECA)=90°,
∴AE⊥BE
(2)解:延长CD交AE的延长线于点F,
∵AB//CD
∴∠FDB=∠B,∠F=∠BAF,
∵E是BD中点.
∴BE=ED,
∴△ABE≌△FDE,
∴AB=DF,AE=EF
∵AB+CD=AC,
∴CF=DF+CD=AB+CD=AC,
∵CE=CE,
∴△AEC≌△CFE,
∴∠ACE=∠FCE,
即CE平分∠ACD.
9.【答案】证明:延长CE、BA交于点F.
∵CE⊥BD于E,∠BAC=90°,
∴∠ABD=∠ACF.
在△ABD与△ACF中,
∵ ,
∴△ABD≌△ACF(ASA),
∴BD=CF.
∵BD平分∠ABC,
∴∠CBE=∠FBE.
在△BCE与△BFE中,
∵ ,
∴△BCE≌△BFE(ASA),
∴CE=EF,
即CE= CF,
∴CE= BD.
10.【答案】证明:延长 至点 ,使得 ,连接 ,
四边形 中, , ,
,
在 和 中,
,
,
, ,
, ,
,
,
在 和 中,
,
,
.
11.【答案】(1)解:,,
,
,
在和中,,
;
(2)解:由(1)已证:,
,
点是的中点,
,
.
12.【答案】(1)证明:∵AE、BE分别平分∠DAB、∠CBA,
∴∠BAE=∠EAF,∠ABF=∠EBC,
∵AD∥BC,
∴∠EBC=∠F,∠ABF=∠F,
在△ABE和△AFE中,
,
∴△ABE≌△AFE(AAS);
(2)解:∵△ABE≌△AFE,
∴BE=EF,
在△BCE和△FDE中,
,
∴△BCE≌△FDE(ASA),
∴BC=DF,
∴AD+BC=AD+DF=AF=AB,
即AD+BC=AB.
∵AD=2,BC=6,
∴AB=8.
13.【答案】(1) 证明:∵∠BAC=∠DAE,
∴∠BAC+∠CAD=∠EAD+∠CAD,
即∠BAD=∠EAC,
在△BAD与△CAE中,
,
∴△BAD≌△CAE(SAS),
(2) 解:∵△BAD≌△CAE,
∴∠ABD=∠ACE,
∵∠AGB=∠CGF,
∴∠BFC=∠BAC=50°
14.【答案】(1)证明:∵∠C=90°,DE⊥AB,
∴∠C=∠DEB=90°
在Rt△CDF与Rt△EDB中,
∴Rt△CDF≌Rt△EDB(HL),
∴DE=DC
∵∠C=90°,DE⊥AB,DE=DC
∴AD平分∠BAC
(2)解:设CF=BE=x,则AE=14-x,AC=10+x
在Rt△ACD与Rt△AED中,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,
∴10+x=14-x,解得x=2,
∴CF=2
15.【答案】(1)解:如图,△OQM与△OQN即为所求作,
∵OP是∠MON的平分线,
∴∠MOP=∠NOP,
∵OM=ON,OP= OP,
∴△OQM≌△OQN;
(2)解:①FE=FD.
如图,在AC上截取AG=AE,连接FG.
∵AD是∠BAC的平分线,
∴∠EAF=∠GAF,
在△EAF和△GAF中,
∵ ,
∴△EAF≌△GAF(SAS),
∴FE=FG,
∵∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,
∴∠FAC= ∠BAC,∠FCA= ∠ACB,且∠EAF=∠GAF,
∴∠FAC+∠FCA= (∠BAC+∠ACB)= (180°-∠B)=60°,
∴∠AFC=120°,
∴∠CFD=60°=∠CFG,
∴∠AFG=60°,
又∵∠EFA =∠CFD=60°,
∴∠EFA=∠GFA =60°,
在△FDC和△FGC中,
∵ ,
∴△FDC≌△FGC(ASA),
∴FD=FG.
∴FE=FD.
②结论FE=FD仍然成立.
在AC上截取 如图:
同①可得△EAF≌△HAF,
∴FE=FH,∠EFA=∠HFA.
∵∠FAC= ∠BAC,∠FCA= ∠ACB,
∴∠FAC+∠FCA= (∠BAC+∠ACB)= (180°-∠B)=60°.
∴∠AFC=180°-(∠FAC+∠FCA)=120°.
∴∠EFA=∠HFA=180°-120°=60°.
同①可得△FDC≌△FHC,
∴FD=FH.
∴FE=FD.
16.【答案】(1)证明:∵AD⊥AE,EH⊥AC,
∴∠AHE=∠EAD=∠ACB=90°,
∴∠DAC+∠ADC=90°,∠DAC+∠EAH=90°,
∴∠EAH=∠ADC,
又∵AD=AE,∠ACD=∠AHE=90°,
∴△AHE≌△DCA(AAS),
∴EH=AC;
(2)解:如图2,过点E作EN⊥AM,交AM的延长线于N,
∵AD⊥AE,EN⊥AM,
∴∠ANE=∠EAD=∠ACB=90°,
∴∠DAC+∠ADC=90°,∠DAC+∠EAN=90°,
∴∠EAN=∠ADC,
又∵AD=AE,∠ACD=∠ANE=90°,
∴△ANE≌△DCA(AAS),
∴EN=AC,
∵BC=AC,
∴BC=NE,
又∵∠BMC=∠EMN,∠BCM=∠ENM=90°,
∴△BCM≌△ENM(AAS),
∴BM=EM.
17.【答案】(1)证明:①∵AD⊥MN,BE⊥MN,
∴∠ADC=∠BEC=90°,
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,
∴∠DAC=∠BCE,
又∵AC=BC,
∴ ≌ ;
②∵ ≌ ,
∴CD=BE,AD=CE,
∵DE=CE+CD,
∴DE=AD+BE;
(2)解:DE=AD+BE不成立,此时应有DE=AD-BE,理由如下:
∵BE⊥MN,AD⊥MN,
∴∠ADC=∠BEC=90°,
∴∠EBC+∠ECB=90°,
∵∠ACB=90°,
∴∠ECB+∠ACE=90°,
∴∠ACD=∠EBC,
又∵AC=BC,
∴ ≌ ,
∴AD=CE,CD=BE,
∵DE=CE-CD,
∴DE=AD-BE.
18.【答案】(1)EF=BE+FD
(2)解:(1)中的结论仍然成立,
理由如下:如图2,延长CB至M,使BM=DF,连接AM,
∵∠ABC+∠D=180°,∠ABC+∠1=180°,
∴∠1=∠D,
在△ABM和△ADF中,
,
∴△ABM≌△ADF(SAS),
∴AM=AF,∠3=∠2,
∵∠EAF=∠BAD,
∴∠2+∠4=∠EAF,
∴∠EAM=∠3+∠4=∠2+∠4=∠EAF,
在△MAE和△FAE中,
,
∴△MAE≌△FAE(SAS),
∴EF=EM,
∵EM=BM+BE=BE+DF,
∴EF=BE+FD;
(3)解:(1)中的结论不成立,EF=BE﹣FD,
理由如下:如图3,在EB上截取BH=DF,连接AH,
同(2)中证法可得,△ABH≌△ADF,
∴AH=AF,∠BAH=∠DAF,
∴∠HAE=∠FAE,
在△HAE和△FAE中,
,
∴△HAE≌△FAE(SAS),
∵EH=BE﹣BH=BE﹣DF,
∴EF=BE﹣FD.
19.【答案】(1)
(2)结论仍然成立
证明:如图2,延长 到 ,使 ,连接 ,
∵ , ,
∴ ,
在 和 中, ,
∴ ,
∴ , ,
∵ ,
∴ ,
∴ ,
在 和 中, ,
∴ ,
∴ ,
∴ ,
∴ ;
(3)解:如图3,连接 ,延长 、 交于点 ,
∵ , ,
∴ ,
∵ , ,
∴符合探索延伸中的条件,
∴结论 成立,即 海里.
答:此时两舰艇之间的距离是216海里.
20.【答案】(1)
(2)
(3)证明:如图3,延长到,使,连接,
,
是的中线,
,
在与中,
,
,
,,
,
,,
,,
,
,
,
在与中,
,
,
.
21.【答案】(1)解:①∵BD是三角形ABC的中线,
∴AD=CD,
又∵∠ABD=∠CDE,BD=ED,
∴△CED≌△ABD(SAS);
②∵△CED≌△ABD,
∴AB=CE,
∵ ,
∴ 即 ,
又∵ ,
∴ ;
故答案为: ;
(2)MN=2BD,理由如下:
如图所示,延长BD到E使得DE=BD,
同(1)原理可证△ADE≌△CDB(SAS),
∴∠DAE=∠DCB,AE=CB,
∵BC=BN,
∴AE=BN,
∵∠ABM=∠NBC=90°,
∴∠MBN+∠ABC=360°-∠ABM-∠NBC=180°,
∵∠ABC+∠BAC+∠ACB=180°,
∴∠ABC+∠BAC+∠DAE=180°,
∴∠BAE+∠ABC=180°,
∴∠BAE=∠MBN,
又∵AB=BM,
∴△BAE≌△MBN(SAS),
∴MN=BE,
∵BE=BD+ED=2BD,
∴MN=2BD.
22.【答案】(1)证明:∵BD⊥AE,CF⊥AE
∴
∵
∴∠BAD+∠FAC=90°
∵∠FAC+∠ACF=90°
∴∠BAD=∠ACF
在△ABD与△CAF中
(2)证明:∵∠1=∠2,
∴∠AEB=∠CFA,
∵∠1=∠ABE+∠EAB,∠1=∠BAC,
∴∠ABE=∠CAF,
在△ABE与△CAF中
所以
(3)5
23.【答案】(1)①如图1中,.
.
E点在F点的左侧,.
∵BE⊥CD,AF⊥CD,∠ACB=90°,.
∴∠BEC=∠AFC=90°,.
∴∠BCE+∠ACF=90°,∠CBE+∠BCE=90°,.
∴∠CBE=∠ACF,.
在△BCE和△CAF中,.
,.
∴△BCE≌△CAF(AAS),.
∴BE=CF,CE=AF,.
∴EF=CF-CE=BE-AF,.
当E在F的右侧时,同理可证EF=AF-BE,.
∴EF=|BE-AF|;
②∠α+∠ACB=180°时,①中两个结论仍然成立;.
证明:如图2中,.
.
∵∠BEC=∠CFA=∠a,∠α+∠ACB=180°,.
∴∠CBE=∠ACF,.
在△BCE和△CAF中,.
,.
∴△BCE≌△CAF(AAS),.
∴BE=CF,CE=AF,.
∴EF=CF-CE=BE-AF,.
当E在F的右侧时,同理可证EF=AF-BE,.
∴EF=|BE-AF|;
(2)EF=BE+AF..
理由是:如图3中,.
.
∵∠BEC=∠CFA=∠a,∠a=∠BCA,.
又∵∠EBC+∠BCE+∠BEC=180°,∠BCE+∠ACF+∠ACB=180°,.
∴∠EBC+∠BCE=∠BCE+∠ACF,.
∴∠EBC=∠ACF,.
在△BEC和△CFA中,.
,.
∴△BEC≌△CFA(AAS),.
∴AF=CE,BE=CF,.
∵EF=CE+CF,.
∴EF=BE+AF.
24.【答案】(1)证明:如图1中,
,
,
,
, ,
.
(2)结论: 符合题意.
理由:如图2中,
平分 , ,
,
,
,
,
在 和 中,
,
,
.
(3)结论: .
理由: 是 的中点,
,
在 和 中,
,
.
二一教育在线组卷平台(zujuan.21cnjy.com)自动生成 1 / 1
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
