12.3等腰三角形课时作业(附答案)
文档属性
| 名称 | 12.3等腰三角形课时作业(附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 132.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-09 14:28:15 | ||
图片预览



文档简介
12.3等腰三角形课时作业(附答案)
姓名:_______________班级:_______________考号:_______________
一、选择题
1、已知等腰三角形的一个底角为40°,则这个等腰三角形的顶角为( ???)
A.40°?? ????B.100° ???C.40°或100°?????? D.50°或70°
2、如图,,, 若,则的度数是(?? )
A.? 15°??? B.? 20°????? C.? 25°?????? D.? 30°
3、等腰三角形的两条边长分别为3,6,那么它的周长为( )
A.15??????? B.12??????? C.12或15????????? D.不能确定
4、如图,一个等边三角形的边长与和它的一边相切的圆的周长相等,当这个圆按箭头方向从某一位置沿等边三角形的三边做无滑动旋转,直至回到原出发位置时,问该圆转的圈数是( )
A.1 B.2 C.3 D.4
5、一等腰三角形的两边长是方程x2-5x+6=0的两根,则这等腰三角形的周长为(??? )
A.7 ???B.8??? ? ?C. 7或8?? ????D.不能确定
6、已知等腰三角形的两条边长分别是2和4,则它的周长是????????????????????? ( ???)
A.8?????????????B.10??? ?????????C.8或10????? ????D.无法确定
7、已知等腰三角形的两条边长分别为3和7,则它的周长为( )
A、10? ??????B、13???? ?????C、17???? ?????D、13或17
8、到三角形三条边的距离都相等的点是这个三角形的(??? )
A.三条中线的交点;
B.三条高线的交点;
C.三条角平分线的交点;
D.三条边的中垂线的交点。
9、已知一个等腰三角形两内角的度数之比为,则这个等腰三角形顶角的度数为(??? )
A.???? B.???? C.或?????? D.
10、等腰三角形的两边长是2和5,它的周长是
A.9????????????? B.12???????????? C.9或12????????? D.7
二、填空题
11、在直角三角形中,若两条直角边长分别为6cm和8cm, 则斜边上的中线长为?????????? ?cm.
12、已知:如图△ABC中,AB=AC,∠C=30°,AB⊥AD,AD=4,则 BC =????? .
13、若等腰三角形的一个角是,则其底角为 .
14、如图,P、Q是△ABC边BC上的两点,且BP=PQ=QC=AP=AQ,则∠BAC=?????????? ???。
15、已知底边a和底边上的高h,在用尺规作图方法作这个等腰△CDE,使DE=a,CB=h时,需用到的作法有:
①在MN上截取BC=h;
②作线段DE=a;
③作线段DE的垂直平分线MN,与DE交于点B;
④连接CD,CE,△CDE就是所求的等腰三角形.则正确作图步骤的序号是???? .
16、在△ABC中,若∠B=∠C=2∠A,则∠C=_______.
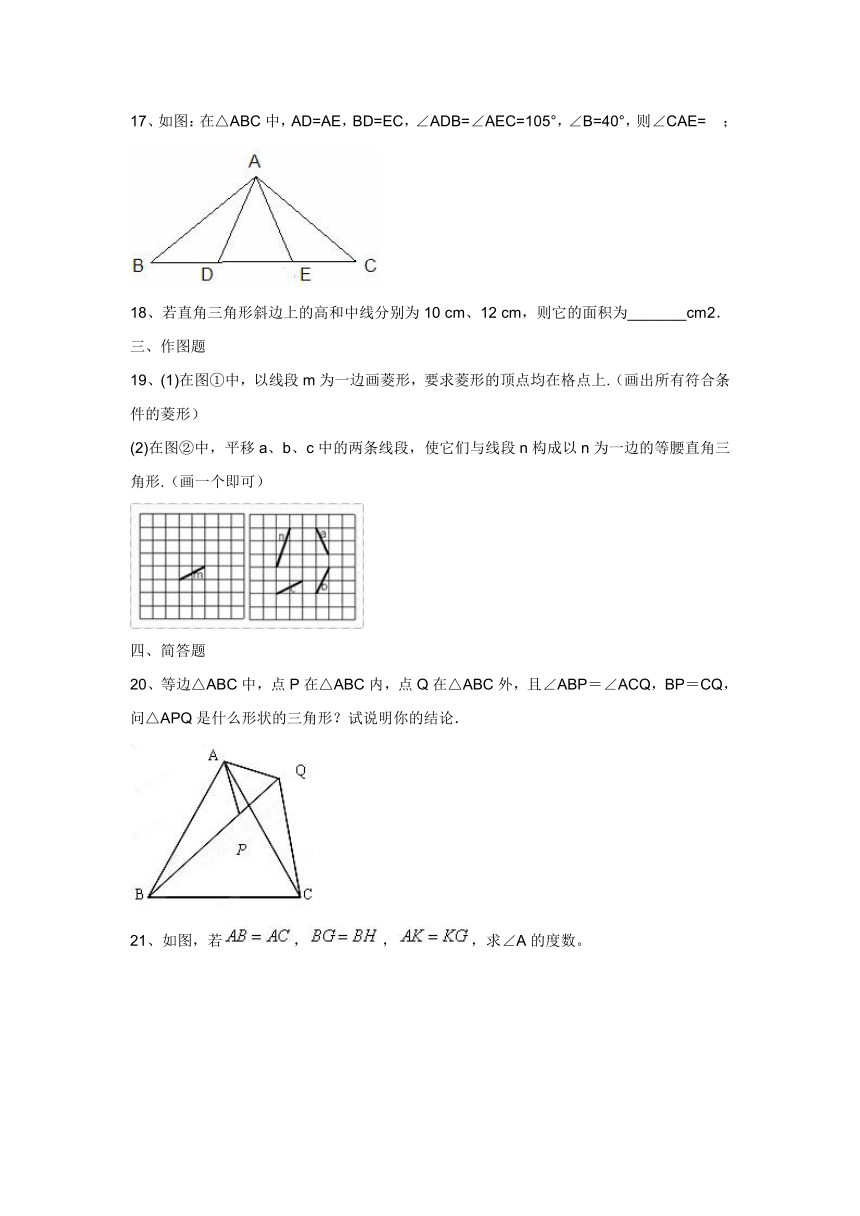
17、如图:在△ABC中,AD=AE,BD=EC,∠ADB=∠AEC=105°,∠B=40°,则∠CAE=?? ;
18、若直角三角形斜边上的高和中线分别为10 cm、12 cm,则它的面积为_______cm2.
三、作图题
19、(1)在图①中,以线段m为一边画菱形,要求菱形的顶点均在格点上.(画出所有符合条件的菱形)
(2)在图②中,平移a、b、c中的两条线段,使它们与线段n构成以n为一边的等腰直角三角形.(画一个即可)
四、简答题
20、等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,问△APQ是什么形状的三角形?试说明你的结论.
21、如图,若,,,求∠A的度数。
22、如图A、B在方格纸的格点位置上。
(1)请再找一个格点C,使它们所构成的三角形为轴对称图形;
(2)这样的格点C在右图中共有???? 个。
23、已知:在△ABC中,∠ABC=-90°,点B在直线AB上,ED与直线AC垂直,垂足为D,且点M为EC中点,连接BM,DM.
(1)如图1,若点E在线段AB上,探究线段BM与DM及∠BMD与∠BCD所满足的数量关系,并直接写出你得到的结论;
(2)如图2,若点E在BA延长线上,你在(1)中得到的结论是否发生变化?写出你的猜想并加以证明:
(3)若点E在AB延长线上,请你根据条件画出相应的图形,并直接写出线段BM与DM及∠BMD与∠BCD所满足的数量关系.
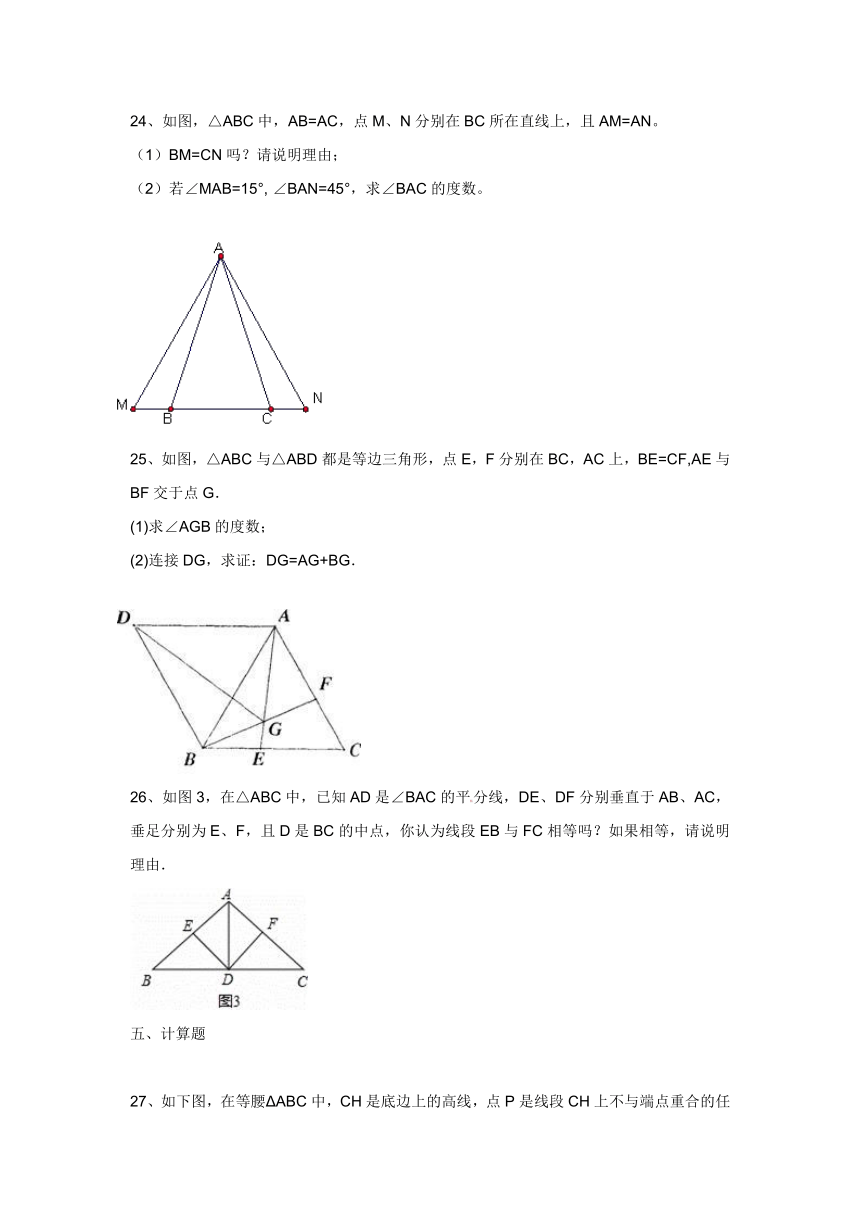
24、如图,△ABC中,AB=AC,点M、N分别在BC所在直线上,且AM=AN。
(1)BM=CN吗?请说明理由;
(2)若∠MAB=15°, ∠BAN=45°,求∠BAC的度数。
25、如图,△ABC与△ABD都是等边三角形,点E,F分别在BC,AC上,BE=CF,AE与BF交于点G.
(1)求∠AGB的度数;
(2)连接DG,求证:DG=AG+BG.
26、如图3,在△ABC中,已知AD是∠BAC的平分线,DE、DF分别垂直于AB、AC,垂足分别为E、F,且D是BC的中点,你认为线段EB与FC相等吗?如果相等,请说明理由.
五、计算题
27、如下图,在等腰ΔABC中,CH是底边上的高线,点P是线段CH上不与端点重合的任意一点,连结AP交BC于点E,连结BP交AC于点F。
(1)证明:∠CAE=∠CBF;
(2)证明:AE=BF;
(3)以线段AE,BF和AB为边构成一个新的三角形ABG(点E与点F重合于点G),记ΔABC和ΔABG的面积分别为SΔABC和SΔABG,如果存在点P,能使SΔABC=SΔABG,求∠C的取值范围。
28、(1)已知中,,,请画一条直线,把这个三角形分割成两个等腰三角形.(请你选用下面给出的备用图,把所有不同的分割方法都画出来.只需画图,不必说明理由,但要在图中标出相等两角的度数)
(2)已知中,是其最小的内角,过顶点的一条直线把这个三角形分割成了两个等腰三角形,请探求与之间的关系.
参考答案
一、选择题
1、B
2、A
3、A
4、C
5、C
6、B
7、C
8、C
9、C
10、B;
二、填空题
11、5
12、12
13、70°或55°
14、120
15、②③①④;
16、?
17、35°
18、120
三、作图题
19、操作与实践(本题5分)
注:(1)小题画对6个4分,5个3分,4个2分,2个1分
四、简答题
20、等边三角形
21、36°
22、10个
23、解:(1)结论:BM=DM,∠BMD=2∠BCD.
(2)在(1)中得到的结论仍然成立.即BM=DM,∠BMD=2∠BCD.
证法一:∵点M是Rt△BEC的斜边EC的中点,
∴BM=EC=MC,
又点M是Rt△DEC的斜边EC的中点,
∴DM=EC=MC.
∴BM=DM.
∵BM=MC,BM=MC,
∴∠CBM=∠BCM,∠DCM=∠CDM.
∴∠BMD=∠EMB-∠EMD=2∠BCM-2∠DCM
=2(∠BCM-∠DCM)=2∠BCD.
即∠BMD=2∠BCD.
证法二:∵点M是Rt△BEC的斜边EC的中点,
∴BM=EC=ME.
又点M是Rt△DEC的斜边EC的中点,
∴DM=EC=MC,
∴BM=DM.
∵BM=ME,DM=MC,
∴∠BEC=∠EBM,∠MCD=∠MDC.
∴∠BEM+∠MCD=∠BAC=90°-∠BCD.
∴∠BMD=180°-(∠BMC+∠DME)
=180°-2(∠BEM+∠MCD)=180°-2(90°-∠BCD)=2∠BCD.
即∠BMD=2∠BCD.
(3)所画图形如图所示:
图1中有BM=DM,∠BMD=2∠BCD;
图2中∠BCD不存在,有BM=DM;
图3中有BM=DM,∠BMD=360°-2∠BCD.
24、(1)过点A作AD⊥MN于点D,利用等腰三角形的三线合一,易得BD=CD,MD=ND,再由等式的性质可得结论:BM=CN.
(2) ∠BAC=30°
理由:
25、(1)∵△ABC是等边三角形 ∴AB=BC?? ∠ABC=∠C=60°
∵BE=CF? ∴△ABE≌△BCF?????? 2分 ∴∠BAE=∠FBC
∵∠BGE=∠ABG+∠BAE=∠ABG+∠FBC=∠ABC=60°
∴∠AGB=180°- ∠BGE=120°??
(2)延长GE至点H,使GH=GB
∵∠BGE=60°∴△BGH为等边三角形???????
∴BG=BH=GH??? ∠GBH=60°
∵△ABD是等边三角形 ∴AB=BD?? ∠ABD=60°
∵∠ABH =∠GBH+∠ABG?? ∠DBG=∠ABD+∠ABG
∴∠ABH=∠DBG? ??
∵AB=BD ,BG=BH???? ∴△DBG≌△ABH? ?
∴ DG=AH=AG+GH=AG+BG ???????
26、解:相等,
∵AD是∠BAC的平分线,DE⊥AB,DF⊥AC,
∴DE=DF,
在Rt△BED和Rt△CFD中,
∵DE=DF,BD=DC,
∴Rt△BED≌Rt△CFD(HL),
∴EB=FC.
五、计算题
27、证明:(1) ∵△是等腰△,是底边上的高线,∴,
又∵, ∴△ ≌△,
∴, 即;
(2) ∵, ,,
∴△ ≌△,∴;
(3) 由(2)知△是以为底边的等腰△,∴ 等价于,
1)当∠为直角或钝角时,在△中,不论点在何处,均有,所以结论不成立;
2)当∠为锐角时, ∠,而,要使,只需使∠ =∠,此时,∠180°2∠,
只须180°2∠∠,解得 60°∠ 90°.
28、解:(1)如图
(2)设,,过点的直线交边于.在中,
①若是顶角,如图1,则,
,.
此时只能有,即,
,即.
②若是底角,则有两种情况.
第一种情况:如图2,当时,则,
中,,.
1.由,得,此时有,即.
2.由,得,此时,即.
3.由,得,此时,即,为小于的任意锐角.
第二种情况,如图3,当时,,,此时只能有,
从而,这与题设是最小角矛盾.
当是底角时,不成立.
姓名:_______________班级:_______________考号:_______________
一、选择题
1、已知等腰三角形的一个底角为40°,则这个等腰三角形的顶角为( ???)
A.40°?? ????B.100° ???C.40°或100°?????? D.50°或70°
2、如图,,, 若,则的度数是(?? )
A.? 15°??? B.? 20°????? C.? 25°?????? D.? 30°
3、等腰三角形的两条边长分别为3,6,那么它的周长为( )
A.15??????? B.12??????? C.12或15????????? D.不能确定
4、如图,一个等边三角形的边长与和它的一边相切的圆的周长相等,当这个圆按箭头方向从某一位置沿等边三角形的三边做无滑动旋转,直至回到原出发位置时,问该圆转的圈数是( )
A.1 B.2 C.3 D.4
5、一等腰三角形的两边长是方程x2-5x+6=0的两根,则这等腰三角形的周长为(??? )
A.7 ???B.8??? ? ?C. 7或8?? ????D.不能确定
6、已知等腰三角形的两条边长分别是2和4,则它的周长是????????????????????? ( ???)
A.8?????????????B.10??? ?????????C.8或10????? ????D.无法确定
7、已知等腰三角形的两条边长分别为3和7,则它的周长为( )
A、10? ??????B、13???? ?????C、17???? ?????D、13或17
8、到三角形三条边的距离都相等的点是这个三角形的(??? )
A.三条中线的交点;
B.三条高线的交点;
C.三条角平分线的交点;
D.三条边的中垂线的交点。
9、已知一个等腰三角形两内角的度数之比为,则这个等腰三角形顶角的度数为(??? )
A.???? B.???? C.或?????? D.
10、等腰三角形的两边长是2和5,它的周长是
A.9????????????? B.12???????????? C.9或12????????? D.7
二、填空题
11、在直角三角形中,若两条直角边长分别为6cm和8cm, 则斜边上的中线长为?????????? ?cm.
12、已知:如图△ABC中,AB=AC,∠C=30°,AB⊥AD,AD=4,则 BC =????? .
13、若等腰三角形的一个角是,则其底角为 .
14、如图,P、Q是△ABC边BC上的两点,且BP=PQ=QC=AP=AQ,则∠BAC=?????????? ???。
15、已知底边a和底边上的高h,在用尺规作图方法作这个等腰△CDE,使DE=a,CB=h时,需用到的作法有:
①在MN上截取BC=h;
②作线段DE=a;
③作线段DE的垂直平分线MN,与DE交于点B;
④连接CD,CE,△CDE就是所求的等腰三角形.则正确作图步骤的序号是???? .
16、在△ABC中,若∠B=∠C=2∠A,则∠C=_______.
17、如图:在△ABC中,AD=AE,BD=EC,∠ADB=∠AEC=105°,∠B=40°,则∠CAE=?? ;
18、若直角三角形斜边上的高和中线分别为10 cm、12 cm,则它的面积为_______cm2.
三、作图题
19、(1)在图①中,以线段m为一边画菱形,要求菱形的顶点均在格点上.(画出所有符合条件的菱形)
(2)在图②中,平移a、b、c中的两条线段,使它们与线段n构成以n为一边的等腰直角三角形.(画一个即可)
四、简答题
20、等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,问△APQ是什么形状的三角形?试说明你的结论.
21、如图,若,,,求∠A的度数。
22、如图A、B在方格纸的格点位置上。
(1)请再找一个格点C,使它们所构成的三角形为轴对称图形;
(2)这样的格点C在右图中共有???? 个。
23、已知:在△ABC中,∠ABC=-90°,点B在直线AB上,ED与直线AC垂直,垂足为D,且点M为EC中点,连接BM,DM.
(1)如图1,若点E在线段AB上,探究线段BM与DM及∠BMD与∠BCD所满足的数量关系,并直接写出你得到的结论;
(2)如图2,若点E在BA延长线上,你在(1)中得到的结论是否发生变化?写出你的猜想并加以证明:
(3)若点E在AB延长线上,请你根据条件画出相应的图形,并直接写出线段BM与DM及∠BMD与∠BCD所满足的数量关系.
24、如图,△ABC中,AB=AC,点M、N分别在BC所在直线上,且AM=AN。
(1)BM=CN吗?请说明理由;
(2)若∠MAB=15°, ∠BAN=45°,求∠BAC的度数。
25、如图,△ABC与△ABD都是等边三角形,点E,F分别在BC,AC上,BE=CF,AE与BF交于点G.
(1)求∠AGB的度数;
(2)连接DG,求证:DG=AG+BG.
26、如图3,在△ABC中,已知AD是∠BAC的平分线,DE、DF分别垂直于AB、AC,垂足分别为E、F,且D是BC的中点,你认为线段EB与FC相等吗?如果相等,请说明理由.
五、计算题
27、如下图,在等腰ΔABC中,CH是底边上的高线,点P是线段CH上不与端点重合的任意一点,连结AP交BC于点E,连结BP交AC于点F。
(1)证明:∠CAE=∠CBF;
(2)证明:AE=BF;
(3)以线段AE,BF和AB为边构成一个新的三角形ABG(点E与点F重合于点G),记ΔABC和ΔABG的面积分别为SΔABC和SΔABG,如果存在点P,能使SΔABC=SΔABG,求∠C的取值范围。
28、(1)已知中,,,请画一条直线,把这个三角形分割成两个等腰三角形.(请你选用下面给出的备用图,把所有不同的分割方法都画出来.只需画图,不必说明理由,但要在图中标出相等两角的度数)
(2)已知中,是其最小的内角,过顶点的一条直线把这个三角形分割成了两个等腰三角形,请探求与之间的关系.
参考答案
一、选择题
1、B
2、A
3、A
4、C
5、C
6、B
7、C
8、C
9、C
10、B;
二、填空题
11、5
12、12
13、70°或55°
14、120
15、②③①④;
16、?
17、35°
18、120
三、作图题
19、操作与实践(本题5分)
注:(1)小题画对6个4分,5个3分,4个2分,2个1分
四、简答题
20、等边三角形
21、36°
22、10个
23、解:(1)结论:BM=DM,∠BMD=2∠BCD.
(2)在(1)中得到的结论仍然成立.即BM=DM,∠BMD=2∠BCD.
证法一:∵点M是Rt△BEC的斜边EC的中点,
∴BM=EC=MC,
又点M是Rt△DEC的斜边EC的中点,
∴DM=EC=MC.
∴BM=DM.
∵BM=MC,BM=MC,
∴∠CBM=∠BCM,∠DCM=∠CDM.
∴∠BMD=∠EMB-∠EMD=2∠BCM-2∠DCM
=2(∠BCM-∠DCM)=2∠BCD.
即∠BMD=2∠BCD.
证法二:∵点M是Rt△BEC的斜边EC的中点,
∴BM=EC=ME.
又点M是Rt△DEC的斜边EC的中点,
∴DM=EC=MC,
∴BM=DM.
∵BM=ME,DM=MC,
∴∠BEC=∠EBM,∠MCD=∠MDC.
∴∠BEM+∠MCD=∠BAC=90°-∠BCD.
∴∠BMD=180°-(∠BMC+∠DME)
=180°-2(∠BEM+∠MCD)=180°-2(90°-∠BCD)=2∠BCD.
即∠BMD=2∠BCD.
(3)所画图形如图所示:
图1中有BM=DM,∠BMD=2∠BCD;
图2中∠BCD不存在,有BM=DM;
图3中有BM=DM,∠BMD=360°-2∠BCD.
24、(1)过点A作AD⊥MN于点D,利用等腰三角形的三线合一,易得BD=CD,MD=ND,再由等式的性质可得结论:BM=CN.
(2) ∠BAC=30°
理由:
25、(1)∵△ABC是等边三角形 ∴AB=BC?? ∠ABC=∠C=60°
∵BE=CF? ∴△ABE≌△BCF?????? 2分 ∴∠BAE=∠FBC
∵∠BGE=∠ABG+∠BAE=∠ABG+∠FBC=∠ABC=60°
∴∠AGB=180°- ∠BGE=120°??
(2)延长GE至点H,使GH=GB
∵∠BGE=60°∴△BGH为等边三角形???????
∴BG=BH=GH??? ∠GBH=60°
∵△ABD是等边三角形 ∴AB=BD?? ∠ABD=60°
∵∠ABH =∠GBH+∠ABG?? ∠DBG=∠ABD+∠ABG
∴∠ABH=∠DBG? ??
∵AB=BD ,BG=BH???? ∴△DBG≌△ABH? ?
∴ DG=AH=AG+GH=AG+BG ???????
26、解:相等,
∵AD是∠BAC的平分线,DE⊥AB,DF⊥AC,
∴DE=DF,
在Rt△BED和Rt△CFD中,
∵DE=DF,BD=DC,
∴Rt△BED≌Rt△CFD(HL),
∴EB=FC.
五、计算题
27、证明:(1) ∵△是等腰△,是底边上的高线,∴,
又∵, ∴△ ≌△,
∴, 即;
(2) ∵, ,,
∴△ ≌△,∴;
(3) 由(2)知△是以为底边的等腰△,∴ 等价于,
1)当∠为直角或钝角时,在△中,不论点在何处,均有,所以结论不成立;
2)当∠为锐角时, ∠,而,要使,只需使∠ =∠,此时,∠180°2∠,
只须180°2∠∠,解得 60°∠ 90°.
28、解:(1)如图
(2)设,,过点的直线交边于.在中,
①若是顶角,如图1,则,
,.
此时只能有,即,
,即.
②若是底角,则有两种情况.
第一种情况:如图2,当时,则,
中,,.
1.由,得,此时有,即.
2.由,得,此时,即.
3.由,得,此时,即,为小于的任意锐角.
第二种情况,如图3,当时,,,此时只能有,
从而,这与题设是最小角矛盾.
当是底角时,不成立.
