沪科版数学八年级下册20.2数据的集中趋势与离散程度(第一课时)课件 (共32张PPT)
文档属性
| 名称 | 沪科版数学八年级下册20.2数据的集中趋势与离散程度(第一课时)课件 (共32张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 611.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-18 18:05:40 | ||
图片预览






文档简介
(共32张PPT)
第1课时 平均数
一、数据的集中趋势
导入新课
讲授新课
当堂练习
课堂小结
沪科版数学八年级下册
20.2 数据的集中趋势与离散程度
当你听到“小亮的身高在班上是中等偏上的”,“A 篮球队队员比B 队更年轻”等诸如此类的说法时,你思考过这些话的含义吗?你知道人们是如何作出这一判断的吗?
导入新课
数据2、3、4、1、2的平均数是________,这个平均数叫做_________平均数.
2.4
算术
日常生活中,我们常用平均数表示一组数据的“平均水平”
新课导入
样本平均数估计总体平均数
测试 第1次 第2次 第3次 第4次 第5次 第6次 第7次 第8次
小明 10 10 11 10 14 16 16 17
小华 11 12 12 12 14 13 15 13
问题2、小明和小华参加某体育项目的训练,近期的8次测试成绩(单位:分)如表:
若从这选一人参加市中学生运动会,从平均水平的角度考虑你认为选谁去合适
新课导入
问题1、数据2、3、4、1、2的平均数是________,
还记得小学如何计算平均数吗?
2.4
计算两人的平均成绩
(10+10+11+10+14+16+16+17)÷8=13
(11+12+12+12+14+13+15+13)÷8=12.75
从平均水平的角度考虑选小明去较合适
记为 ,读作:“x拔”.
算术平均数
定义:
一般地,对于n个数x1,x2,…,xn,我们 把 (x1+x2+…+xn)叫做这n个数的算术平均数;简称平均数
讲授新课
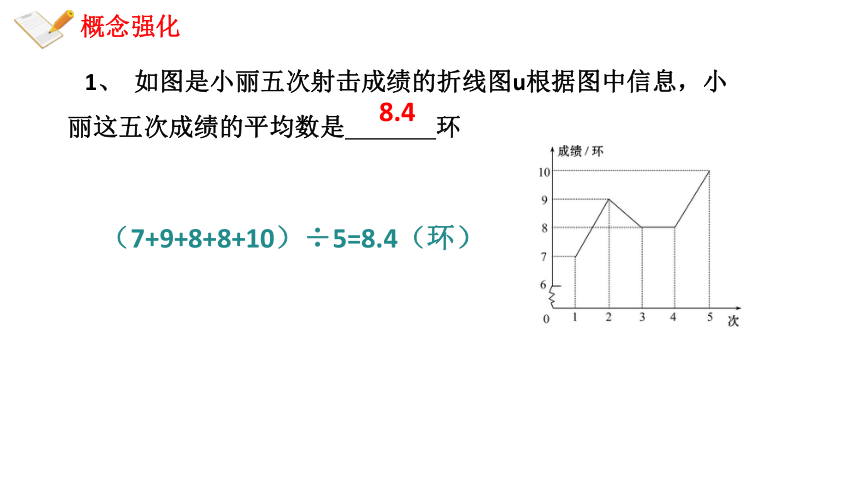
1、 如图是小丽五次射击成绩的折线图u根据图中信息,小丽这五次成绩的平均数是 环
概念强化
(7+9+8+8+10)÷5=8.4(环)
8.4
2、 为了估计某矿区铁矿石的含铁量,抽取了15块矿石,测得它们的含铁量如下:(单位:%)
26 24 21 28 27 23 23 25
26 22 21 30 26 20 30
则样本的平均数是多少 估计这个矿区铁矿石的平均含铁量约为多少
概念强化
答:估计这个矿区铁矿石的平均含铁量约为24.8%
样本的平均数
样本平均数估计总体平均数
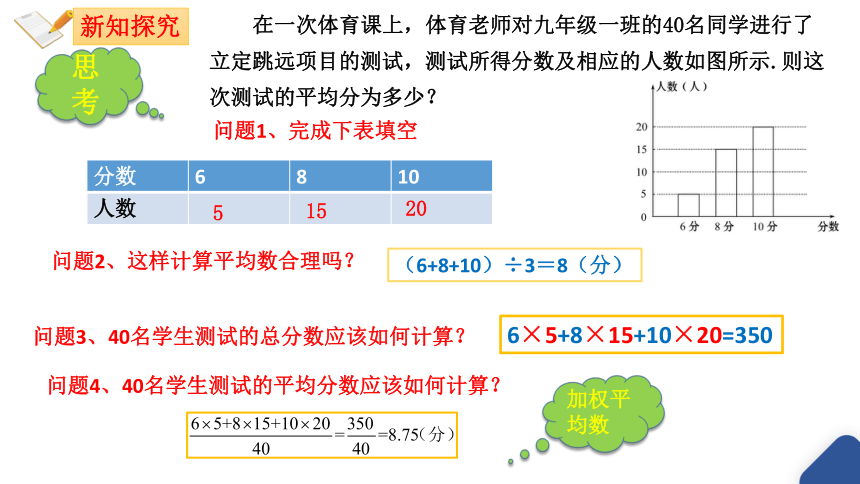
在一次体育课上,体育老师对九年级一班的40名同学进行了立定跳远项目的测试,测试所得分数及相应的人数如图所示.则这次测试的平均分为多少?
新知探究
思考
问题1、完成下表填空
分数 6 8 10
人数
5
15
20
问题2、这样计算平均数合理吗?
(6+8+10)÷3=8(分)
问题3、40名学生测试的总分数应该如何计算?
6×5+8×15+10×20=350
问题4、40名学生测试的平均分数应该如何计算?
加权平均数
在求n个数的算术平均数时,如果x1出现f1次,x2出现f2次,…,xk出现fk次(这里f1+f2+…+fk=n)那么这n个数的算术平均数
也叫做x1,x2,…,xk这k个数的加权平均数,其中f1,f2,…,fk分别叫做x1,x2,…,xk的权。
加权平均数
新知讲解
例1 植树节到了, 某单位组织职工开展植树竞赛, 下图反映的是植树量与人数之间的关系.
3
4
5
6
7
8
棵数
12
10
8
6
4
2
0
人数
0
请根据图中信息计算:
(1)总共有多少人参加了本次活动?
(2)总共植树多少棵?
(3)平均每人植树多少棵?
例题讲授
(3)平均每人植树:155÷32≈4.8 (棵)
解:
(1)参加本次活动的总人数:
1+8+1+10+8+3+1=32(人)
(2)总共植树:3×8+4×1+5×10+6×8+7×3+8×1=155(棵).
0
2
4
6
8
10
12
14
40
50
60
70
80
90
频数
周长/cm
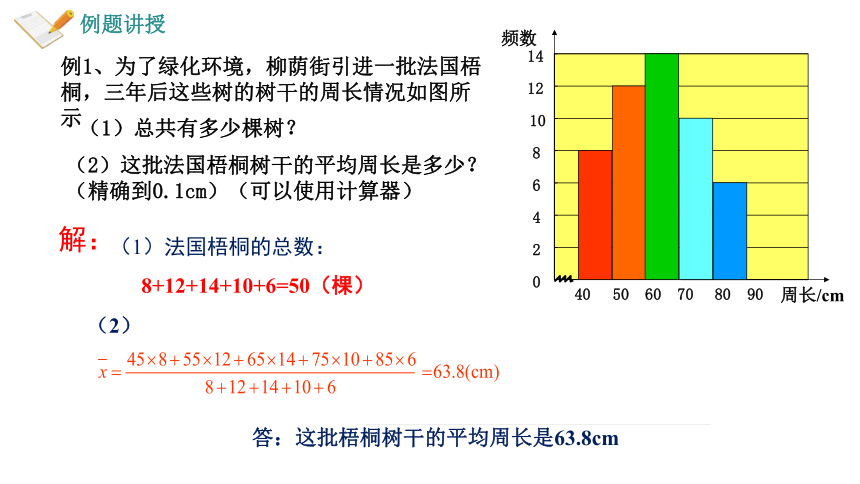
例1、为了绿化环境,柳荫街引进一批法国梧桐,三年后这些树的树干的周长情况如图所示
答:这批梧桐树干的平均周长是63.8cm
(1)总共有多少棵树?
(2)这批法国梧桐树干的平均周长是多少?(精确到0.1cm)(可以使用计算器)
解:
例题讲授
(1)法国梧桐的总数:
8+12+14+10+6=50(棵)
(2)
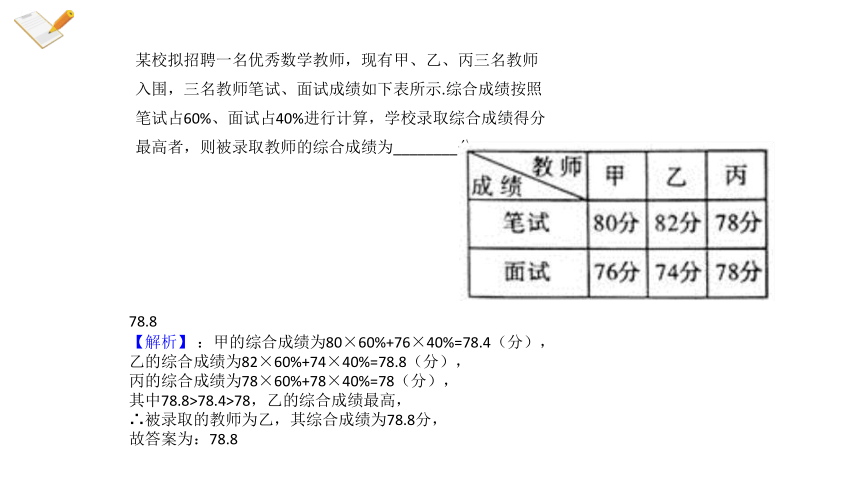
某校拟招聘一名优秀数学教师,现有甲、乙、丙三名教师入围,三名教师笔试、面试成绩如下表所示.综合成绩按照笔试占60%、面试占40%进行计算,学校录取综合成绩得分最高者,则被录取教师的综合成绩为________分.
78.8
【解析】 :甲的综合成绩为80×60%+76×40%=78.4(分),乙的综合成绩为82×60%+74×40%=78.8(分),
丙的综合成绩为78×60%+78×40%=78(分),
其中78.8>78.4>78,乙的综合成绩最高,
∴被录取的教师为乙,其综合成绩为78.8分,
故答案为:78.8
测试选手 测试成绩
创新 唱功 综合知识
甲 72 85 67
乙 85 74 70
∴按三项平均值取第一名选手乙为第一名
解:(1)
某次歌唱比赛,两名选手的成绩如下:
讲授新课
(1)甲、乙三项平均值谁高 若按三项平均值取第一名,则谁是第一名?
(3)若三项测试得分按3:6:1的比例确定个人的测试成绩,此时第一名是谁?
(2)这样确定第一名的方法科学吗
>
(2)不科学,因为创新、唱功、综合知识这三项在表现选手综合水平里所占的重要性不一样
讨论
(3)
此时第一名是选手甲
概念二:
一般地,若n个数x1,x2,…,xn的权分别 是w1,w2,…,wn ,则这n个数
据的加权平均数为
=
讲授新课
在实际问题中,一组数据里的各个数据的“重要程度” 未必相同.因而,在计算这组数据的平均数时,往往给每个数据一个“权”.
加权平均数
根据实际需要对不同类型的数据赋予与其重要程度相应的比例,称为这组数据的权.
权
权重的意义:
加权平均数的意义:
各个数据在该组数据中所占有的不同重要性的反映.
按各个数据的权重来反映该组数据的总体平均大小情况.
例题讲授
例2、某校拟招聘一名优秀数学教师,现有甲、乙、丙三名教师入围,三名教师笔试、面试成绩如下表所示.综合成绩按照笔试占60%、面试占40%进行计算,学校录取综合成绩得分最高者,则被录取教师的综合成绩为多少分.
权
教师 成绩(分) 甲 乙 丙
笔试 80 82 78
面试 76 74 78
∵78.8>78.4>78,
乙的综合成绩最高,
∴被录取的教师为乙,其综合成绩为78.8分,
解:
甲的综合成绩:
乙的综合成绩:
丙的综合成绩:
概念总结
1、加权平均数就是把数据按照合理的比例来计算。
2.“权”就是“权重”、“比重”的意思
3. 加权平均数=数与该数权的积的和÷权之和
4. “权”的常见形式
(1)数据的形式:如50、45、55
(2)比的形式:如3:3:2:2
(3)百分比的形式:如50%、40%、10%
加权平均数
1. 平均数计算:
算术平均数=各数据的和÷数据的个数
2. 平均数的意义:
算术平均数反映一组数据总体的平均大小情况.
加权平均数反映一组数据中按各数据占有的不同权重时总体的平均大小情况.
3. 区别:
加权平均数=(各数据×该数据的权重)的和÷总权数
算术平均数中各数据都是同等的重要, 没有相互间差异;
加权平均数中各数据都有各自不同的权重地位,彼此之间存在差异性的区别.
算术平均数与加权平均数的比较
概念总结
考试 测试1 测试2 测试3 期中 期末
成绩 89 78 85 90 87
例3、 小青在七年级第二学期的数学成绩如下表格, 请按图示的测试、期中、期末的权重, 计算小青同学该学期总评成绩
期中
30%
期末
60%
平时
10%
解:
先计算小青的平时成绩:
(89+78+85)÷3
= 84
再计算小青的总评成绩:
84×10%+ 90×30%+ 87×60%
= 87.6 (分)
例题讲授
1、某校生物兴趣小组11人到校外采集植物标本,其中2人每人采集到6件,4人每人采集到3件,5人每人采集到4件,则这个兴趣小组平均每人采集标本( )
A、3件 B、4件 C、5件 D、6件
2、10名学生的平均成绩是x,如果另外5名学生
平均成绩得84分,那么这15人的平均成绩是( )
A、 B、
C、 D、
B
B
课堂练习
3.李大伯有一片果林,共有80棵果树.某日,李大伯开始采摘今年第一批成熟的果子,他随机选取2棵果树共摘得10个果子,质量分别为(单位:㎏):0.28,0.26,0.24,0.23,0.25,0.24,0.26,0.26,0.25,0.23.以此估算,李大伯收获的这批果子的单个质量和总质量分别约为( )
A.0.25 ㎏,200 ㎏ B.2.5 ㎏,100 ㎏
C.0.25 ㎏,100 ㎏ D.2.5 ㎏,200 ㎏
C
课堂练习
4、某商场用加权平均数来确定什锦糖的单价,由单价为15元/千克的甲种糖果10千克,单价为12元/千克的乙种糖果20千克,单价为10元/千克的丙种糖果30千克混合成的什锦糖果的单价应定为( )
(A)11元/千克 (B)11.5元/千克
(C)12元/千克 (D)12.5元/千克
B
5、某商场6月份随机调查了6天的营业额,结果分别如下(单位:万元):2.8,3.2,3.4,3.0,3.1,3.7,试估算该商场6月份的总营业额大约是( )
(A)84万元 (B)96万元 (C)93万元 (D)111万元
B
由此可估计该商场6月份总营业额大约是3.2×30=96(万元)
=3.2(万元)
课堂练习
6、有五盒火柴,每盒火柴的根数如下:71 、73、 76、 77 、78
则每盒火柴的平均根数是___.
7、5个数据的和为405,其中一个数据为85,那么另4个数据的平均数是 _.
8、小明来学校的路程是100米,速度是5米/秒,回家的路程是100米,速度是2.5米/秒,在整个过程中的平均速度是:_____
课堂练习
75
80
200÷(100÷5+100÷2.5)=(米/秒)
总路程÷总时间=平均速度
9、老师对同学们每学期总评成绩时,并不是简单地将一个学生的平时成绩与考试成绩相加除以2而是按照“平时练习占 40%, 考试成绩占60% ”的比例计算,其中考试成绩更为重要.这样,如果一个学生的平时成绩为70分,考试成绩为90分,那么他的学期总评成绩就应该为多少呢?
课堂练习
解:
该同学的学期总评成绩是:
70×30%+90×60%
=82(分)
年龄/岁 13 14 15 16
频数 1 4 5 2
求校女子排球队队员的平均年龄(结果取整数).
解:
答:校女子排球队队员的平均年龄为15岁
10、下表是校女子排球队队员的年龄分布.
课堂练习
1、某次舞蹈大赛的记分规则为:从七位评委的打分中去掉一个最高分和一个最低分后计算平均分作为最后得分.以下是在该次比赛中七位评委对小菲与小岚的打分情况(单位:分):
提升练习
请通过计算说明谁的最后得分高.
小菲 80 77 82 83 75 78 89
小岚 79 80 77 76 82 85 81
解:小菲去掉一个最高分89分,去掉一个最低分75分,最后得分为
小岚去掉一个最高分85分,去掉一个最低分76分,最后得分为
∵80分>79.8分,∴小菲的最后得分高
2、一家公司打算招聘一名英文翻译,对甲、乙两名应试者进行了听、说、读、写的英语水平测试,他们各项的成绩(百分制)如下:
应试者 听 说 读 写
甲 85 83 78 75
乙 73 80 85 82
如果这家公司想招一名口语能力较强的翻译,听、说、读、写成绩按照3∶3∶2∶2的比确定,计算两名应试者的平均成绩(百分制).从他们的成绩看,应该录取谁?
提升练习
解:听、说、读、写的成绩按照3∶3∶2∶2的
比确定,则甲的平均成绩为
85×3+83×3+78×2+75×2
3+3+2+2
=
81,
乙的平均成绩为
73×3+80×3+85×2+82×2
3+3+2+2
=
79.3.
显然甲的成绩比乙的高,所以从成绩看,应该录取甲.
当堂练习
(1)105,103,101,100,114,108,110, 106,98,102;(共10个)
(2)4203,4204,4200,4194,4204,4209, 4195,4199.(共8个)
计算下列两组平均数
拓展练习
解:
(1)将数组中各个数均减去100,得:
5,3,1,0,14,8,10, 6,-2,2
=100+(5+3+1+0+14+8+10+6-2+2)÷10
=100+4.7=104.7
思考:
有没有简便方法计算
(2)将数组中各个数均减去4200,得:
3,4,0,-6,4,9, -5,-1
=4200+(3+4+0-6+4+9-5-1)÷8
=4200+1=4201
若设一组数据x1、x2…….xn的平均数为m
x1+a,x2+a……xn+a的平均数为_____
m+a
1、已知一组数据 的平均数为a,则另一组数据
的平均数是
4a
4a-2
2、已知数据 的平均数为a, 则数据
的平均数为 ; 的平均数为
a+7
3 如果两组数据 和 的平均数分别为a和b,求一组新数据 的平均数.
拓展练习
解:
2.加权平均数的意义
加权平均数反映一组数据中按各数据占有的不同权重时总体的平均大小情况.
3.数据的权的意义
权反映数据的重要程度,数据权的改变一般会影响这组数据的平均水平.
4.加权平均数公式
课堂小结
1、算术平均数反映一组数据的平均水平
数据总和除以数据总个数.
一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分,各项成绩均按百分制,然后再按演讲内容占50%、演讲能力占40%、演讲效果占10%的比例,计算选手的综合成绩(百分制).进入决赛的前两名选手的单项成绩如下表所示:
选手 演讲内容 演讲能力 演讲效果
A 85 95 95
B 95 85 95
请决出两人的名次.
课后练习
解:选手A的最后得分是
85×50%+95×40%+95×10%
50%+40%+10%
=42.5+38+9.5
=90.
选手B的最后得分是
95×50%+85×40%+95×10%
50%+40%+10%
=47.5+34+9.5
=91.
由上可知选手B获得第一名,选手A获得第二名.
选手 演讲内容 (50%) 演讲能力 (40%) 演讲效果
(10%)
A 85 95 95
B 95 85 95
课后练习
第1课时 平均数
一、数据的集中趋势
导入新课
讲授新课
当堂练习
课堂小结
沪科版数学八年级下册
20.2 数据的集中趋势与离散程度
当你听到“小亮的身高在班上是中等偏上的”,“A 篮球队队员比B 队更年轻”等诸如此类的说法时,你思考过这些话的含义吗?你知道人们是如何作出这一判断的吗?
导入新课
数据2、3、4、1、2的平均数是________,这个平均数叫做_________平均数.
2.4
算术
日常生活中,我们常用平均数表示一组数据的“平均水平”
新课导入
样本平均数估计总体平均数
测试 第1次 第2次 第3次 第4次 第5次 第6次 第7次 第8次
小明 10 10 11 10 14 16 16 17
小华 11 12 12 12 14 13 15 13
问题2、小明和小华参加某体育项目的训练,近期的8次测试成绩(单位:分)如表:
若从这选一人参加市中学生运动会,从平均水平的角度考虑你认为选谁去合适
新课导入
问题1、数据2、3、4、1、2的平均数是________,
还记得小学如何计算平均数吗?
2.4
计算两人的平均成绩
(10+10+11+10+14+16+16+17)÷8=13
(11+12+12+12+14+13+15+13)÷8=12.75
从平均水平的角度考虑选小明去较合适
记为 ,读作:“x拔”.
算术平均数
定义:
一般地,对于n个数x1,x2,…,xn,我们 把 (x1+x2+…+xn)叫做这n个数的算术平均数;简称平均数
讲授新课
1、 如图是小丽五次射击成绩的折线图u根据图中信息,小丽这五次成绩的平均数是 环
概念强化
(7+9+8+8+10)÷5=8.4(环)
8.4
2、 为了估计某矿区铁矿石的含铁量,抽取了15块矿石,测得它们的含铁量如下:(单位:%)
26 24 21 28 27 23 23 25
26 22 21 30 26 20 30
则样本的平均数是多少 估计这个矿区铁矿石的平均含铁量约为多少
概念强化
答:估计这个矿区铁矿石的平均含铁量约为24.8%
样本的平均数
样本平均数估计总体平均数
在一次体育课上,体育老师对九年级一班的40名同学进行了立定跳远项目的测试,测试所得分数及相应的人数如图所示.则这次测试的平均分为多少?
新知探究
思考
问题1、完成下表填空
分数 6 8 10
人数
5
15
20
问题2、这样计算平均数合理吗?
(6+8+10)÷3=8(分)
问题3、40名学生测试的总分数应该如何计算?
6×5+8×15+10×20=350
问题4、40名学生测试的平均分数应该如何计算?
加权平均数
在求n个数的算术平均数时,如果x1出现f1次,x2出现f2次,…,xk出现fk次(这里f1+f2+…+fk=n)那么这n个数的算术平均数
也叫做x1,x2,…,xk这k个数的加权平均数,其中f1,f2,…,fk分别叫做x1,x2,…,xk的权。
加权平均数
新知讲解
例1 植树节到了, 某单位组织职工开展植树竞赛, 下图反映的是植树量与人数之间的关系.
3
4
5
6
7
8
棵数
12
10
8
6
4
2
0
人数
0
请根据图中信息计算:
(1)总共有多少人参加了本次活动?
(2)总共植树多少棵?
(3)平均每人植树多少棵?
例题讲授
(3)平均每人植树:155÷32≈4.8 (棵)
解:
(1)参加本次活动的总人数:
1+8+1+10+8+3+1=32(人)
(2)总共植树:3×8+4×1+5×10+6×8+7×3+8×1=155(棵).
0
2
4
6
8
10
12
14
40
50
60
70
80
90
频数
周长/cm
例1、为了绿化环境,柳荫街引进一批法国梧桐,三年后这些树的树干的周长情况如图所示
答:这批梧桐树干的平均周长是63.8cm
(1)总共有多少棵树?
(2)这批法国梧桐树干的平均周长是多少?(精确到0.1cm)(可以使用计算器)
解:
例题讲授
(1)法国梧桐的总数:
8+12+14+10+6=50(棵)
(2)
某校拟招聘一名优秀数学教师,现有甲、乙、丙三名教师入围,三名教师笔试、面试成绩如下表所示.综合成绩按照笔试占60%、面试占40%进行计算,学校录取综合成绩得分最高者,则被录取教师的综合成绩为________分.
78.8
【解析】 :甲的综合成绩为80×60%+76×40%=78.4(分),乙的综合成绩为82×60%+74×40%=78.8(分),
丙的综合成绩为78×60%+78×40%=78(分),
其中78.8>78.4>78,乙的综合成绩最高,
∴被录取的教师为乙,其综合成绩为78.8分,
故答案为:78.8
测试选手 测试成绩
创新 唱功 综合知识
甲 72 85 67
乙 85 74 70
∴按三项平均值取第一名选手乙为第一名
解:(1)
某次歌唱比赛,两名选手的成绩如下:
讲授新课
(1)甲、乙三项平均值谁高 若按三项平均值取第一名,则谁是第一名?
(3)若三项测试得分按3:6:1的比例确定个人的测试成绩,此时第一名是谁?
(2)这样确定第一名的方法科学吗
>
(2)不科学,因为创新、唱功、综合知识这三项在表现选手综合水平里所占的重要性不一样
讨论
(3)
此时第一名是选手甲
概念二:
一般地,若n个数x1,x2,…,xn的权分别 是w1,w2,…,wn ,则这n个数
据的加权平均数为
=
讲授新课
在实际问题中,一组数据里的各个数据的“重要程度” 未必相同.因而,在计算这组数据的平均数时,往往给每个数据一个“权”.
加权平均数
根据实际需要对不同类型的数据赋予与其重要程度相应的比例,称为这组数据的权.
权
权重的意义:
加权平均数的意义:
各个数据在该组数据中所占有的不同重要性的反映.
按各个数据的权重来反映该组数据的总体平均大小情况.
例题讲授
例2、某校拟招聘一名优秀数学教师,现有甲、乙、丙三名教师入围,三名教师笔试、面试成绩如下表所示.综合成绩按照笔试占60%、面试占40%进行计算,学校录取综合成绩得分最高者,则被录取教师的综合成绩为多少分.
权
教师 成绩(分) 甲 乙 丙
笔试 80 82 78
面试 76 74 78
∵78.8>78.4>78,
乙的综合成绩最高,
∴被录取的教师为乙,其综合成绩为78.8分,
解:
甲的综合成绩:
乙的综合成绩:
丙的综合成绩:
概念总结
1、加权平均数就是把数据按照合理的比例来计算。
2.“权”就是“权重”、“比重”的意思
3. 加权平均数=数与该数权的积的和÷权之和
4. “权”的常见形式
(1)数据的形式:如50、45、55
(2)比的形式:如3:3:2:2
(3)百分比的形式:如50%、40%、10%
加权平均数
1. 平均数计算:
算术平均数=各数据的和÷数据的个数
2. 平均数的意义:
算术平均数反映一组数据总体的平均大小情况.
加权平均数反映一组数据中按各数据占有的不同权重时总体的平均大小情况.
3. 区别:
加权平均数=(各数据×该数据的权重)的和÷总权数
算术平均数中各数据都是同等的重要, 没有相互间差异;
加权平均数中各数据都有各自不同的权重地位,彼此之间存在差异性的区别.
算术平均数与加权平均数的比较
概念总结
考试 测试1 测试2 测试3 期中 期末
成绩 89 78 85 90 87
例3、 小青在七年级第二学期的数学成绩如下表格, 请按图示的测试、期中、期末的权重, 计算小青同学该学期总评成绩
期中
30%
期末
60%
平时
10%
解:
先计算小青的平时成绩:
(89+78+85)÷3
= 84
再计算小青的总评成绩:
84×10%+ 90×30%+ 87×60%
= 87.6 (分)
例题讲授
1、某校生物兴趣小组11人到校外采集植物标本,其中2人每人采集到6件,4人每人采集到3件,5人每人采集到4件,则这个兴趣小组平均每人采集标本( )
A、3件 B、4件 C、5件 D、6件
2、10名学生的平均成绩是x,如果另外5名学生
平均成绩得84分,那么这15人的平均成绩是( )
A、 B、
C、 D、
B
B
课堂练习
3.李大伯有一片果林,共有80棵果树.某日,李大伯开始采摘今年第一批成熟的果子,他随机选取2棵果树共摘得10个果子,质量分别为(单位:㎏):0.28,0.26,0.24,0.23,0.25,0.24,0.26,0.26,0.25,0.23.以此估算,李大伯收获的这批果子的单个质量和总质量分别约为( )
A.0.25 ㎏,200 ㎏ B.2.5 ㎏,100 ㎏
C.0.25 ㎏,100 ㎏ D.2.5 ㎏,200 ㎏
C
课堂练习
4、某商场用加权平均数来确定什锦糖的单价,由单价为15元/千克的甲种糖果10千克,单价为12元/千克的乙种糖果20千克,单价为10元/千克的丙种糖果30千克混合成的什锦糖果的单价应定为( )
(A)11元/千克 (B)11.5元/千克
(C)12元/千克 (D)12.5元/千克
B
5、某商场6月份随机调查了6天的营业额,结果分别如下(单位:万元):2.8,3.2,3.4,3.0,3.1,3.7,试估算该商场6月份的总营业额大约是( )
(A)84万元 (B)96万元 (C)93万元 (D)111万元
B
由此可估计该商场6月份总营业额大约是3.2×30=96(万元)
=3.2(万元)
课堂练习
6、有五盒火柴,每盒火柴的根数如下:71 、73、 76、 77 、78
则每盒火柴的平均根数是___.
7、5个数据的和为405,其中一个数据为85,那么另4个数据的平均数是 _.
8、小明来学校的路程是100米,速度是5米/秒,回家的路程是100米,速度是2.5米/秒,在整个过程中的平均速度是:_____
课堂练习
75
80
200÷(100÷5+100÷2.5)=(米/秒)
总路程÷总时间=平均速度
9、老师对同学们每学期总评成绩时,并不是简单地将一个学生的平时成绩与考试成绩相加除以2而是按照“平时练习占 40%, 考试成绩占60% ”的比例计算,其中考试成绩更为重要.这样,如果一个学生的平时成绩为70分,考试成绩为90分,那么他的学期总评成绩就应该为多少呢?
课堂练习
解:
该同学的学期总评成绩是:
70×30%+90×60%
=82(分)
年龄/岁 13 14 15 16
频数 1 4 5 2
求校女子排球队队员的平均年龄(结果取整数).
解:
答:校女子排球队队员的平均年龄为15岁
10、下表是校女子排球队队员的年龄分布.
课堂练习
1、某次舞蹈大赛的记分规则为:从七位评委的打分中去掉一个最高分和一个最低分后计算平均分作为最后得分.以下是在该次比赛中七位评委对小菲与小岚的打分情况(单位:分):
提升练习
请通过计算说明谁的最后得分高.
小菲 80 77 82 83 75 78 89
小岚 79 80 77 76 82 85 81
解:小菲去掉一个最高分89分,去掉一个最低分75分,最后得分为
小岚去掉一个最高分85分,去掉一个最低分76分,最后得分为
∵80分>79.8分,∴小菲的最后得分高
2、一家公司打算招聘一名英文翻译,对甲、乙两名应试者进行了听、说、读、写的英语水平测试,他们各项的成绩(百分制)如下:
应试者 听 说 读 写
甲 85 83 78 75
乙 73 80 85 82
如果这家公司想招一名口语能力较强的翻译,听、说、读、写成绩按照3∶3∶2∶2的比确定,计算两名应试者的平均成绩(百分制).从他们的成绩看,应该录取谁?
提升练习
解:听、说、读、写的成绩按照3∶3∶2∶2的
比确定,则甲的平均成绩为
85×3+83×3+78×2+75×2
3+3+2+2
=
81,
乙的平均成绩为
73×3+80×3+85×2+82×2
3+3+2+2
=
79.3.
显然甲的成绩比乙的高,所以从成绩看,应该录取甲.
当堂练习
(1)105,103,101,100,114,108,110, 106,98,102;(共10个)
(2)4203,4204,4200,4194,4204,4209, 4195,4199.(共8个)
计算下列两组平均数
拓展练习
解:
(1)将数组中各个数均减去100,得:
5,3,1,0,14,8,10, 6,-2,2
=100+(5+3+1+0+14+8+10+6-2+2)÷10
=100+4.7=104.7
思考:
有没有简便方法计算
(2)将数组中各个数均减去4200,得:
3,4,0,-6,4,9, -5,-1
=4200+(3+4+0-6+4+9-5-1)÷8
=4200+1=4201
若设一组数据x1、x2…….xn的平均数为m
x1+a,x2+a……xn+a的平均数为_____
m+a
1、已知一组数据 的平均数为a,则另一组数据
的平均数是
4a
4a-2
2、已知数据 的平均数为a, 则数据
的平均数为 ; 的平均数为
a+7
3 如果两组数据 和 的平均数分别为a和b,求一组新数据 的平均数.
拓展练习
解:
2.加权平均数的意义
加权平均数反映一组数据中按各数据占有的不同权重时总体的平均大小情况.
3.数据的权的意义
权反映数据的重要程度,数据权的改变一般会影响这组数据的平均水平.
4.加权平均数公式
课堂小结
1、算术平均数反映一组数据的平均水平
数据总和除以数据总个数.
一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分,各项成绩均按百分制,然后再按演讲内容占50%、演讲能力占40%、演讲效果占10%的比例,计算选手的综合成绩(百分制).进入决赛的前两名选手的单项成绩如下表所示:
选手 演讲内容 演讲能力 演讲效果
A 85 95 95
B 95 85 95
请决出两人的名次.
课后练习
解:选手A的最后得分是
85×50%+95×40%+95×10%
50%+40%+10%
=42.5+38+9.5
=90.
选手B的最后得分是
95×50%+85×40%+95×10%
50%+40%+10%
=47.5+34+9.5
=91.
由上可知选手B获得第一名,选手A获得第二名.
选手 演讲内容 (50%) 演讲能力 (40%) 演讲效果
(10%)
A 85 95 95
B 95 85 95
课后练习
