六年级下册数学 6.4数学思考 课件(17张PPT)
文档属性
| 名称 | 六年级下册数学 6.4数学思考 课件(17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 21.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-18 12:34:52 | ||
图片预览





文档简介
(共17张PPT)
数学思考
知识梳理
能运用一定的规律解决较复杂的数学问题。
合作探究,分享方法
预设1:
引入情境,探究规律
唉,画乱了,也数不清多少条线段了。
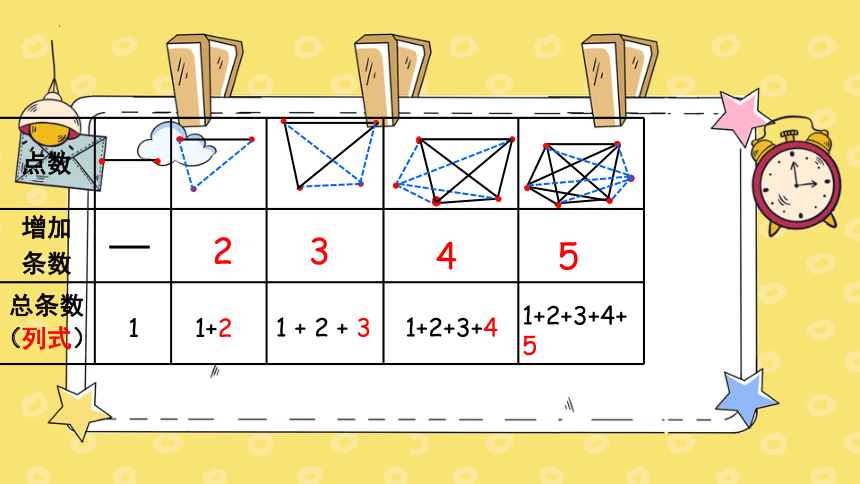
点数
增加 条数
总条数 (列式)
1
1+2
2
1 + 2 + 3
3
1+2+3+4
4
1+2+3+4+5
5
观察、分析下面各列数的变化规律,在括号里填上适当的数。[★★]
(1)1 4 9 16 ( ) ( ) ( )
(2)2 3 6 18 ( ) ( ) 209952
(3)1 8 27 ( ) ( ) ( ) 343
(4)3 1 6 2 12 4 ( ) ( ) ( )
(5) ( ) ( ) ( )
25
36
49
108
1944
23
33
43
53
63
73
64
125
216
13
3位同学,相互握手一次,一共要握多少次?(4位,5位呢?)
要求:以小组为单位完成探索卡,先想一想怎样握手比较有规律?1人连线,1人填表格,2人出主意,检查。
巩固拓展
用数字“1” 表示到会,用数字“0”表示没到会。
A B C D E F
第一次 1 1 1 0 0 0
第二次 0 1 0 1 1 0
第三次 1 0 0 0 1 1
16×15=240(场)
中超有广州恒大,上海申花,重庆力帆,杭州绿城,北京国安,辽宁宏运,山东鲁能等16支球队。
①如果这16只足球队进行单循环赛(也就是说每两支球队之间只进行一场比赛),共有多少场比赛?
答:略。
15+14+13+…+1=120(场)
②如果是双循环赛共有几场比赛?(理解双循环意思)
一个学生做了好事,老师调查是谁做的好事。甲说:“是乙做的。”乙说 “是丁做的。”丙说:“不是我做的。”丁说:“乙在说谎。”已知这四个人中只有一个人说了实话。那么,说实话的是( ),做好事的是( )。
A.甲 B.乙 C.丙 D.丁
甲
乙
丙
丁
甲
乙
丙
丁
甲
乙
丙
丁
甲
乙
丙
丁
D
C
多边形
边 数
3
4
5
6
内角和
180°
540°
720°
(1)多边形内角和与它的边数有什么关系?
(2)一个九边形的内角和是多少度?
多边形内角和=(边数-2)×180°
(9-2)×180°=1260°
360°
巩固拓展
(2)你能推出∠1=∠3吗?
那接下来怎么办呢?
把∠1和∠2, ∠2和∠3的关系用等式表示出来。
根据第(1)题的结论,可以得到∠1+∠2=180°,∠2+∠3=180°。
根据等式的性质,等式的两边都减去∠2,可以得到∠1=180°-
∠2°,∠3=180-∠2°。
因为180-∠2°=180-∠2°。所以∠1=∠3。
问题:1. 第7幅图每行有几个棋子?有几行?共有几个棋子?
3. 第15幅图共有几个棋子?
巩固练习,提升认识
7×7=49(个)
15×15=225(个)
观察下图,想一想。
(1)第7幅图有多少个棋子?第15幅图呢?
2. 每边的棋子数与图形的序号有什么关系?
如图,在三角形ABC中,线段BO和CO分别将∠ABC和∠ACB平均分成了两份。[★★★★]
(2)如果∠A=70°,则∠O是多少度?
引入情境,探究新知
出示信息,明确问题
问题:你想怎样解决这个问题?动手试一试吧。
六年级有三个班,每班有2个班长。开班长会时,每次每班只要一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、F。请问:哪两位班长是同班的?
如图,仔细观察,你可以发现一条规律。[★★★★★]
(2)运用这条规律计算:
20232 - 20222 + 20212 - 20202 + … + 32 - 22 + 12
同学们再见
数学思考
知识梳理
能运用一定的规律解决较复杂的数学问题。
合作探究,分享方法
预设1:
引入情境,探究规律
唉,画乱了,也数不清多少条线段了。
点数
增加 条数
总条数 (列式)
1
1+2
2
1 + 2 + 3
3
1+2+3+4
4
1+2+3+4+5
5
观察、分析下面各列数的变化规律,在括号里填上适当的数。[★★]
(1)1 4 9 16 ( ) ( ) ( )
(2)2 3 6 18 ( ) ( ) 209952
(3)1 8 27 ( ) ( ) ( ) 343
(4)3 1 6 2 12 4 ( ) ( ) ( )
(5) ( ) ( ) ( )
25
36
49
108
1944
23
33
43
53
63
73
64
125
216
13
3位同学,相互握手一次,一共要握多少次?(4位,5位呢?)
要求:以小组为单位完成探索卡,先想一想怎样握手比较有规律?1人连线,1人填表格,2人出主意,检查。
巩固拓展
用数字“1” 表示到会,用数字“0”表示没到会。
A B C D E F
第一次 1 1 1 0 0 0
第二次 0 1 0 1 1 0
第三次 1 0 0 0 1 1
16×15=240(场)
中超有广州恒大,上海申花,重庆力帆,杭州绿城,北京国安,辽宁宏运,山东鲁能等16支球队。
①如果这16只足球队进行单循环赛(也就是说每两支球队之间只进行一场比赛),共有多少场比赛?
答:略。
15+14+13+…+1=120(场)
②如果是双循环赛共有几场比赛?(理解双循环意思)
一个学生做了好事,老师调查是谁做的好事。甲说:“是乙做的。”乙说 “是丁做的。”丙说:“不是我做的。”丁说:“乙在说谎。”已知这四个人中只有一个人说了实话。那么,说实话的是( ),做好事的是( )。
A.甲 B.乙 C.丙 D.丁
甲
乙
丙
丁
甲
乙
丙
丁
甲
乙
丙
丁
甲
乙
丙
丁
D
C
多边形
边 数
3
4
5
6
内角和
180°
540°
720°
(1)多边形内角和与它的边数有什么关系?
(2)一个九边形的内角和是多少度?
多边形内角和=(边数-2)×180°
(9-2)×180°=1260°
360°
巩固拓展
(2)你能推出∠1=∠3吗?
那接下来怎么办呢?
把∠1和∠2, ∠2和∠3的关系用等式表示出来。
根据第(1)题的结论,可以得到∠1+∠2=180°,∠2+∠3=180°。
根据等式的性质,等式的两边都减去∠2,可以得到∠1=180°-
∠2°,∠3=180-∠2°。
因为180-∠2°=180-∠2°。所以∠1=∠3。
问题:1. 第7幅图每行有几个棋子?有几行?共有几个棋子?
3. 第15幅图共有几个棋子?
巩固练习,提升认识
7×7=49(个)
15×15=225(个)
观察下图,想一想。
(1)第7幅图有多少个棋子?第15幅图呢?
2. 每边的棋子数与图形的序号有什么关系?
如图,在三角形ABC中,线段BO和CO分别将∠ABC和∠ACB平均分成了两份。[★★★★]
(2)如果∠A=70°,则∠O是多少度?
引入情境,探究新知
出示信息,明确问题
问题:你想怎样解决这个问题?动手试一试吧。
六年级有三个班,每班有2个班长。开班长会时,每次每班只要一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、F。请问:哪两位班长是同班的?
如图,仔细观察,你可以发现一条规律。[★★★★★]
(2)运用这条规律计算:
20232 - 20222 + 20212 - 20202 + … + 32 - 22 + 12
同学们再见
