人教版六年级下学期数学6.1.2数的运算课件(共21张PPT)
文档属性
| 名称 | 人教版六年级下学期数学6.1.2数的运算课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 21.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-18 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
数的运算
进一步理解并掌握数的估算的方法及它们之间的关系。
掌握数的估算方法,能选择合理的方法解决实际问题。
数的运算
加减法
都是把相同计数单位的数相加减。
乘除法
小数乘除法把除数转化成整数再计算。分数除法要转化成分数乘法计算。
整数、小数、分数四则运算的相同点
新课讲解
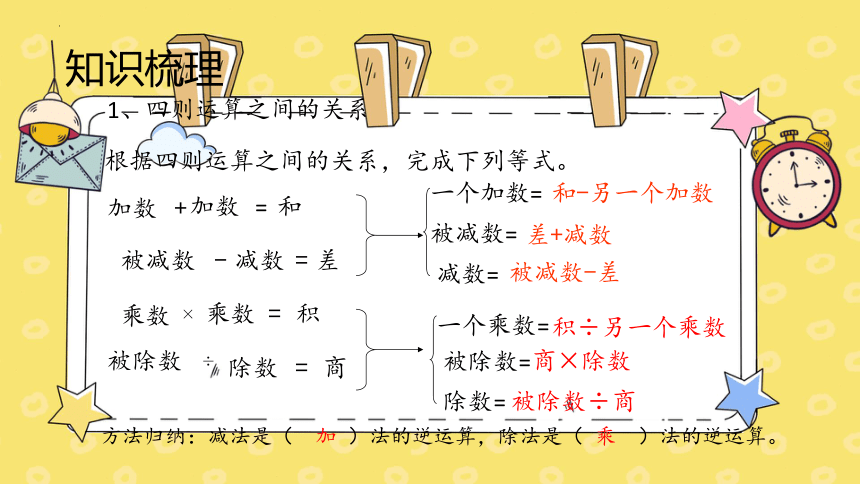
根据四则运算之间的关系,完成下列等式。
和-另一个加数
1、四则运算之间的关系
+
=
加数
加数
和
被减数
减数
差
乘数
乘数
积
-
=
×
=
被除数
除数
÷
商
=
一个加数=
被减数=
减数=
一个乘数=
被除数=
除数=
差+减数
被减数-差
积÷另一个乘数
商×除数
被除数÷商
方法归纳:减法是( 加 )法的逆运算,除法是( 乘 )法的逆运算。
知识梳理
计算法则。
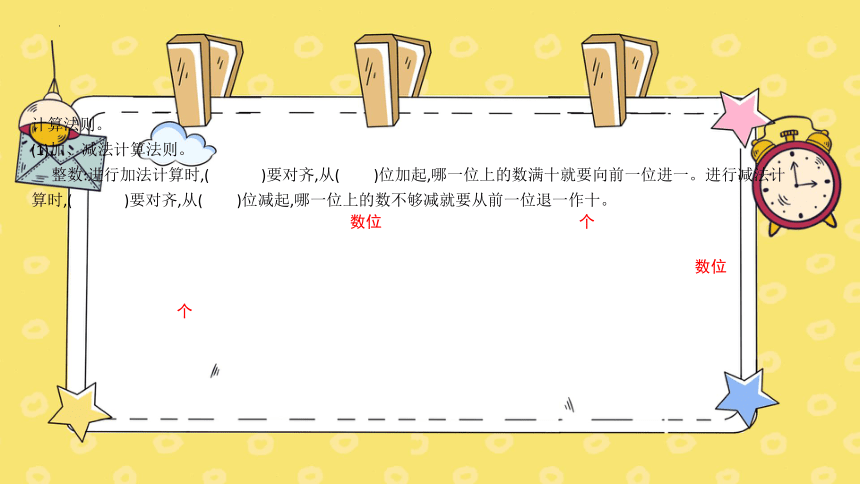
(1)加、减法计算法则。
整数:进行加法计算时,( )要对齐,从( )位加起,哪一位上的数满十就要向前一位进一。进行减法计算时,( )要对齐,从( )位减起,哪一位上的数不够减就要从前一位退一作十。
个
数位
个
数位
整数:从低位到高位,分别用一个因数的每一位上的数去乘另一个因数,用一个因数的哪一位上的数去乘所得的积的末位就要和那一位对齐,然后把几次乘得的积相加。
小数:先按整数乘法计算出积,再看因数中一共有几位小数。就从积的右边起数出几位,点上小数点;当位数不够时,用0补足。
分数:用分子相乘的积作分子,分母相乘的积作分母,能约分的先约分,再相乘。
乘法
1、6.99×8.99与63比,哪个大?
只需要比较大小,不需要计算出准确的值,把6.99和8.99都往大了估,计算出的结果大于实际的积。
6.99≈7,8.99≈9
7×9=63
6.99×8.99<63
解决问题2
学生夏令营组织远足,原计划3小时走完11.25km。实际2.5小时就走完了原定路程。实际比原计划每小时多走多少千米?
11.25÷2.5-11.25÷3=0.75(千米)
答:实际比原计划每小时多走0.75千米。
难点突破
四则混合运算的顺序。
(1)算式如果只有加、减法或只有乘除法,要从( )往( )依次计算。
(2)算式如果有加、减、乘、除法的,要先算( )法,后算
( )法。
(3)算式如果有括号,要先算小括号里的数,再算中括号里的数。
加减
乘除
右
左
如果有括号,先算括号里面的。
2.数的运算顺序
举手回答:四则混合运算的计算顺序是怎样的?
如果是同一级运算,一般按从左往右的顺序依次进行计算。
如果既有加减、又有乘除法,先算乘除法、再算加减。
新课讲解
125×8=100
1000÷125=8
1000÷8=125
2.5×4=10
10÷2.5=4
10÷4=2.5
积÷因数=另一个因数
因数×因数=积
被除数÷除数=商
被除数÷商=除数
商×除数=被除数
观察下列算式,说一说四则运算之间的关系。
1、学校食堂计划购买1500千克大米。
(2)如果够了,还剩下多少千克?如果不够,还需要购进多少千克?
需要精确计算
先求半个月需要多少千克大米:
95×(30÷2)=1425(千克)
再求还剩下多少千克:
1500-1425=75(千克)
答:还剩下75千克。
估算
203÷50≈ 19×31 ≈ 405+398 ≈
101×49 ≈ 4190÷69≈ 8201-199 ≈
4
600
800
5000
60
8000
巩固练习
解方程或解比例。
7x-2.1=6.9
解:7x=6.9+2.1
7x=9
x=9÷7
0.9:x=9:0.7
解:9x=0.9×0.7
9x=0.63
x=0.63÷9
x=0.07
5.3×74=392.2
420+38=458
根据已知算式写两道逆运算算式。
392.2÷74=5.3
392.2÷5.3=74
458-420=38
458-38=420
课堂练习
一个加数不变,另一个加数增加或减少一个数,和也增加或减少同一个数。
一个加数增加一个数,另一个加数减少同一个数,和不变。
和的变化规律
减数不变,被减数增加或减少一个数,差也增加或减少同一个数。
被减数不变,减数增加或减少一个数,差减少或增加同一个数。
差的变化规律
被减数和减数都增加或减少同一个数,差不变。
估算下面各题。
421×98 ≈ 810×48 ≈ 809×38 ≈
79×22 ≈ 213×92 ≈ 502×78 ≈
1600
40000
32000
42000
20000
40000
845÷65=139(组)
答:一共设了13个服务站。
组委会在长达845米的山路中每隔65米设置一个服务站(起点不设)。一共设了多少个服务站?
巩固练习
课后作业
1、从教材课后习题中选取2、从课时练中选取
同学们再见
数的运算
进一步理解并掌握数的估算的方法及它们之间的关系。
掌握数的估算方法,能选择合理的方法解决实际问题。
数的运算
加减法
都是把相同计数单位的数相加减。
乘除法
小数乘除法把除数转化成整数再计算。分数除法要转化成分数乘法计算。
整数、小数、分数四则运算的相同点
新课讲解
根据四则运算之间的关系,完成下列等式。
和-另一个加数
1、四则运算之间的关系
+
=
加数
加数
和
被减数
减数
差
乘数
乘数
积
-
=
×
=
被除数
除数
÷
商
=
一个加数=
被减数=
减数=
一个乘数=
被除数=
除数=
差+减数
被减数-差
积÷另一个乘数
商×除数
被除数÷商
方法归纳:减法是( 加 )法的逆运算,除法是( 乘 )法的逆运算。
知识梳理
计算法则。
(1)加、减法计算法则。
整数:进行加法计算时,( )要对齐,从( )位加起,哪一位上的数满十就要向前一位进一。进行减法计算时,( )要对齐,从( )位减起,哪一位上的数不够减就要从前一位退一作十。
个
数位
个
数位
整数:从低位到高位,分别用一个因数的每一位上的数去乘另一个因数,用一个因数的哪一位上的数去乘所得的积的末位就要和那一位对齐,然后把几次乘得的积相加。
小数:先按整数乘法计算出积,再看因数中一共有几位小数。就从积的右边起数出几位,点上小数点;当位数不够时,用0补足。
分数:用分子相乘的积作分子,分母相乘的积作分母,能约分的先约分,再相乘。
乘法
1、6.99×8.99与63比,哪个大?
只需要比较大小,不需要计算出准确的值,把6.99和8.99都往大了估,计算出的结果大于实际的积。
6.99≈7,8.99≈9
7×9=63
6.99×8.99<63
解决问题2
学生夏令营组织远足,原计划3小时走完11.25km。实际2.5小时就走完了原定路程。实际比原计划每小时多走多少千米?
11.25÷2.5-11.25÷3=0.75(千米)
答:实际比原计划每小时多走0.75千米。
难点突破
四则混合运算的顺序。
(1)算式如果只有加、减法或只有乘除法,要从( )往( )依次计算。
(2)算式如果有加、减、乘、除法的,要先算( )法,后算
( )法。
(3)算式如果有括号,要先算小括号里的数,再算中括号里的数。
加减
乘除
右
左
如果有括号,先算括号里面的。
2.数的运算顺序
举手回答:四则混合运算的计算顺序是怎样的?
如果是同一级运算,一般按从左往右的顺序依次进行计算。
如果既有加减、又有乘除法,先算乘除法、再算加减。
新课讲解
125×8=100
1000÷125=8
1000÷8=125
2.5×4=10
10÷2.5=4
10÷4=2.5
积÷因数=另一个因数
因数×因数=积
被除数÷除数=商
被除数÷商=除数
商×除数=被除数
观察下列算式,说一说四则运算之间的关系。
1、学校食堂计划购买1500千克大米。
(2)如果够了,还剩下多少千克?如果不够,还需要购进多少千克?
需要精确计算
先求半个月需要多少千克大米:
95×(30÷2)=1425(千克)
再求还剩下多少千克:
1500-1425=75(千克)
答:还剩下75千克。
估算
203÷50≈ 19×31 ≈ 405+398 ≈
101×49 ≈ 4190÷69≈ 8201-199 ≈
4
600
800
5000
60
8000
巩固练习
解方程或解比例。
7x-2.1=6.9
解:7x=6.9+2.1
7x=9
x=9÷7
0.9:x=9:0.7
解:9x=0.9×0.7
9x=0.63
x=0.63÷9
x=0.07
5.3×74=392.2
420+38=458
根据已知算式写两道逆运算算式。
392.2÷74=5.3
392.2÷5.3=74
458-420=38
458-38=420
课堂练习
一个加数不变,另一个加数增加或减少一个数,和也增加或减少同一个数。
一个加数增加一个数,另一个加数减少同一个数,和不变。
和的变化规律
减数不变,被减数增加或减少一个数,差也增加或减少同一个数。
被减数不变,减数增加或减少一个数,差减少或增加同一个数。
差的变化规律
被减数和减数都增加或减少同一个数,差不变。
估算下面各题。
421×98 ≈ 810×48 ≈ 809×38 ≈
79×22 ≈ 213×92 ≈ 502×78 ≈
1600
40000
32000
42000
20000
40000
845÷65=139(组)
答:一共设了13个服务站。
组委会在长达845米的山路中每隔65米设置一个服务站(起点不设)。一共设了多少个服务站?
巩固练习
课后作业
1、从教材课后习题中选取2、从课时练中选取
同学们再见
