人教版六年级下学期数学第六单元6.4数学思考课件(共17张PPT)
文档属性
| 名称 | 人教版六年级下学期数学第六单元6.4数学思考课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 33.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-18 13:38:15 | ||
图片预览





文档简介
(共17张PPT)
数学思考
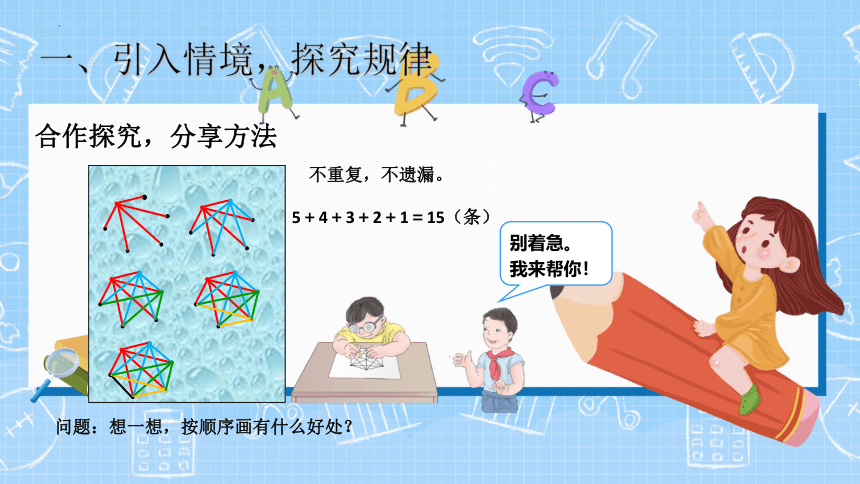
不重复,不遗漏。
问题:想一想,按顺序画有什么好处?
预设2:
5+4+3+2+1=15(条)
合作探究,分享方法
一、引入情境,探究规律
别着急。
我来帮你!
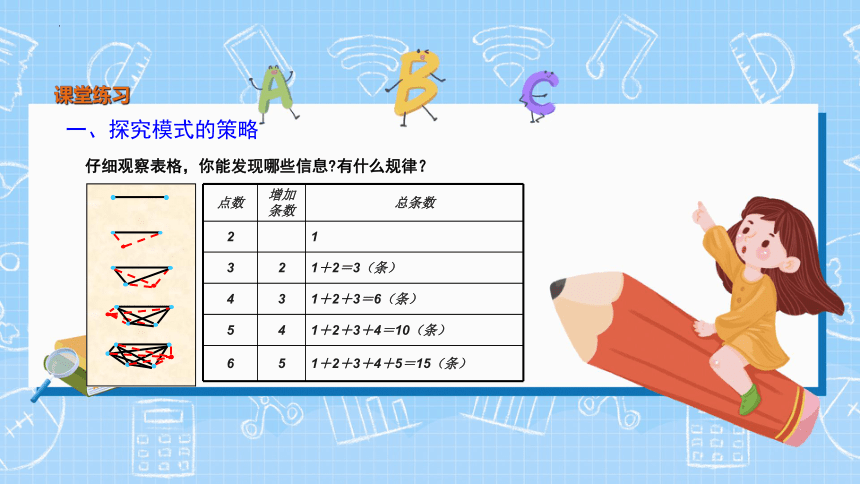
课堂练习
仔细观察表格,你能发现哪些信息 有什么规律?
点数 增加条数 总条数
2 1
3 2 1+2=3(条)
4 3 1+2+3=6(条)
5 4 1+2+3+4=10(条)
6 5 1+2+3+4+5=15(条)
一、探究模式的策略
100
n
99
n-1
1+2+3+…+99
1+2+3+…+(n-1)
8
20
7
19
1+2+3+…+7
1+2+3+…+19
观察、分析下面各列数的变化规律,在括号里填上适当的数。[★★]
(1)1 4 9 16 ( ) ( ) ( )
(2)2 3 6 18 ( ) ( ) 209952
(3)1 8 27 ( ) ( ) ( ) 343
(4)3 1 6 2 12 4 ( ) ( ) ( )
(5) ( ) ( ) ( )
25
36
49
108
1944
64
125
216
×2
×2
×2
24
×2
48
×2
×2
×2
8
任意的8个点,将它们每两点连成一条线,能连成多少条线段 (你能借鉴握手中的数学问题解决吗?)
巩固拓展
A B C D E F
第一次 1 1 1 0 0 0
第二次 0 1 0 1 1 0
第三次 1 0 0 0 1 1
A B C D E F
第一次 1 1 1 0 0 0
第二次 0 1 0 1 1 0
第三次 1 0 0 0 1 1
问题:1. A可能和谁是同班?
2. 请你根据表格继续推理,B、C可能和谁是同班呢?
A B C D E F
第一次 1 1 1 0 0 0
第二次 0 1 0 1 1 0
第三次 1 0 0 0 1 1
A B C D E F
第一次 1 1 1 0 0 0
第二次 0 1 0 1 1 0
第三次 1 0 0 0 1 1
√ √
√ √ √
√ √
×
√ √ √
√ √ √
×
√ ×
1+2+3+4+5+6+7
问题:1. 按照规律,8个点能连几条线段?
2. 为什么有8个点,列式却依次加到7呢?
合作探究,分享方法
一、引入情境,探究规律
3. 想一想,能用简单方法计算吗?
=(1+7)+(2+6)+(3+5)+4
=28(条) ——8个点
=8×3+4
(4)观察下面一排圆柱,分析它们的底面直径和高的变化引起体积变化的规律。根据这个规律,用含有字母的式子表示第n个圆柱的体积是( )。
A.πn B.πn2 C.πn3 D.4πn2
圆柱的体积=底面积×高
=πr2h
π
C
数学思考数学思考
把一个长方形看作一个整体,一条直线可以把它分成2部分,2条直线可以把它分成4部分,3条直线最多可以把它分成7部分……那么100条直线最多可以把这个长方形分成多少个部分呢?
课堂小结
我的收获
遇到复杂的问题,可以尝试从简单问题去思考,逐步找到其中的规律,从而解决复杂的问题。
列表也是解决复杂问题的好方法。
观察下图,想一想。
(2)第n幅图有多少个棋子?
问题:第n幅图每边有多少个棋子?一共有多少个棋子?
巩固练习,提升认识
每行的棋子数×行数=棋子总数
n × n = 棋子总数
n2 =棋子总数
小红用大小相同的黑白方块按照下图这样拼图,先观察图形并填表,再回答问题。[★★★★]
图序 1 2 3 ···
图中黑方块的个数 ···
4
6
8
2n+2
引入情境,探究新知
解决问题,分享方法
用数字“1” 表示到会,用数字“0”表示没到会。
A B C D E F
第一次 1 1 1 0 0 0
第二次 0 1 0 1 1 0
第三次 1 0 0 0 1 1
用列表的方法试一试!
聪明出于勤奋,天才在于积累。
数学思考
不重复,不遗漏。
问题:想一想,按顺序画有什么好处?
预设2:
5+4+3+2+1=15(条)
合作探究,分享方法
一、引入情境,探究规律
别着急。
我来帮你!
课堂练习
仔细观察表格,你能发现哪些信息 有什么规律?
点数 增加条数 总条数
2 1
3 2 1+2=3(条)
4 3 1+2+3=6(条)
5 4 1+2+3+4=10(条)
6 5 1+2+3+4+5=15(条)
一、探究模式的策略
100
n
99
n-1
1+2+3+…+99
1+2+3+…+(n-1)
8
20
7
19
1+2+3+…+7
1+2+3+…+19
观察、分析下面各列数的变化规律,在括号里填上适当的数。[★★]
(1)1 4 9 16 ( ) ( ) ( )
(2)2 3 6 18 ( ) ( ) 209952
(3)1 8 27 ( ) ( ) ( ) 343
(4)3 1 6 2 12 4 ( ) ( ) ( )
(5) ( ) ( ) ( )
25
36
49
108
1944
64
125
216
×2
×2
×2
24
×2
48
×2
×2
×2
8
任意的8个点,将它们每两点连成一条线,能连成多少条线段 (你能借鉴握手中的数学问题解决吗?)
巩固拓展
A B C D E F
第一次 1 1 1 0 0 0
第二次 0 1 0 1 1 0
第三次 1 0 0 0 1 1
A B C D E F
第一次 1 1 1 0 0 0
第二次 0 1 0 1 1 0
第三次 1 0 0 0 1 1
问题:1. A可能和谁是同班?
2. 请你根据表格继续推理,B、C可能和谁是同班呢?
A B C D E F
第一次 1 1 1 0 0 0
第二次 0 1 0 1 1 0
第三次 1 0 0 0 1 1
A B C D E F
第一次 1 1 1 0 0 0
第二次 0 1 0 1 1 0
第三次 1 0 0 0 1 1
√ √
√ √ √
√ √
×
√ √ √
√ √ √
×
√ ×
1+2+3+4+5+6+7
问题:1. 按照规律,8个点能连几条线段?
2. 为什么有8个点,列式却依次加到7呢?
合作探究,分享方法
一、引入情境,探究规律
3. 想一想,能用简单方法计算吗?
=(1+7)+(2+6)+(3+5)+4
=28(条) ——8个点
=8×3+4
(4)观察下面一排圆柱,分析它们的底面直径和高的变化引起体积变化的规律。根据这个规律,用含有字母的式子表示第n个圆柱的体积是( )。
A.πn B.πn2 C.πn3 D.4πn2
圆柱的体积=底面积×高
=πr2h
π
C
数学思考数学思考
把一个长方形看作一个整体,一条直线可以把它分成2部分,2条直线可以把它分成4部分,3条直线最多可以把它分成7部分……那么100条直线最多可以把这个长方形分成多少个部分呢?
课堂小结
我的收获
遇到复杂的问题,可以尝试从简单问题去思考,逐步找到其中的规律,从而解决复杂的问题。
列表也是解决复杂问题的好方法。
观察下图,想一想。
(2)第n幅图有多少个棋子?
问题:第n幅图每边有多少个棋子?一共有多少个棋子?
巩固练习,提升认识
每行的棋子数×行数=棋子总数
n × n = 棋子总数
n2 =棋子总数
小红用大小相同的黑白方块按照下图这样拼图,先观察图形并填表,再回答问题。[★★★★]
图序 1 2 3 ···
图中黑方块的个数 ···
4
6
8
2n+2
引入情境,探究新知
解决问题,分享方法
用数字“1” 表示到会,用数字“0”表示没到会。
A B C D E F
第一次 1 1 1 0 0 0
第二次 0 1 0 1 1 0
第三次 1 0 0 0 1 1
用列表的方法试一试!
聪明出于勤奋,天才在于积累。
